Corso di Relativit Generale I Parte Fondamenti di



























































- Slides: 82

Corso di Relatività Generale I Parte Fondamenti di Geometria Differenziale e Relatività Generale

Summary of Riemanian Geometry and Vielbein formulation Manifolds

Introduction to manifolds

Privileged observers and affine manifolds Both Newtonian Physics and Special Relativity have privileged observers Affine Manifold

Affine Manifolds

Curved Manifolds and Atlases The intuitive idea of an atlas of open charts, suitably reformulated in mathematical terms, provides the very definition of a differentiable manifold

Homeomorphisms

Topology invariant under homeomorphisms

Homeomorphic spaces

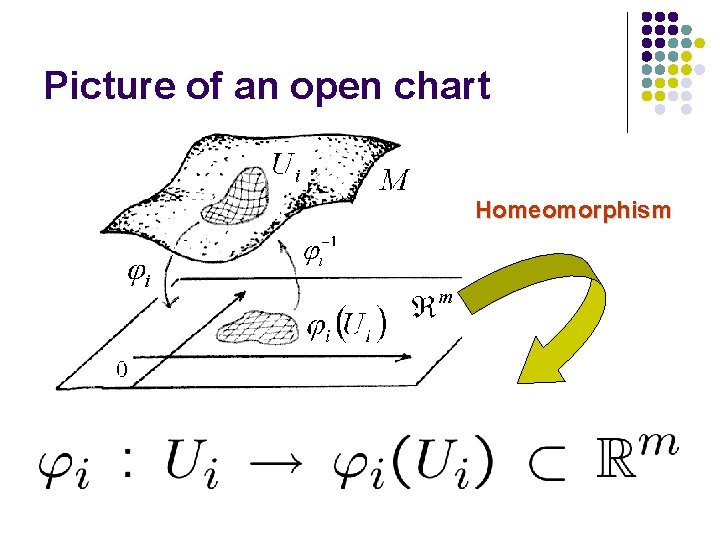
Open charts

Picture of an open chart Homeomorphism

Differentiable structure M 1

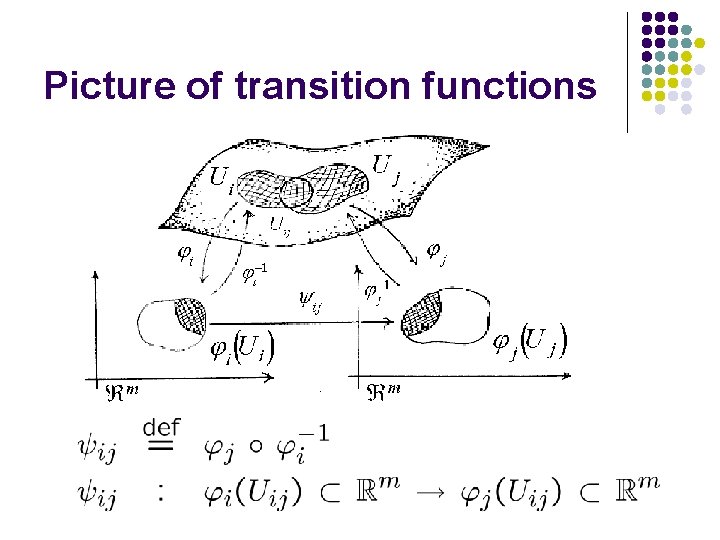
The axiom M 2 Transition functions

Picture of transition functions

The axiom M 3 Differentiable Manifolds

This is a constructive definition

Smooth manifolds

Complex Manifolds

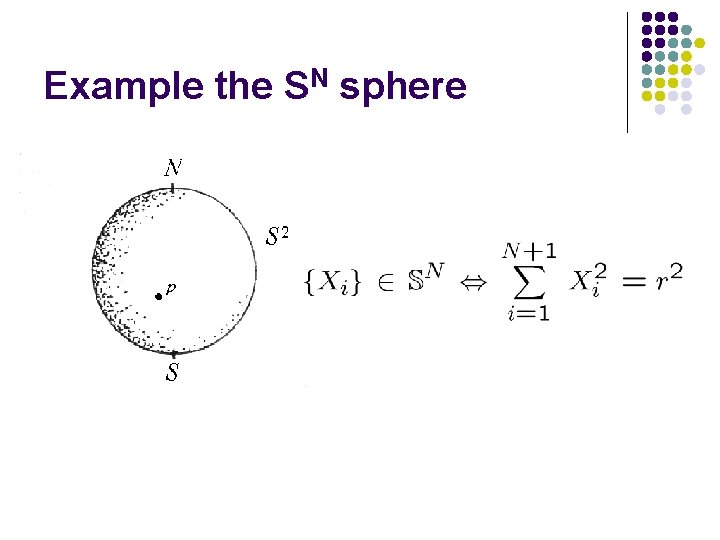
Example the SN sphere

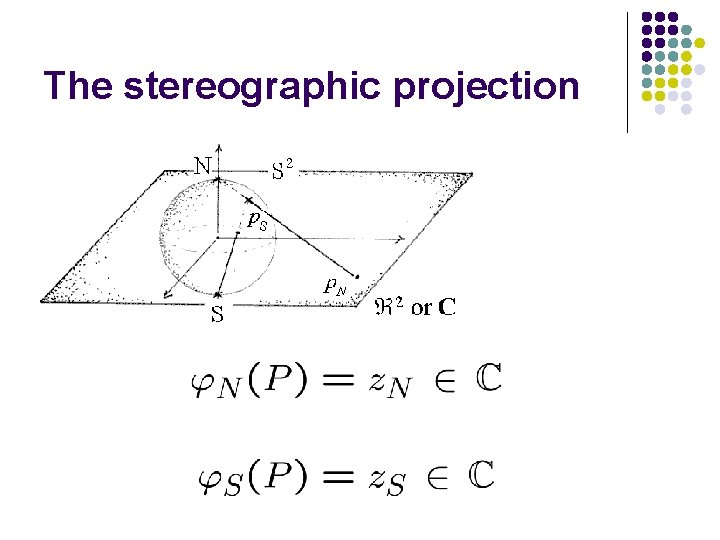
The stereographic projection

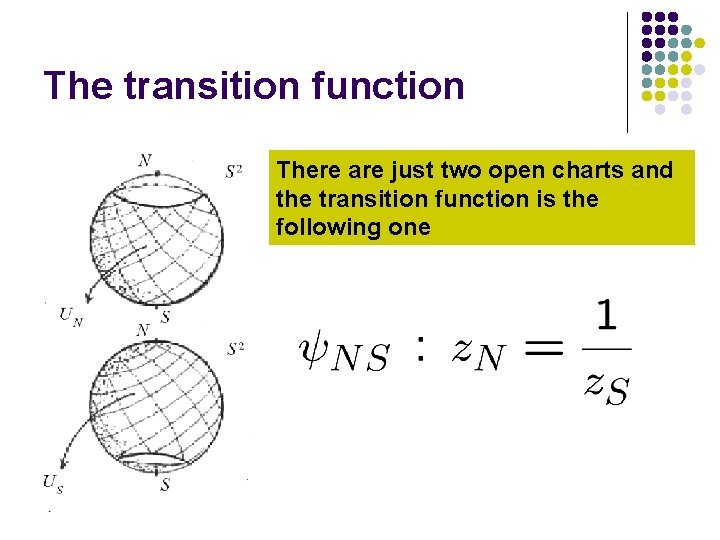
The transition function There are just two open charts and the transition function is the following one

Calculus on Manifolds

Functions on Manifolds

Local description

Gluing Rules

Global Functions

Germs of Smooth Functions

Germs at p 2 M

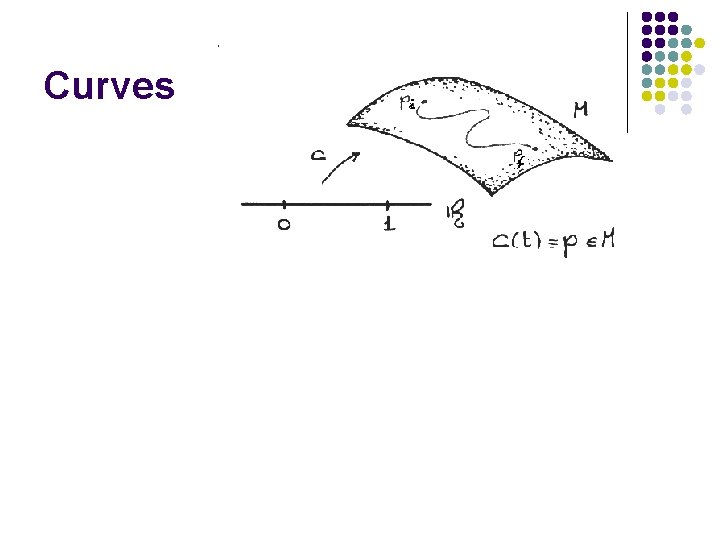
Towards tangent spaces: Curves on a Manifold

Curves

Loops

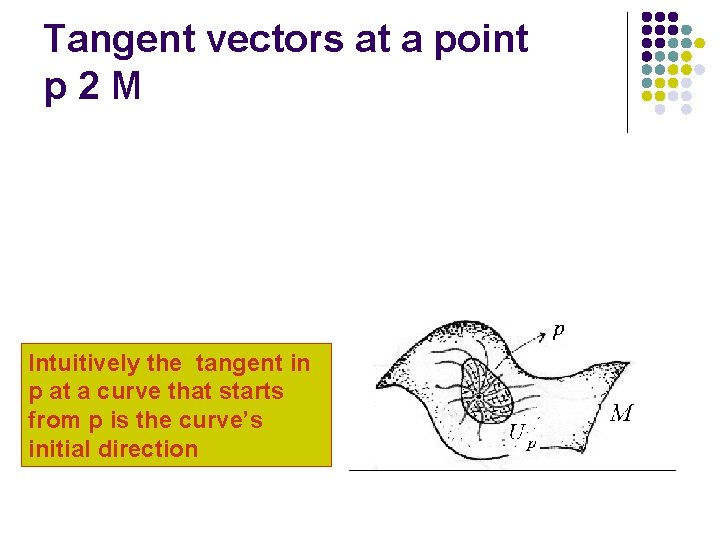
Tangent vectors at a point p 2 M Intuitively the tangent in p at a curve that starts from p is the curve’s initial direction

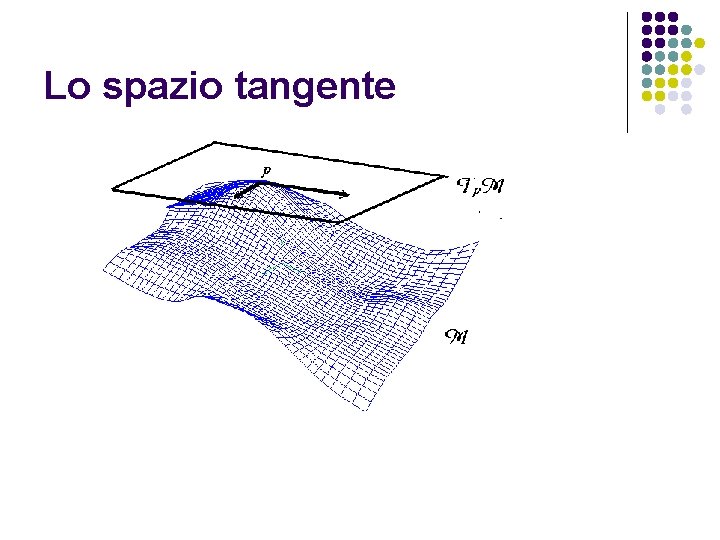
Tangent spaces at p 2 M

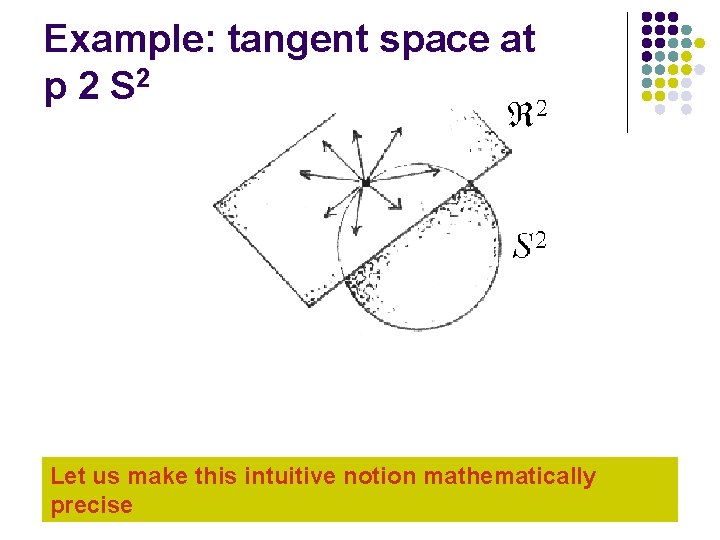
Example: tangent space at p 2 S 2 Let us make this intuitive notion mathematically precise

Tangent vectors and germs

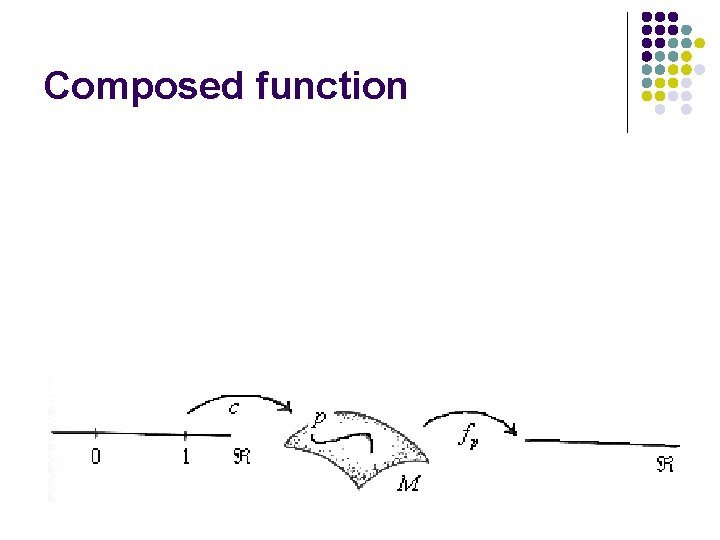
Composed function

Derivative = tangent vector

Differential operator

Tangent vectors and derivations of algebras Algebra of germs

Derivations of algebras

Vector space of derivations

Vectors as differential operators

Vector controvariance We have where

Controvariant versus covariant vectors

Introducing differential forms DEFINITION:

Cotangent space Definition

Differential 1 -forms at p 2 M = dx

Why named differential forms

Covariance

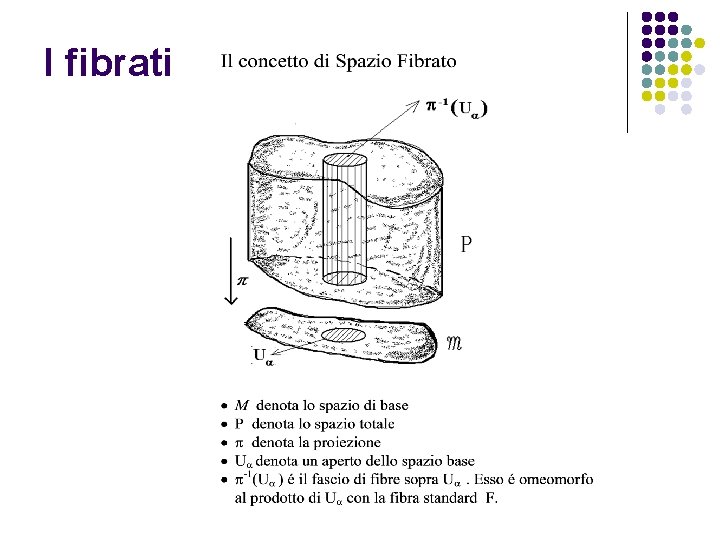
Fibre bundles

I fibrati

Lo spazio tangente

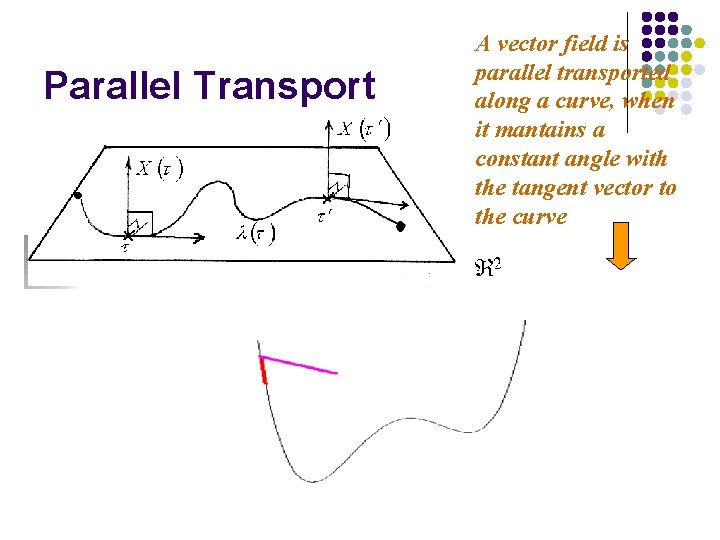
Parallel Transport A vector field is parallel transported along a curve, when it mantains a constant angle with the tangent vector to the curve

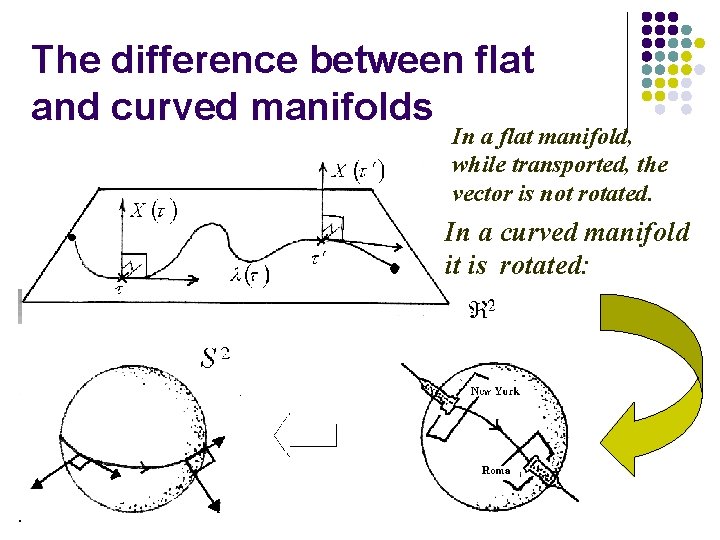
The difference between flat and curved manifolds In a flat manifold, while transported, the vector is not rotated. In a curved manifold it is rotated:

To see the real effect of curvature we must consider. . . Parallel transport along LOOPS After transport along a loop, the vector does not come back to the original position but it is rotated of some angle.

La 1 -forma di connessione

Riferimenti e potenziali vettori

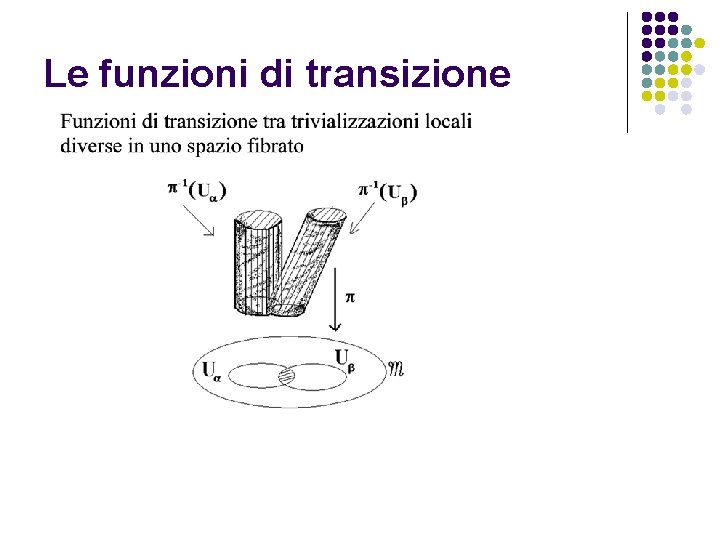
Le funzioni di transizione

Trasformazioni di gauge = cambio di trivializzazione locale


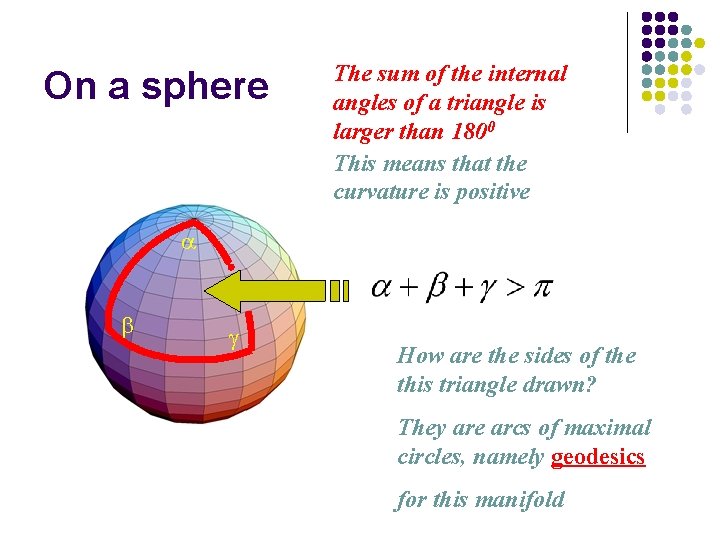
On a sphere The sum of the internal angles of a triangle is larger than 1800 This means that the curvature is positive a b g How are the sides of the this triangle drawn? They are arcs of maximal circles, namely geodesics for this manifold

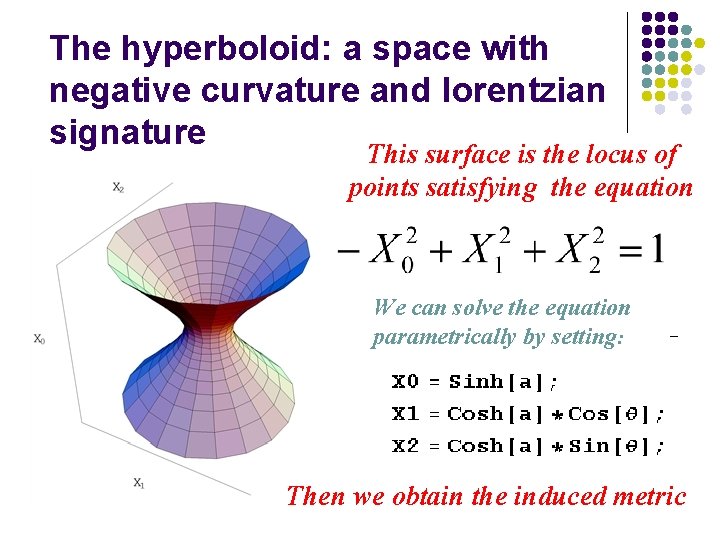
The hyperboloid: a space with negative curvature and lorentzian signature This surface is the locus of points satisfying the equation We can solve the equation parametrically by setting: Then we obtain the induced metric

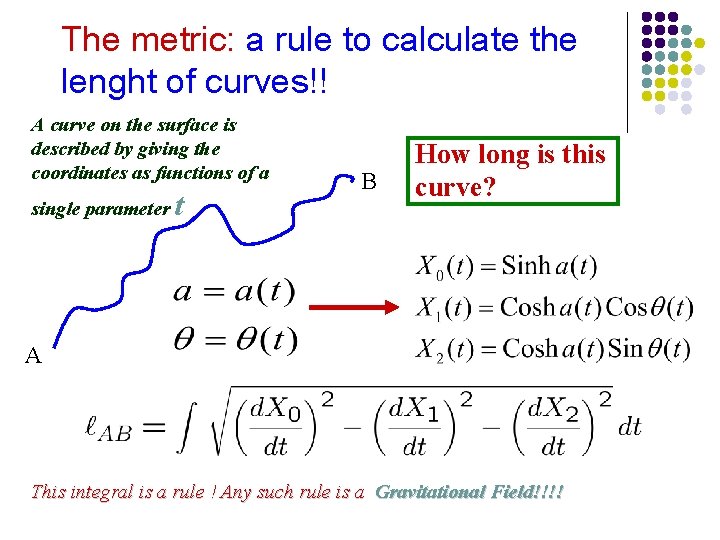
The metric: a rule to calculate the lenght of curves!! A curve on the surface is described by giving the coordinates as functions of a single parameter t B How long is this curve? A This integral is a rule ! Any such rule is a Gravitational Field!!!!

Underlying our rule for lengths is the induced metric: Where a and q are the coordinates of our space. This is a Lorentzian metric and it is just induced by the flat Lorentzian metric in three dimensions: using the parametric solution for X 0 , X 1 , X 2

What do particles do in a gravitational field? Answer: They just go straight as in empty space!!!! It is the concept of straight line that is modified by the presence of gravity!!!! The metaphor of Eddington’s sheet summarizes General Relativity. In curved space straight lines are different from straight lines in flat space!! The red line followed by the ball falling in the throat is a straight line (geodesics). On the other hand spacetime is bended under the weight of matter moving inside it!

The Methaphor as a Movie

What are the straight lines They are the geodesics, curves that do not change length under small deformations. These are the curves along which we have parallel transported our vectors On a sphere geodesics are maximal circles In the parallel transport the angle with the tangent vector remains fixed. On geodesics the tangent vector is transported parallel to itself.

Let us see what are the straight lines (=geodesics) on the Hyperboloid • ds 2 < 0 space-like geodesics: cannot be Three different types of geodesics Relativity = Lorentz signature -, + space time followed by any particle (it would travel faster than light) • ds 2 > 0 time-like geodesics. It is a possible worldline for a massive particle! • ds 2 = 0 light-like geodesics. It is a possible world-line for a massless particle like a photon Is the rule to calculate lengths

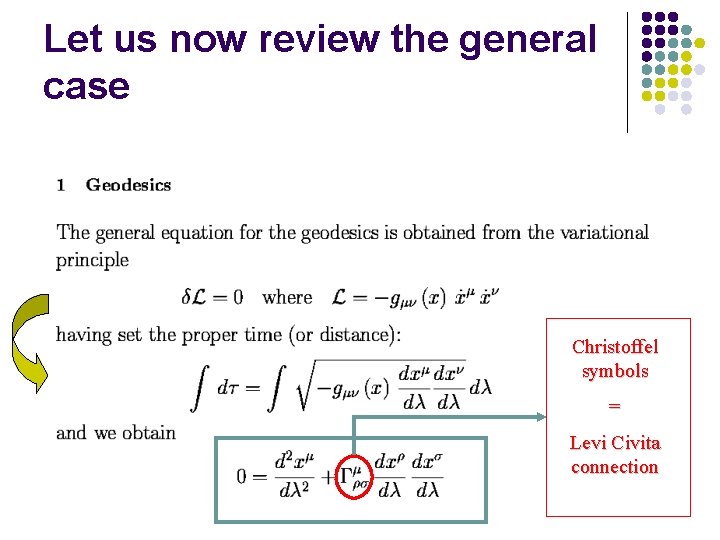
Deriving the geodesics from a variational principle

The Euler Lagrange equations are The conserved quantity p is, in the time-like or null-like cases, the energy of the particle travelling on the geodesic

Continuing. . . This procedure to obtain the differential equation of orbits extends from our toy model in two dimensions to more realistic cases in four dimensions: it is quite general

Still continuing Let us now study the shapes and properties of these curves

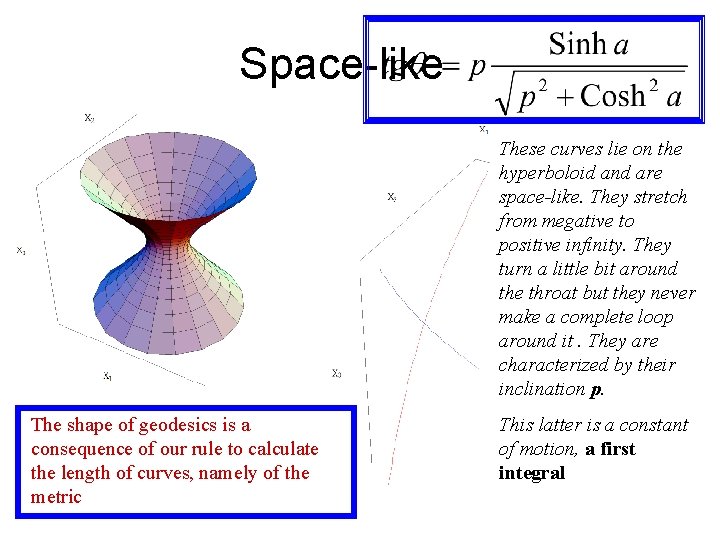
Space-like These curves lie on the hyperboloid and are space-like. They stretch from megative to positive infinity. They turn a little bit around the throat but they never make a complete loop around it. They are characterized by their inclination p. The shape of geodesics is a consequence of our rule to calculate the length of curves, namely of the metric This latter is a constant of motion, a first integral

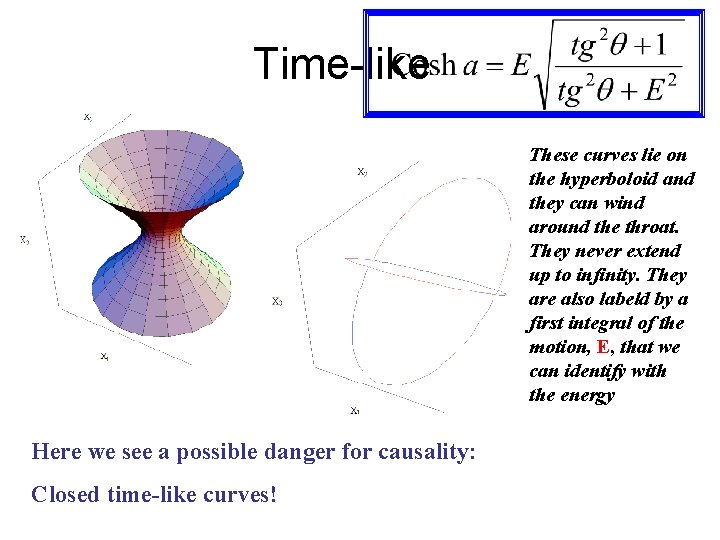
Time-like These curves lie on the hyperboloid and they can wind around the throat. They never extend up to infinity. They are also labeld by a first integral of the motion, E, that we can identify with the energy Here we see a possible danger for causality: Closed time-like curves!

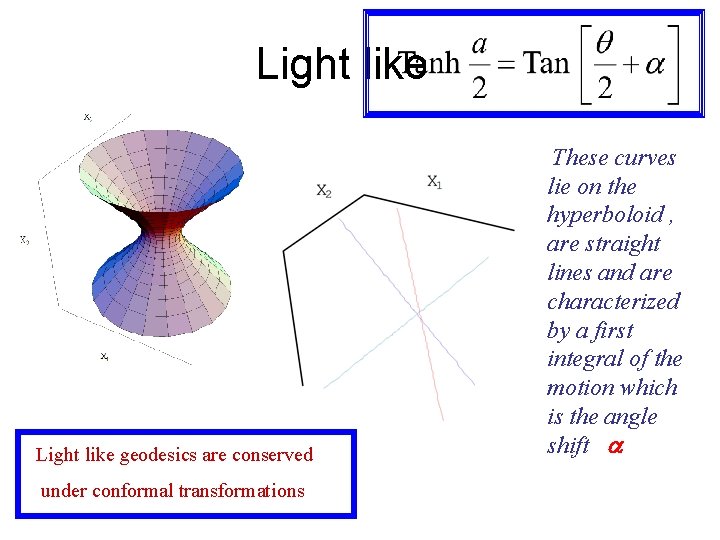
Light like geodesics are conserved under conformal transformations These curves lie on the hyperboloid , are straight lines and are characterized by a first integral of the motion which is the angle shift a

Let us now review the general case Christoffel symbols = Levi Civita connection

the Christoffel symbols are: Where from do they emerge and what is their meaning? ANSWER: They are the coefficients of an affine connection, namely the proper mathematical concept underlying the concept of parallel transport. Let us review the concept of connection

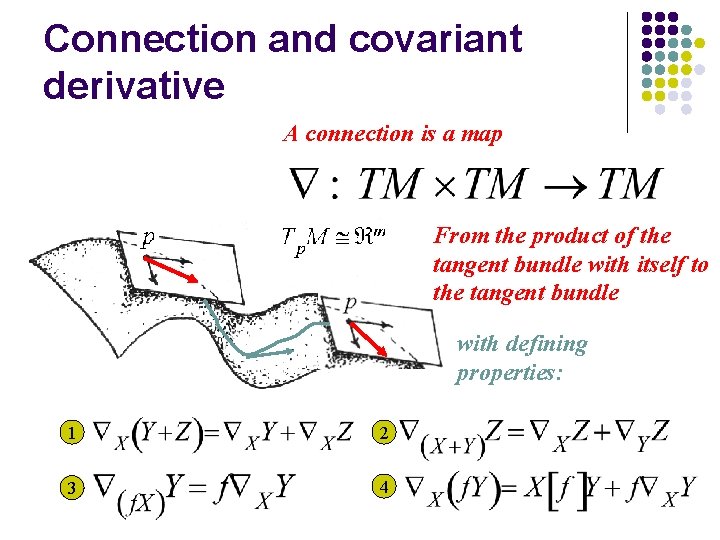
Connection and covariant derivative A connection is a map From the product of the tangent bundle with itself to the tangent bundle with defining properties: 1 2 3 4

In a basis. . . This defines the covariant derivative of a (controvariant) vector field

Torsion and Curvature Torsion Tensor Curvature Tensor aa The Riemann curvature tensor

If we have a metric. . . . An affine connection, namely a rule for the parallel transport can be arbitrarily given, but if we have a metric, then this induces a canonical special connection: THE LEVI CIVITA CONNECTION This connection is the one which emerges from the variational principle of geodesics!!!!!

 Fondamenti di pedagogia generale
Fondamenti di pedagogia generale Relativit
Relativit Corso generale sicurezza sul lavoro
Corso generale sicurezza sul lavoro Fondamenti di informatica 2
Fondamenti di informatica 2 Fondamenti di automatica benvenuti
Fondamenti di automatica benvenuti Fondamenti di sociologia giddens
Fondamenti di sociologia giddens I fondamenti dell'ict
I fondamenti dell'ict Marco schaerf
Marco schaerf Naturalismo francese e verismo italiano
Naturalismo francese e verismo italiano Impedenzimetro
Impedenzimetro Giovanni danese
Giovanni danese Genotipo
Genotipo Crisi dei fondamenti
Crisi dei fondamenti Reazione di riduzione
Reazione di riduzione Fondamenti di automatica unife
Fondamenti di automatica unife Fondamenti di astronomia
Fondamenti di astronomia 50 erros na liturgia
50 erros na liturgia Te invitamos hacer parte
Te invitamos hacer parte Este parte aquele parte
Este parte aquele parte Como se leen las fracciones del 1 al 20
Como se leen las fracciones del 1 al 20 Corso linguistica computazionale
Corso linguistica computazionale Corso opem c.r.i. slide
Corso opem c.r.i. slide Relazione finale scuola primaria compilata
Relazione finale scuola primaria compilata Slide corso rspp datore di lavoro rischio basso
Slide corso rspp datore di lavoro rischio basso Slide antincendio
Slide antincendio Corso gascromatografia napoli
Corso gascromatografia napoli Corso toeic bassano
Corso toeic bassano Slide corso formazione segnaletica stradale
Slide corso formazione segnaletica stradale Corso icq
Corso icq Corso vhdl
Corso vhdl Corso gascromatografia napoli
Corso gascromatografia napoli Corso trattori agricoli ppt
Corso trattori agricoli ppt Slide corso trattori agricoli
Slide corso trattori agricoli Slide corso macchine movimento terra
Slide corso macchine movimento terra Corso somministratori cils
Corso somministratori cils Edvard munch sera nel corso karl johann
Edvard munch sera nel corso karl johann Haccp ppt italiano
Haccp ppt italiano William paterson financial aid office
William paterson financial aid office Corso responsabile magazzino
Corso responsabile magazzino Slide corso ponteggi
Slide corso ponteggi Slide corso macchine movimento terra
Slide corso macchine movimento terra Presidente corso di laurea
Presidente corso di laurea Corso tutela del consumatore
Corso tutela del consumatore Corso oss poliambulanza
Corso oss poliambulanza Gru mobile autocarrata
Gru mobile autocarrata Slide corso sicurezza croce rossa
Slide corso sicurezza croce rossa Language
Language Corso negoziazione efficace
Corso negoziazione efficace Per una buona scrittura giuridica
Per una buona scrittura giuridica Corso mongo db
Corso mongo db Ecdl foundation
Ecdl foundation Corso monosettimanale significato
Corso monosettimanale significato Slide corso dpi terza categoria
Slide corso dpi terza categoria Corso dirigente accompagnatore basket
Corso dirigente accompagnatore basket Slide corso ple
Slide corso ple Corso valutazione investimenti
Corso valutazione investimenti Corso toscana 108
Corso toscana 108 Slide corso preposto ppt
Slide corso preposto ppt Sicsi
Sicsi Slide corso rspp
Slide corso rspp Liceo linguistico correggio
Liceo linguistico correggio Gestione per conto dello stato
Gestione per conto dello stato Corso dirigente accompagnatore calcio
Corso dirigente accompagnatore calcio Slide corso antincendio rischio basso
Slide corso antincendio rischio basso Open foam corso
Open foam corso Ic camigliano
Ic camigliano Corso allenatore di base basket
Corso allenatore di base basket Dispense del corso di sistemi energetici
Dispense del corso di sistemi energetici Test verifica corso carroponte pdf
Test verifica corso carroponte pdf Corso primo soccorso slide
Corso primo soccorso slide Corso di sociologia bagnasco barbagli cavalli
Corso di sociologia bagnasco barbagli cavalli Piercing lecce
Piercing lecce Manuale di pedagogia generale
Manuale di pedagogia generale Societe generale investor relations
Societe generale investor relations Studium generale wageningen
Studium generale wageningen V reparto comando generale carabinieri
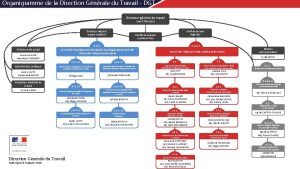
V reparto comando generale carabinieri Organigramme direction générale du travail
Organigramme direction générale du travail Diktámen
Diktámen Relatività generale liceo
Relatività generale liceo Loi générale des gaz
Loi générale des gaz Norme pai
Norme pai Grafic izoterma
Grafic izoterma Ginkgoale
Ginkgoale