Principii di Teoria Generale della Relativit F Garufi
























- Slides: 24

Principii di Teoria Generale della Relatività F. Garufi Complementi di Fisica – LM in Matematica

Introduction • General Relativity is the physical theory of gravity formulated by Einstein in 1916. It is based on the Equivalence Principle of Gravitation and Inertia, which establishes a fundamental connection between the gravitational field and the geometry of the space-time, and on the Principle of General Covariance. • The language of General Relativity is that of tensor analysis, or, in a more modern formulation, the language of differential geometry. • The first lecture will be dedicated to answer the following questions: 1) why does the Newtonian theory become inappropriate to describe the gravitational field. 2) why do we need a tensor to describe the gravitational field, and we need to introduce the concept of manifold, metric, affine connections and other geometrical objects. 3) What is the role played by the equivalence principle in all that. Principii di TRG - F. Garufi 2011 2

The Newtonian Theory • The Newtonian theory of gravity was published in 1685 in the “Philosophiae Naturalis Principia Mathematica”. It contains the cornerstones of classical physics, i. e. : Newton’s Law Newton’s Gravitaion Law Gravitational acceleration: depends on the relative distance ri of the massive test particle and the particles generating the field; G is the gravitational Constant. Principii di TRG - F. Garufi 2011 3

Principle of Equivalence • m. G/m. I is a constant for every massive body. • This has been already discovered by Galileo and Newton tested it studying the motion of pendulums of different composition, length and weight. • Since then a variety of experiments confirmed this crucial result. Among them Eötvos experiment in 1889 (accuracy of 1 part in 109), and Dicke experiment in 1964 (1 part in 1011) and Braginsky in 1972 (1 part in 1012). All the experiments up to our days confirm the Principle of Equivalence of the gravitational and the inertial mass. Principii di TRG - F. Garufi 2011 4

Principle of Equivalence • Let us consider the motion of a non relativistic particle subjected to arbitrary forces F and moving in a gravitational field that is constant. • Let us now jump on an elevator that is freely falling in the same gravitational field. • The observer on the falling elevator sees the same laws of physics as the other observer but without the gravitational field Principii di TRG - F. Garufi 2011 5

Principle of Equivalence • if g would not be constant the equation would contain additional terms containing the derivatives of g. However we can always consider an interval of time so short that g can be considered as constant • Therefore we can define this reference as a locally inertial frame. – If the gravitational field is constant and uniform everywhere, the coordinate transformation defines a locally inertial frame that will cover the whole spacetime. – If this is not the case we can set up a locally inertial frame only in the neighborhood of any given point. • Gravity is distinguished from all other forces because all bodies, given the same initial velocity, follow the same trajectory in a gravitational field, regardless of their internal constitution. This is not the case, for example, for electromagnetic forces, which act on charged but not on neutral bodies, and in any event the trajectories of charged particles depend on the ratio between charge and mass which is not the same for all particles. Principii di TRG - F. Garufi 2011 6

Principle of Equivalence • Strong form: In an arbitrary gravitational field, at any given space-time point, we can choose a locally inertial reference frame such that, in a sufficiently small region surrounding that point, all physical laws take the same form they would take in absence of gravity. • Weak form: as above replacing “all physical laws” by “the laws of motion of free falling bodies” Principii di TRG - F. Garufi 2011 7

The gravitational field in relativistic mechanics • A consequence of equivalence principle is that a non inetrial system is equivalent to a system with a gravitational field. • In an inertial system, the 4 -distance between two points in cartesian coordinates can be expressed as: ds 2= dt 2 -dx 2 -dy 2 -dz 2. • Upon transforming to any other inertial reference system (i. e. under Lorentz transformation) the interval, as we know, retains the same form. However, if we transform to a non-inertial system of reference will no longer be a sum of squares of the four coordinate differentials. Principii di TRG - F. Garufi 2011 8

The gravitational field in relativistic mechanics • Example: tranform to a uniformly rotating system: Principii di TRG - F. Garufi 2011 9

Geodesic equation as consequence of Equivalence principle • In a free falling system we can write: If we change the coordinates to a new frame: Multiplying by dx’γ/dxμ: Principii di TRG - F. Garufi 2011 10

Affine connections • The term Γαβγ is called the affine connection or Christoffel symbol. • The affine connection contains the second derivatives of the coordinates. Since the metric tensor contains the first derivatives: it is clear that Γαβγ will contain first derivatives of g. This can be shown explicitly. The result will be: Thus, in analogy with the newtonian law, we can say that the affine connections are the generalization of the newtonian gravitational field, and that the metric tensor is the generalization of the newtonian gravitational potential. Principii di TRG - F. Garufi 2011 11

The gravitational field in relativistic mechanics • So, in a non-inertial frame the 4 -dimensional coordinate system is curvilinear • The quantities gik determining all the geometric properties in each curvilinear system of coordinates, represent the space-time metric. • The quantities ηik define the Galilean system of coordinates. • An "actual" gravitational field cannot be eliminated by any transformation of coordinates. In other words, in the presence of a gravitational field space-time is such that the quantities gik determining its metric cannot, by any coordinate transformation, be brought to their Galilean values over all space. Principii di TRG - F. Garufi 2011 12

Curved geometry example • • • Let us consider two reference systems: K inertial and K’ rotating uniformly around the common axis A circle in the xy plane in the system K is a circle in the plane x’y’ of the K’ system. The ratio between circonference C and diameter measured with a scale in the K system is C/2 R = π In the system K’ the lengths measured at a radius R form center in the direction of motion experiment the Lorentz contraction, while the mesurement of diameter is unaffected by the motion => C/2 R > π In the general case the metric is not only noneuclidean but varies with time, and so, also the relationship between distance is variable. Thus is impossible to have a system of bodies fixed relative to one another. Principii di TRG - F. Garufi 2011 y R x 13

Curvilinear coordinates • Let us consider the transformation from a coordinate system xm to another x’m xm=fm(x’m) m=0, 1, 2, 3 => Any aggregate of 4 quantities that transforms as the coordinates differential is called a contravariant 4 -vector Am. Consider the derivatives of a scalar quantity with respect to the coordinates: Any aggregate of 4 quantities that transforms as the derivative of a scalar is called a covariant 4 -vector Am. Because two types of vectors appear in curvilinear coordinates, there are three types of tensors of the second rank. We call a contravariant tensor of the second rank, Amn, an aggregate of sixteen quantities which transform like the products of the components of two contravariant vectors, i. e. : covariant Principii di TRG - F. Garufi 2011 mixed 14

Curvilinear coordinates • Is easy to show that the scalar product of two 4 -vectors Am. Bn is invariant The transition between the different forms of a physical tensor is accomplished by using the metric tensor according to the formulas: Principii di TRG - F. Garufi 2011 15

Curvilinear coordinates • The transformation of the metric tensor helps to find the Jacobian of the transition from galilean to curvilinear coordinates • In curvilinear coordinates, the integration of a scalar quantity over the 4 -volume, is also a scalar, i. e. the 4 -volume element d 4 V is a scalar • On transforming to curvilinear coordinates xi, the element of integration d 4 V’ goes over into thus in curvilinear coordinates, when integrating over a four-volume the quantity √-g d 4 V behaves like an invariant. Principii di TRG - F. Garufi 2011 16

Distances and time intervals • First we find the relationship between the proper time τ and the x 0 coordinate. To do this let’s consider two infinitesimally separated events occurring at the same place in space: This represents the proper time for the given point in the space for a change of coordinate x 0. This implies also g 00>0. A tensor gik which does not satisfy this condition (and the signature) cannot correspond to any real gravitational field, i. e. cannot be the metric of a real space-time. Principii di TRG - F. Garufi 2011 17

Distances and time intervals • We now determine the element dl of spatial distance. In the special theory of relativity we can define dl as the interval between two infinitesimally separated events occurring at one and the same time. In the general theory of relativity it is impossible to determine dl by simply setting dx 0 = 0 in ds, since in a gravitational field the proper time at different points in space has a different dependence on the coordinate x 0. • Consider a light signal propagating from a point B of coordinates xα+dxα to the infinitesimaly near point A, of coordinate xα and back along the same path. • The time required, as observed from B is 2 l/c • The interval is: ds 2 = gmndx mdxn+2 g 0 mdx 0 dxm+g 00(dx 0)2 with the sum over the repeated latin indices from 0 to 3. • Solving the equation for ds 2 = 0 (since is the light round trip, the interval is of light type) we find two solutions corresponding to the light propagating in the two directions. Principii di TRG - F. Garufi 2011 18

Distances and time intervals The time for the round trip is: The corresponding proper time is given by multiplying by (g 00)1/2/c and the distance by a further multiplication by c/2: It is meaningless to integrate dl over a finite domain, since it depends on x 0; it makes sense only when gαβ is independent on time. Principii di TRG - F. Garufi 2011 19

Distances and time intervals • • Let’s come back to the concept of simultateous in GR, i. e. let’s try to synchrnonize clocks placed in different points in space. This can be achieved by sending light signals between two points. Consider the points A and B; we consider as simultaneous the moment at halfway the round trip, i. e. : x 0 -dx 0(2) x 0 • synchronization of clocks along a closed contour turns out to be impossible in general. In fact, starting out along the contour and returning to the initial point, we would obtain for Δx 0 a value different from zero, unless all g 0 m=0. In any gravitational field it is possible to choose a reference where this happens. x 0+dx 0(1) A Principii di TRG - F. Garufi 2011 B 20

Covariant derivative • In Euclidean geometry, the incremental ratio is obtained by transporting the quantity in a point A to a point B and dividing by the distance. • In a non Euclidean geometry, the concept of transport will not be anymore the same, due to curvature. Thus a new concept of derivative is needed to take into account the geometry of space-time Principii di TRG - F. Garufi 2011 21

Covariant derivative • If in the continuum is given a curve characterized by the arc length s starting from a fixed point on the curve, and given a scalar function f, then df/ds is also a scalar; • Thus, the quantity is an invariant for all the curves starting from a point in the continuum • The first term - the gradient of a scalar - is a covariant tensor. Principii di TRG - F. Garufi 2011 22

Covariant derivative • If we compute the ratio: it is also an invariant, thus: Now it comes into play the concepr of transport: let’s assume the transport is made along the geodetic: Principii di TRG - F. Garufi 2011 23

Covariant derivative • The expression into parethesis is symmetrical and, since from a point in the contunuum it is possible to draw a geodetic in any direction, we can define a second order covariant tensor: that we will call the covariant derivative of Am. Principii di TRG - F. Garufi 2011 24
 Relativit
Relativit Petitio principii adalah
Petitio principii adalah Profesor c++
Profesor c++ Amphiboly fallacy
Amphiboly fallacy Falacia petitio principii ejemplos
Falacia petitio principii ejemplos Principii orizontale
Principii orizontale Jakobson teoria della comunicazione
Jakobson teoria della comunicazione Teoria della dipendenza di deutsch e gerard
Teoria della dipendenza di deutsch e gerard Teoria atomica della materia
Teoria atomica della materia Aristotele teoria della conoscenza
Aristotele teoria della conoscenza Multiculturalit
Multiculturalit Teoria della lubrificazione
Teoria della lubrificazione Problema thog
Problema thog Teoria della processabilità pienemann
Teoria della processabilità pienemann Teoria quantitativa della moneta
Teoria quantitativa della moneta Prochaska model
Prochaska model Teoria della detenzione del segnale
Teoria della detenzione del segnale Teoria cinetico molecolare della materia
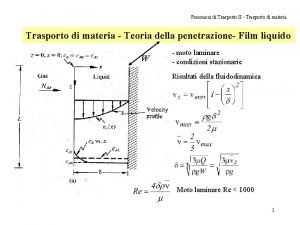
Teoria cinetico molecolare della materia Teoria della penetrazione
Teoria della penetrazione Teoria del legame di valenza zanichelli
Teoria del legame di valenza zanichelli Sperber e wilson
Sperber e wilson Teoria della scelta razionale
Teoria della scelta razionale Dalle leggi della chimica alla teoria atomica
Dalle leggi della chimica alla teoria atomica Teoria della programmazione lineare
Teoria della programmazione lineare Teoria della dominanza sociale
Teoria della dominanza sociale