Computational Geometry 2 D Convex Hulls Joseph S

Computational Geometry 2 D Convex Hulls Joseph S. B. Mitchell Stony Brook University Chapter 2: Devadoss-O’Rourke

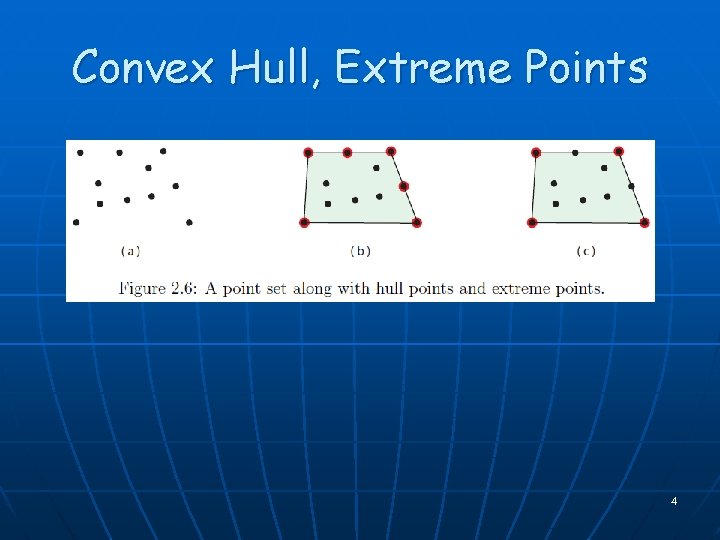
Convexity n n p p q q Set X is convex if p, q X pq X convex non-convex Point p X is an extreme point if there exists a line (hyperplane) through p such that all other points of X lie strictly to one side Extreme points in red r q p 2

Convex Hull 3

Convex Hull, Extreme Points 4

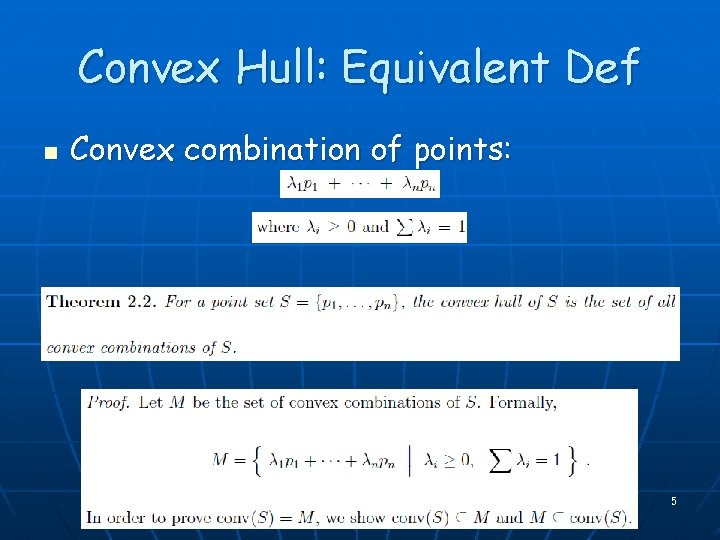
Convex Hull: Equivalent Def n Convex combination of points: 5

Convex Hull: Equivalent Defs 6

Equivalent Definitions of Convex Hull, CH(X) n n {all convex combinations of d+1 points of X } [Caratheodory’s Thm] (in any dimension d) Devadoss-O’Rourke Def n n Set-theoretic “smallest” convex set containing X. In 2 D: min-area (or min-perimeter) enclosing convex body containing X In 2 D: 7

Convex Hull in 2 D n Fact: If X=S is a finite set of points in 2 D, then CH(X) is a convex polygon whose vertices (extreme points) are points of S. 8

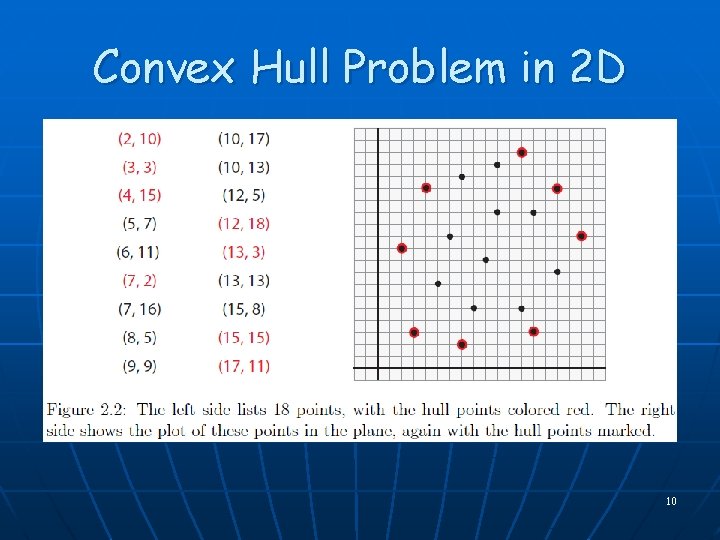
Fundamental Algorithmic Problem: 2 D Convex Hulls n Input: n points S = (p 1, p 2, …, pn) p 2 p 8 p 7 p 4 p 3 p 5 Output: (9, 6, 4, 2, 7, 8, 5) n More generally: CH(polygons) p 1 p 6 p 9 Output: A boundary representation, e. g. , ordered list of vertices (extreme points), of the convex hull, CH(S), of S (convex polygon) 9

Convex Hull Problem in 2 D 10

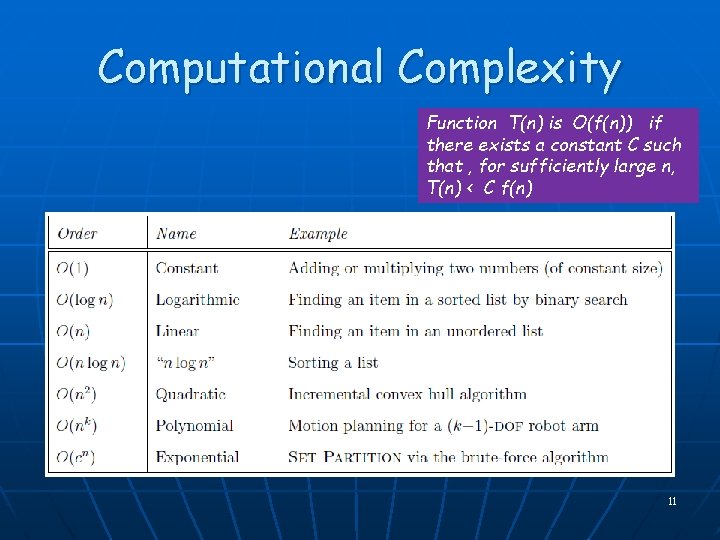
Computational Complexity Function T(n) is O(f(n)) if there exists a constant C such that , for sufficiently large n, T(n) < C f(n) 11

Comparing O(n), O(n log n), O(n 2) n n log n Function T(n) is O(f(n)) if there exists a constant C such that , for sufficiently large n, T(n) < C f(n) n² 210 10³ 10 • 210 104 220 106 20 • 220 2 • 107 240 1012 Interactive Processing 220 106 n log n algorithms n² algorithms n = 1000 yes ? n = 1000000 ? no 12

2 D Convex Hull Algorithms n n O(n 4) O(n 3) O(n 2) O(nh) • n n n simple, brute force (but finite!) still simple, brute force incremental algorithm [DO] Section 2. 2 simple, “output-sensitive” h = output size (# vertices) O(n log n) worst-case optimal (as fcn of n) O(n log h) “ultimate” time bound (as fcn of n, h) Randomized, expected O(n log n) 13

Lower Bound n Lower bound: (n log n) [DO] Section 2. 5 y= x 2 (xi , xi 2 ) From SORTING: xi Note: Even if the output of CH is not required to be an ordered list of vertices (e. g. , just the # of vertices), (n log n) holds As function of n and h: (n log h) holds 14

Lower Bound [DO] Section 2. 5 computing the ordered convex hull of n points in the plane. 15

Lower Bound [DO] Section 2. 5 computing the ordered convex hull of n points in the plane. An even stronger statement is true: 16

Primitive Computation • “Left” tests: sign of a cross product (determinant), which determines the orientation of 3 points • Time O(1) (“constant”) c Left( a, b, c ) = TRUE ab ac > 0 a b c is left of ab 17

Super. Stupid. CH: O(n 4) n n Fact: If s ∆pqr, then s is not a vertex q of CH(S) p s p • q p O(n 3) r n r p, q • s p, q, r: If s ∆pqr then mark s as NON-vertex n n O(n) Output: Vertices of CH(S) Can sort (O(n log n) ) to get ordered 18

Stupid. CH: O(n 3) n n Fact: If all points of S lie strictly to one side of the line pq or lie in between p and q, then pq is an edge of CH(S). p q p O(n 2) • q p r • r p, q: If r red then mark pq as NON-edge (ccw) n n O(n) Output: Edges of CH(S) Can sort (O(n log n) ) to get ordered Caution!! Numerical errors require care to avoid crash/infinite loop! Applet by Snoeyink 19

Incremental Algorithm [DO] Section 2. 2 20

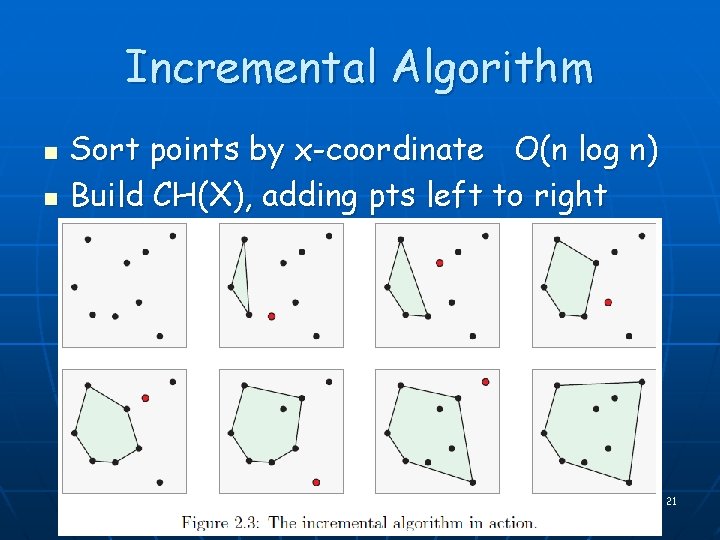
Incremental Algorithm n n Sort points by x-coordinate O(n log n) Build CH(X), adding pts left to right 21

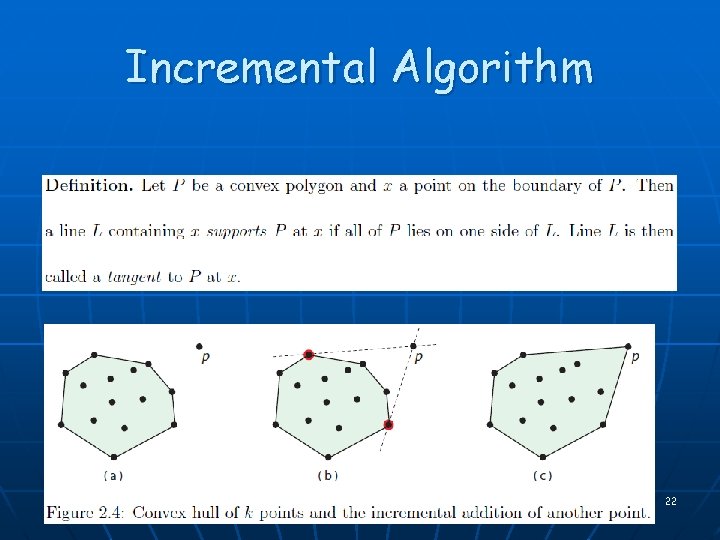
Incremental Algorithm 22

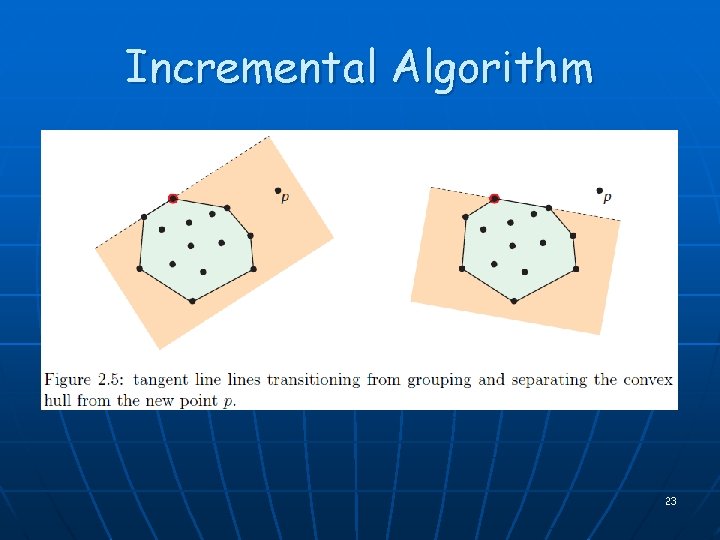
Incremental Algorithm 23

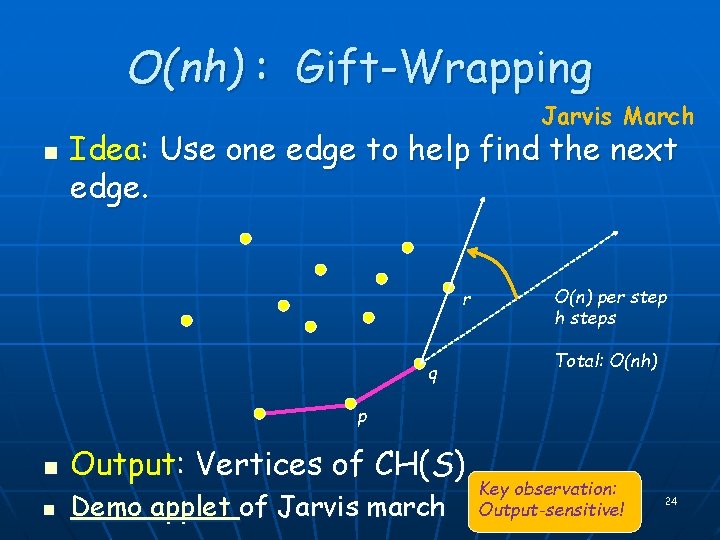
O(nh) : Gift-Wrapping Jarvis March n Idea: Use one edge to help find the next edge. r q O(n) per step h steps Total: O(nh) p n n Output: Vertices of CH(S) Demo applet of Jarvis march Key observation: Output-sensitive! 24

Gift-Wrapping [DO] Section 2. 4 25

Gift-Wrapping [DO] Section 2. 4 26

O(n log n) : Graham Scan n n Idea: Sorting helps! Start with vlowest (min-y), a known vertex O(n log n) Sort S by angle about vlowest Graham scan: O(n) • Maintain a stack representing (left-turning) CH so far n n Demo applet If pi is left of last edge of stack, then PUSH Else, POP stack until it is left, charging work to popped points vlowest CH so far 28

[DO] Section 2. 4 Graham Scan Red points form right turn, so are discarded 29

Graham Scan [DO] Section 2. 4 30

Graham Scan Sorted points: [O’Rourke, Chapter 3] 31

[O’Rourke, Chapter 3] 32

[O’Rourke, Chapter 3] Stack History 33

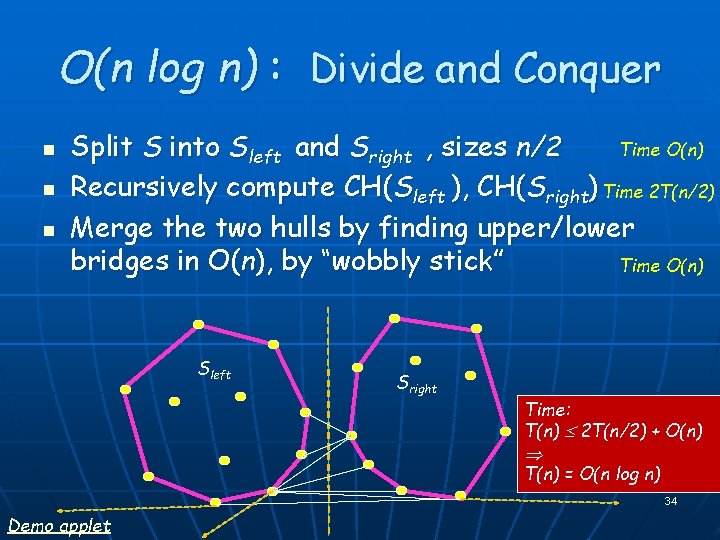
O(n log n) : Divide and Conquer n n n Time O(n) Split S into Sleft and Sright , sizes n/2 Recursively compute CH(Sleft ), CH(Sright) Time 2 T(n/2) Merge the two hulls by finding upper/lower bridges in O(n), by “wobbly stick” Time O(n) Sleft Sright Time: T(n) 2 T(n/2) + O(n) T(n) = O(n log n) 34 Demo applet

Divide and Conquer [DO] Section 2. 6 35

Divide and Conquer [DO] Section 2. 6 36

Divide and Conquer [DO] Section 2. 6 37

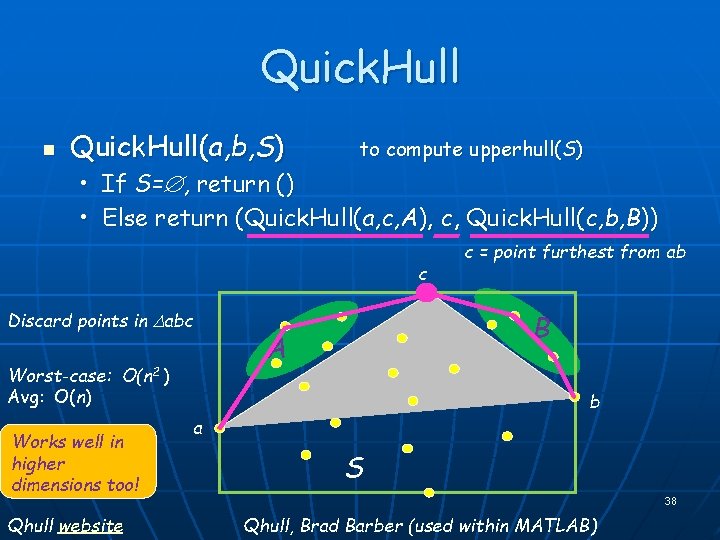
Quick. Hull n Quick. Hull(a, b, S) to compute upperhull(S) • If S= , return () • Else return (Quick. Hull(a, c, A), c, Quick. Hull(c, b, B)) c Discard points in abc Works well in higher dimensions too! Qhull website B A Worst-case: O(n 2 ) Avg: O(n) c = point furthest from ab b a S 38 Qhull, Brad Barber (used within MATLAB)

Quick. Hull n Applet (programmed by Jeff So) Applet (by Lambert) n When is it “bad”? (see hw 2) n • If no points are discarded (in abc), at each iteration, and • The “balance” may be very lop-sided (between sets A and B; in fact, one set could be empty, at every iteration!) 39

Quick. Hull [David Mount lecture notes, Lecture 3] 40

O(n log n) : Incremental Construction n n Add points in the order given: v 1 , v 2 , …, vn Maintain current Qi = CH(v 1 , v 2 , …, vi ) Point location test: Add vi+1 : O(log n) AMS 545 / CSE 555 • If v Q , do nothing n i+1 i • Else insert vi+1 by finding tangencies, updating the hull n n Binary search: O(log n) Worst-case cost of insertion: O(log n) But, uses complex data structures 41

O(n log n) : Randomized Incremental n n Add points in random order Keep current Qi = CH(v 1 , v 2 , …, vi ) Add vi+1 : AMS 545 / CSE 555 • If v Q , do nothing n i+1 i • Else insert vi+1 by finding tangencies, updating the hull n Expected cost of insertion: O(log n) 42

n n Each uninserted vj Qi (j>i+1) points to the bucket (cone) containing it; each cone points to the list of uninserted vj Qi within it (with its conflict edge) Add vi+1 Qi : • Start from “conflict” edge e, and walk cw/ccw to establish new tangencies from vi+1 , charging walk to deleted vertices • Rebucket points in affected cones (update lists for each bucket) • Total work: O(n) + rebucketing work • E(rebucket cost for vj at step i) = O(1) P(rebucket) O(1) (2/i ) = O(1/i ) AMS 545 / CSE 555 v j E(total rebucket cost for vj ) = = O(log n) Total expected work = O(n log n) e vi+1 Backwards Analysis: vj was just rebucketed iff the O(1/i ) last point inserted was one of the 2 endpoints of the (current) 43 conflict edge, e, for vj

Output-Sensitive: O(n log h) n The “ultimate” convex hull (in 2 D) • “Marriage before Conquest” : O(n log h) h = output size • Lower bound (n log h) [Kirkpatrick & Seidel’ 86] So, O(n log h) is BEST AMS 545 / CSE 555 Simpler [Chan’ 95] n n 2 Ideas: POSSIBLE, as function of n and h !! • Break point set S into groups of appropriate size m (ideally, m = h) • Search for the “right” value of m ( =h, which we do not know in advance) by repeated squaring 44

Chan’s Algorithm n Break S into n/m groups, each of size m • Find CH of each group (using, e. g. , Graham scan): n O(m log m) per group, so total O((n/m) m log m) = O(n log h) AMS 545 / CSE 555 n Gift-wrap the n/m hulls to get overall CH: • At each gift-wrap step, when pivoting around vertex v n n find the tangency point (binary search, O(log m)) to each group CH pick the smallest angle among the n/m tangencies: • O( h (n/m) log m) n n = O( h (n/h) log h) = O(n log h) Hope: m=h Try m = 4, 16, 256, 65536, … O(n ( log (221 ) + log (222 ) + log (223 ) + … log (22 log (h)) ) = O(n (21 + 22 + 23 + … + 2 log (h)) )) = O(n (2 log h)) = O(n log h) v v 45

CH of Simple Chains/Polygons n n n Input: ordered list of points that form a simple chain/cycle Importance of simplicity (noncrossing, Jordan curve) as a means of “sorting” (vs. sorting in x, y) Melkman’s Algorithm: O(n) (vs. O(n log n) or O(n log h)) 1 2 n 46

Melkman’s Algorithm Keep hull in DEQUE: < vb , vb+1 , …, vt-1 , vt =vb > While Left(vb , vb+1 , vi ) and Left(vt-1 , vt , vi ) vt-1 i i+1 Remove vb+1 , vb+2 , … vt vt-1 and vt-1 , vt-2 , … vb until convexity restored vi vi New vb =vt = vi vt vb+1 vb vb+1 Claim: Simplicity assures that the only way for the chain to exit the current hull is via pockets vb vb+1 or vt-1 vt. Time: O(n), since O(1) per insertion Simplicity helps! 47

Melkman’s Algorithm 48

Melkman’s Algorithm 49

Melkman’s Algorithm 50

Expected Size of CH 51

Expected Size, h, of CH n n n Claim: For n points uniform in a square, the expected number of maximal points is O(log n) CH vertices are Corollary: E(h) = O(log n) (since subset of maximal points) Thus, Gift-Wrap/Jarvis runs in expected O(n log n), if points are uniform in a box, etc. 52

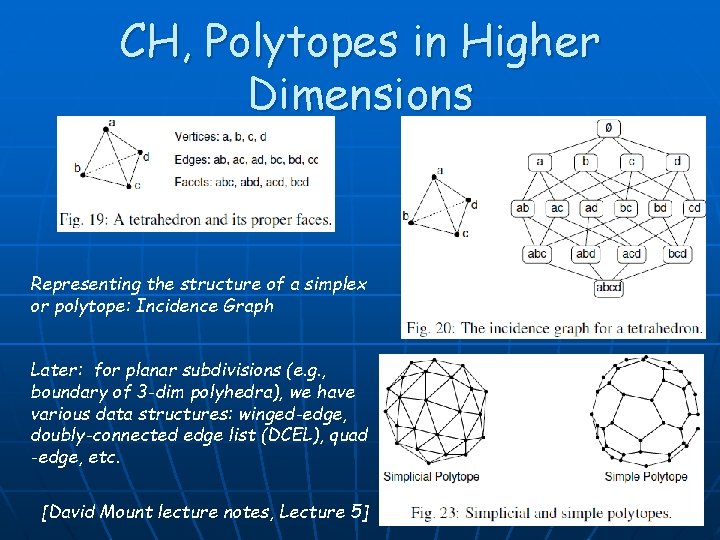
CH, Polytopes in Higher Dimensions 53

CH, Polytopes in Higher Dimensions Representing the structure of a simplex or polytope: Incidence Graph Later: for planar subdivisions (e. g. , boundary of 3 -dim polyhedra), we have various data structures: winged-edge, doubly-connected edge list (DCEL), quad -edge, etc. [David Mount lecture notes, Lecture 5] 54

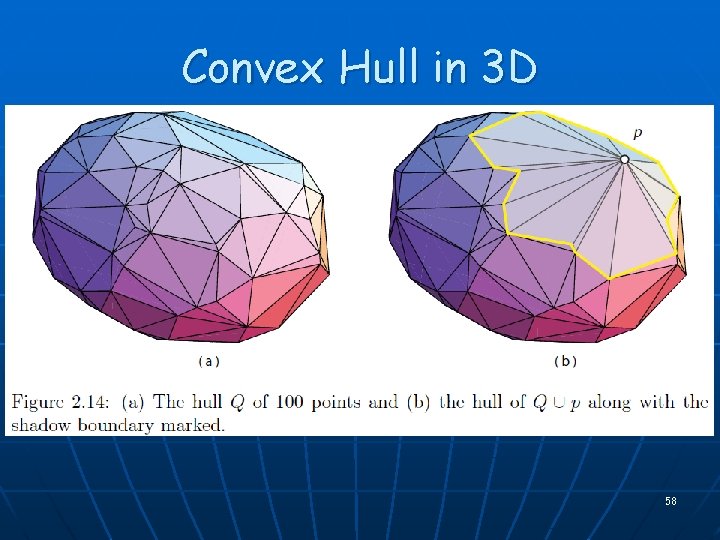
Convex Hull in 3 D 55

Convex Hull in 3 D 56

CH in Higher Dimensions n 3 D: Divide and conquer: • T(n) 2 T(n/2) + O(n) merge • O(n log n) • Output-sensitive: O(n log h) [Chan] n applet h= O(n) Higher dimensions: (d 4) • O(n d/2 ), which is worst-case OPT, since point sets exist with h= (n d/2 ) • Output-sensitive: O((n+h) logd-2 h), for d=4, 5 57 Qhull website

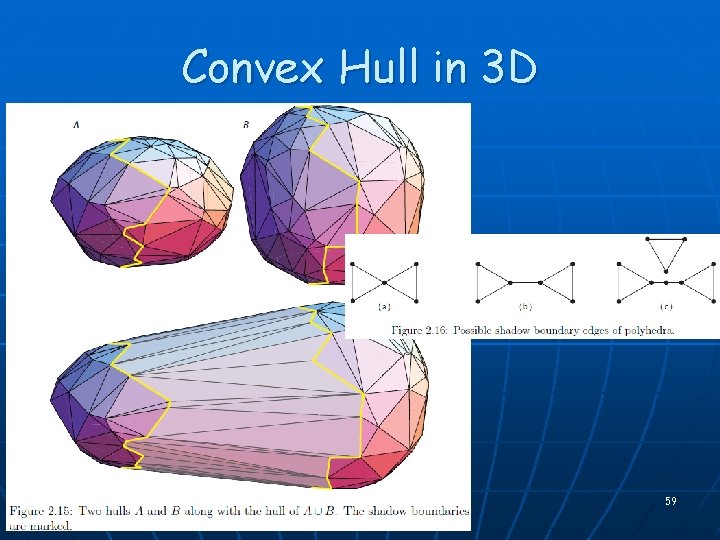
Convex Hull in 3 D 58

Convex Hull in 3 D 59

More Demos n n n Various 2 D and 3 D algorithms in an applet Applets of algorithms in O’Rourke’s book Applets from Jack Snoeyink 60

Review: Convex Hull Algorithms n n n n O(n 4), O(n 3), naïve O(n 2) incremental algorithm O(nh) simple, “output-sensitive” O(n log n) Graham scan, divide-and-conquer, incremental (with fancy data structures); worst-case optimal (as fcn of n) O(n log h) “ultimate” time bound (as fcn of n, h) Randomized, expected O(n log n) (simple) 3 D: Divide and conquer: O(n log n) • Output-sensitive: O(n log h) [Chan] n Higher dimensions: (d 4) • O(n d/2 ), which is worst-case OPT, • Output-sensitive: O((n+h) logd-2 h), for d=4, 5 61