CMPS 3120 Computational Geometry Spring 2013 Convex Hulls

CMPS 3120: Computational Geometry Spring 2013 Convex Hulls II Carola Wenk 1/17/13 CMPS 3120: Computational Geometry 1

q 1 q 2 Jarvis’ March (Gift Wrapping) Algorithm Giftwrapping_CH(P): // Compute CH(P) by incrementally inserting points from left to right Input: Point set P R 2 Output: List q 1, q 2, … of vertices in counter-clockwise order around CH(P) q 1 = lexicographically smallest point in P q 2 = point in P with smallest angle to horizontal line through q 1 i=2 do { i++ qi = point with smallest angle to line through qi-2 and qi-1 } while qi ≠ p 1 q 3 • Runtime: O(hn) , where n = |P| and h = #points on CH(P) • Output-sensitive algorithm 1/17/13 CMPS 3120: Computational Geometry 2

Incremental Insertion Algorithm Incremental_CH(P): // Compute CH(P) by incrementally inserting points from left to right Input: Point set P R 2 Output: C=CH(P), described as a list of vertices in counter-clockwise order O(n log n) Sort points in P lexicographically (by x-coordinate, break ties by y-coordinate) O(1) Remove first three points from P and insert them into C in counter-clockwise order around the triangle described by them. n-3 times for all p P // Incrementally add p to hull O(i) Compute the two tangents to p and C O(i) Remove enclosed non-hull points from C, and insert p n 2) , where n = |P| • Runtime: O( i = n i=3 • Really? 1/17/13 CMPS 3120: Computational Geometry 3

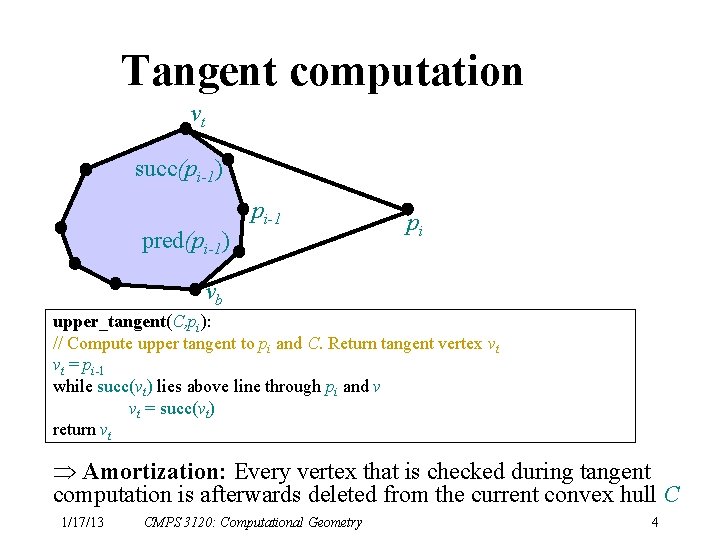
Tangent computation vt succ(pi-1) pred(pi-1) pi-1 pi vb upper_tangent(C, pi): // Compute upper tangent to pi and C. Return tangent vertex vt vt = pi-1 while succ(vt) lies above line through pi and v vt = succ(vt) return vt Amortization: Every vertex that is checked during tangent computation is afterwards deleted from the current convex hull C 1/17/13 CMPS 3120: Computational Geometry 4

Incremental Insertion Algorithm Incremental_CH(P): // Compute CH(P) by incrementally inserting points from left to right Input: Point set P R 2 Output: C=CH(P), described as a list of vertices in counter-clockwise order O(n log n) Sort points in P lexicographically (by x-coordinate, break ties by y-coordinate) O(1) Remove first three points from P and insert them into C in counter-clockwise order around the triangle described by them. n-3 times for all p P // Incrementally add p to hull O(1) amort. Compute the two tangents to p and C Remove enclosed non-hull points from C, and insert p O(1) amort. • Runtime: O(n log n + n) = O(n log n), where n = |P| 1/17/13 CMPS 3120: Computational Geometry 5

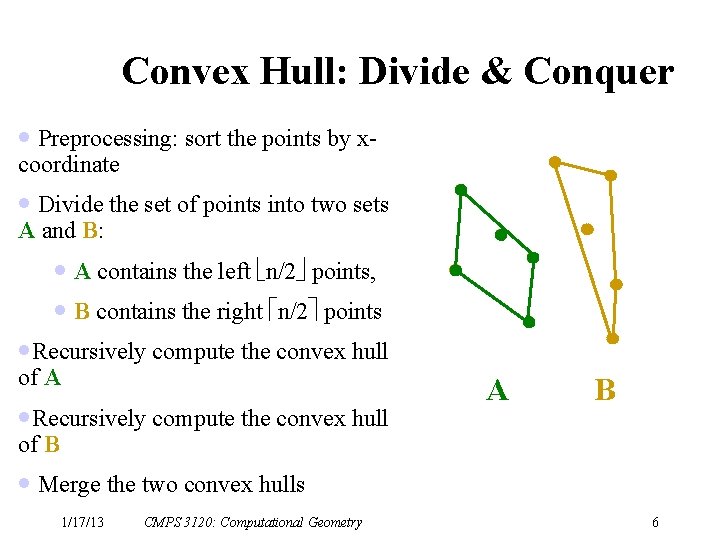
Convex Hull: Divide & Conquer · Preprocessing: sort the points by xcoordinate · Divide the set of points into two sets A and B: · A contains the left n/2 points, · B contains the right n/2 points ·Recursively compute the convex hull of A ·Recursively compute the convex hull A B of B · Merge the two convex hulls 1/17/13 CMPS 3120: Computational Geometry 6

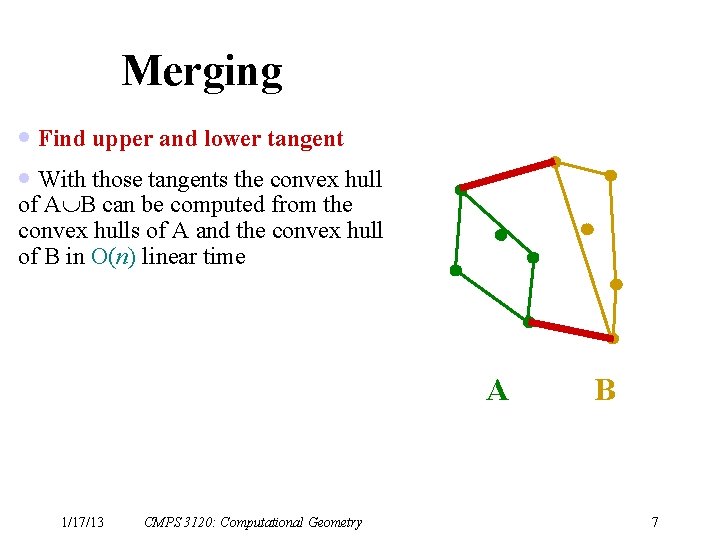
Merging · Find upper and lower tangent · With those tangents the convex hull of A B can be computed from the convex hulls of A and the convex hull of B in O(n) linear time A 1/17/13 CMPS 3120: Computational Geometry B 7

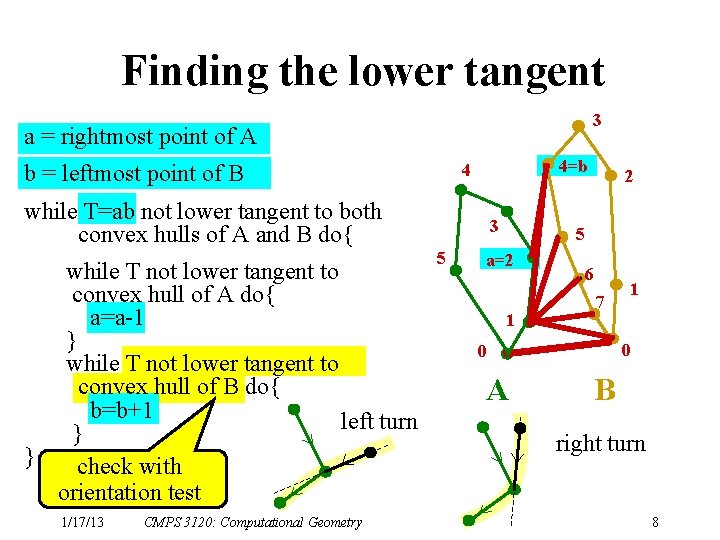
Finding the lower tangent 3 a = rightmost point of A b = leftmost point of B 4=b 4 while T=ab not lower tangent to both convex hulls of A and B do{ while T not lower tangent to convex hull of A do{ a=a-1 } while T not lower tangent to convex hull of B do{ b=b+1 left turn } } check with orientation test 1/17/13 CMPS 3120: Computational Geometry 3 5 2 5 a=2 1 6 7 0 0 A 1 B right turn 8

Convex Hull: Runtime · Preprocessing: sort the points by xcoordinate · Divide the set of points into two sets A and B: O(n log n) just once O(1) · A contains the left n/2 points, · B contains the right n/2 points ·Recursively compute the convex hull T(n/2) · Merge the two convex hulls O(n) of A of B 1/17/13 CMPS 3120: Computational Geometry 9

Convex Hull: Runtime · Runtime Recurrence: T(n) = 2 T(n/2) + cn · Solves to T(n) = (n log n) 1/17/13 CMPS 3120: Computational Geometry 10

Recurrence (Just like merge sort recurrence) 1. Divide: Divide set of points in half. 2. Conquer: Recursively compute convex hulls of 2 halves. 3. Combine: Linear-time merge. T(n) = 2 T(n/2) + O(n) work dividing # subproblems subproblem size and combining 1/17/13 CMPS 3120: Computational Geometry 11

Recurrence (cont’d) T(n) = (1) if n = 1; 2 T(n/2) + (n) if n > 1. • How do we solve T(n)? I. e. , how do we find out if it is O(n) or O(n 2) or …? 1/17/13 CMPS 3120: Computational Geometry 12

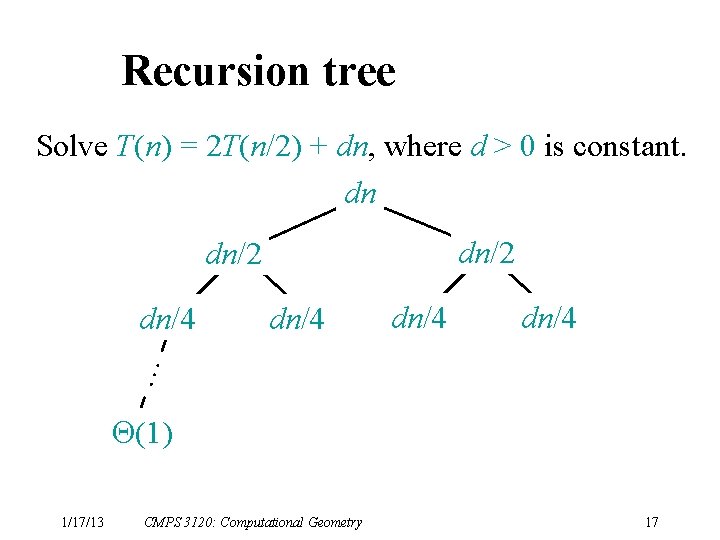
Recursion tree Solve T(n) = 2 T(n/2) + dn, where d > 0 is constant. 1/17/13 CMPS 3120: Computational Geometry 13

Recursion tree Solve T(n) = 2 T(n/2) + dn, where d > 0 is constant. T(n) 1/17/13 CMPS 3120: Computational Geometry 14

Recursion tree Solve T(n) = 2 T(n/2) + dn, where d > 0 is constant. dn T(n/2) 1/17/13 CMPS 3120: Computational Geometry T(n/2) 15

Recursion tree Solve T(n) = 2 T(n/2) + dn, where d > 0 is constant. dn dn/2 T(n/4) 1/17/13 T(n/4) CMPS 3120: Computational Geometry dn/2 T(n/4) 16

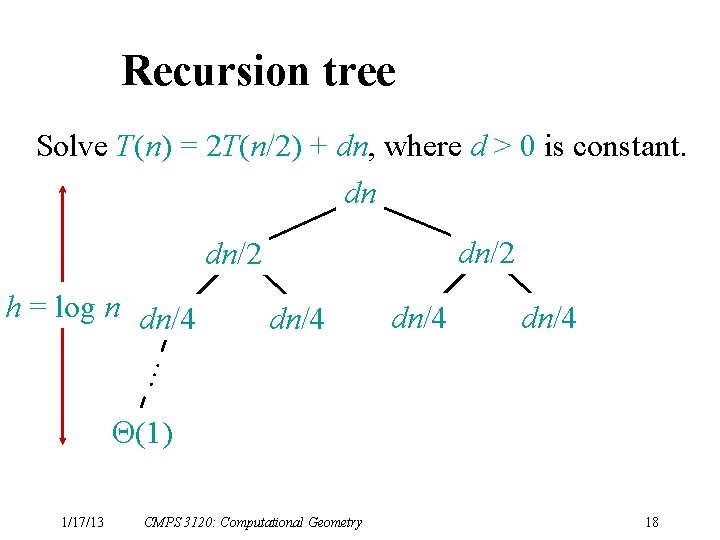
Recursion tree Solve T(n) = 2 T(n/2) + dn, where d > 0 is constant. dn dn/2 dn/4 … dn/4 (1) 1/17/13 CMPS 3120: Computational Geometry 17

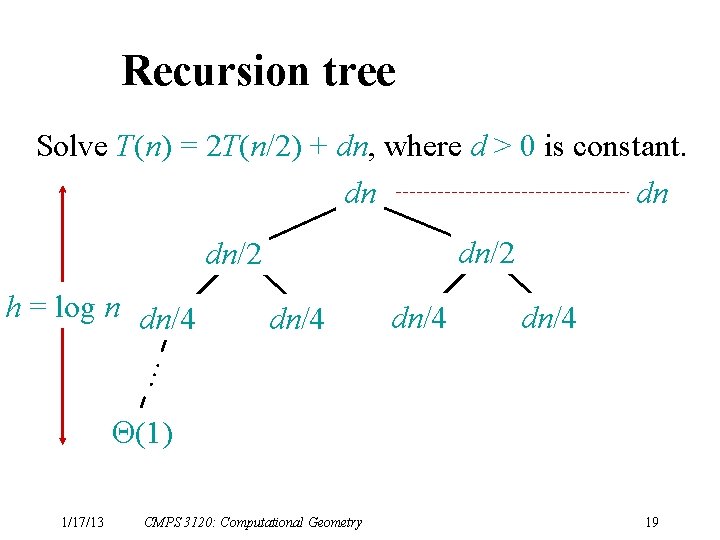
Recursion tree Solve T(n) = 2 T(n/2) + dn, where d > 0 is constant. dn dn/2 dn/4 … h = log n dn/4 (1) 1/17/13 CMPS 3120: Computational Geometry 18

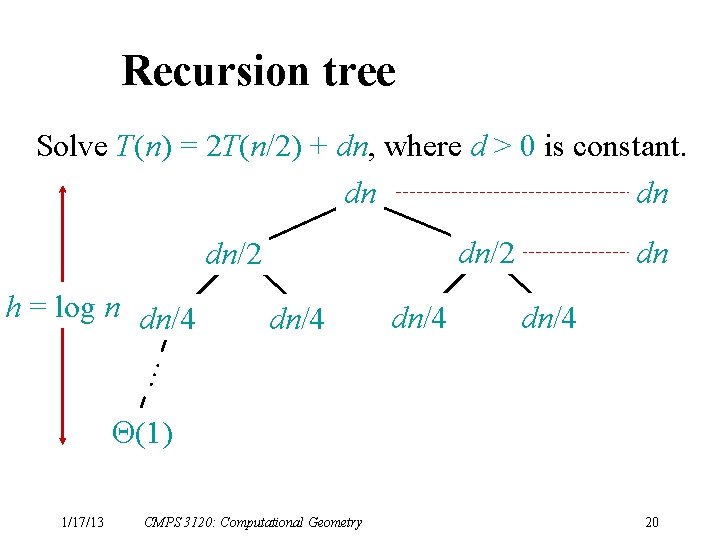
Recursion tree Solve T(n) = 2 T(n/2) + dn, where d > 0 is constant. dn dn dn/2 dn/4 … h = log n dn/4 (1) 1/17/13 CMPS 3120: Computational Geometry 19

Recursion tree Solve T(n) = 2 T(n/2) + dn, where d > 0 is constant. dn dn dn/2 dn/4 … h = log n dn/4 dn (1) 1/17/13 CMPS 3120: Computational Geometry 20

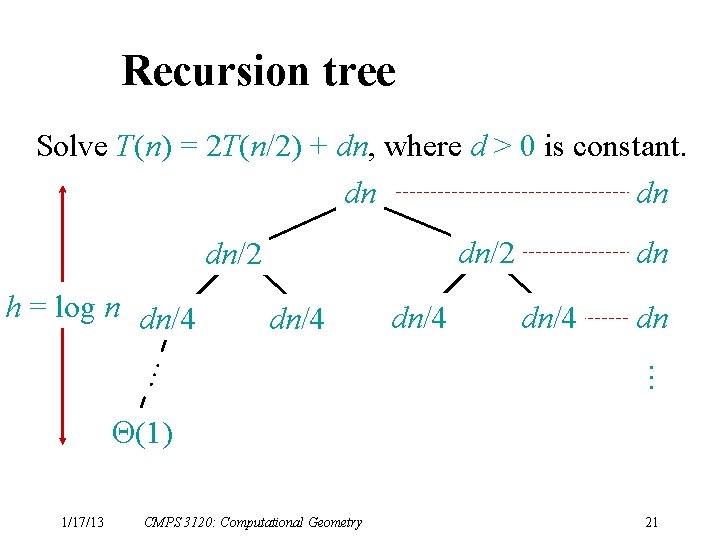
Recursion tree Solve T(n) = 2 T(n/2) + dn, where d > 0 is constant. dn dn dn/4 … h = log n dn/4 dn … dn/2 (1) 1/17/13 CMPS 3120: Computational Geometry 21

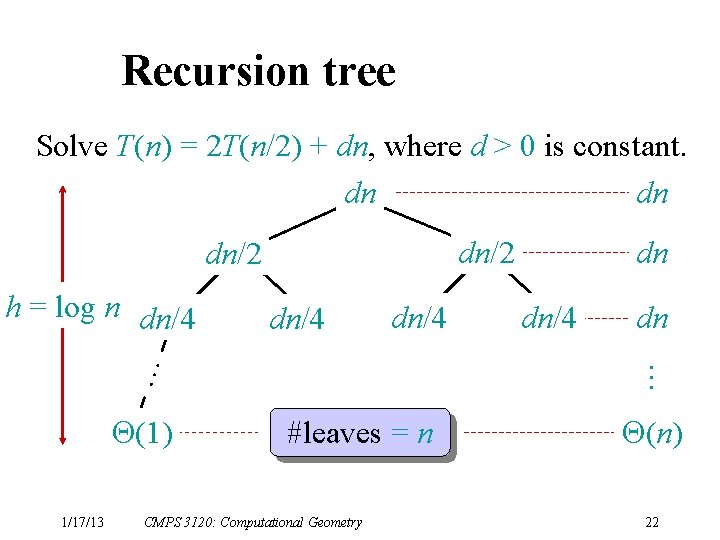
Recursion tree Solve T(n) = 2 T(n/2) + dn, where d > 0 is constant. dn dn dn/2 dn/4 (1) 1/17/13 dn/4 dn … … h = log n dn/4 dn #leaves = n CMPS 3120: Computational Geometry (n) 22

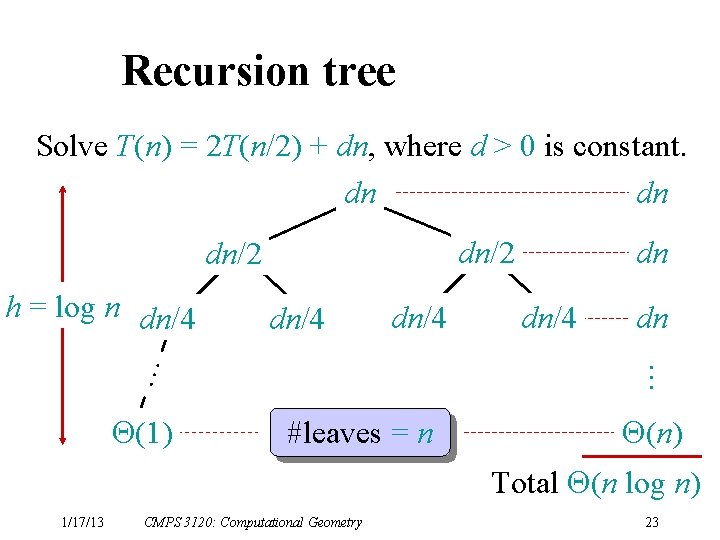
Recursion tree Solve T(n) = 2 T(n/2) + dn, where d > 0 is constant. dn dn dn/2 dn/4 (1) dn/4 dn … … h = log n dn/4 dn #leaves = n (n) Total (n log n) 1/17/13 CMPS 3120: Computational Geometry 23

The divide-and-conquer design paradigm 1. Divide the problem (instance) into subproblems. a subproblems, each of size n/b 2. Conquer the subproblems by solving them recursively. 3. Combine subproblem solutions. Runtime is f(n) 1/17/13 CMPS 3120: Computational Geometry 24

Master theorem T(n) = a T(n/b) + f (n) , where a ³ 1, b > 1, and f is asymptotically positive. CASE 1: f (n) = O(nlogba – e) T(n) = (nlogba). CASE 2: f (n) = (nlogba logkn) T(n) = (nlogba logk+1 n). CASE 3: f (n) = (nlogba + e) and a f (n/b) c f (n) T(n) = ( f (n)). Convex hull: a = 2, b = 2 nlogba = n CASE 2 (k = 0) T(n) = (n log n). 1/17/13 CMPS 3120: Computational Geometry 25

Graham’s Scan Another incremental algorithm – Compute solution by incrementally adding points – Add points in which order? • Sorted by x-coordinate • But convex hulls are cyclically ordered Break convex hull in upper and lower part upper convex hull UCH(P) lower convex hull LCH(P) 1/17/13 CMPS 3120: Computational Geometry 26

Graham’s LCH Algorithm Grahams_LCH(P): // Incrementally compute the lower convex hull of P Input: Point set P R 2 Output: A list L of vertices describing LCH(P) in counter-clockwise order O(n log n) O(n) Sort P in increasing order by x-coordinate P = {p 1, …, pn} L = {p 2, p 1} for i=3 to n while |L|>=2 and orientation(L. second(), L. first(), pi, ) <= 0 // no left turn delete first element from L Append pi to the front of L • Each element is appended only once, and hence only deleted at most once the for-loop takes O(n) time • O(n log n) time total 1/17/13 CMPS 3120: Computational Geometry 27

Lower Bound • Comparison-based sorting of n elements takes (n log n) time. • How can we use this lower bound to show a lower bound for the computation of the convex hull of n points in R 2? 1/17/13 CMPS 3120: Computational Geometry 28

Decision-tree model A decision tree models the execution of any comparison sorting algorithm: • One tree per input size n. • The tree contains all possible comparisons (= if-branches) that could be executed for any input of size n. • The tree contains all comparisons along all possible instruction traces (= control flows) for all inputs of size n. • For one input, only one path to a leaf is executed. • Running time = length of the path taken. • Worst-case running time = height of tree. 29

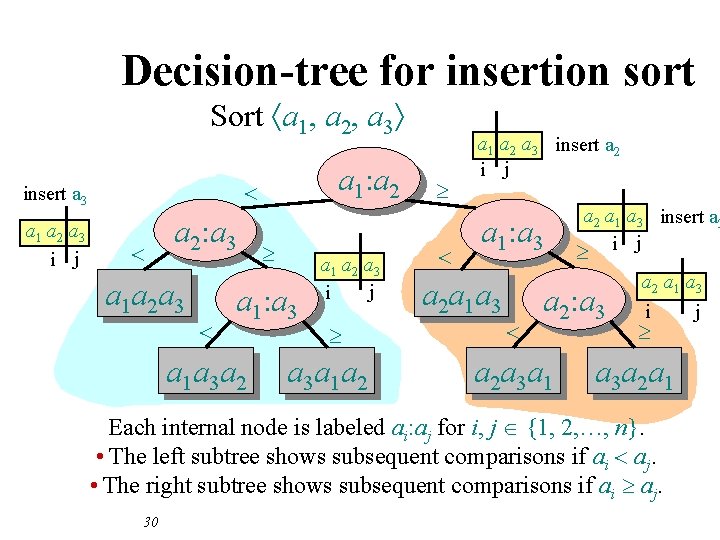
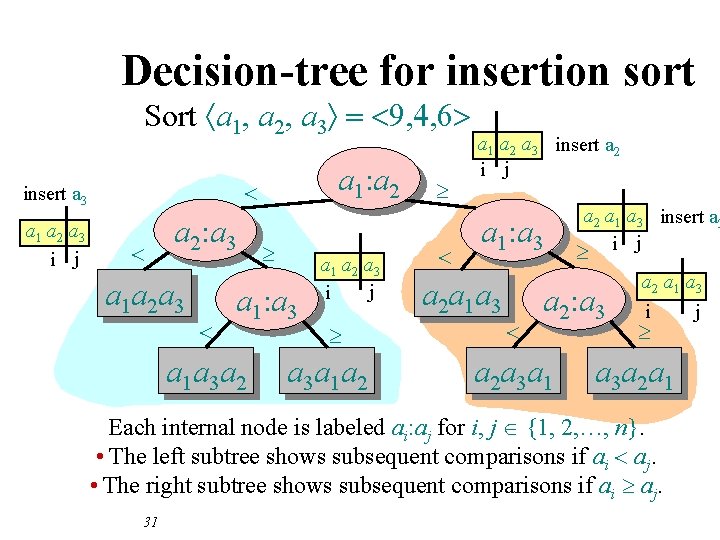
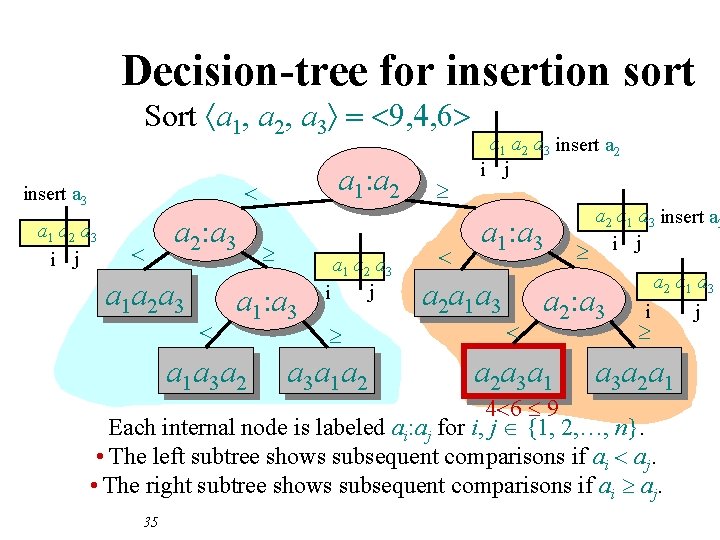
Decision-tree for insertion sort Sort áa 1, a 2, a 3ñ a 1 a 2 a 3 i j a 1: a 2 < insert a 3 < a 2: a 3 a 1 a 2 a 3 < ³ a 1: a 3 a 1 a 3 a 2 a 1 a 2 a 3 j i ³ a 3 a 1 a 2 ³ < a 1 a 2 a 3 insert a 2 i j a 1: a 3 a 2 a 1 a 3 < a 2 a 1 a 3 insert a 3 ³ i j a 2: a 3 a 2 a 3 a 1 a 2 a 1 a 3 j i ³ a 3 a 2 a 1 Each internal node is labeled ai: aj for i, j {1, 2, …, n}. • The left subtree shows subsequent comparisons if ai < aj. • The right subtree shows subsequent comparisons if ai ³ aj. 30

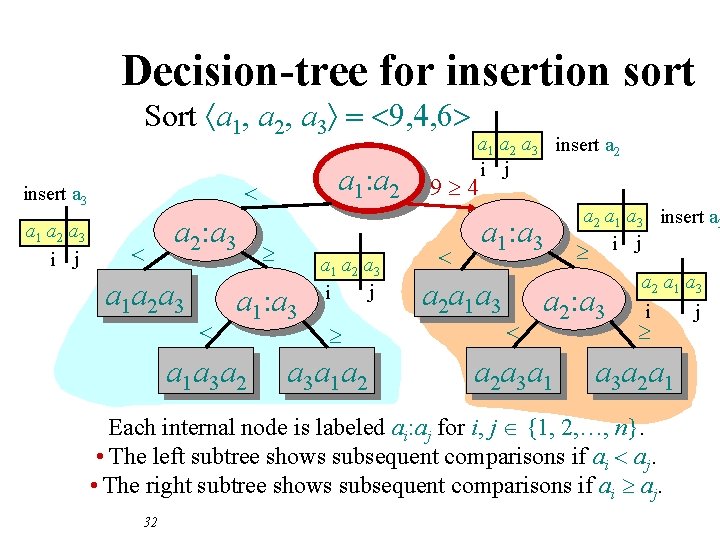
Decision-tree for insertion sort Sort áa 1, a 2, a 3ñ = <9, 4, 6> a 1 a 2 a 3 i j a 1: a 2 < insert a 3 < a 2: a 3 a 1 a 2 a 3 < ³ a 1: a 3 a 1 a 3 a 2 a 1 a 2 a 3 j i ³ a 3 a 1 a 2 ³ < a 1 a 2 a 3 insert a 2 i j a 1: a 3 a 2 a 1 a 3 < a 2 a 1 a 3 insert a 3 ³ i j a 2: a 3 a 2 a 3 a 1 a 2 a 1 a 3 j i ³ a 3 a 2 a 1 Each internal node is labeled ai: aj for i, j {1, 2, …, n}. • The left subtree shows subsequent comparisons if ai < aj. • The right subtree shows subsequent comparisons if ai ³ aj. 31

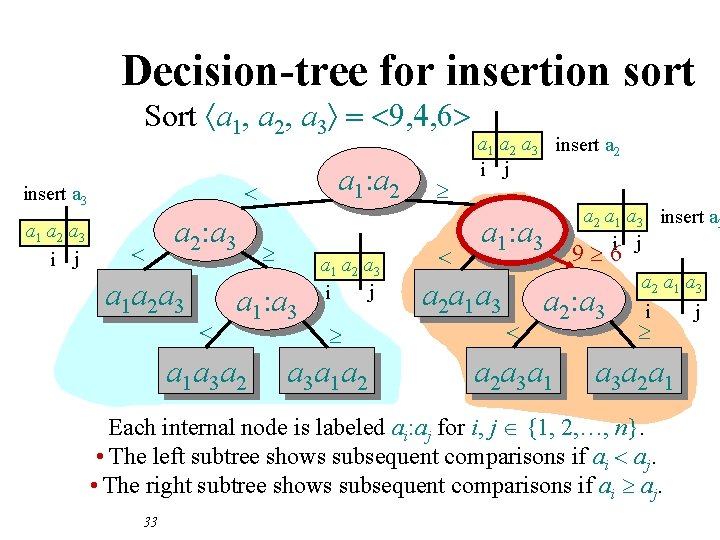
Decision-tree for insertion sort Sort áa 1, a 2, a 3ñ = <9, 4, 6> a 1 a 2 a 3 i j a 1: a 2 < insert a 3 < a 2: a 3 a 1 a 2 a 3 < ³ a 1: a 3 a 1 a 3 a 2 a 1 a 2 a 3 j i ³ a 3 a 1 a 2 a 1 a 2 a 3 insert a 2 i j 9³ 4 < a 1: a 3 a 2 a 1 a 3 < a 2 a 1 a 3 insert a 3 ³ i j a 2: a 3 a 2 a 3 a 1 a 2 a 1 a 3 j i ³ a 3 a 2 a 1 Each internal node is labeled ai: aj for i, j {1, 2, …, n}. • The left subtree shows subsequent comparisons if ai < aj. • The right subtree shows subsequent comparisons if ai ³ aj. 32

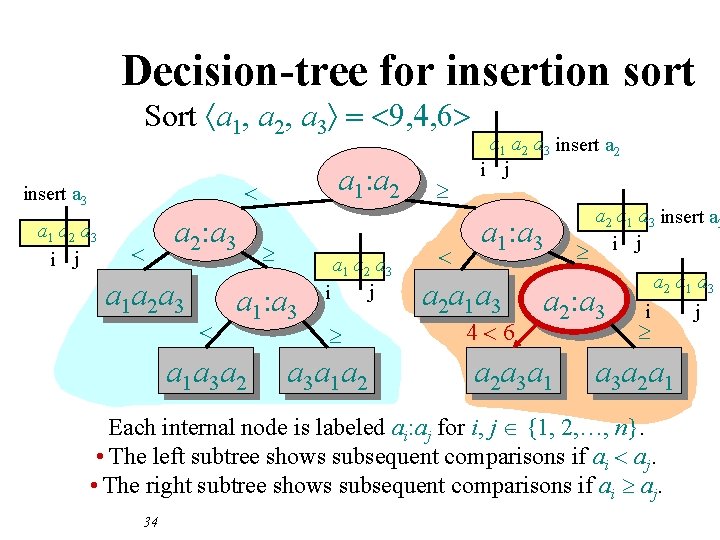
Decision-tree for insertion sort Sort áa 1, a 2, a 3ñ = <9, 4, 6> a 1 a 2 a 3 i j a 1: a 2 < insert a 3 < a 2: a 3 a 1 a 2 a 3 < ³ a 1: a 3 a 1 a 3 a 2 a 1 a 2 a 3 j i ³ a 3 a 1 a 2 ³ < a 1 a 2 a 3 insert a 2 i j a 1: a 3 a 2 a 1 a 3 < a 2 a 1 a 3 insert a 3 i j 9³ 6 a 2: a 3 a 2 a 3 a 1 a 2 a 1 a 3 j i ³ a 3 a 2 a 1 Each internal node is labeled ai: aj for i, j {1, 2, …, n}. • The left subtree shows subsequent comparisons if ai < aj. • The right subtree shows subsequent comparisons if ai ³ aj. 33

Decision-tree for insertion sort Sort áa 1, a 2, a 3ñ = <9, 4, 6> a 1: a 2 < insert a 3 a 1 a 2 a 3 i j < a 2: a 3 a 1 a 2 a 3 < ³ a 1: a 3 a 1 a 3 a 2 a 1 a 2 a 3 j i ³ a 3 a 1 a 2 ³ < a 1 a 2 a 3 insert a 2 i j a 1: a 3 a 2 a 1 a 3 4<6 ³ a 2 a 1 a 3 insert a 3 i j a 2: a 3 a 2 a 3 a 1 a 2 a 1 a 3 j i ³ a 3 a 2 a 1 Each internal node is labeled ai: aj for i, j {1, 2, …, n}. • The left subtree shows subsequent comparisons if ai < aj. • The right subtree shows subsequent comparisons if ai ³ aj. 34

Decision-tree for insertion sort Sort áa 1, a 2, a 3ñ = <9, 4, 6> a 1: a 2 < insert a 3 a 1 a 2 a 3 i j < a 2: a 3 a 1 a 2 a 3 < ³ a 1: a 3 a 1 a 3 a 2 a 1 a 2 a 3 j i ³ a 3 a 1 a 2 ³ < a 1 a 2 a 3 insert a 2 i j a 1: a 3 a 2 a 1 a 3 < ³ a 2 a 1 a 3 insert a 3 i j a 2: a 3 a 2 a 3 a 1 a 2 a 1 a 3 j i ³ a 3 a 2 a 1 4<6 9 Each internal node is labeled ai: aj for i, j {1, 2, …, n}. • The left subtree shows subsequent comparisons if ai < aj. • The right subtree shows subsequent comparisons if ai ³ aj. 35

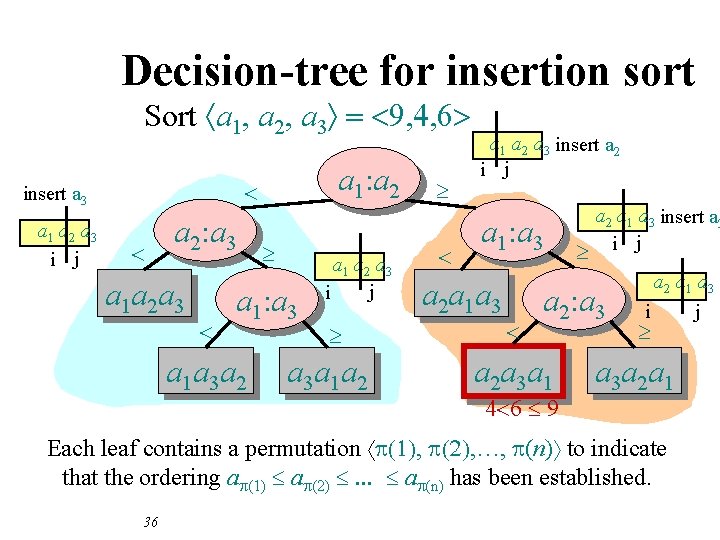
Decision-tree for insertion sort Sort áa 1, a 2, a 3ñ = <9, 4, 6> a 1 a 2 a 3 i j a 1: a 2 < insert a 3 < a 2: a 3 a 1 a 2 a 3 < ³ a 1: a 3 a 1 a 3 a 2 a 1 a 2 a 3 j i ³ a 3 a 1 a 2 ³ < a 1 a 2 a 3 insert a 2 i j a 1: a 3 a 2 a 1 a 3 < ³ a 2 a 1 a 3 insert a 3 i j a 2: a 3 a 2 a 3 a 1 4<6 9 a 2 a 1 a 3 j i ³ a 3 a 2 a 1 Each leaf contains a permutation áp(1), p(2), …, p(n)ñ to indicate that the ordering ap(1) ap(2) . . . ap(n) has been established. 36

Lower bound for comparison sorting Theorem. Any decision tree that can sort n elements must have height (n log n). Proof. The tree must contain ³ n! leaves, since there are n! possible permutations. A height-h binary tree has 2 h leaves. Thus, n! 2 h. h ³ log(n!) (log is mono. increasing) ³ log ((n/2) = n/2 log n/2 h (n log n). 37

Lower Bound • Comparison-based sorting of n elements takes (n log n) time. • How can we use this lower bound to show a lower bound for the computation of the convex hull of n points in R 2? • Devise a sorting algorithm which uses the convex hull and otherwise only linear-time operations Since this is a comparison-based sorting algorithm, the lower bound (n log n) applies Since all other operations need linear time, the convex hull algorithm has to take (n log n) time 1/17/13 CMPS 3120: Computational Geometry 38

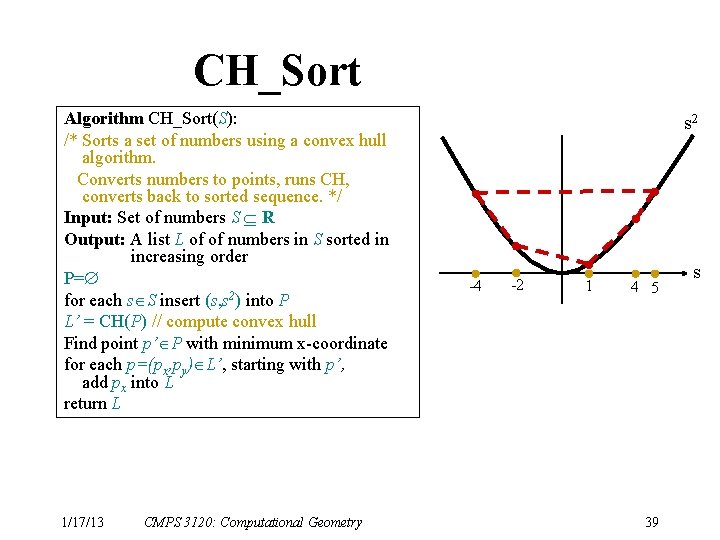
CH_Sort Algorithm CH_Sort(S): /* Sorts a set of numbers using a convex hull algorithm. Converts numbers to points, runs CH, converts back to sorted sequence. */ Input: Set of numbers S R Output: A list L of of numbers in S sorted in increasing order P= for each s S insert (s, s 2) into P L’ = CH(P) // compute convex hull Find point p’ P with minimum x-coordinate for each p=(px, py) L’, starting with p’, add px into L return L 1/17/13 CMPS 3120: Computational Geometry s 2 -4 -2 1 4 5 39 s

Convex Hull Summary • • • Brute force algorithm: Jarvis’ march (gift wrapping): Incremental insertion: Divide-and-conquer: Graham’s scan: Lower bound: 1/17/13 CMPS 3120: Computational Geometry O(n 3) O(nh) O(n log n) 40