Spring Board Geometry Circles What is a Circle

Spring Board Geometry – Circles

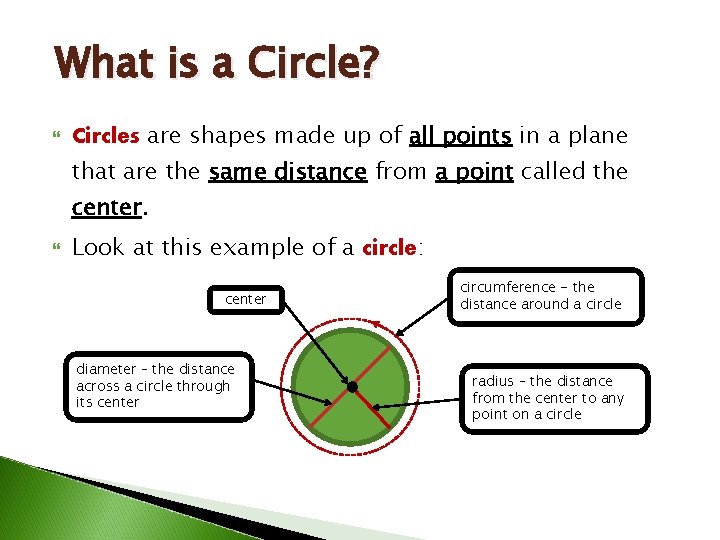
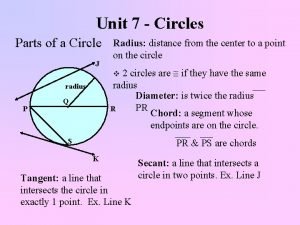
What is a Circle? Circles are shapes made up of all points in a plane that are the same distance from a point called the center. Look at this example of a circle: center diameter – the distance across a circle through its center circumference - the distance around a circle radius – the distance from the center to any point on a circle

What Do You Need to Know About Circles? What is the distance around the circle? How much space is inside the circle?

What Do You Need to Know About Circles? The distance around the circle is called the circumference. The space is inside the circle is called the area.

What is Unique About Circles? The circumference of every circle is approximately three times longer than its diameter! This relationship ( from. ) is where π or pi comes

What is Unique About Circles? To find the circumference or area of a circle, you must use this relationship or the value pi. Pi ≈ 3. 14 or You may use whichever form you wish. If your problem contains multiples of seven (7), it makes sense to use the fractional form of pi.

How Do You Find Circumference? You will always be given the circle’s diameter or the radius. Your answer will be a linear measurement. The radius is always ½ of the diameter. The diameter is always radius. diameter – the distance across a circle through its center two times the radius – the distance from the center to any point on a circle

How Do You Find Circumference? The circumference formulas are found on the key of the FCAT Reference Sheet.

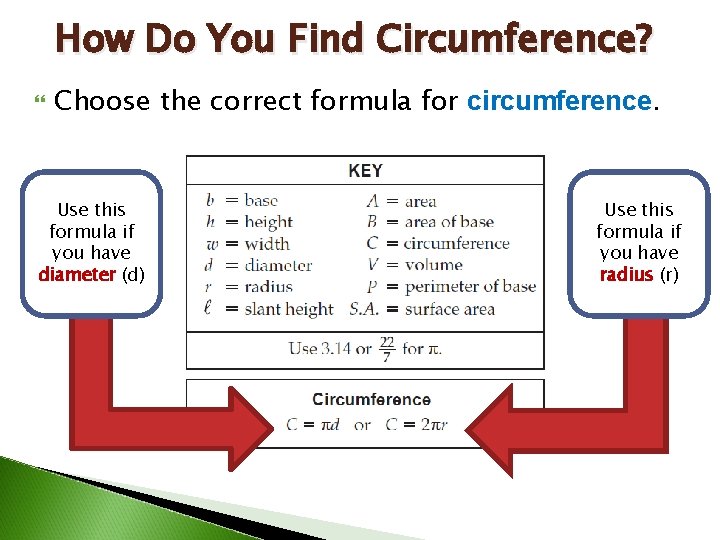
How Do You Find Circumference? Choose the correct formula for circumference. Use this formula if you have diameter (d) Use this formula if you have radius (r)

How Do You Find Circumference? Write the circumference formula exactly as it appears on the FCAT Reference Sheet. Rewrite the circumference formula substituting the values that you know. Solve one step at a time rewriting after each step. C = Πd s er et m A = 28. 26 meters 9 C = 3. 14 × 12

How Do You Find Circumference? Write the circumference formula exactly as it appears on the FCAT Reference Sheet. Rewrite the circumference formula substituting the values that you know. Solve one step at a time rewriting after each step. C = 2Πr C = 2 × 3. 14 × 12 A = 75. 36 meters

How Do You Solve for a Missing Measurement? Follow the same set of steps as before! v Write the circumference formula exactly as it appears on the FCAT Reference Sheet. v Rewrite the circumference formula substituting the values that you know. v Solve one step at a time rewriting after each step.

How Do You Solve for a Missing Measurement? Solve the following problem: v Find the diameter of a basketball hoop with a circumference of 56. 52 inches. Use 3. 14 for Π. C 56. 52 18 in. = Πd = 3. 14 × d Divide by 3. 14 on both sides to undo the multiplication! =d

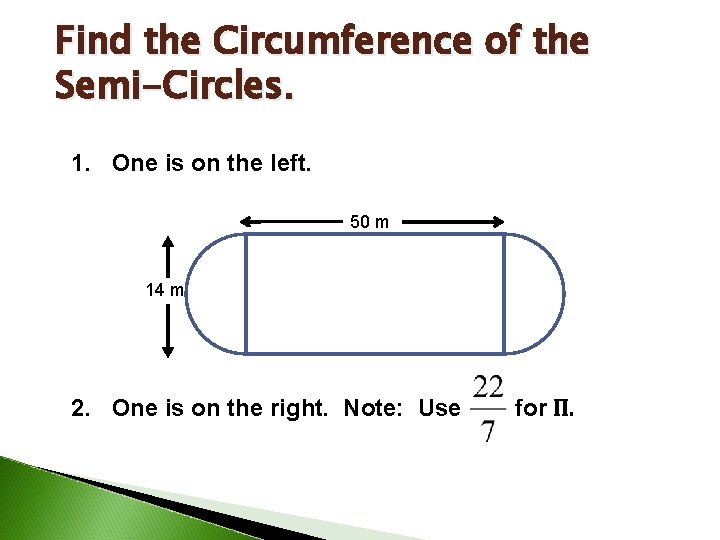
Find the Circumference of the Semi-Circles. 1. One is on the left. 50 m 14 m 2. One is on the right. Note: Use for Π.

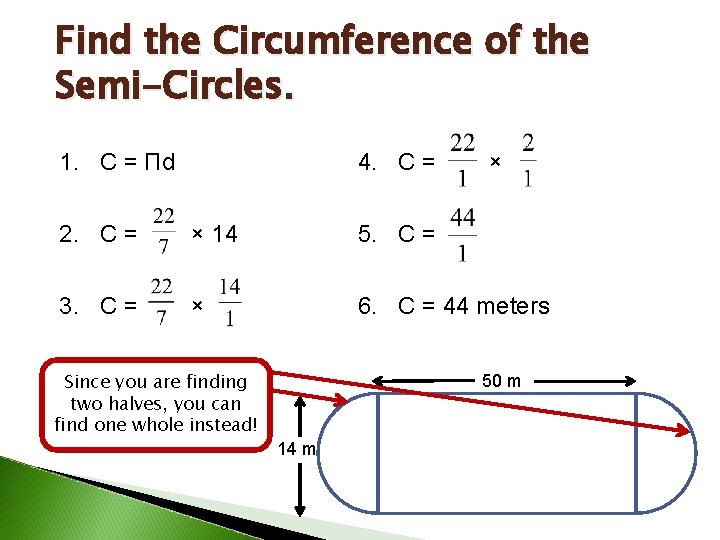
Find the Circumference of the Semi-Circles. 4. C = 1. C = Πd × 2. C = × 14 5. C = 3. C = × 6. C = 44 meters Since you are finding two halves, you can find one whole instead! 50 m 14 m

How Do You Find the Area? You will always be given the circle’s diameter, radius, or its circumference. You need to find the value of radius before you begin! ½ of the diameter or r = d ÷ 2. The radius is always The diameter is equal to circumference divided by pi or 3. 14. Or d = Sometimes you are given radius. This means less work!!

Find Area of a Circle Select the correct area formula:

Find Area of a Circle Write the area formula exactly as it appears on the FCAT Reference Sheet. Rewrite the area formula substituting the values that you know. Solve one step at a time rewriting after each step. 2 12 mm A = Πr A = 3. 14 × 12 A = 3. 14 × 144 A = 452. 16 mm 2

Find Area of a Circle Write the area formula exactly as it appears on the FCAT Reference Sheet. Rewrite the area formula substituting the values that you know. Solve one step at a time rewriting after each step. A = Πr 2 r=d÷ 2 A = 3. 14 × r r=6÷ 2 A = 3. 14 × 3 r=3 A = 3. 14 × 9 A = 28. 26 ft 2 6 feet

Find Area of a Semi-Circle Write the area formula exactly as it appears on the FCAT Reference Sheet. Rewrite the area formula substituting the values that you know. Solve one step at a time rewriting after each step. Divide your answer by 2! Note: You could also use the formula or

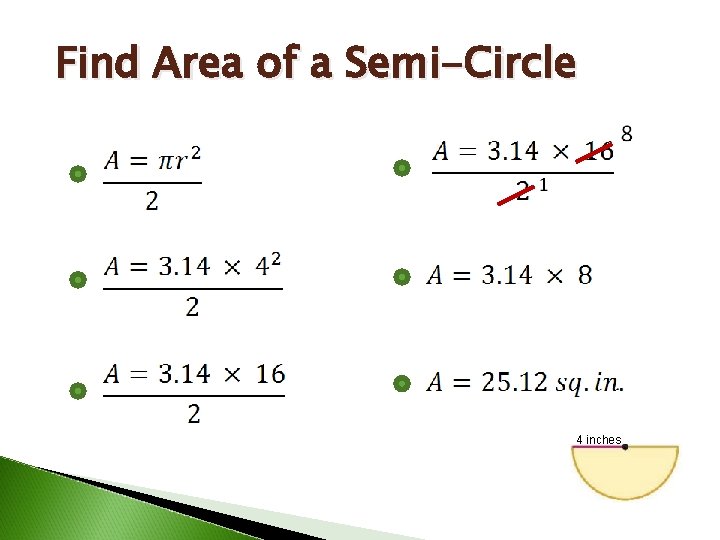
Find Area of a Semi-Circle 4 inches

Find Area of a Semi-Circle Remember to multiply by ½ or divide by 2! Choose the formula that you feel the most comfortable using. You are finding the area of one half of a circle! You can use this same method to find the circumference of one half of a circle!

Why is Area in Square Units? Remember that the shapes have two dimensions. When you multiply one measurement by another measurement you end up with square units. For Example: • Square Feet • ft 2 • Square Inches • Square Centimeters • in 2 • cm 2

Time to Practice Remember to use the FCAT Reference Sheet: