Clipping Lines Dr Scott Schaefer Why Clip n

Clipping Lines Dr. Scott Schaefer

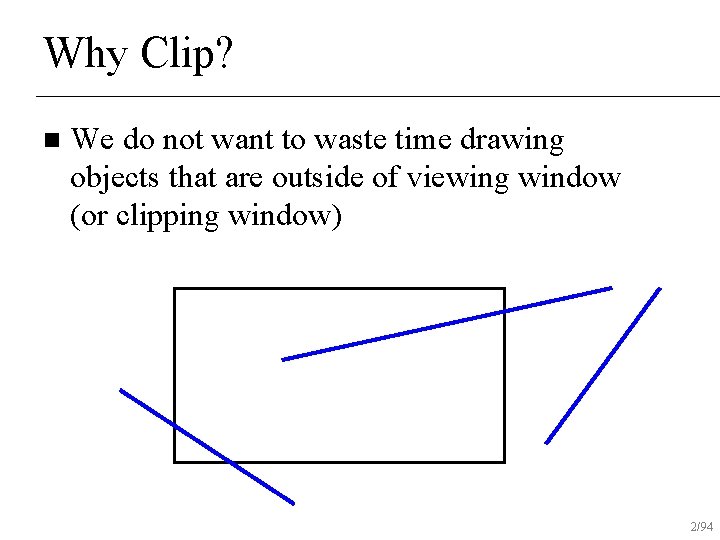
Why Clip? n We do not want to waste time drawing objects that are outside of viewing window (or clipping window) 2/94

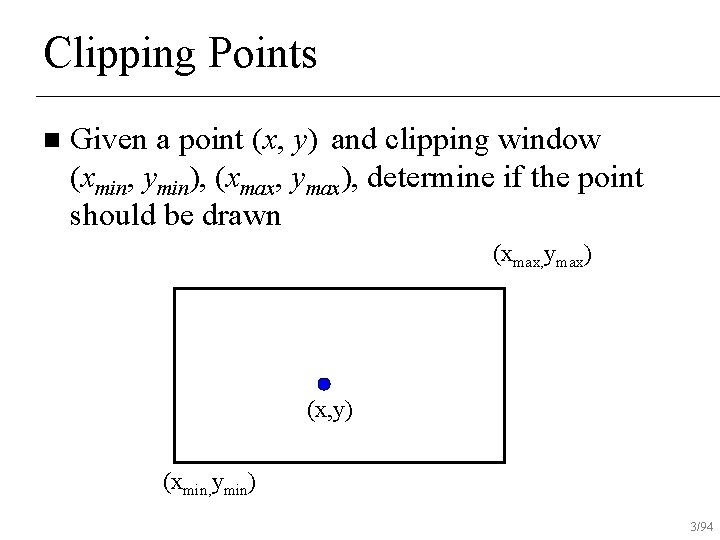
Clipping Points n Given a point (x, y) and clipping window (xmin, ymin), (xmax, ymax), determine if the point should be drawn (xmax, ymax) (x, y) (xmin, ymin) 3/94

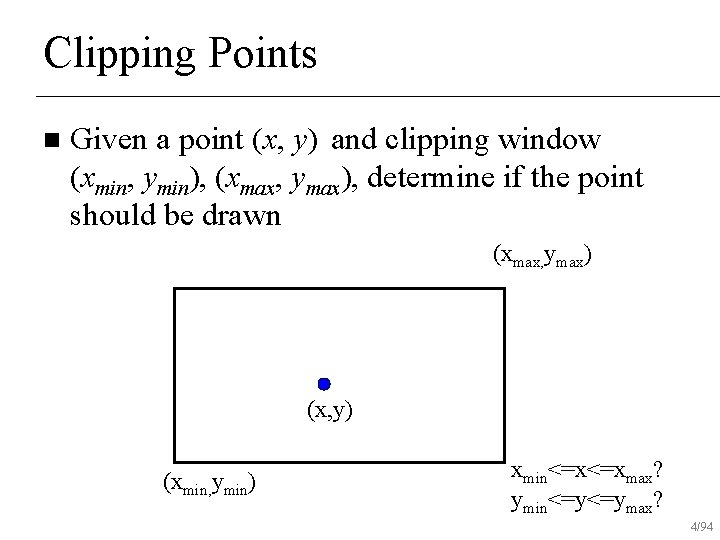
Clipping Points n Given a point (x, y) and clipping window (xmin, ymin), (xmax, ymax), determine if the point should be drawn (xmax, ymax) (x, y) (xmin, ymin) xmin<=x<=xmax? ymin<=y<=ymax? 4/94

Clipping Points n Given a point (x, y) and clipping window (xmin, ymin), (xmax, ymax), determine if the point should be drawn (xmax, ymax) (x 1, y 1) (xmin, ymin) (x 2, y 2) xmin<=x<=xmax? ymin<=y<=ymax? 5/94

Clipping Points n Given a point (x, y) and clipping window (xmin, ymin), (xmax, ymax), determine if the point should be drawn (xmax, ymax) (x 1, y 1) (xmin, ymin) (x 2, y 2) xmin<=x 1<=xmax Yes ymin<=y 1<=ymax Yes 6/94

Clipping Points n Given a point (x, y) and clipping window (xmin, ymin), (xmax, ymax), determine if the point should be drawn (xmax, ymax) (x 1, y 1) (xmin, ymin) (x 2, y 2) xmin<=x 2<=xmax No ymin<=y 2<=ymax Yes 7/94

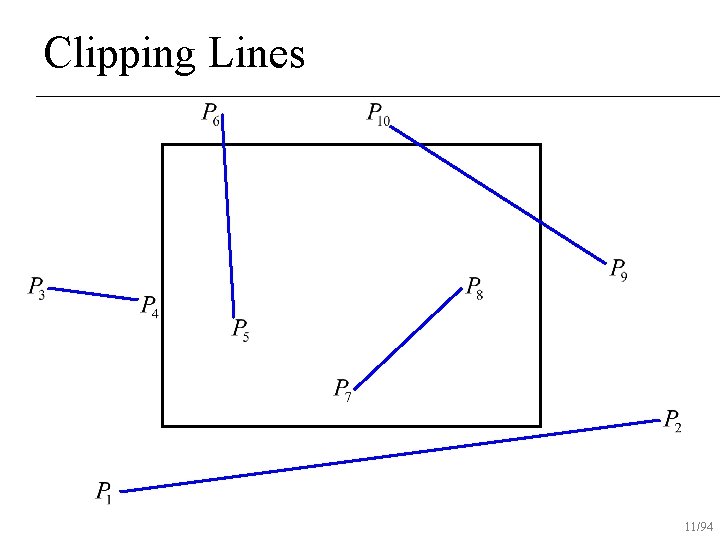
Clipping Lines 8/94

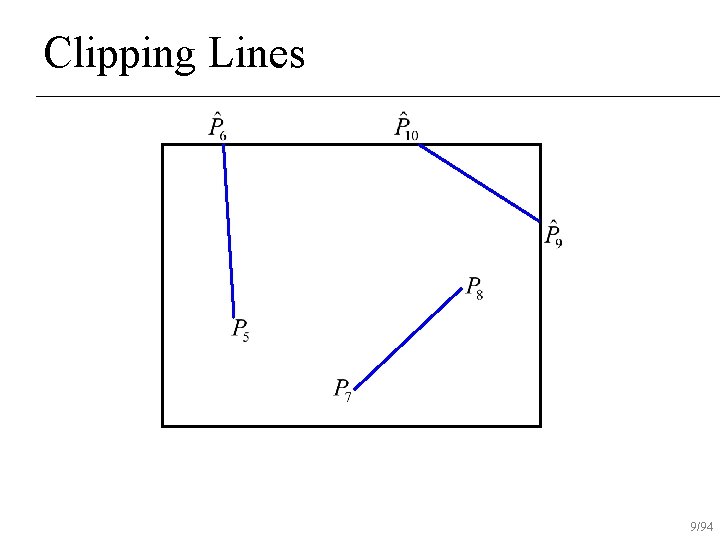
Clipping Lines 9/94

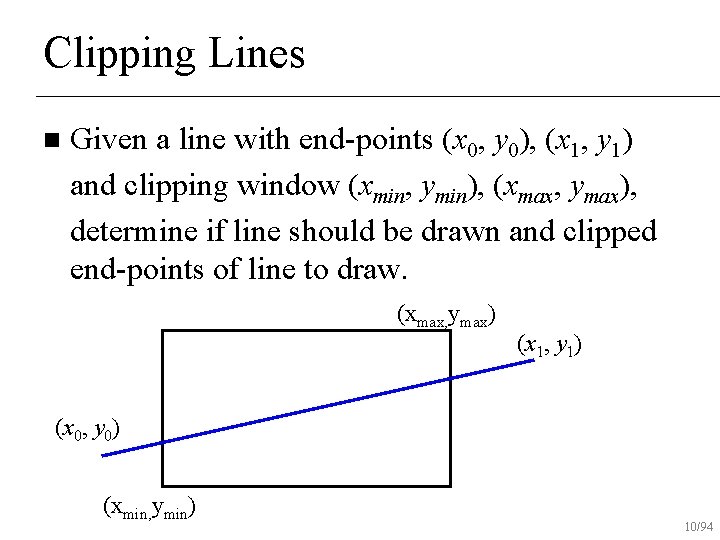
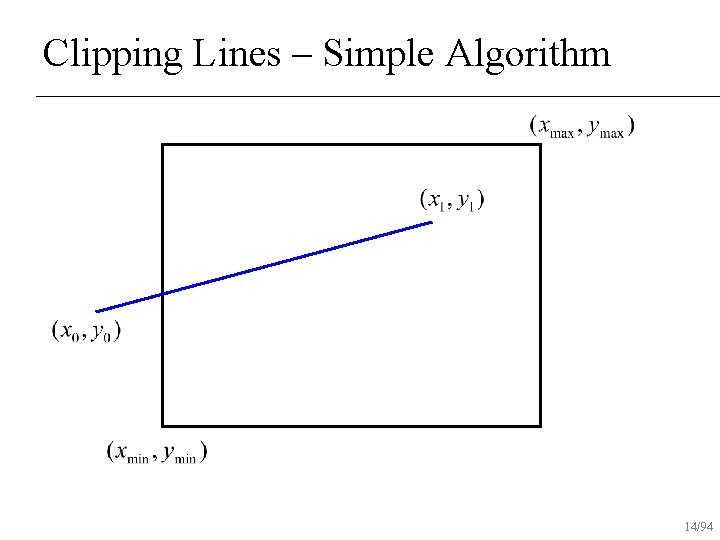
Clipping Lines n Given a line with end-points (x 0, y 0), (x 1, y 1) and clipping window (xmin, ymin), (xmax, ymax), determine if line should be drawn and clipped end-points of line to draw. (xmax, ymax) (x 1, y 1) (x 0, y 0) (xmin, ymin) 10/94

Clipping Lines 11/94

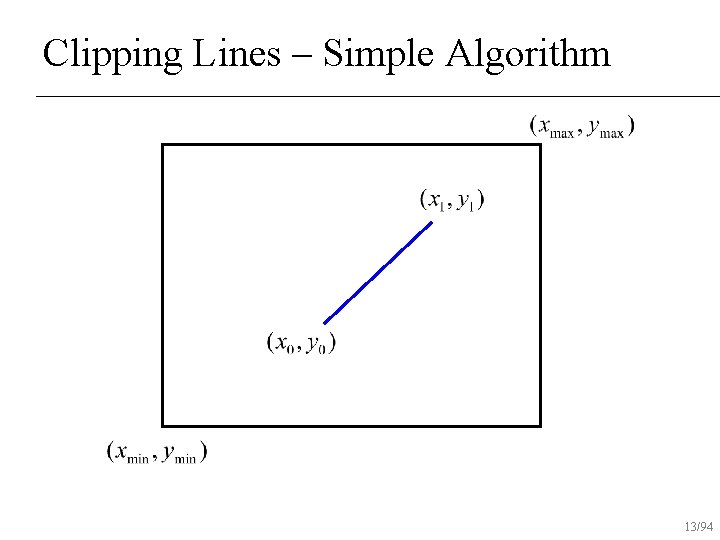
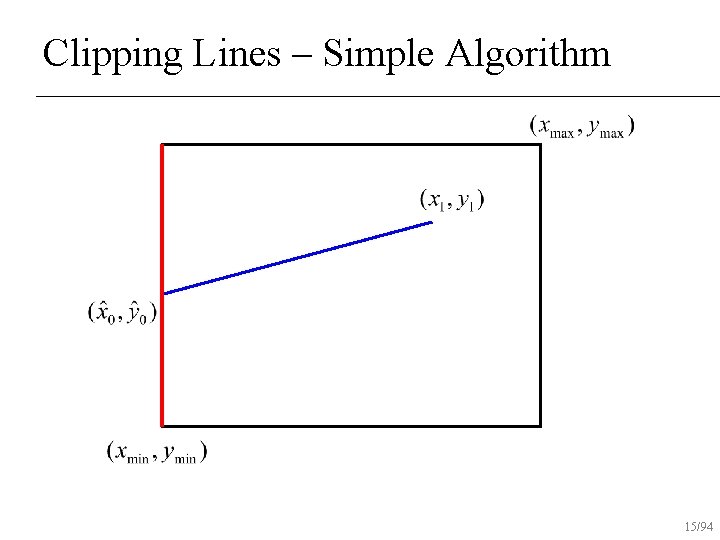
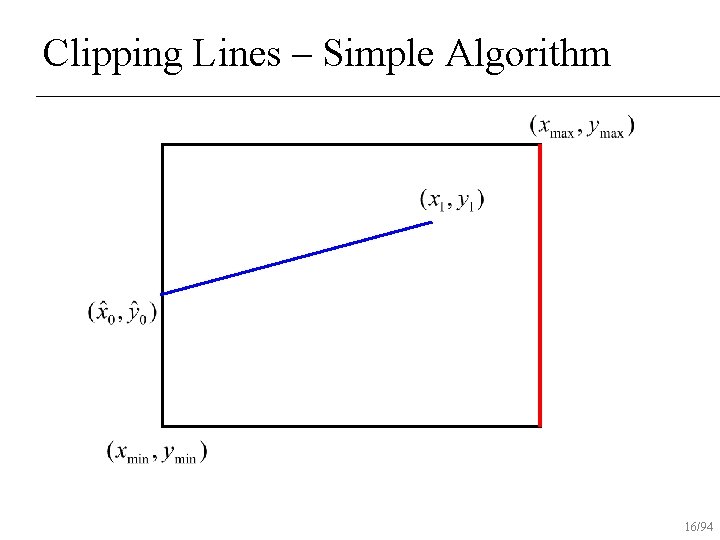
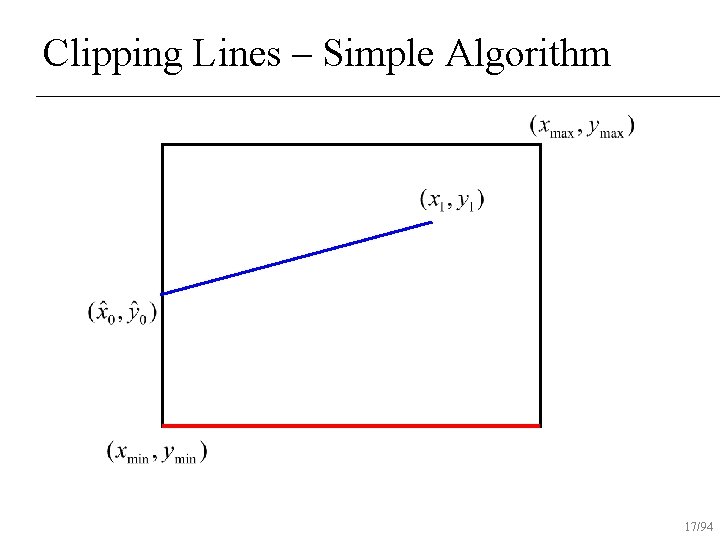
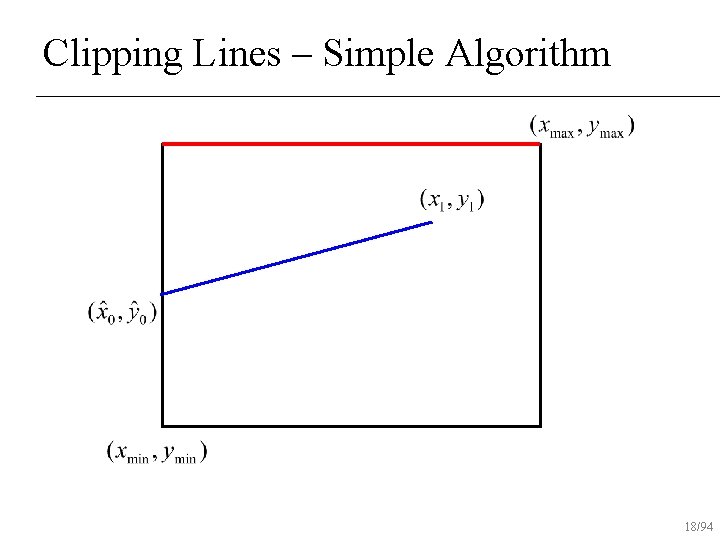
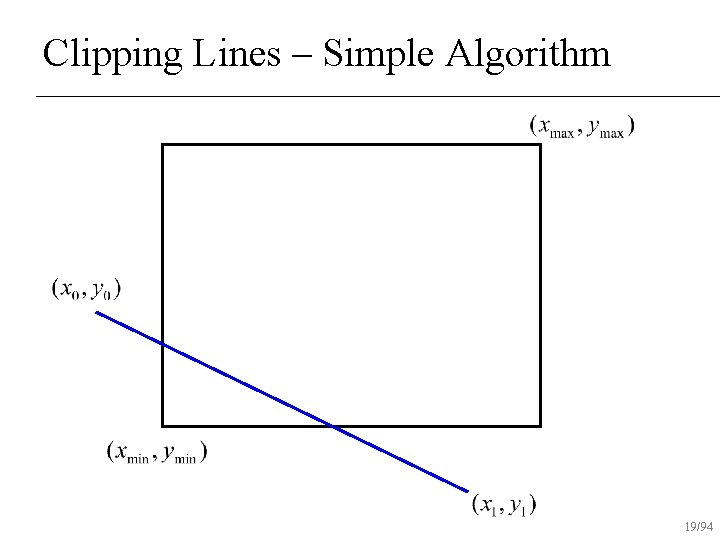
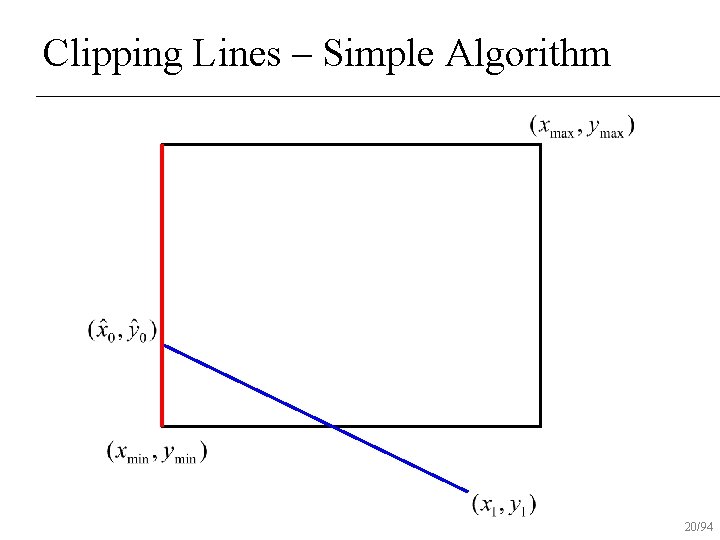
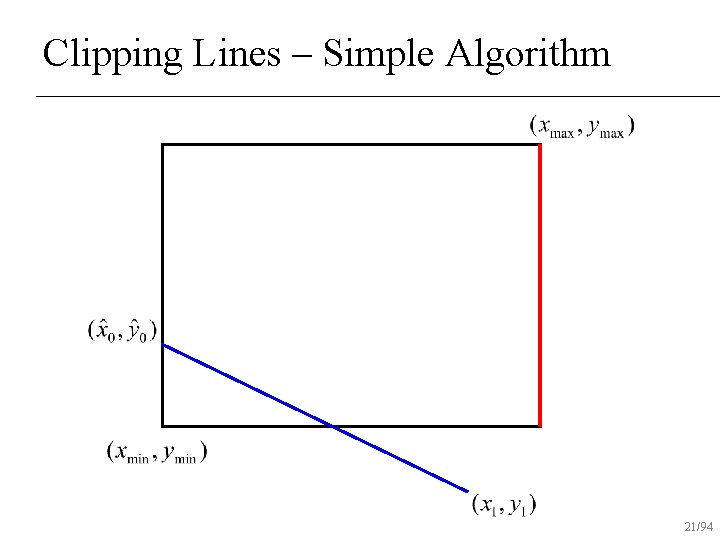
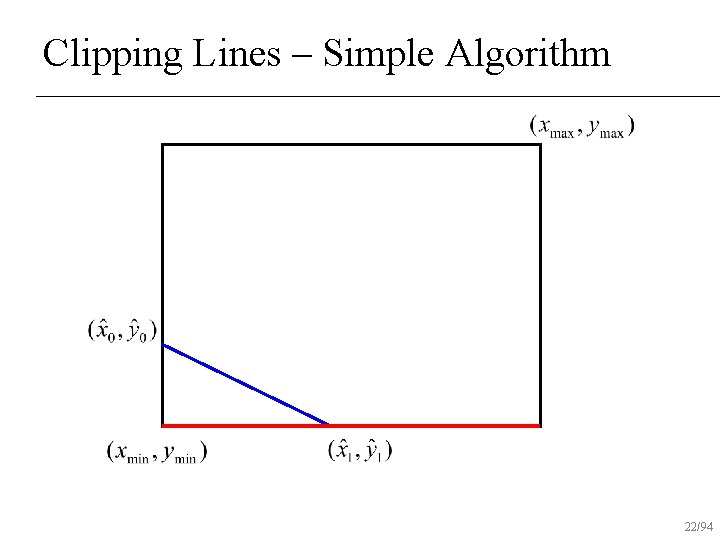
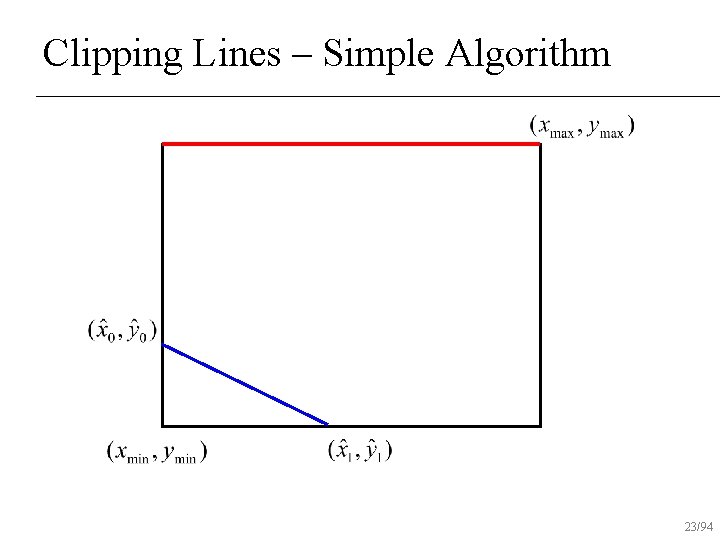
Clipping Lines – Simple Algorithm If both end-points inside rectangle, draw line n Otherwise, intersect line with all edges of rectangle clip that point and repeat test n 12/94

Clipping Lines – Simple Algorithm 13/94

Clipping Lines – Simple Algorithm 14/94

Clipping Lines – Simple Algorithm 15/94

Clipping Lines – Simple Algorithm 16/94

Clipping Lines – Simple Algorithm 17/94

Clipping Lines – Simple Algorithm 18/94

Clipping Lines – Simple Algorithm 19/94

Clipping Lines – Simple Algorithm 20/94

Clipping Lines – Simple Algorithm 21/94

Clipping Lines – Simple Algorithm 22/94

Clipping Lines – Simple Algorithm 23/94

Window Intersection (x 1, y 1), (x 2, y 2) intersect with vertical edge at xright t yintersect = y 1 + m(xright – x 1) where m=(y 2 -y 1)/(x 2 -x 1) (x 1, y 1), (x 2, y 2) intersect with horizontal edge at ybottom t xintersect = x 1 + (ybottom – y 1)/m where m=(y 2 -y 1)/(x 2 -x 1) 24/94

Clipping Lines – Simple Algorithm Lots of intersection tests makes algorithm expensive n Complicated tests to determine if intersecting rectangle n n Is there a better way? 25/94

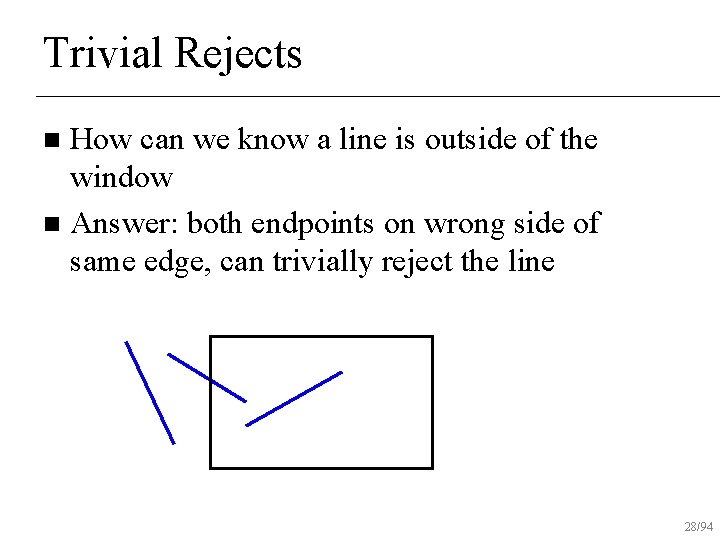
Trivial Accepts Big Optimization: trivial accepts/rejects n How can we quickly decide whether line segment is entirely inside window n Answer: test both endpoints n 26/94

Trivial Accepts Big Optimization: trivial accepts/rejects n How can we quickly decide whether line segment is entirely inside window n Answer: test both endpoints n 27/94

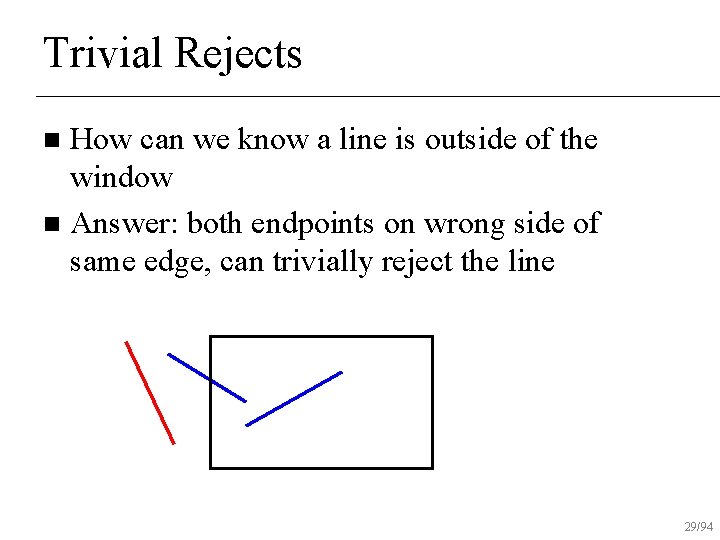
Trivial Rejects How can we know a line is outside of the window n Answer: both endpoints on wrong side of same edge, can trivially reject the line n 28/94

Trivial Rejects How can we know a line is outside of the window n Answer: both endpoints on wrong side of same edge, can trivially reject the line n 29/94

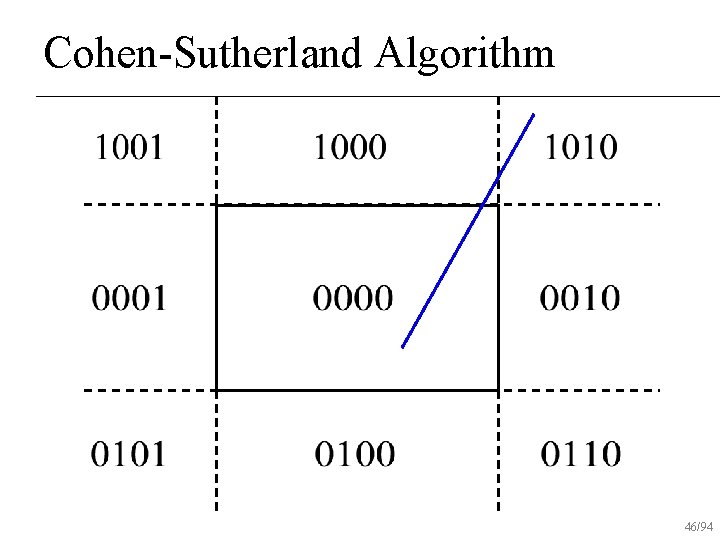
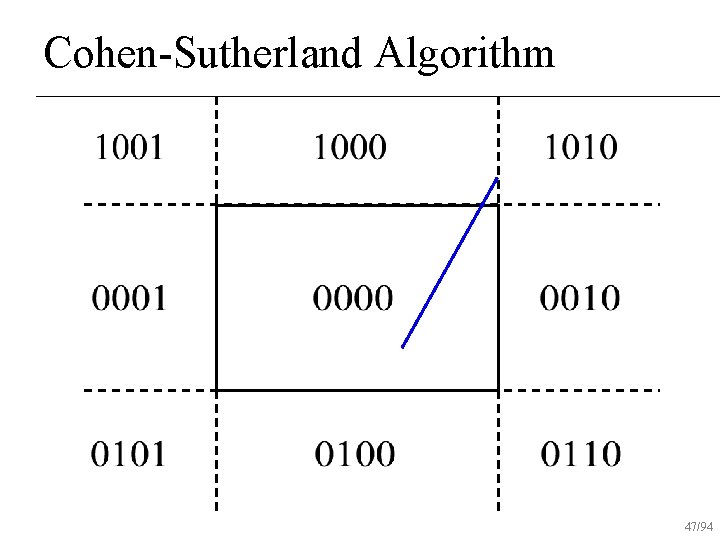
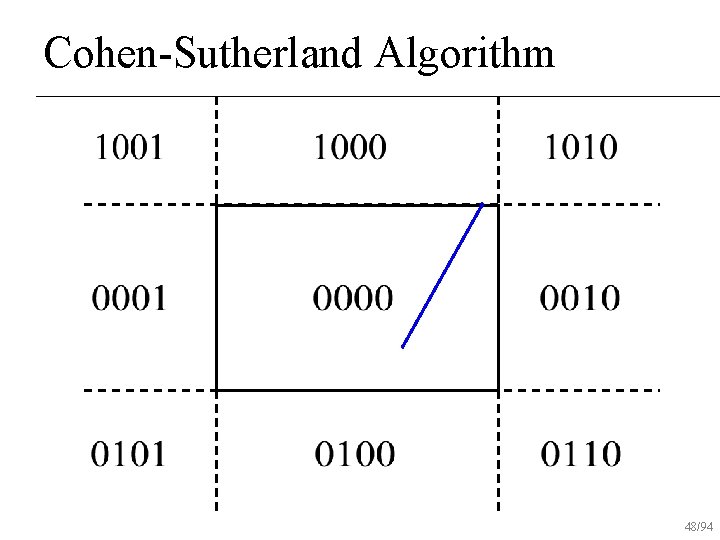
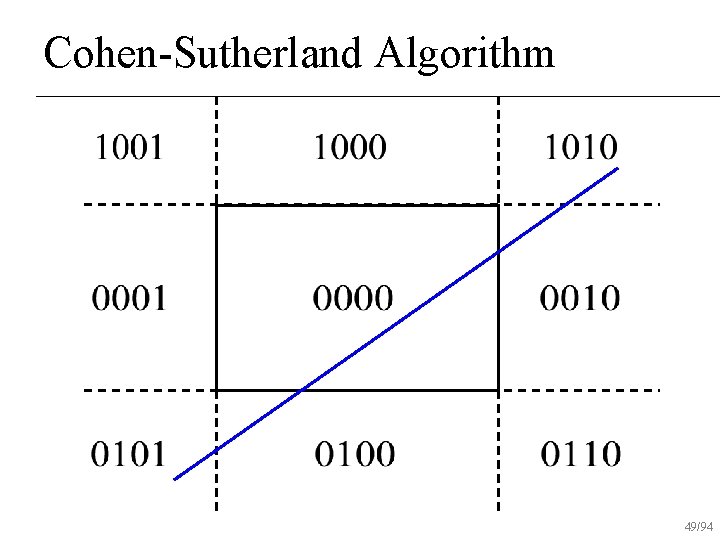
Cohen-Sutherland Algorithm Classify p 0, p 1 using region codes c 0, c 1 n If , trivially reject n If , trivially accept n Otherwise reduce to trivial cases by splitting into two segments n 30/94

Cohen-Sutherland Algorithm Every end point is assigned to a four-digit binary value, i. e. Region code n Each bit position indicates whether the point is inside or outside of a specific window edge n bit 4 bit 3 bit 2 bit 1 top bottom right left 31/94

Cohen-Sutherland Algorithm 32/94

Cohen-Sutherland Algorithm Classify p 0, p 1 using region codes c 0, c 1 n If , trivially reject n If , trivially accept n Otherwise reduce to trivial cases by splitting into two segments n 33/94

Cohen-Sutherland Algorithm Classify p 0, p 1 using region codes c 0, c 1 n If , trivially reject n If , trivially accept n Otherwise reduce to trivial cases by splitting into two segments n 34/94

Cohen-Sutherland Algorithm Classify p 0, p 1 using region codes c 0, c 1 n If , trivially reject n If , trivially accept n Otherwise reduce to trivial cases by splitting into two segments n Line is outside the window! reject 35/94

Cohen-Sutherland Algorithm Classify p 0, p 1 using region codes c 0, c 1 n If , trivially reject n If , trivially accept n Otherwise reduce to trivial cases by splitting into two segments n Line is inside the window! draw 36/94

Cohen-Sutherland Algorithm Classify p 0, p 1 using region codes c 0, c 1 n If , trivially reject n If , trivially accept n Otherwise reduce to trivial cases by splitting into two segments n 37/94

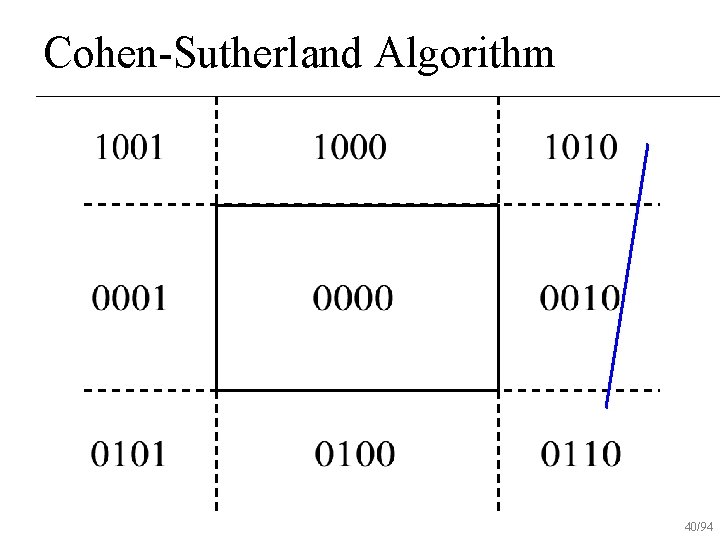
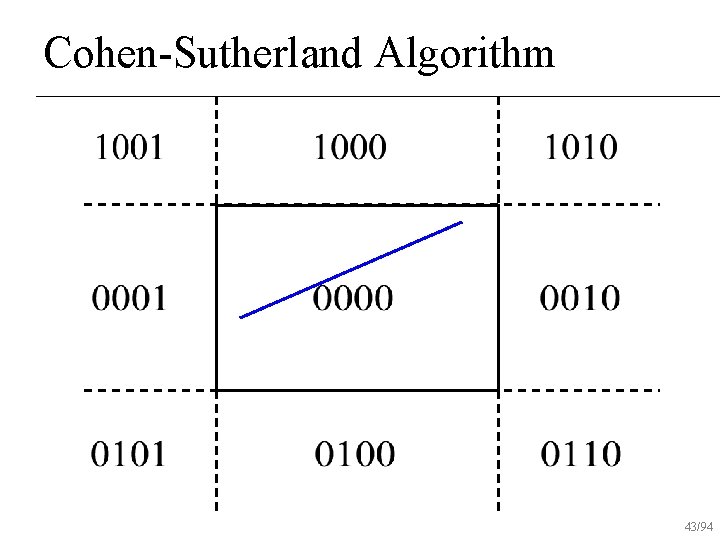
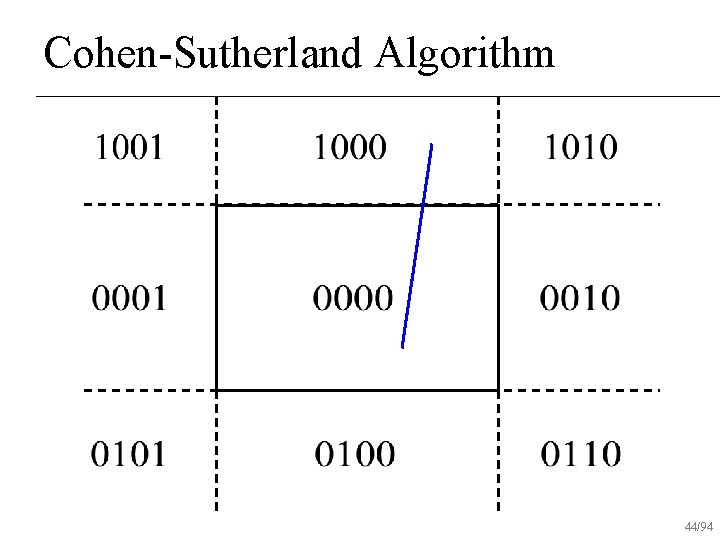
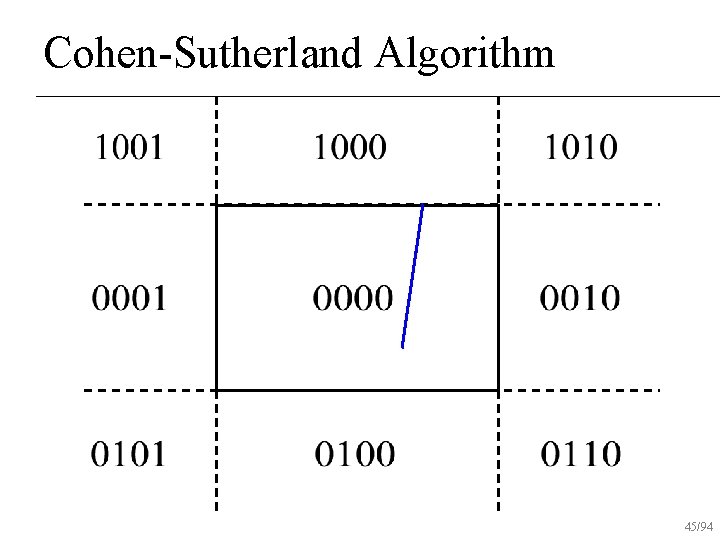
Cohen-Sutherland Algorithm 38/94

Cohen-Sutherland Algorithm 39/94

Cohen-Sutherland Algorithm 40/94

Cohen-Sutherland Algorithm 41/94

Cohen-Sutherland Algorithm 42/94

Cohen-Sutherland Algorithm 43/94

Cohen-Sutherland Algorithm 44/94

Cohen-Sutherland Algorithm 45/94

Cohen-Sutherland Algorithm 46/94

Cohen-Sutherland Algorithm 47/94

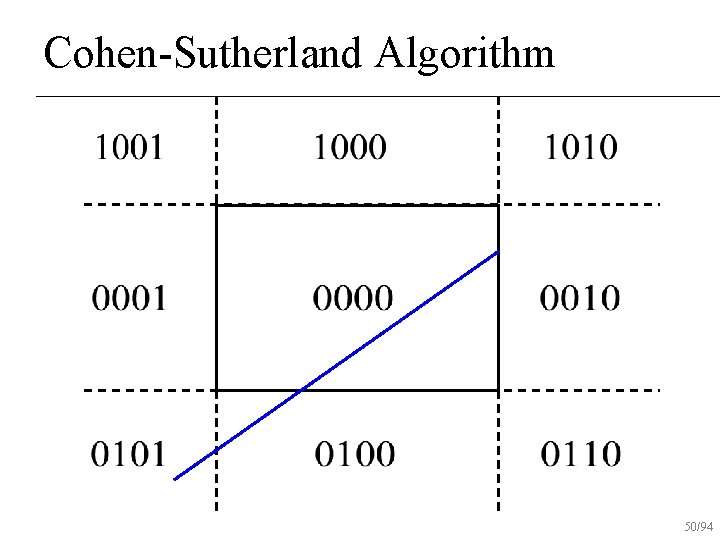
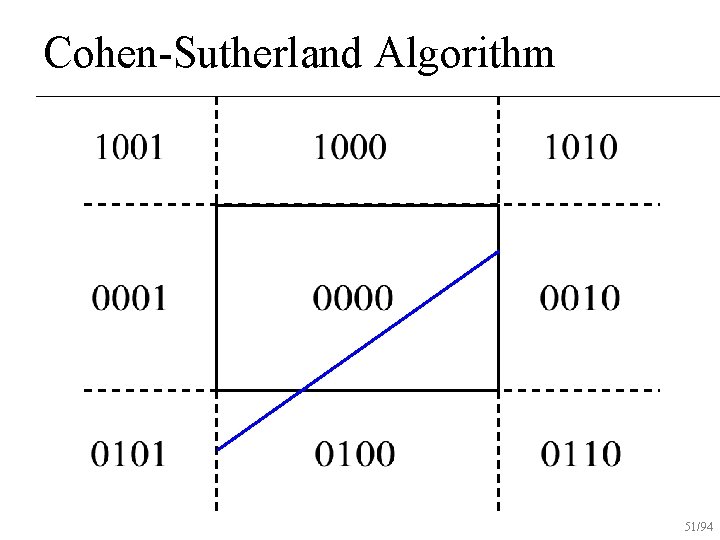
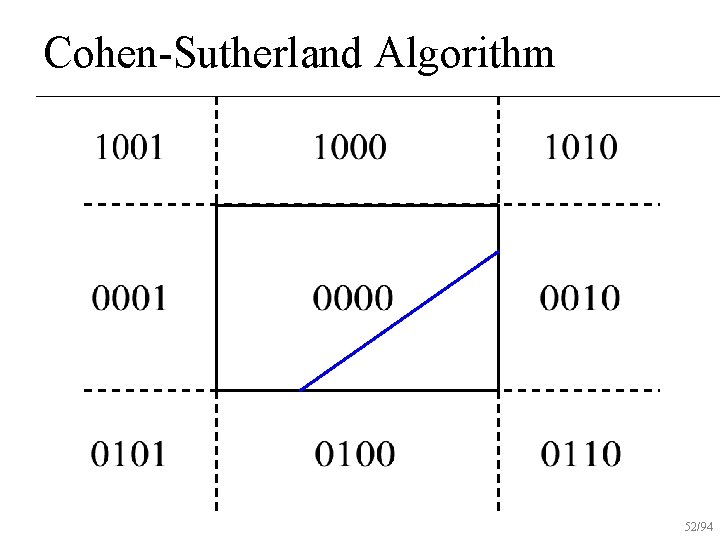
Cohen-Sutherland Algorithm 48/94

Cohen-Sutherland Algorithm 49/94

Cohen-Sutherland Algorithm 50/94

Cohen-Sutherland Algorithm 51/94

Cohen-Sutherland Algorithm 52/94

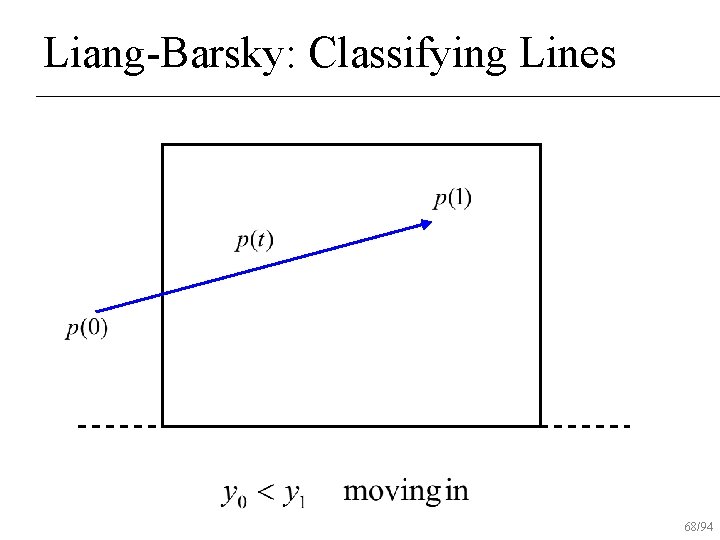
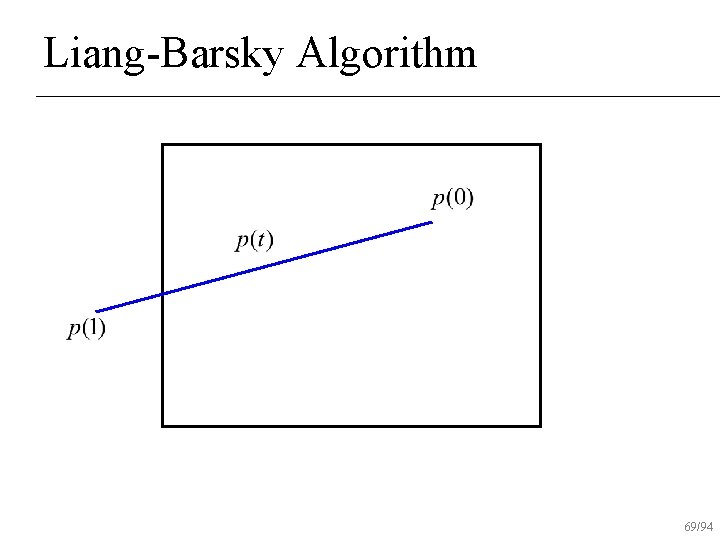
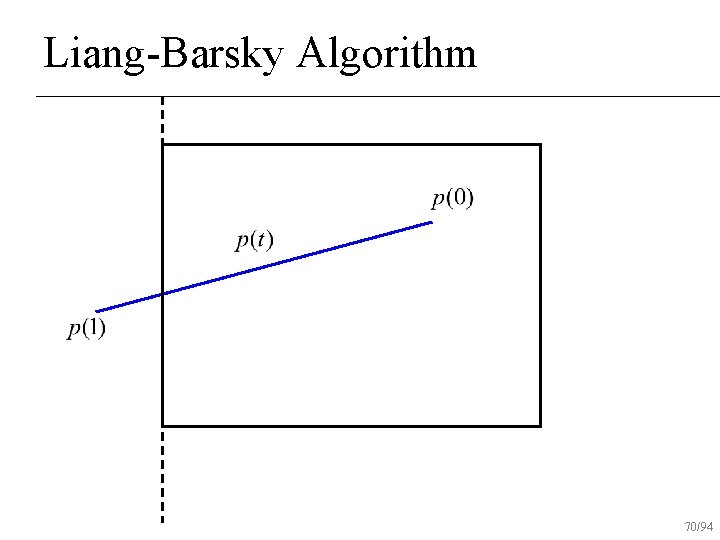
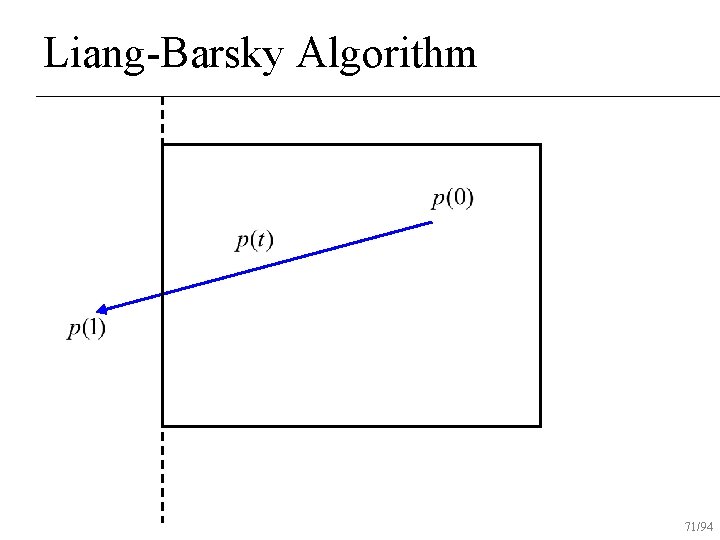
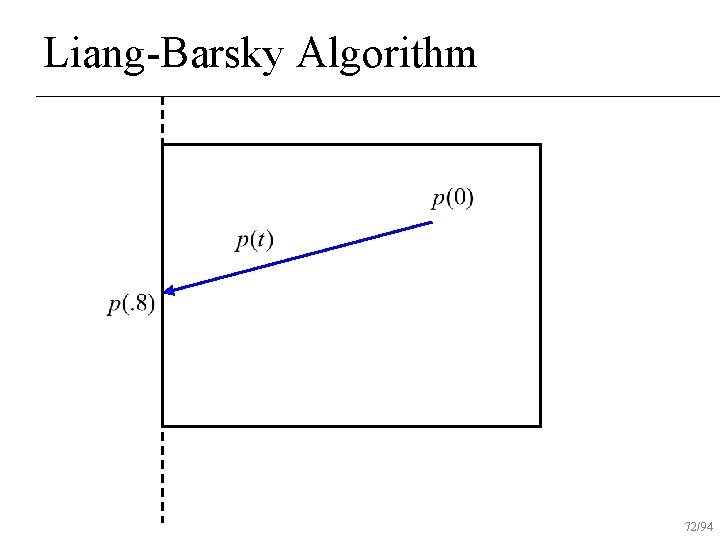
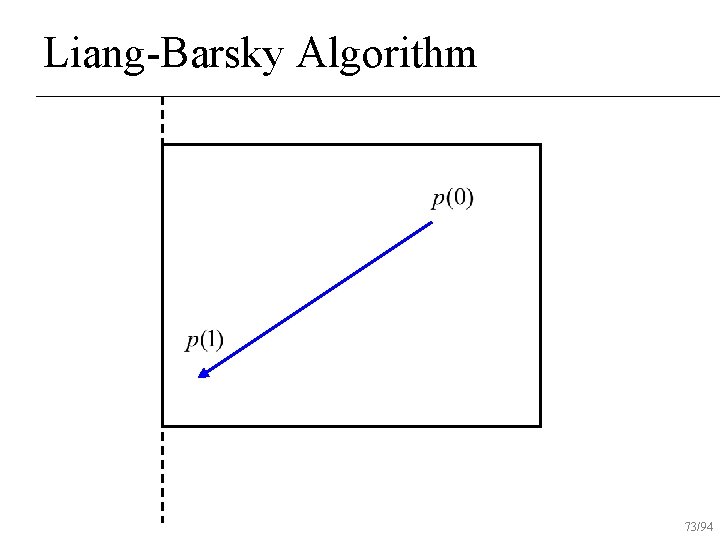
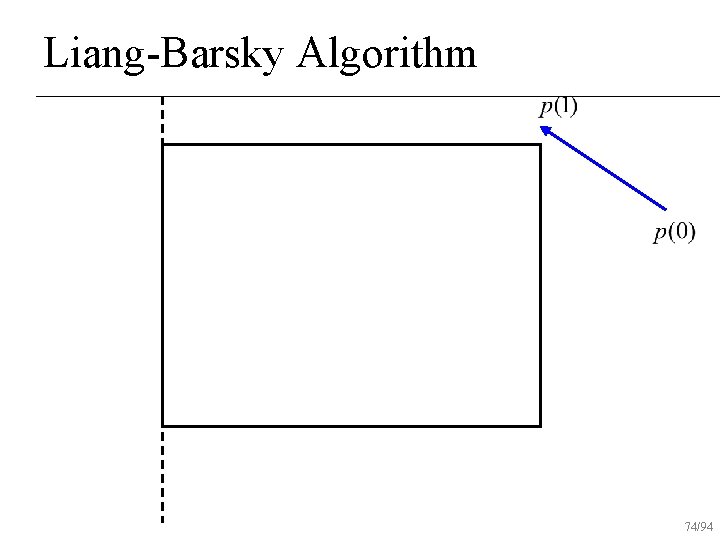
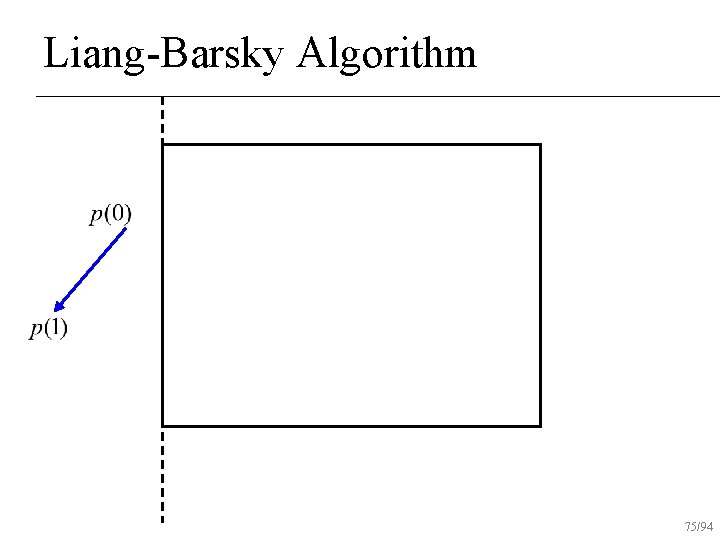
Liang-Barsky Algorithm Uses parametric form of line for clipping n Lines are oriented Classify lines as moving inside to out or outside to in n Don’t find actual intersection points Find parameter values on line to draw n 53/94

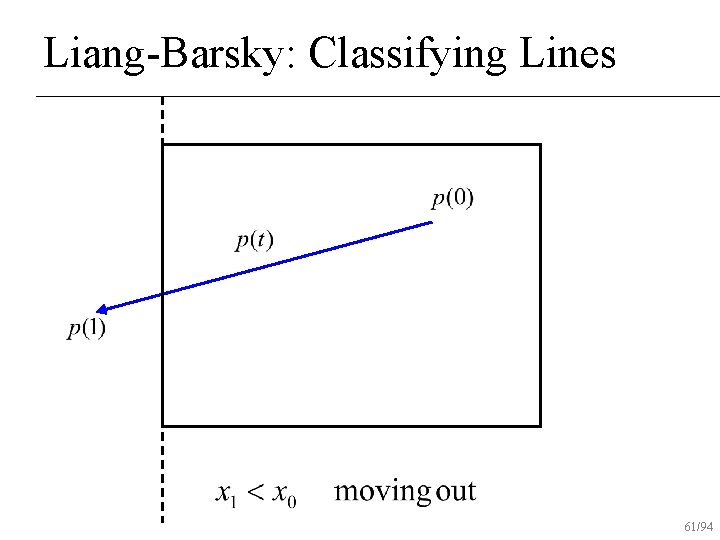
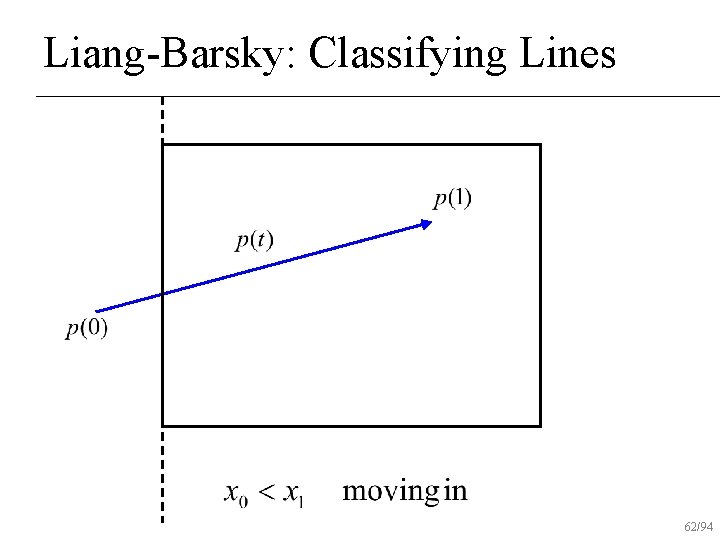
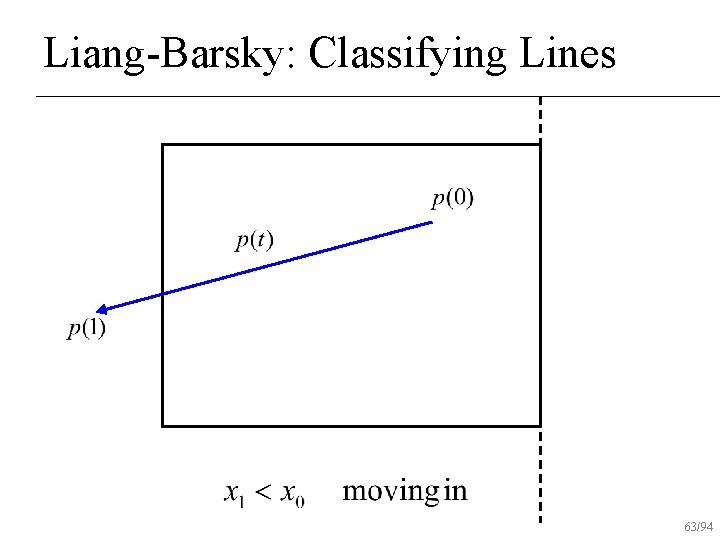
Liang-Barsky Algorithm Initialize interval to [tmin, tmax]=[0, 1] n For each boundary u Find parametric intersection t with boundary u If moving in to out, tmax = min(tmax, t) u else tmin = max(tmin, t) u If tmin>tmax, reject line n 54/94

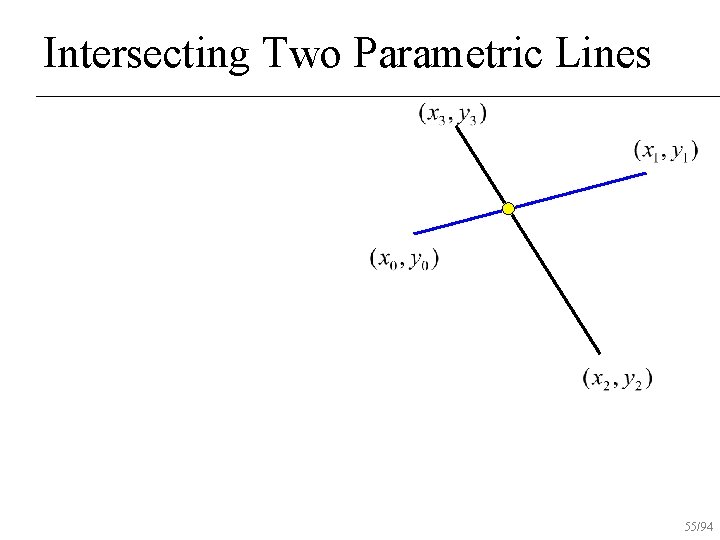
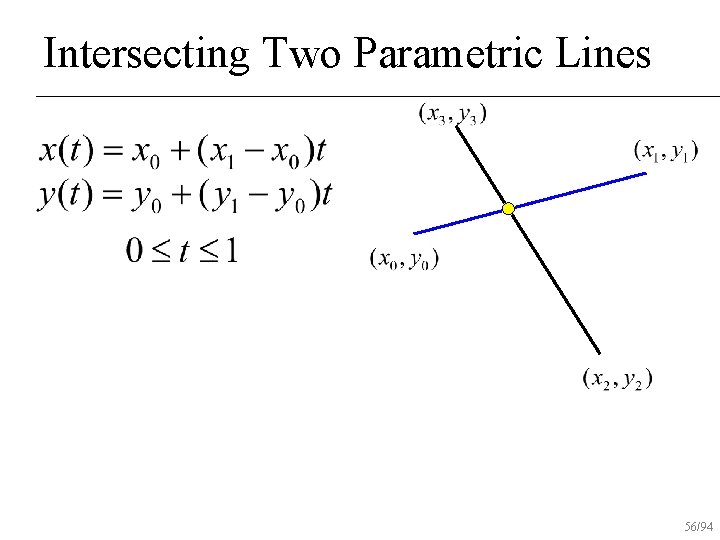
Intersecting Two Parametric Lines 55/94

Intersecting Two Parametric Lines 56/94

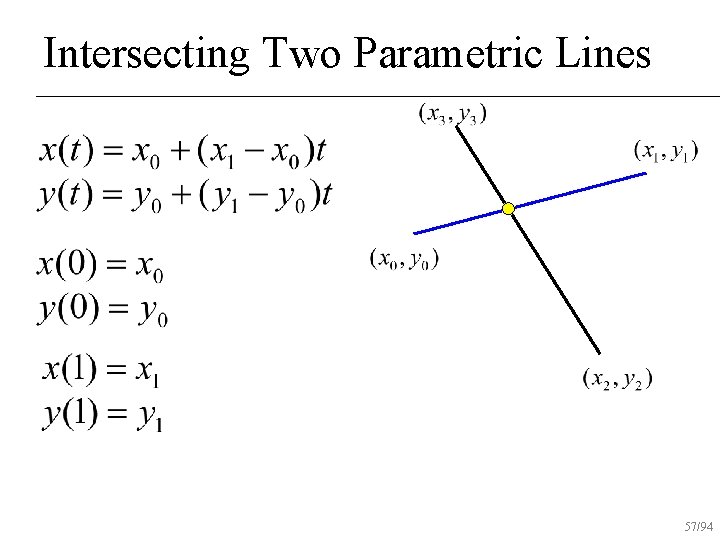
Intersecting Two Parametric Lines 57/94

Intersecting Two Parametric Lines 58/94

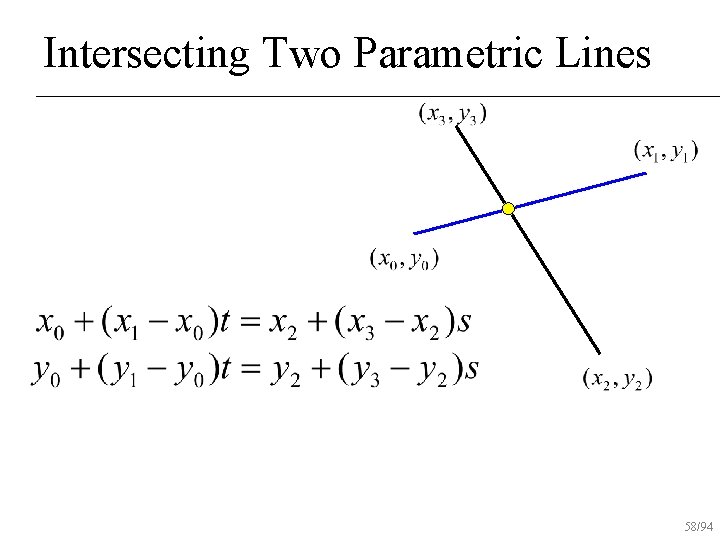
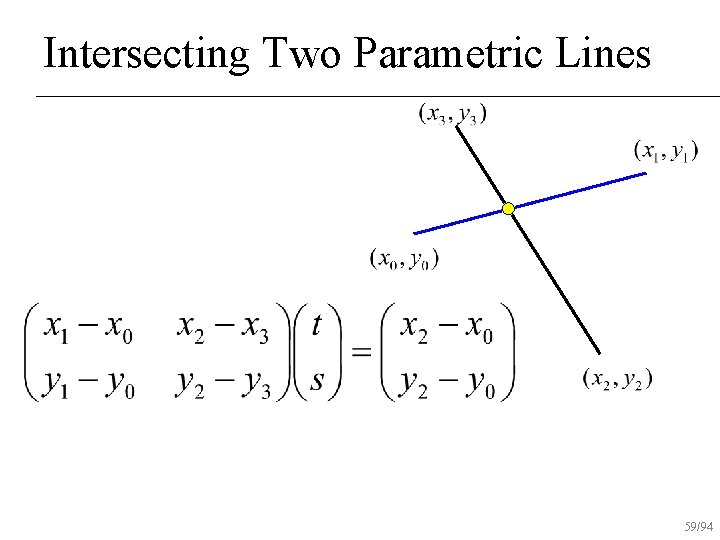
Intersecting Two Parametric Lines 59/94

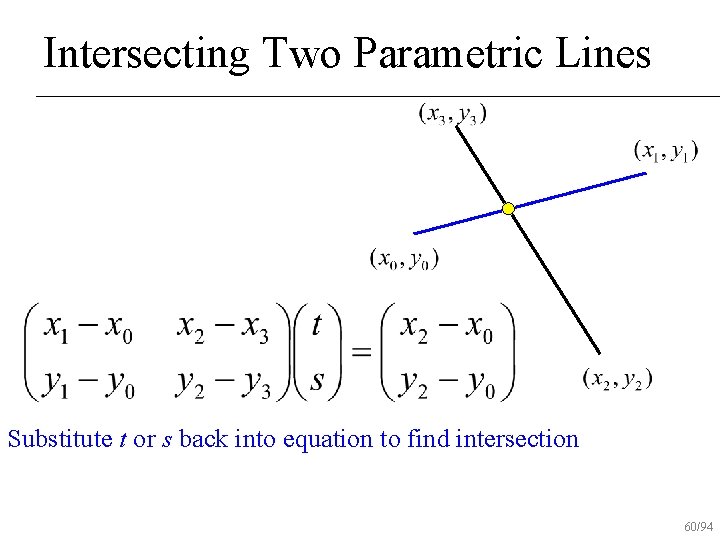
Intersecting Two Parametric Lines Substitute t or s back into equation to find intersection 60/94

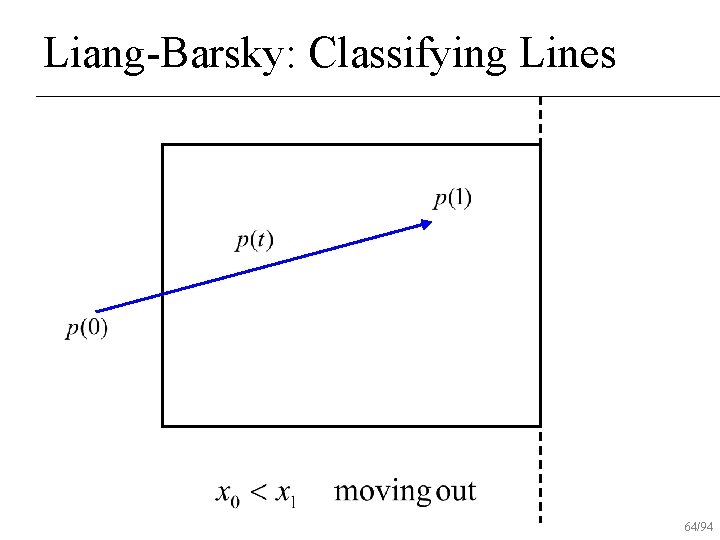
Liang-Barsky: Classifying Lines 61/94

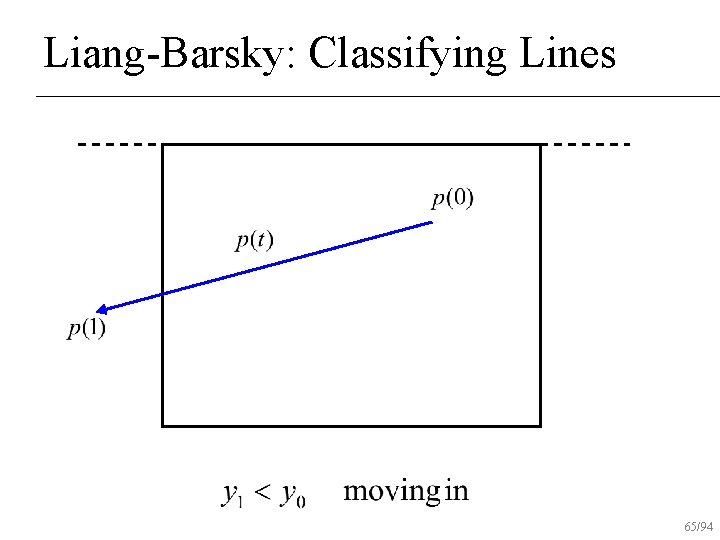
Liang-Barsky: Classifying Lines 62/94

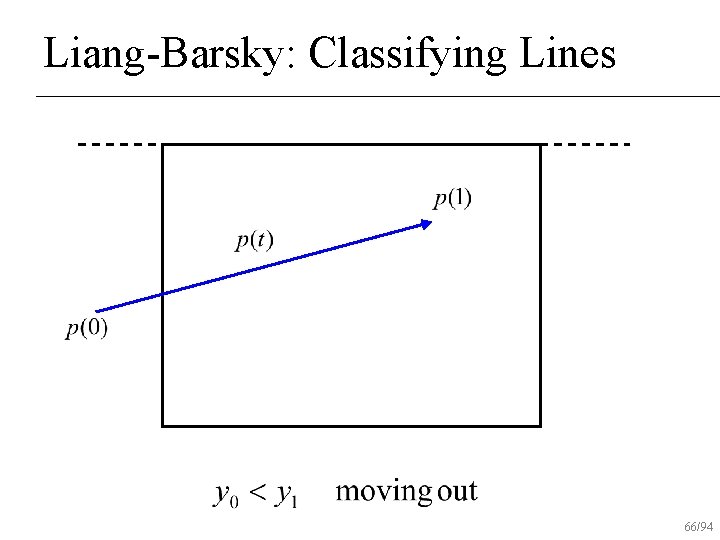
Liang-Barsky: Classifying Lines 63/94

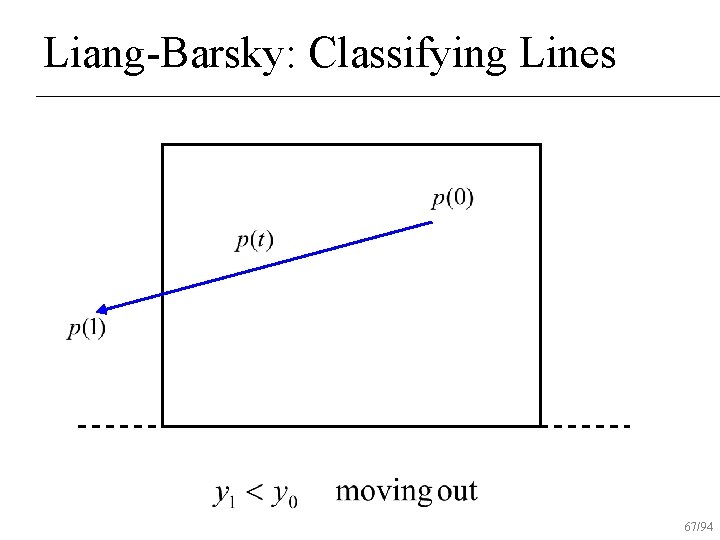
Liang-Barsky: Classifying Lines 64/94

Liang-Barsky: Classifying Lines 65/94

Liang-Barsky: Classifying Lines 66/94

Liang-Barsky: Classifying Lines 67/94

Liang-Barsky: Classifying Lines 68/94

Liang-Barsky Algorithm 69/94

Liang-Barsky Algorithm 70/94

Liang-Barsky Algorithm 71/94

Liang-Barsky Algorithm 72/94

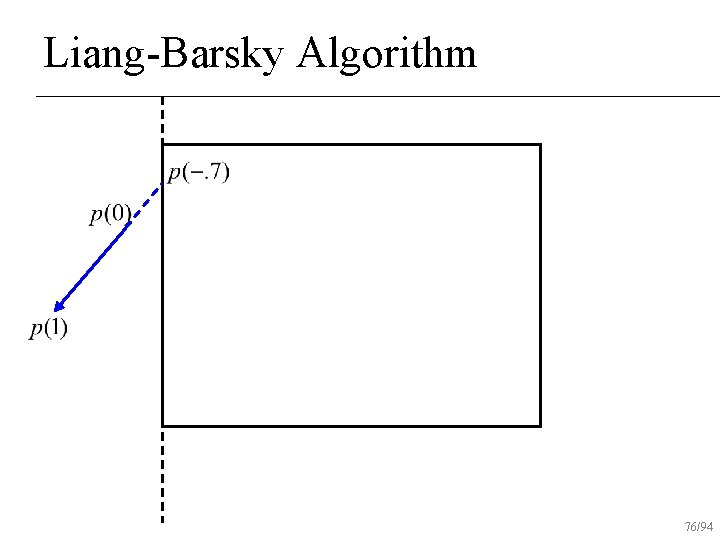
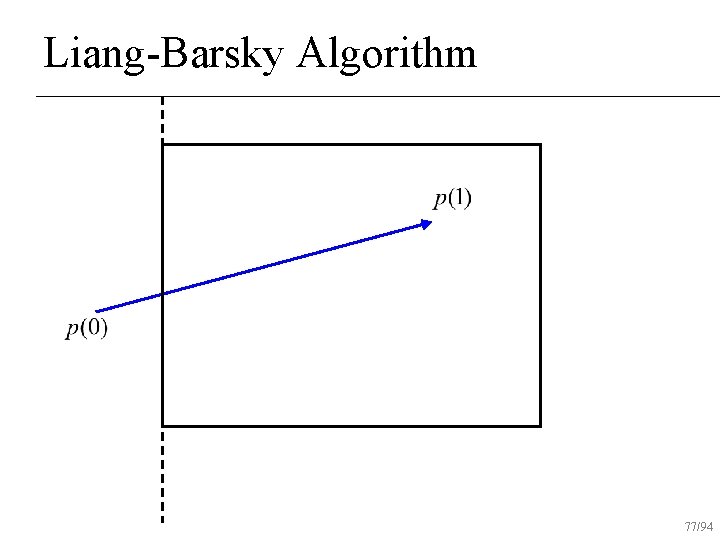
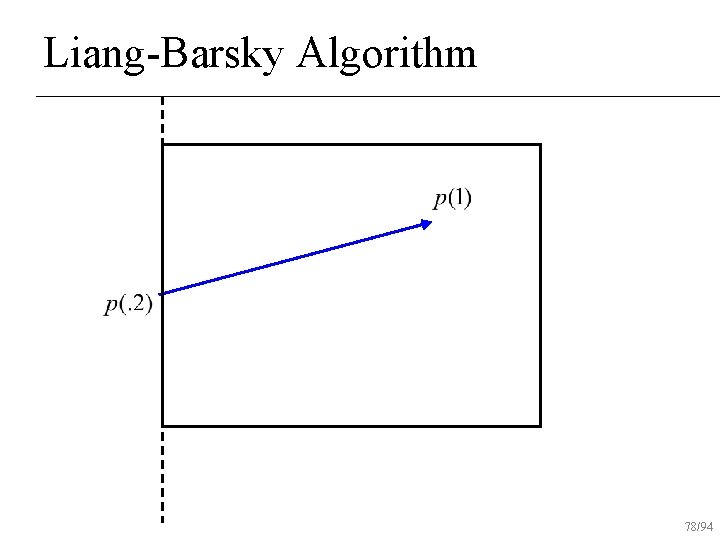
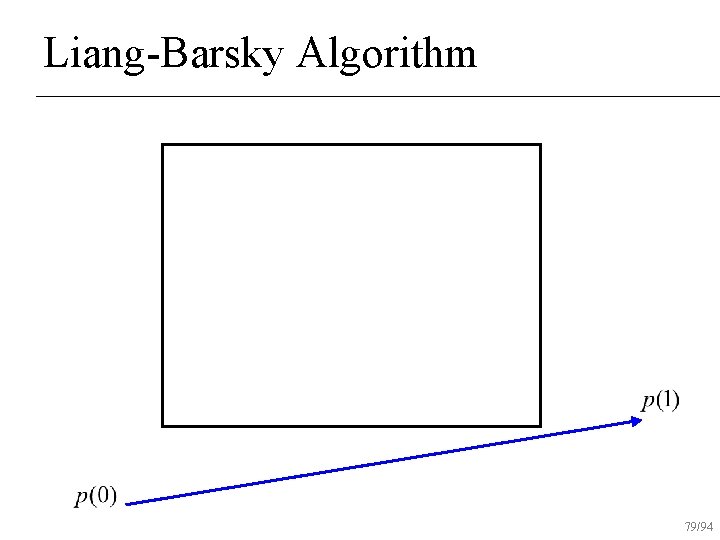
Liang-Barsky Algorithm 73/94

Liang-Barsky Algorithm 74/94

Liang-Barsky Algorithm 75/94

Liang-Barsky Algorithm 76/94

Liang-Barsky Algorithm 77/94

Liang-Barsky Algorithm 78/94

Liang-Barsky Algorithm 79/94

Liang-Barsky Algorithm 80/94

Liang-Barsky Algorithm 81/94

Liang-Barsky Algorithm 82/94

Liang-Barsky Algorithm 83/94

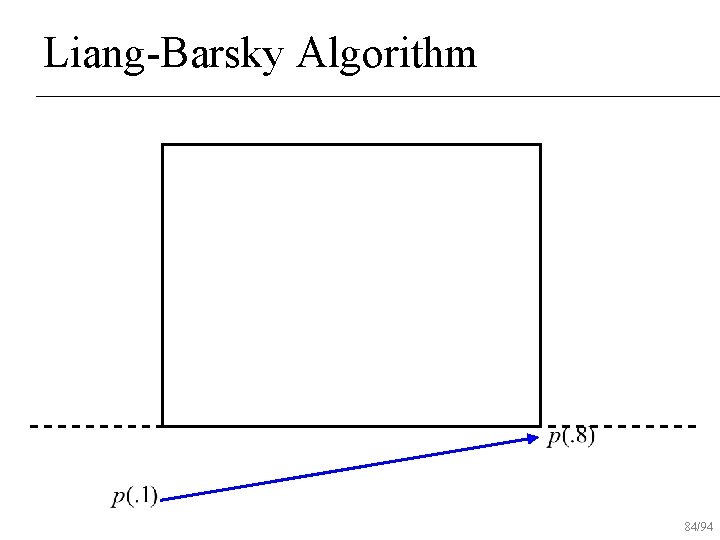
Liang-Barsky Algorithm 84/94

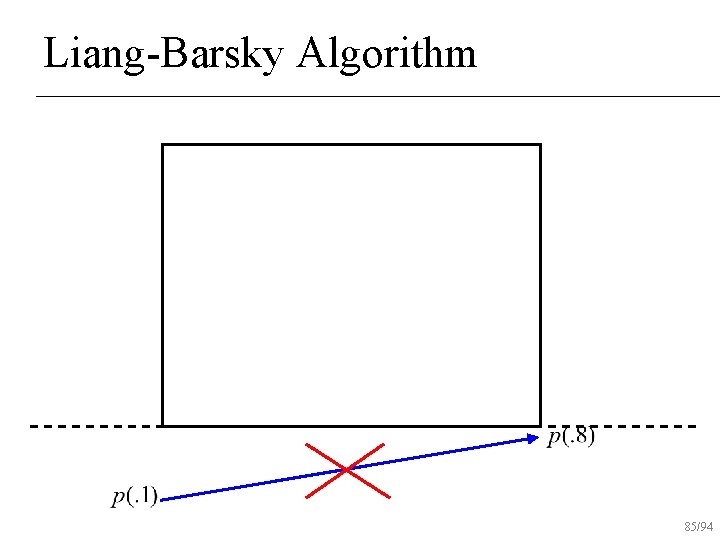
Liang-Barsky Algorithm 85/94

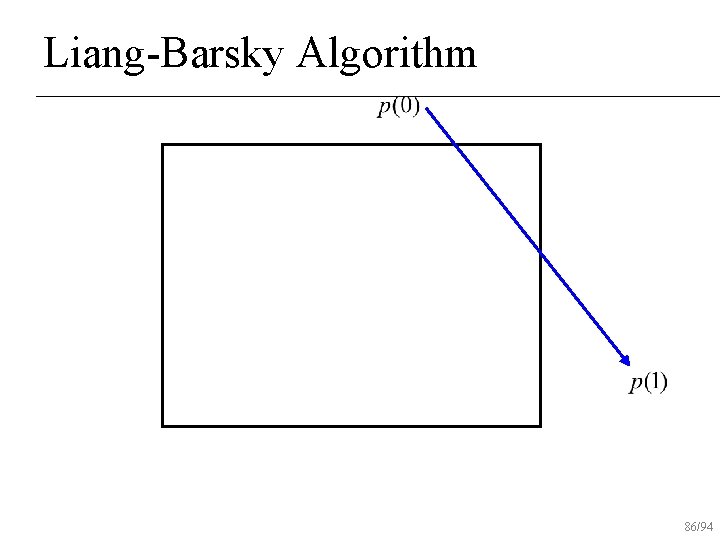
Liang-Barsky Algorithm 86/94

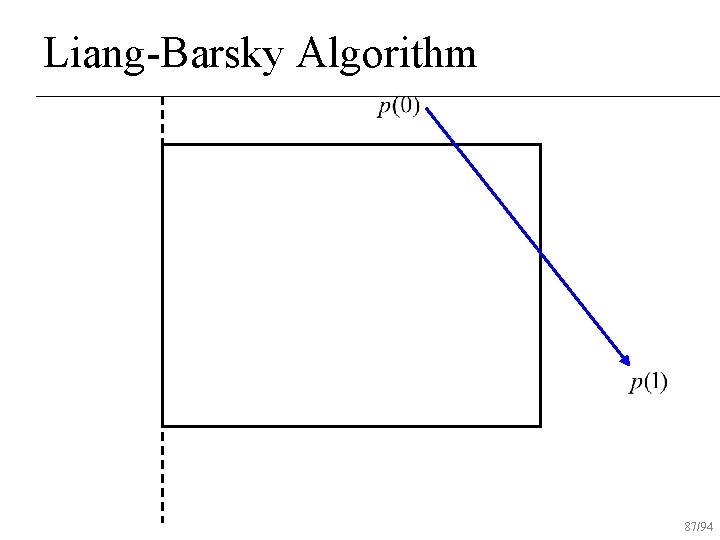
Liang-Barsky Algorithm 87/94

Liang-Barsky Algorithm 88/94

Liang-Barsky Algorithm 89/94

Liang-Barsky Algorithm 90/94

Liang-Barsky Algorithm 91/94

Liang-Barsky Algorithm 92/94

Comparison n Cohen-Sutherland Repeated clipping is expensive u Best used when trivial acceptance and rejection is possible for most lines u n Liang-Barsky Computation of t-intersections is cheap (only one division) u Computation of (x, y) clip points is only done once u Algorithm doesn’t consider trivial accepts/rejects u Best when many lines must be clipped u 93/94

Line Clipping – Considerations Just clipping end-points does not produce the correct results inside the window n Must also update sum in midpoint algorithm n n Clipping against non-rectangular polygons is also possible but seldom used 94/94