AMS 345CSE 355 Computational Geometry Lecture Polygons Guarding

AMS 345/CSE 355 Computational Geometry Lecture: Polygons, Guarding Joe Mitchell

Do You Like Puzzles? n n n Come to the new Stony Brook Puzzle Society Meets: Friday 1: 05 - 2: 30 pm at CSE 2120 Organizer: Pramod Ganapathi pganapathi@cs. stonybrook. edu

Simple Polygons n Definition: A simple polygon P is the (closed) region bounded by a “simple closed polygonal curve”.

Simple Polygon n Definition in [O’Rourke]:

Simple Polygons n Alternate Definition: P is a simple polygon if it is a simply connected (i. e. , no “holes”) subset of the plane whose boundary consists of a connected finite union of straight line segments.

Simple Polygons Some definitions would allow this as a “degenerate” simple polygon

Definitions: Visibility, Diagonals n For p, q in P, p is visible to q if segment pq lies within (closed) P p q

Definitions: Visibility, Diagonals n n For p, q in P, p is visible to q if segment pq lies within (closed) P p is clearly visible to q if p is visible to q AND the only points in common between pq and P are possibly p and q p clearly sees q but does not clearly see q’ p sees q’ p q q’

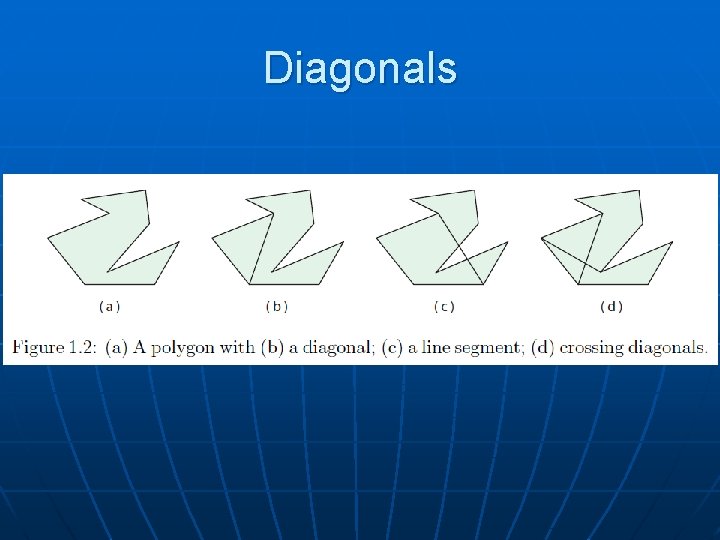
Definitions: Visibility, Diagonals n vivj is a diagonal if vi and vj are vertices that clearly see each other (versus: chord pq, with p and q on the boundary of P) q pq is a chord (not a diagonal) vivj is a diagonal vkvm is not a diagonal p vm vj vk vi

Diagonals

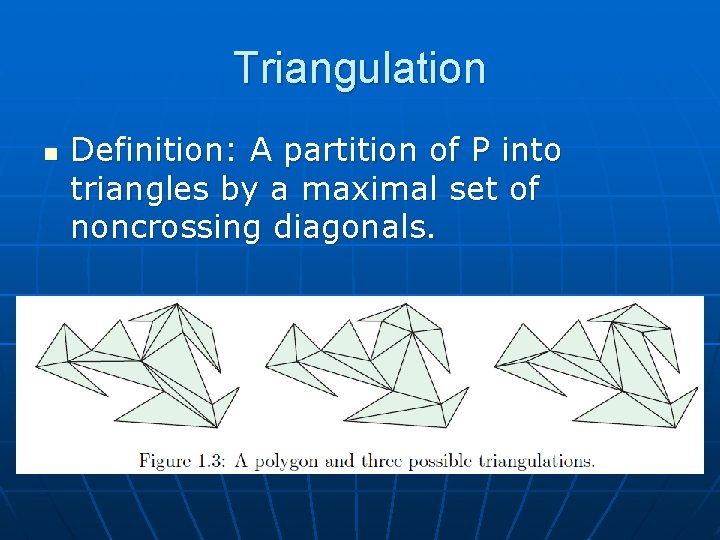
Triangulation n Definition: A partition of P into triangles by a maximal set of noncrossing diagonals.

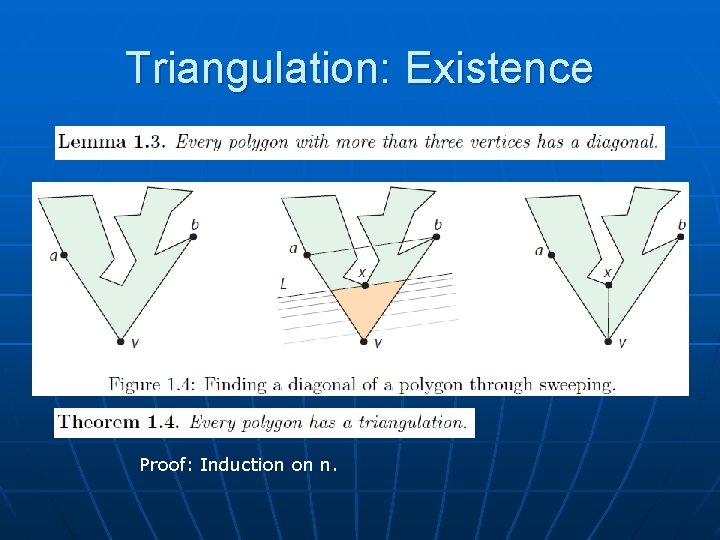
Triangulation: Existence Proof: Induction on n.

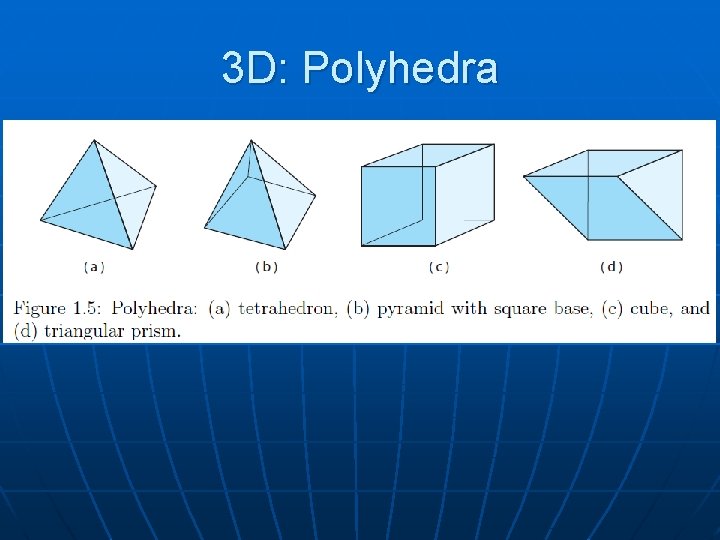
3 D: Polyhedra

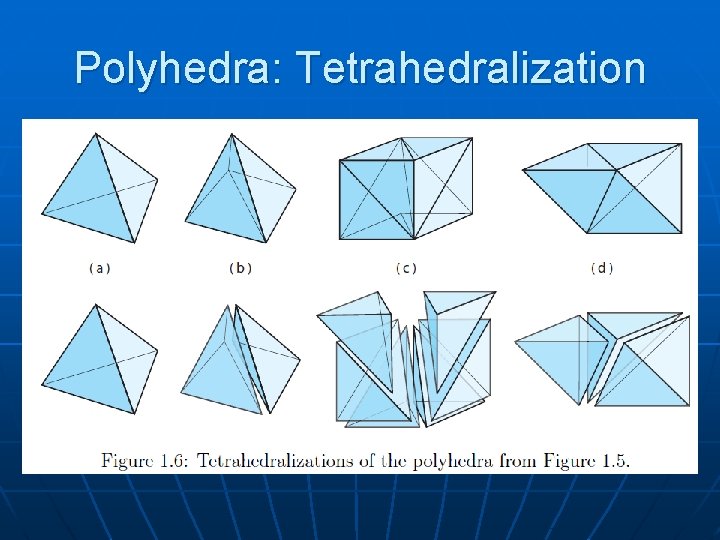
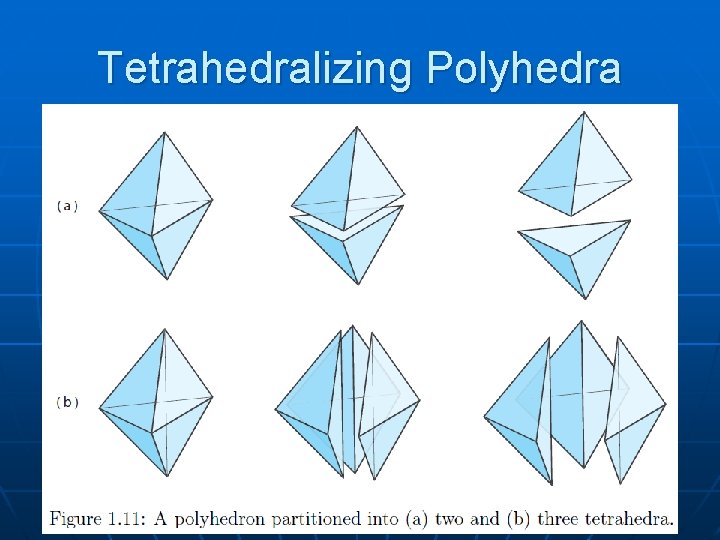
Polyhedra: Tetrahedralization

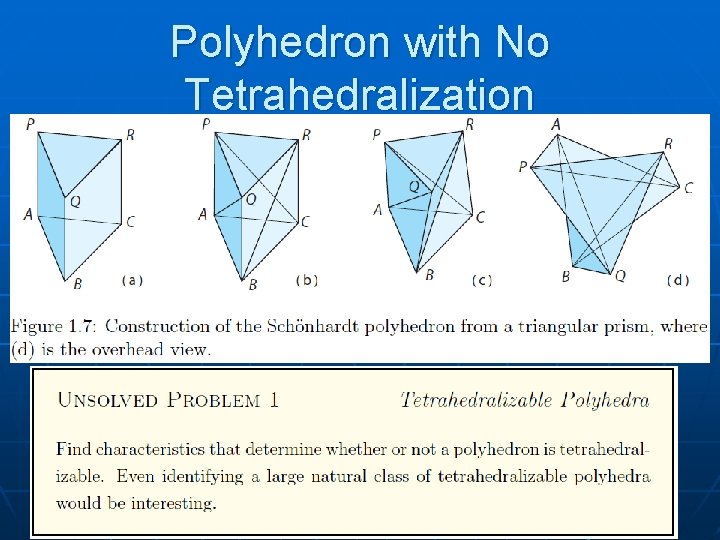
Polyhedron with No Tetrahedralization

Combinatorics: Triangulations Proof: induction on n. True for n=3 (trivially). Assume true for n=k (the Induction Hypothesis). Take an n-gon, P, with n=k+1. We know it has a diagonal (since n>3). The diagonal partitions P into two polygons, of sizes n 1 and n 2 , with n 1 +n 2 =n+2 (since the endpoints of the diagonal are counted twice) By IH, the two subpolygons have triangulation with n 1 -2 and n 2 -2 triangles; glue together along the diagonal to get a total of (n 1 -2)+(n 2 -2)=n-2 triangles in the overall triangulation. Similar for number of diagonals.

Ears n n A diagonal of the form vi-1 vi+1 is an ear diagonal; the triangle vi-1 vivi+1 is an ear, and vi is the ear tip Note that there at most n ears (and that a convex polygon has exactly n ears) vi+1 vi-1 vi

Ears Proof(1): There are n edges of P and n-2 triangles in any triangulation. Imagine dropping the n edges into the n-2 “pigeonholes” corresponding to the triangles: Each edge appears on boundary of some triangle. By pigeonhole principle, at least 2 triangles get 2 edges “dropped in their box”. (2) Consider the planar dual (excluding the face at infinity) of a triangulation of P. Claim: The dual graph for a triangulated simple polygon is a TREE. Any tree of 2 or more nodes has at least 2 nodes of degree 1.

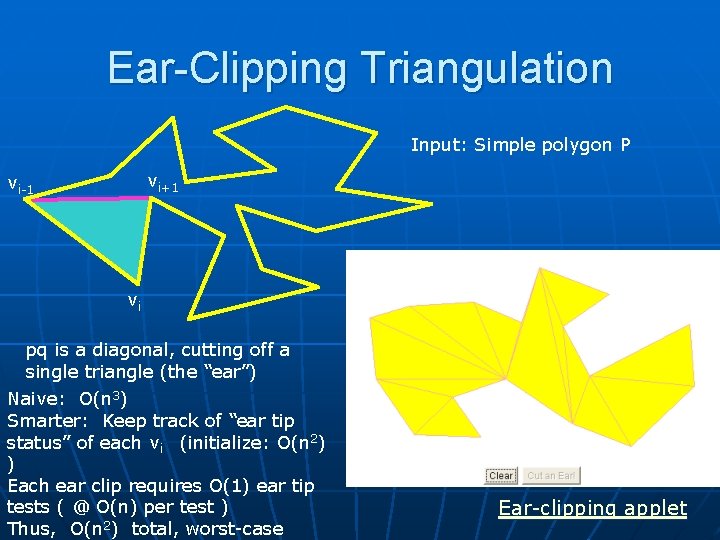
Ear-Clipping Triangulation Input: Simple polygon P vi+1 vi-1 vi pq is a diagonal, cutting off a single triangle (the “ear”) Naive: O(n 3) Smarter: Keep track of “ear tip status” of each vi (initialize: O(n 2) ) Each ear clip requires O(1) ear tip tests ( @ O(n) per test ) Thus, O(n 2) total, worst-case Ear-clipping applet

Number of Triangulations The diagonals, together with the edges of convex polygon P, form the complete graph, Kn

Number of Triangulations: Convex Polygons The first Catalan numbers, for n=1, 2, 3, … are given by: 1, 2, 5, 14, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, …

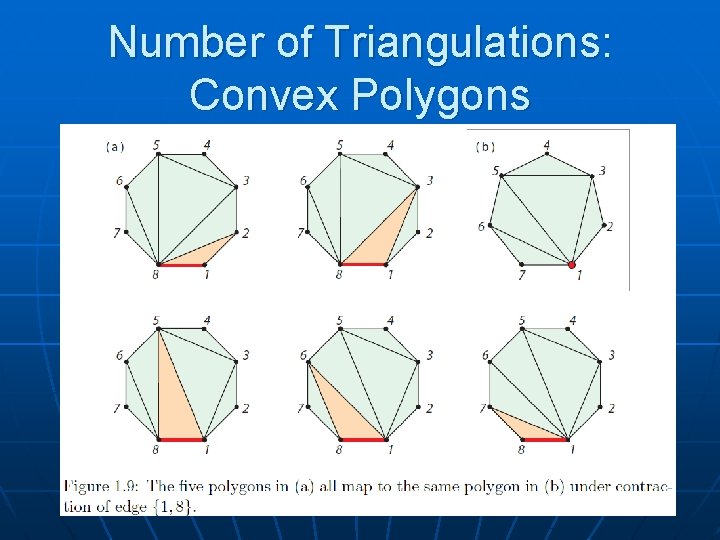
Number of Triangulations: Convex Polygons

Number of Triangulations: Convex Polygons

Number of Triangulations: Simple Polygons Question: Is it possible to find a simple polygon P having exactly k triangulations, for every positive integer k?

Exercise n Can you find a simple polygon that has exactly 3 different triangulations?

Number of Triangulations: Simple Polygons

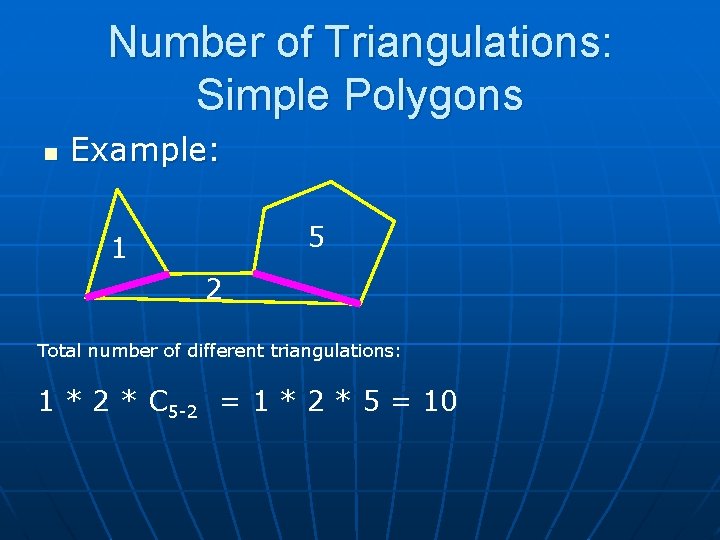
Number of Triangulations: Simple Polygons n Example: Diagonals Set of all diagonals, together with the edges of P, forms the visibility graph of P Forced diagonals: Must be in ANY triangulation of P: Any diagonal that is not crossed by other diagonals.

Number of Triangulations: Simple Polygons n Example: 5 1 2 Total number of different triangulations: 1 * 2 * C 5 -2 = 1 * 2 * 5 = 10

More Examples: HW 1

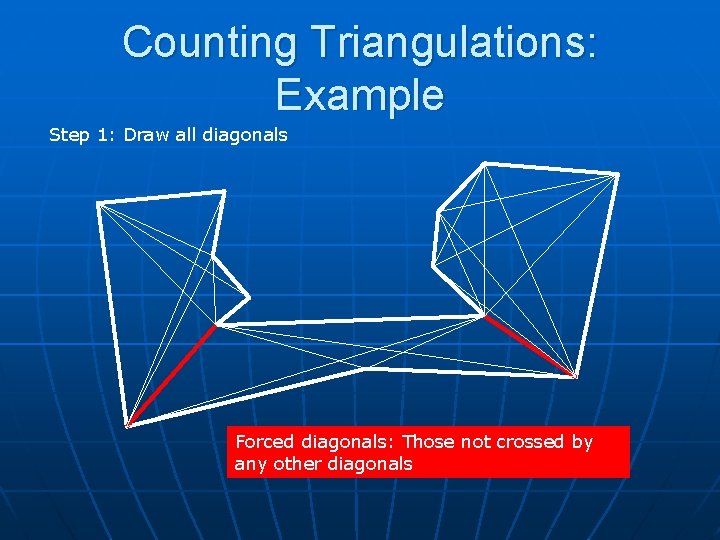
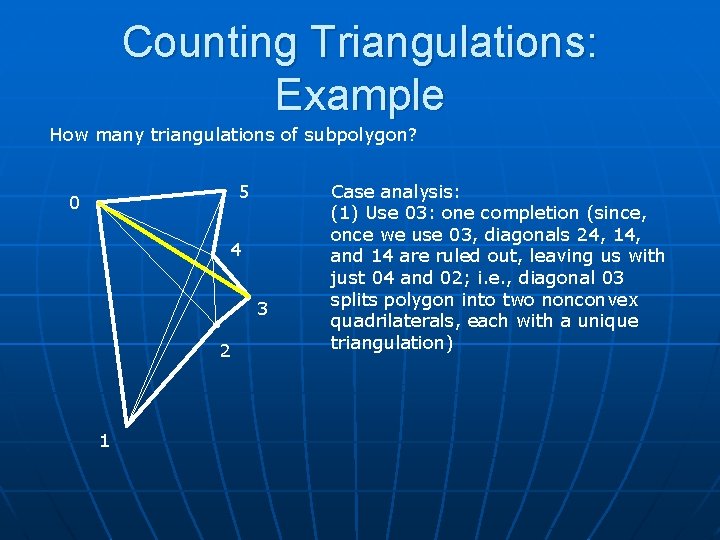
Counting Triangulations: Example

Counting Triangulations: Example Step 1: Draw all diagonals Forced diagonals: Those not crossed by any other diagonals

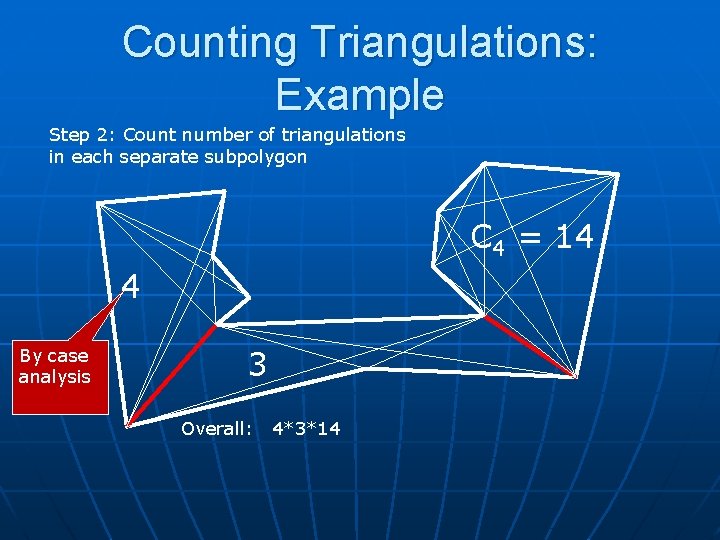
Counting Triangulations: Example Step 2: Count number of triangulations in each separate subpolygon C 4 = 14 4 By case analysis 3 Overall: 4*3*14

Counting Triangulations: Example How many triangulations of subpolygon? 5 0 4 3 2 1 Case analysis: (1) Use 03: one completion (since, once we use 03, diagonals 24, 14, and 14 are ruled out, leaving us with just 04 and 02; i. e. , diagonal 03 splits polygon into two nonconvex quadrilaterals, each with a unique triangulation)

Counting Triangulations: Example How many triangulations? 5 0 4 3 2 1 Case analysis: (1)Use 03: one completion (2) Do NOT Use 03: Then, 24 is forced, and there are 3 triangulations possible (using 15 and 14, or 04 and 02). Total for cases (1) and (2): 1+3=4

Counting Triangulations n n n Efficient algorithm? Yes! (for simple polygons P, but not for polygons with holes) Idea: use “dynamic programming” (recursive solution)

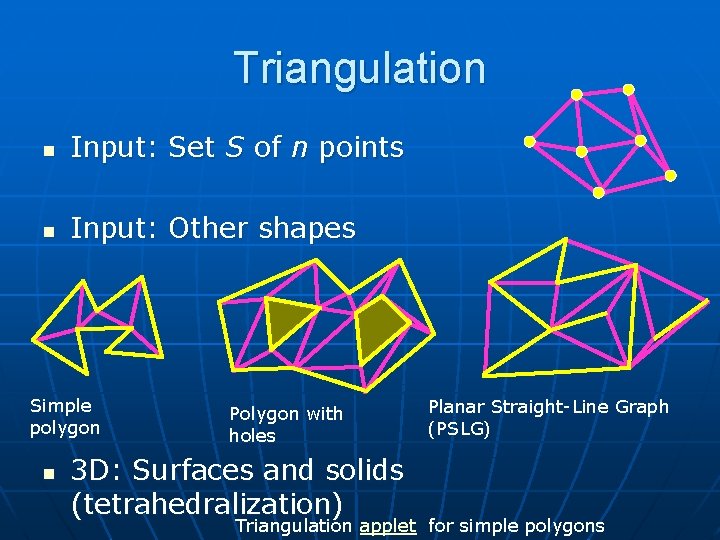
Triangulation n Input: Set S of n points n Input: Other shapes Simple polygon n Polygon with holes 3 D: Surfaces and solids (tetrahedralization) Planar Straight-Line Graph (PSLG) Triangulation applet for simple polygons

Triangulation Theory in 2 D n Also with holes Thm: A simple polygon has a triangulation. • Lem: An n-gon with n 4 has a diagonal. But, NOT true in 3 D! n n Thm: Any triangulation of a simple n-gon has n-3 diagonals, n-2 triangles. Thm: The “dual” graph is a tree. Thm: An n-gon with n 4 has 2 “ears”. Thm: The triangulation graph can be 3 -colored. Proofs: Induction on n.

Triangulating a Polygon n n Simple “ear-clipping” methods: O(n 2 ) Cases with simple O(n) algorithms: • Convex polygons (trivial!) fan • Monotone polygons, monotone mountains n General case (even with holes!): • Sweep algorithm to decompose into monotone mountains • O(n log n) n Best theoretical results: Not practical! • Simple polygons: O(n) [Chazelle’ 90] • Polygons with h holes: O(n+h log 1+ h), (n+h log h) [BC] n Good practical method: FIST [Held], based on clever methods of ear clipping (worst-case O(n 2 ) )

Tetrahedralizing Polyhedra

Tetrahedralizing Polyhedra

Today, 9/5/13 n n n Review triangulation Guarding problem Art Gallery Theorem Computing guard numbers by hand Examples Begin Convex Hulls

Guarding Polygons V(p) = visibility polygon of p inside P = set of all points q that p sees in P

Guarding Polygons Goal: Find a set of points (“guards”) within P so that their VP(p) sets cover P “Guard cover” “Point guards” versus “vertex guards” Regular visibility versus “clear visibility”

Min-Guard Coverage Problem Determine a small set of guards to see all of a given polygon P 5 guards suffice to cover P (what about 4 guards? 3? ) Computing min # of guards, g(P), for n-gon P is NP-hard Challenge/open: Compute g(P) approximately

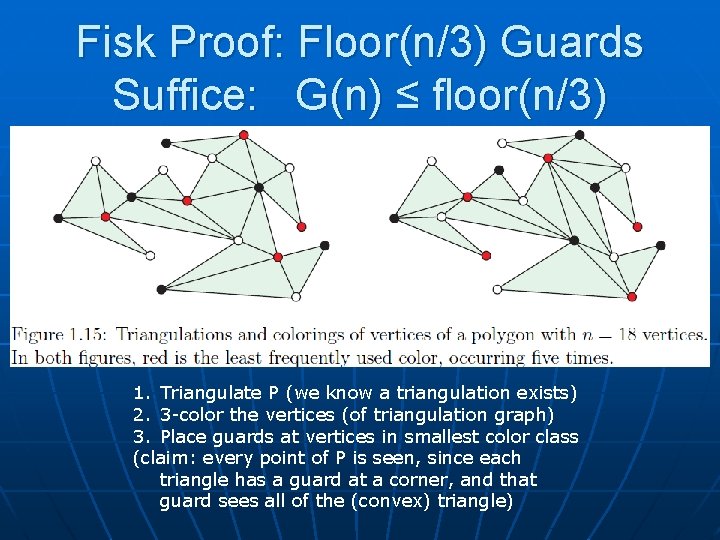
Art Gallery Theorem The Combinatorics of Guarding n n Answers a question of Victor Klee: How many guards are needed to see a simple n-gon? Proofs: Chvatal (induction); Fisk (simple coloring argument) g(P) = min number of guards for P G(n) = max of g(P), over all n-gons P What is G(n)? Answer: G(n) = floor(n/3) In fact, floor(n/3) vertex guards suffice

Chvatal Comb: Necessity of n/3 Guards in Some Cases w 1 w 2 Shows that some n-gons require at least n/3 guards, since we can place “independent witness points”, wi , near each tip, and must have a separate guard in each of their visibility regions (triangles) Can extend to cases where n is not a multiple of 3, showing lower bound of floor(n/3). Thus: G(n) ≥ floor(n/3)

Fisk Proof: Floor(n/3) Guards Suffice: G(n) ≤ floor(n/3) 1. Triangulate P (we know a triangulation exists) 2. 3 -color the vertices (of triangulation graph) 3. Place guards at vertices in smallest color class (claim: every point of P is seen, since each triangle has a guard at a corner, and that guard sees all of the (convex) triangle)

Vertex Guarding a Simple Polygon n Vertex guarding applet 11 yellow vertices 11 blue vertices 16 white vertices Place guards at yellow (or blue) vertices: at most n/3 vertex guards (here, n=38)

Computing g(P) by Inspection n n By inspection, find a large set of “visibility independent witness points” within P If we find w indep witness points, then we know that g(P)≥w By inspection, find a small set of m guards that see all of P: g(P)≤m If we are lucky, m=w; otherwise, more arguments are needed!

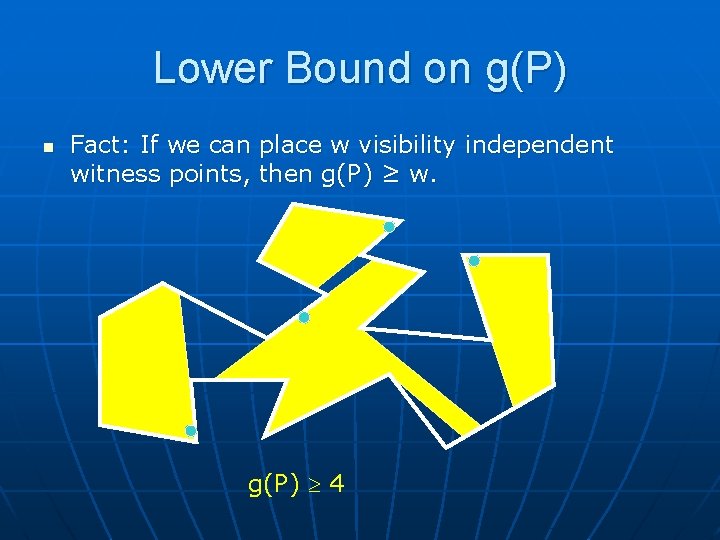
Lower Bound on g(P) n Fact: If we can place w visibility independent witness points, then g(P) ≥ w. g(P) 4

Witness Number n n n Let w(P) = max # of independent witness points possible in a set of visibility independent witness points for P Then, g(P) ≥ w(P) Note: It is hard to find g(P); it is poly -time to find w(P) Some polygons have g(P)=w(P); I call these perfect polygons – they are very special; most polygons P have a “gap”: g(P)>w(P)

Witness Number: Vertex Guards n n We say that a set, W, of points inside P are independent with respect to vertex guards if, for any two points of W, the set of vertices of P they see are disjoint Let w. V(P) = max # of witness points possible in a set of witness points for P that are indep wrt vertex guards Then, g. V(P) ≥ w. V(P) Note: It is hard to find g. V(P); a recent (unpublished) algorithm computes w. V(P) in polytime.

Useful Polygon Example n “Godfried’s Favorite Polygon” g(P)=2, but w(P)=1

Useful Polygon Examples n “Godfried’s Favorite Polygon” variations

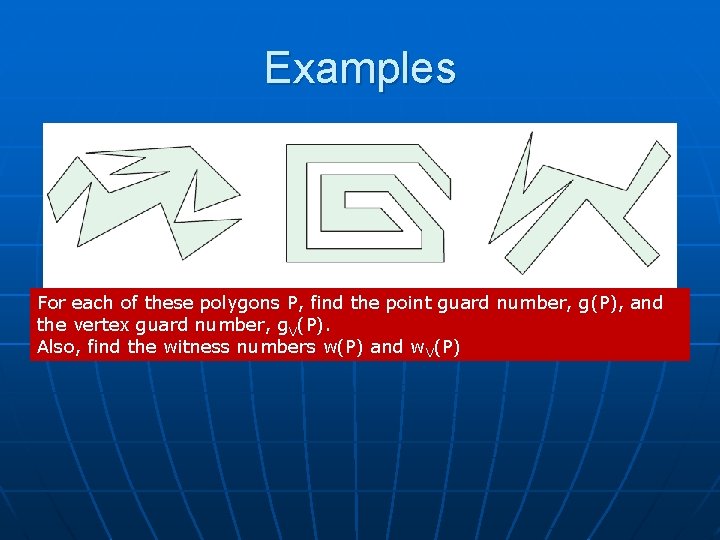
Examples For each of these polygons P, find the point guard number, g(P), and the vertex guard number, g. V(P). Also, find the witness numbers w(P) and w. V(P)

Visibility Graphs VG of P: (V, E), where E = set of all pairs of vertices of P that see each other, V = vertices (clear-VG: demand clear visibility: i. e. , edge set E is set of all diagonals) n

Art Gallery Theorem: Orthogonal (Rectilinear) Polygons

Polygons with Holes n n Art Galley Theorem: floor( (n+h)/3 ) guards suffice and are sometimes necessary (easy: floor( (n+2 h)/3 ) suffice – do you see why? )

Exterior Guarding: Fortress Problem

Edge Guards

Mirrored Galleries

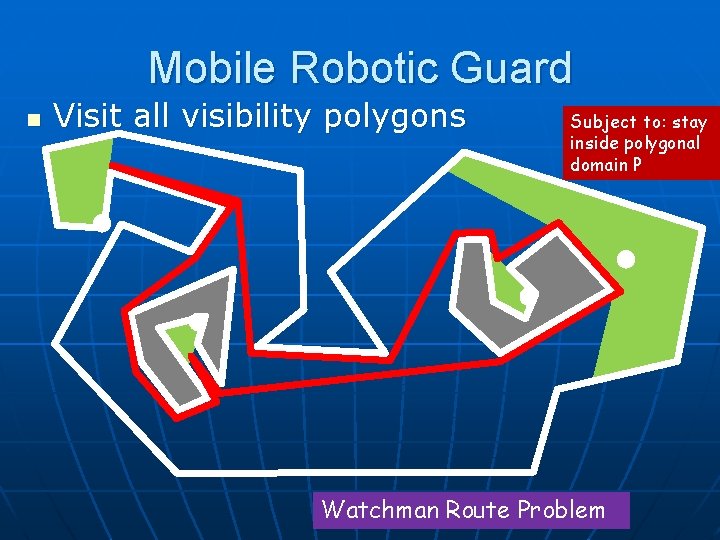
Mobile Guards n n n Find shortest route (path or tour) for a mobile guard within P: Watchman route problem Efficient algorithms for simple polygons P NP-hard for polygons with holes (as hard as the TSP)

Mobile Robotic Guard n Visit all visibility polygons Subject to: stay inside polygonal domain P Watchman Route Problem

Guarding Polyhedra n Note: Guards at vertices are NOT enough!

Scissors Congruence in 2 D n Dissections

Scissors Congruence in 2 D

Scissors Congruence in 2 D

Scissors Congruence in 2 D

Scissors Congruence: Rectangles

Scissors Congruence: Rectangles

Scissors Congruence: Polygons

Scissors Congruence: Polygons

Scissors Congruence: Polygons

Fair Partitions: Polygons

Scissors Congruence: 3 D

Scissors Congruence: 3 D