Chapter 3 Determinants 3 1 The Determinant of




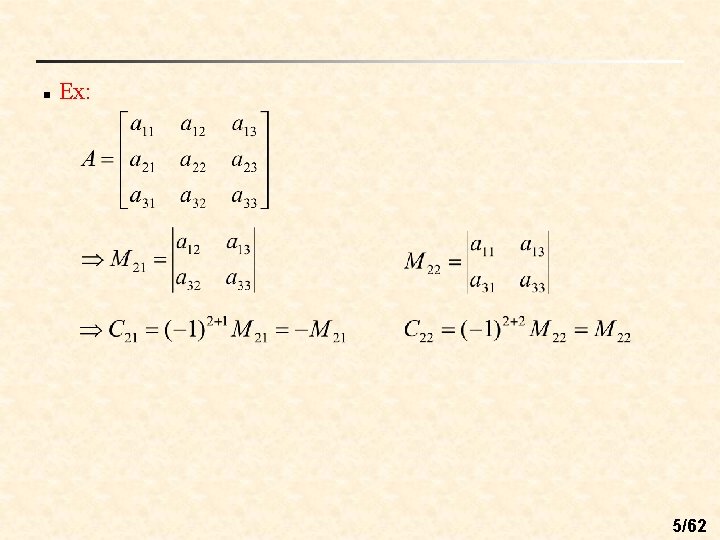







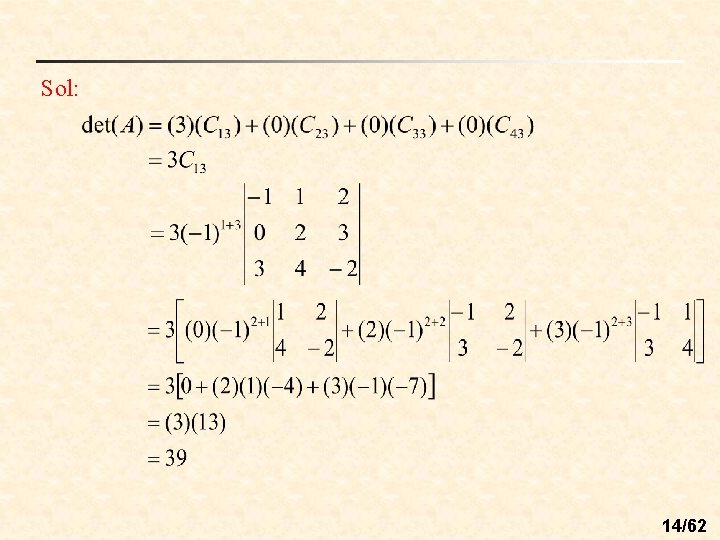

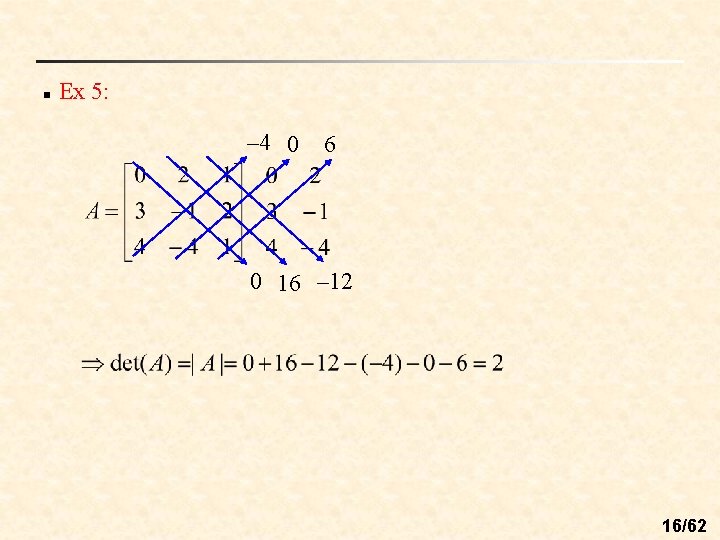





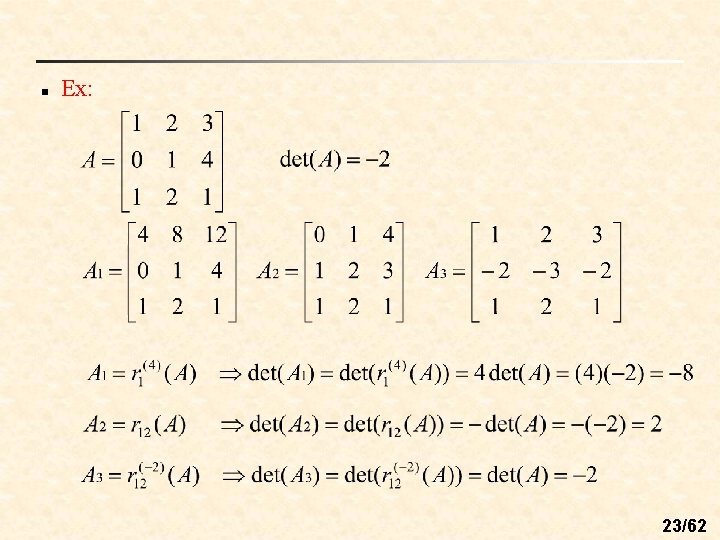


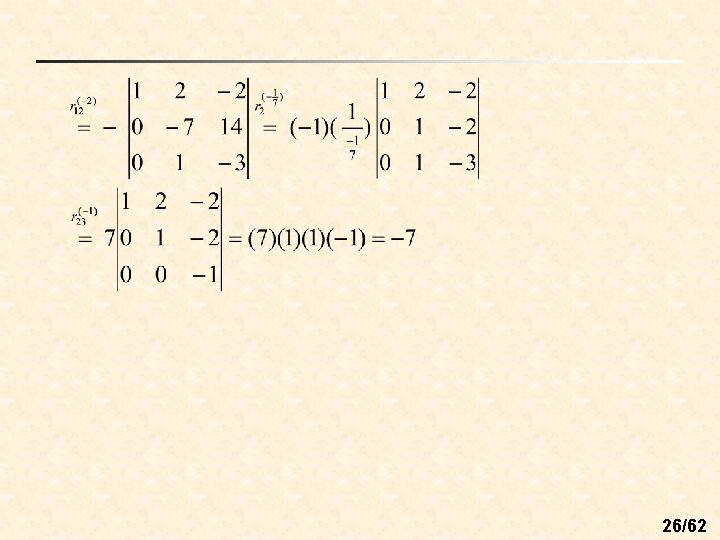
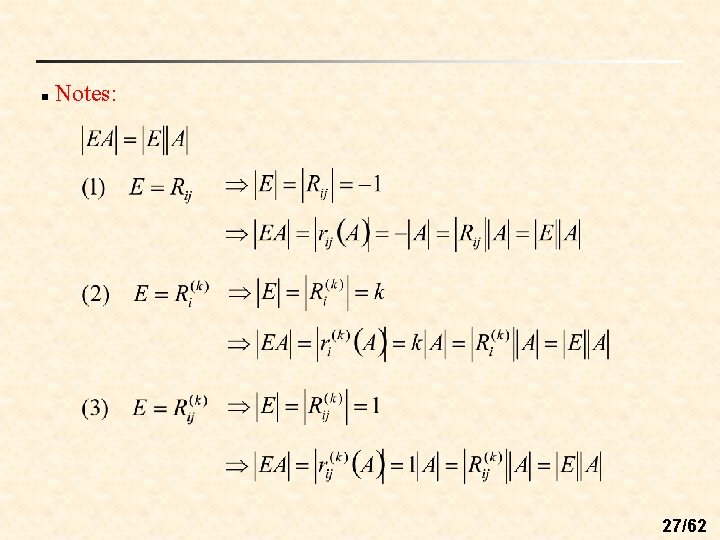

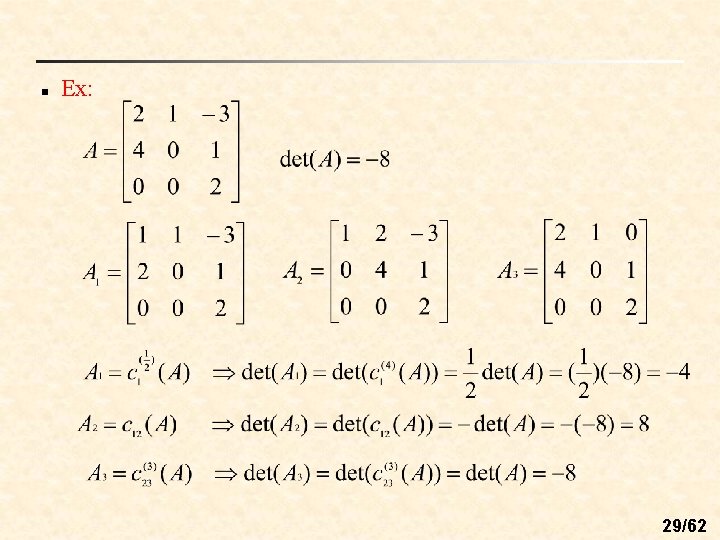

















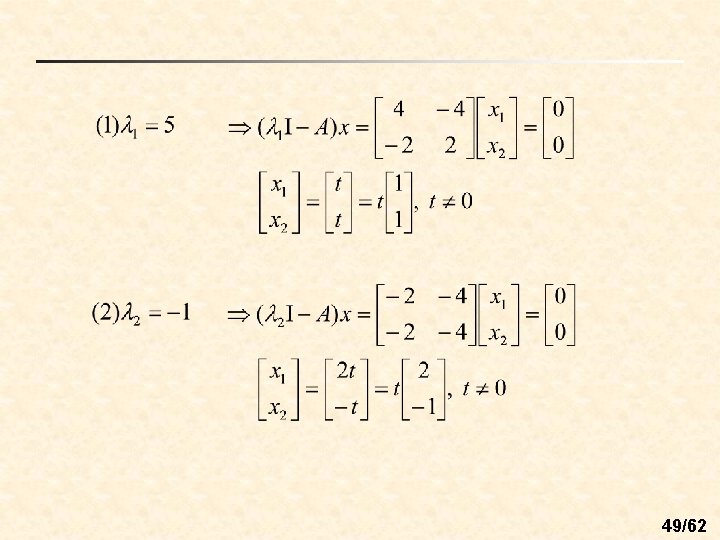






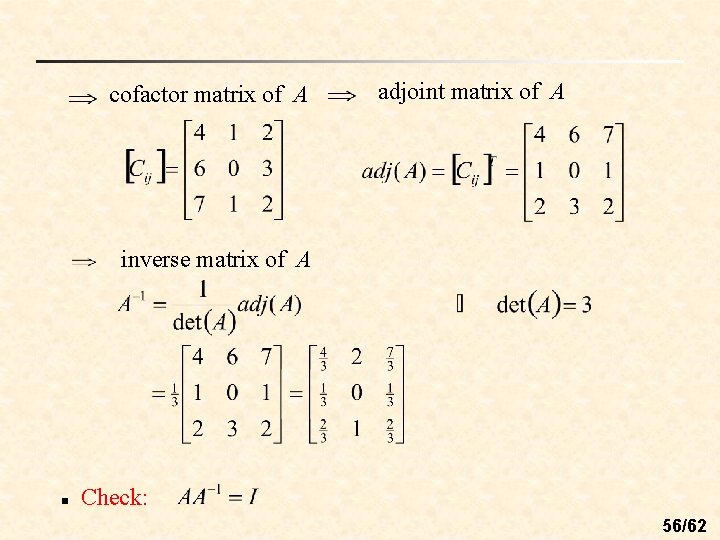

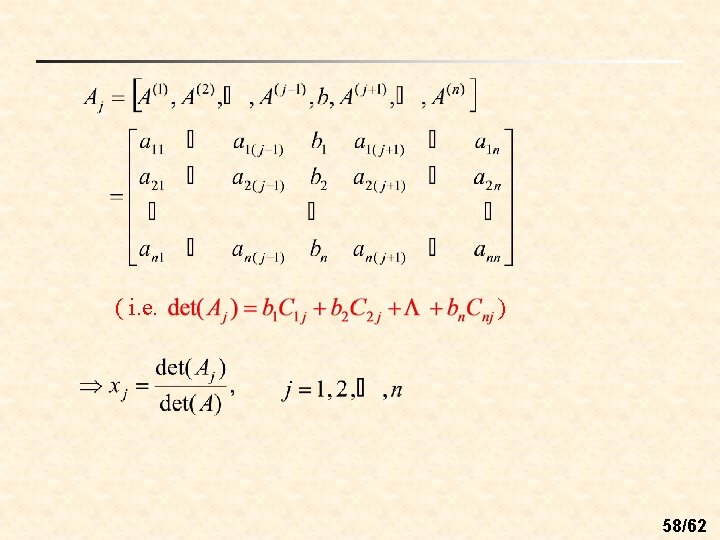
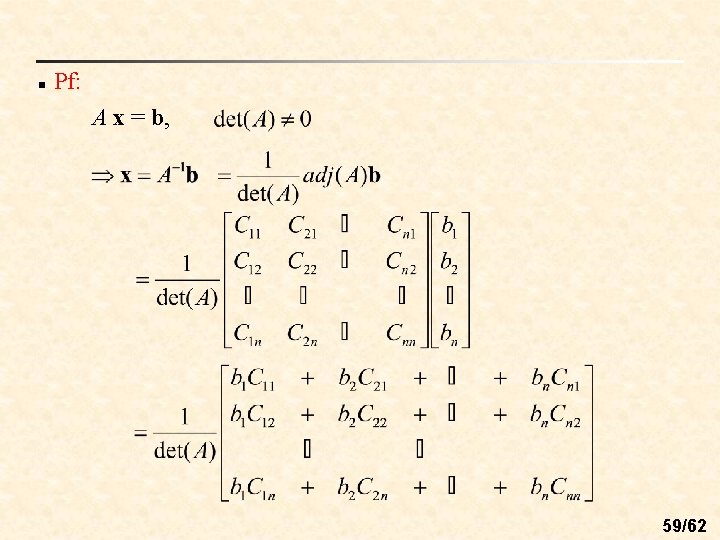
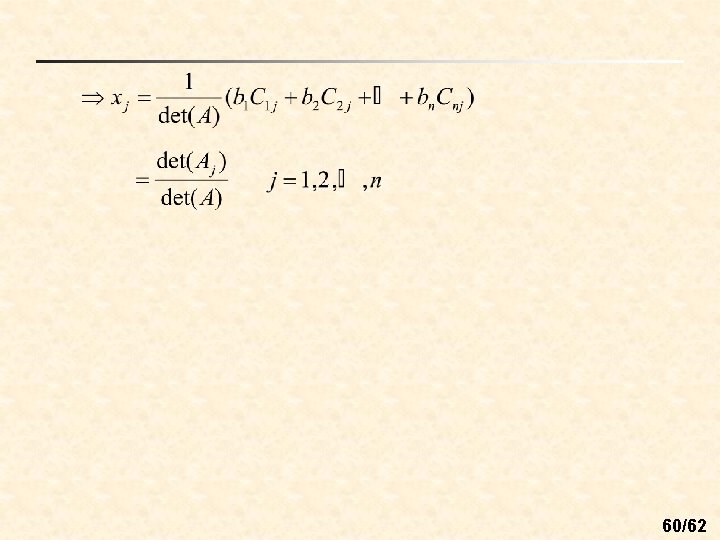


- Slides: 62

Chapter 3 Determinants 3. 1 The Determinant of a Matrix 3. 2 Evaluation of a Determinant using Elementary Operations 3. 3 Properties of Determinants 3. 4 Application of Determinants

3. 1 The Determinant of a Matrix n the determinant of a 2 × 2 matrix: n Note: 2/62

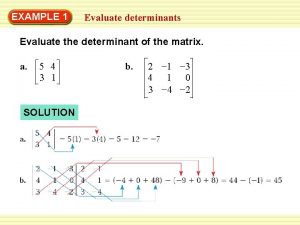
n Ex. 1: (The determinant of a matrix of order 2) n Note: The determinant of a matrix can be positive, zero, or negative. 3/62

n n Minor of the entry : The determinant of the matrix determined by deleting the ith row and jth column of A Cofactor of : 4/62
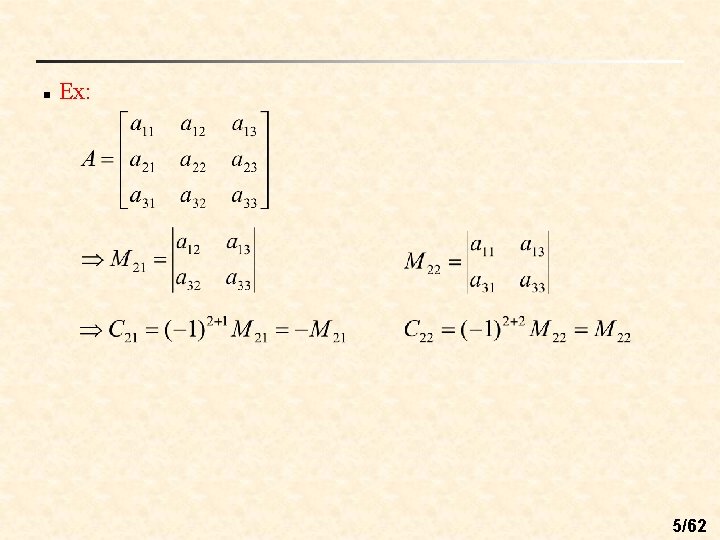
n Ex: 5/62

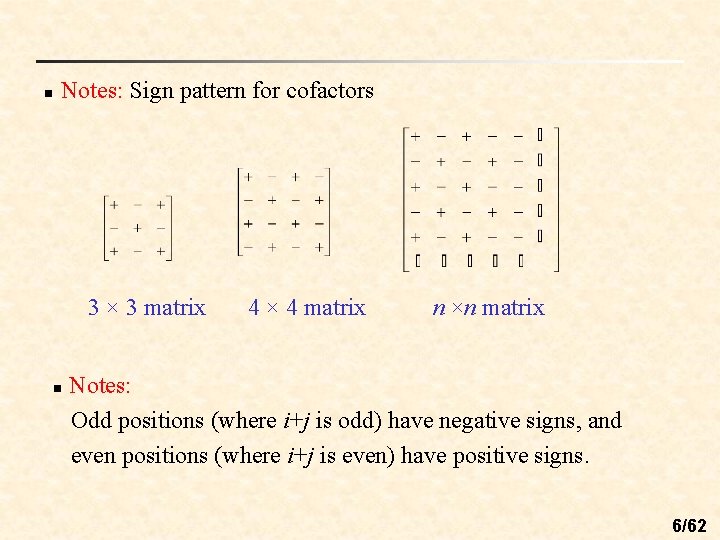
n Notes: Sign pattern for cofactors 3 × 3 matrix n 4 × 4 matrix n ×n matrix Notes: Odd positions (where i+j is odd) have negative signs, and even positions (where i+j is even) have positive signs. 6/62

n Ex 2: Find all the minors and cofactors of A. Sol: (1) All the minors of A. 7/62

Sol: (2) All the cofactors of A. 8/62

n Thm 3. 1: (Expansion by cofactors) Let A is a square matrix of order n. Then the determinant of A is given by (Cofactor expansion along the i-th row, i=1, 2, …, n ) or (Cofactor expansion along the j-th row, j=1, 2, …, n ) 9/62

n Ex: The determinant of a matrix of order 3 10/62

n Ex 3: The determinant of a matrix of order 3 Sol: 11/62

n Ex 5: (The determinant of a matrix of order 3) Sol: 12/62

n n Notes: The row (or column) containing the most zeros is the best choice for expansion by cofactors. Ex 4: (The determinant of a matrix of order 4) 13/62
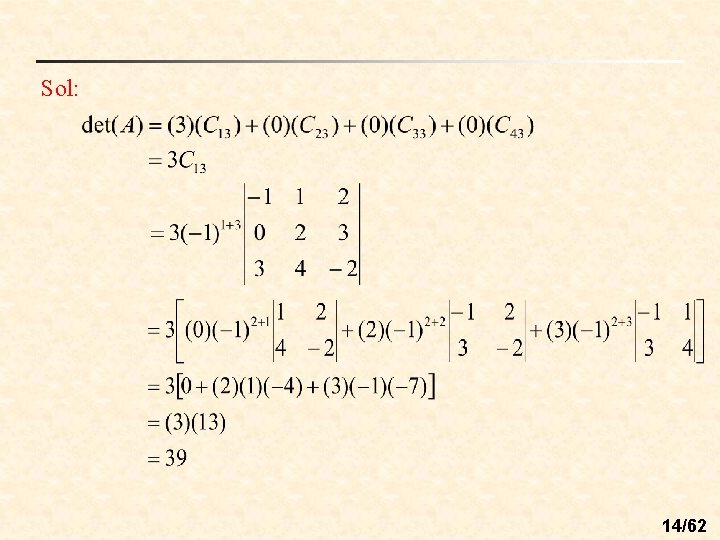
Sol: 14/62

n The determinant of a matrix of order 3: Subtract these three products. Add these three products. 15/62
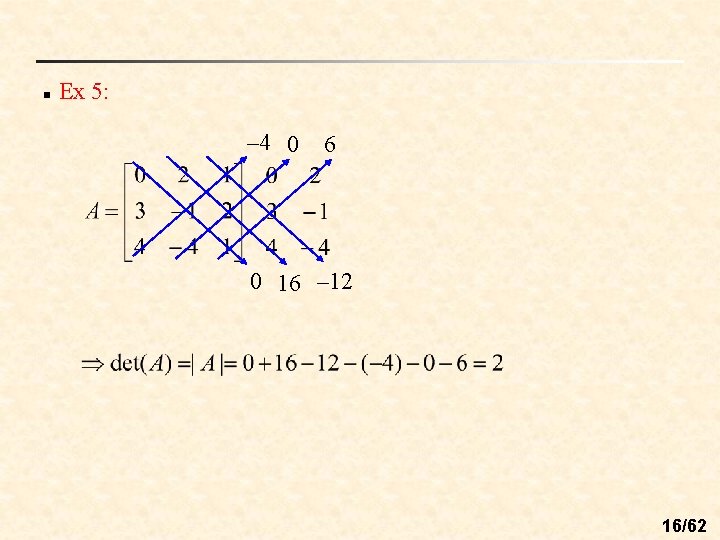
n Ex 5: – 4 0 6 0 16 – 12 16/62

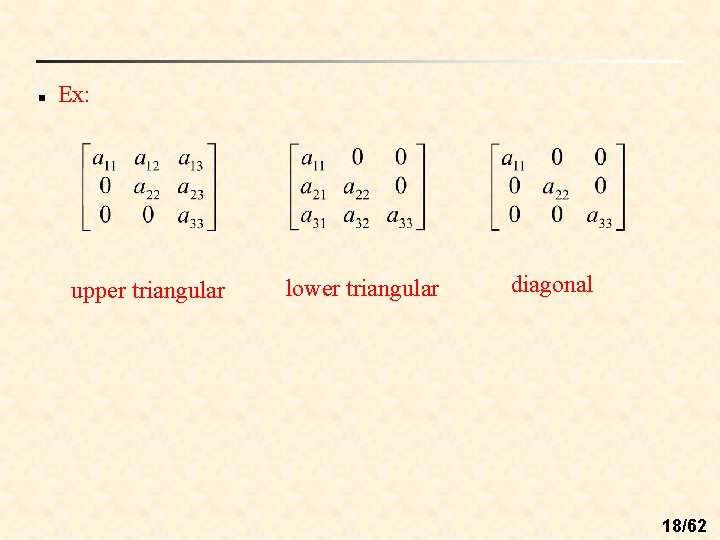
n Upper triangular matrix: All the entries below the main diagonal are zeros. n Lower triangular matrix: All the entries above the main diagonal are zeros. n Diagonal matrix: All the entries above and below the main diagonal are zeros. n Note: A matrix that is both upper and lower triangular is called diagonal. 17/62

n Ex: upper triangular lower triangular diagonal 18/62

n Thm 3. 2: (Determinant of a Triangular Matrix) If A is an n × n triangular matrix (upper triangular, lower triangular, or diagonal), then its determinant is the product of the entries on the main diagonal. That is 19/62

n Ex 6: Find the determinants of the following triangular matrices. (a) (b) Sol: (a) |A| = (2)(– 2)(1)(3) = – 12 (b) |B| = (– 1)(3)(2)(4)(– 2) = 48 20/62


3. 2 Evaluation of a determinant using elementary operations n Thm 3. 3: (Elementary row operations and determinants) Let A and B be square matrices. 22/62
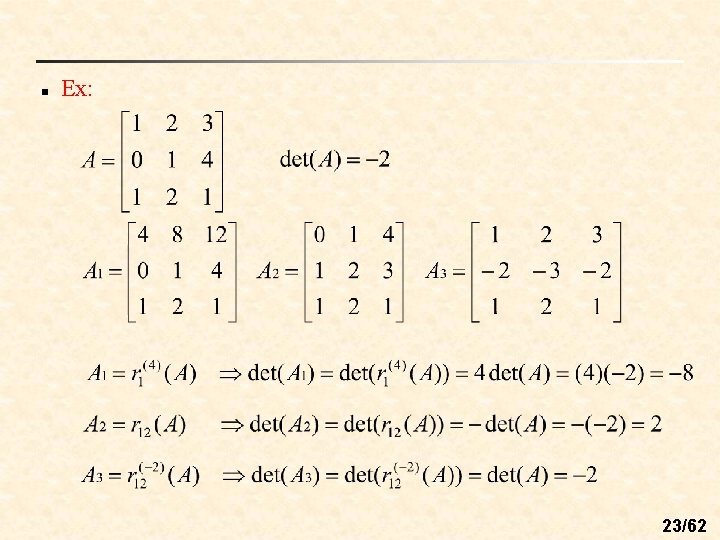
n Ex: 23/62

n Notes: 24/62

Note: A row-echelon form of a square matrix is always upper triangular. Ex 2: (Evaluation a determinant using elementary row operations) n Sol: 25/62
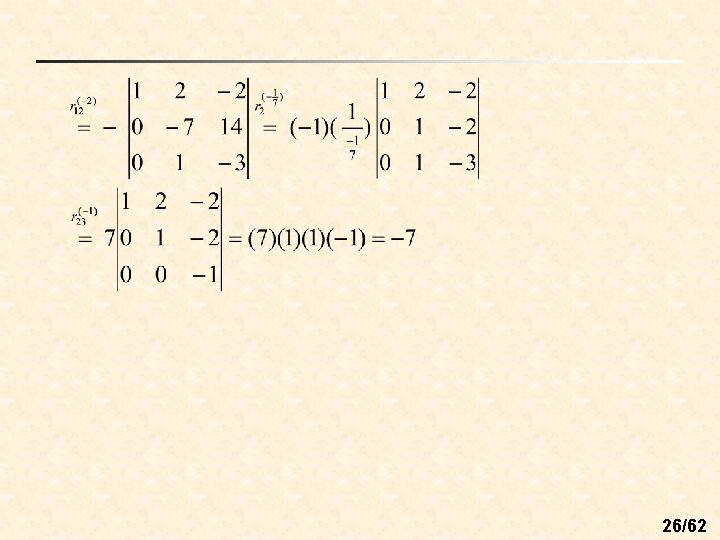
26/62
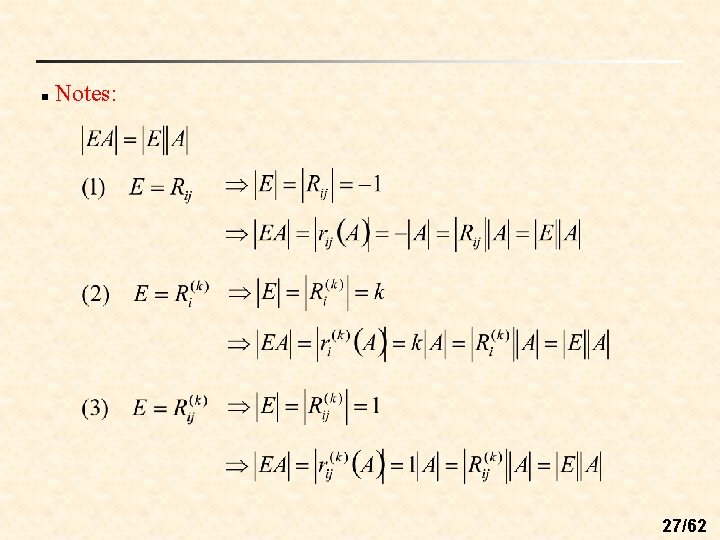
n Notes: 27/62

n Determinants and elementary column operations n Thm: (Elementary column operations and determinants) Let A and B be square matrices. 28/62
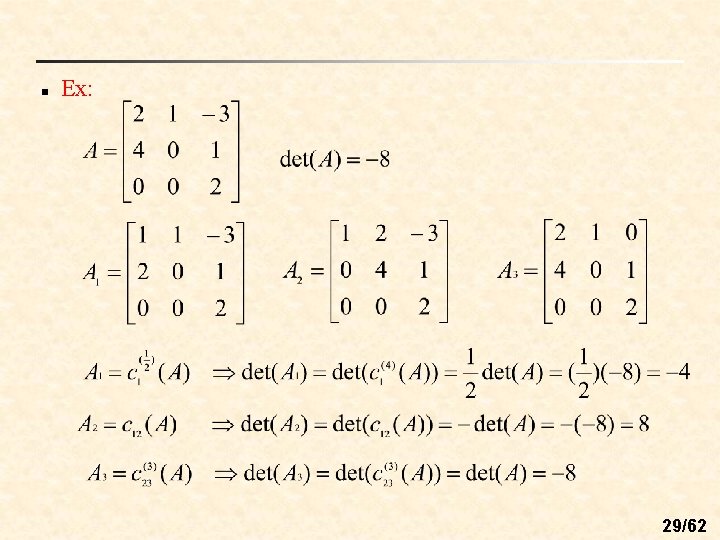
n Ex: 29/62

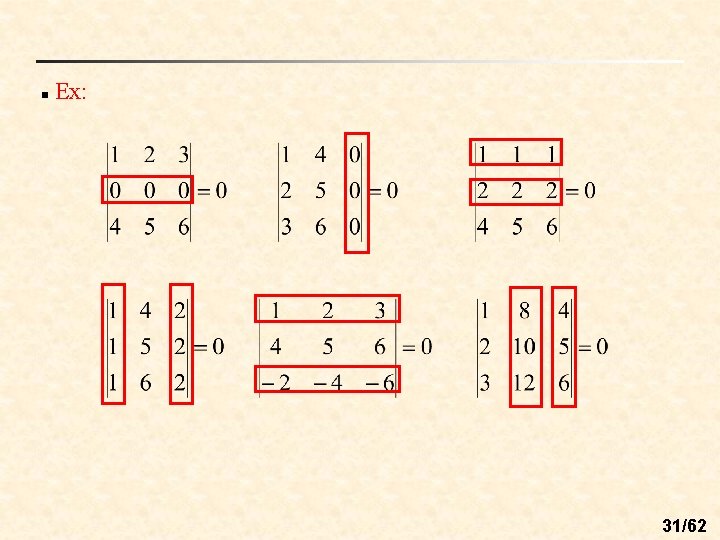
n Thm 3. 4: (Conditions that yield a zero determinant) If A is a square matrix and any of the following conditions is true, then det (A) = 0. (a) An entire row (or an entire column) consists of zeros. (b) Two rows (or two columns) are equal. (c) One row (or column) is a multiple of another row (or column). 30/62

n Ex: 31/62

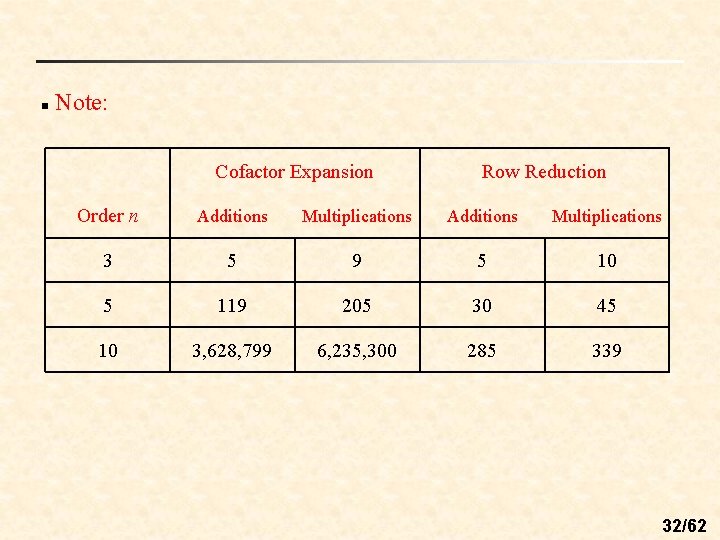
n Note: Cofactor Expansion Row Reduction Order n Additions Multiplications 3 5 9 5 10 5 119 205 30 45 10 3, 628, 799 6, 235, 300 285 339 32/62

n Ex 5: (Evaluating a determinant) Sol: 33/62

n Ex 6: (Evaluating a determinant) Sol: 34/62

35/62

3. 3 Properties of Determinants n Thm 3. 5: (Determinant of a matrix product) det (AB) = det (A) det (B) n Notes: (1) det (EA) = det (E) det (A) (2) (3) 36/62

n Ex 1: (The determinant of a matrix product) Find |A|, |B|, and |AB| Sol: 37/62

n Check: |AB| = |A| |B| 38/62

Thm 3. 6: (Determinant of a scalar multiple of a matrix) n If A is an n × n matrix and c is a scalar, then det (c. A) = cn det (A) n Ex 2: Sol: Find |A|. 39/62

n Thm 3. 7: (Determinant of an invertible matrix) A square matrix A is invertible (nonsingular) if and only if det (A) 0 n Ex 3: (Classifying square matrices as singular or nonsingular) Sol: A has no inverse (it is singular). B has an inverse (it is nonsingular). 40/62

n Thm 3. 8: (Determinant of an inverse matrix) n Thm 3. 9: (Determinant of a transpose) n Ex 4: (a) (b) Sol: 41/62

n Equivalent conditions for a nonsingular matrix: If A is an n × n matrix, then the following statements are equivalent. (1) A is invertible. (2) Ax = b has a unique solution for every n × 1 matrix b. (3) Ax = 0 has only the trivial solution. (4) A is row-equivalent to In (5) A can be written as the product of elementary matrices. (6) det (A) 0 42/62

n Ex 5: Which of the following system has a unique solution? (a) (b) 43/62

Sol: (a) This system does not have a unique solution. (b) This system has a unique solution. 44/62

3. 4 Introduction to Eigenvalues n Eigenvalue problem: If A is an n n matrix, do there exist n 1 nonzero matrices x such that Ax is a scalar multiple of x? n Eigenvalue and eigenvector: A:an n n matrix :a scalar x: a n 1 nonzero column matrix Eigenvalue (The fundamental equation for the eigenvalue problem) Eigenvector 45/62

n Ex 1: (Verifying eigenvalues and eigenvectors) Eigenvalue Eigenvector 46/62

n n Question: Given an n n matrix A, how can you find the eigenvalues and corresponding eigenvectors? Note: (homogeneous system) If n has nonzero solutions iff . Characteristic equation of A Mn n: 47/62

n Ex 2: (Finding eigenvalues and eigenvectors) Sol: Characteristic equation: Eigenvalues: 48/62
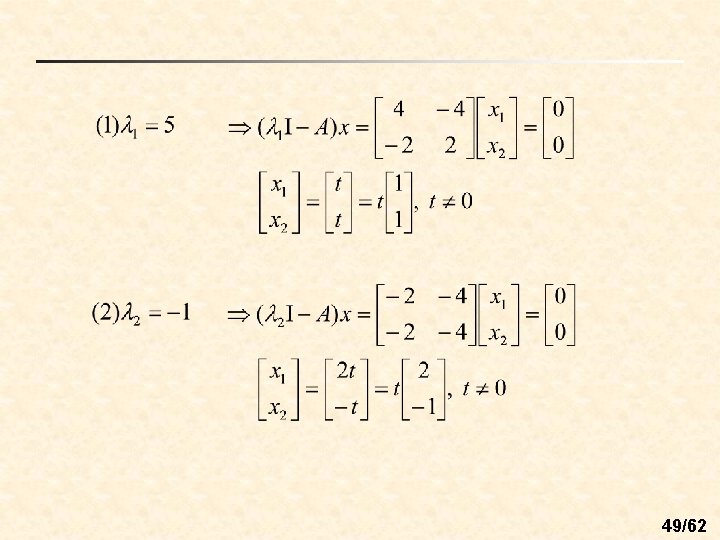
49/62

n Ex 3: (Finding eigenvalues and eigenvectors) Sol: Characteristic equation: 50/62

51/62

52/62

3. 4 Applications of Determinants n n Matrix of cofactors of A: Adjoint matrix of A: 53/62

n Thm 3. 10: (The inverse of a matrix given by its adjoint) If A is an n × n invertible matrix, then n Ex: 54/62

n Ex 1 & Ex 2: (a) Find the adjoint of A. (b) Use the adjoint of A to find Sol: 55/62
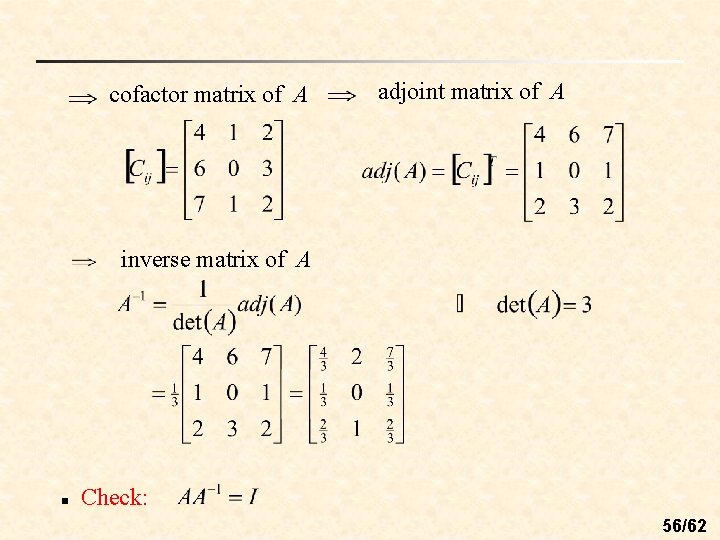
cofactor matrix of A adjoint matrix of A inverse matrix of A n Check: 56/62

n Thm 3. 11: (Cramer’s Rule) (this system has a unique solution) 57/62
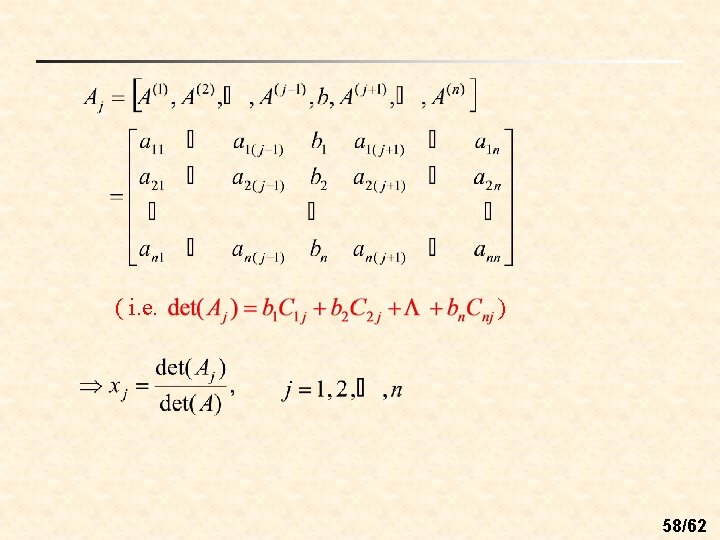
( i. e. ) 58/62
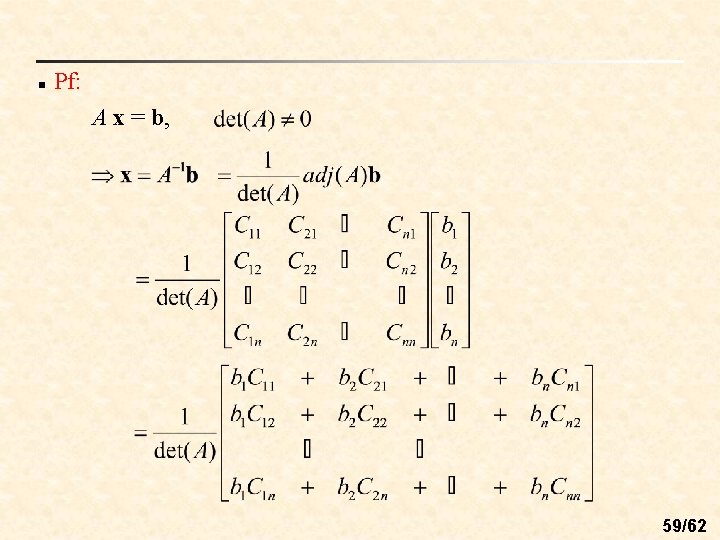
n Pf: A x = b, 59/62
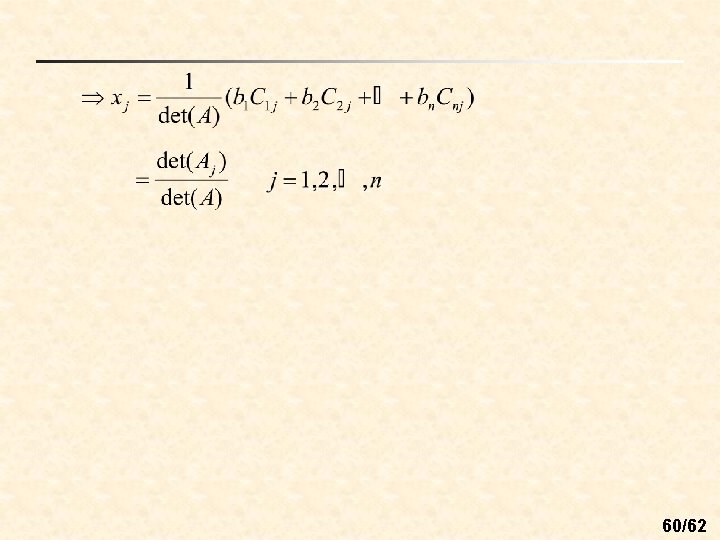
60/62

n Ex 4: Use Cramer’s rule to solve the system of linear equations. Sol: 61/62

Keywords in Section 3. 4: n matrix of cofactors : ﻣﺼﻔﻮﻓﺔ ﺍﻟﻤﻌﺎﻣﻼﺕ n adjoint matrix : ﻣﺼﻔﻮﻓﺔ ﻣﺼﺎﺣﺒﺔ n Cramer’s rule : ﻗﺎﻧﻮﻥ ﻛﺮﺍﻣﺮ 62/62
 Experiential readiness to learn example
Experiential readiness to learn example Chapter 16 determinants of the money supply
Chapter 16 determinants of the money supply Chapter 16 determinants of the money supply
Chapter 16 determinants of the money supply Chapter 16 determinants of the money supply
Chapter 16 determinants of the money supply Chapter 16 determinants of the money supply
Chapter 16 determinants of the money supply Equation du 1er degré
Equation du 1er degré Ar perceptual gap map
Ar perceptual gap map Determinantul unei matrice
Determinantul unei matrice Determinant properties
Determinant properties Peer culture
Peer culture Cliques and crowds
Cliques and crowds Matricws
Matricws What is a matrix
What is a matrix Matrices formula
Matrices formula Yarı simetrik matris
Yarı simetrik matris Determinants
Determinants Kolme tundmatuga võrrandisüsteem
Kolme tundmatuga võrrandisüsteem Matrix multiplication inverses and determinants
Matrix multiplication inverses and determinants How to find the inverse of 3 by 3 matrix
How to find the inverse of 3 by 3 matrix Tersinir matris
Tersinir matris How to evaluate the determinant
How to evaluate the determinant Determinant formula
Determinant formula Determinants of gait
Determinants of gait Nom determinant
Nom determinant Os perceptual gap map
Os perceptual gap map 3×3 matrices
3×3 matrices Notation for determinant of a matrix
Notation for determinant of a matrix Expanding along r1
Expanding along r1 Cardinality in math
Cardinality in math Determinant in excel
Determinant in excel Determinant formula
Determinant formula Cramer's rule 3 by 3 matrix
Cramer's rule 3 by 3 matrix How to evaluate the determinant of a matrix
How to evaluate the determinant of a matrix Matrix division
Matrix division Matrice transposée
Matrice transposée Determinant of matrix matlab
Determinant of matrix matlab Matrix inversion formula
Matrix inversion formula Determinants formula
Determinants formula Determinant gap map
Determinant gap map Negation partitif
Negation partitif Determinant symbol
Determinant symbol The most basic determinant of a person's wants and behavior
The most basic determinant of a person's wants and behavior Determinant gap map
Determinant gap map Determinant significat
Determinant significat The most basic determinant of a person's wants and behavior
The most basic determinant of a person's wants and behavior Definisi determinan matriks
Definisi determinan matriks Cofactor expansion example
Cofactor expansion example дискримінант
дискримінант Orthogonal matrix definition
Orthogonal matrix definition Qu est ce qu un determinant
Qu est ce qu un determinant Matrix inverse worksheet
Matrix inverse worksheet Finding determinant of a 3x3 matrix
Finding determinant of a 3x3 matrix Determinant of investment
Determinant of investment Hình ảnh bộ gõ cơ thể búng tay
Hình ảnh bộ gõ cơ thể búng tay Ng-html
Ng-html Bổ thể
Bổ thể Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Chó sói
Chó sói Thang điểm glasgow
Thang điểm glasgow Bài hát chúa yêu trần thế alleluia
Bài hát chúa yêu trần thế alleluia Các môn thể thao bắt đầu bằng tiếng nhảy
Các môn thể thao bắt đầu bằng tiếng nhảy Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới