Chapter 2 Determinants The Determinant Function The 2

Chapter 2 Determinants

The Determinant Function – The 2 2 matrix is invertible if ad-bc 0. The expression adbc occurs so frequently that it has a name; it is called the determinant of the matrix A and is denoted by the symbol det(A). – We want to obtain the analogous formula to square matrices of higher order.

Cofactor Expansion: Cramer's Rule • Minors and Cofactors – det(A)=a 11 a 22 a 33+a 12 a 23 a 31+a 13 a 21 a 32 -a 13 a 22 a 31 -a 12 a 21 a 33 a 11 a 23 a 32 =a 11(a 22 a 33 -a 23 a 32)-a 12(a 21 a 33 -a 23 a 31)+a 13(a 21 a 32 a 22 a 31) =a 11 M 11 -a 12 M 12+a 13 M 13 where – Definition: If A is a square matrix, then the minor of entry aij is denoted by Mij and is defined to be the determinant of the submatrix that remains after the ith row and jth column are deleted from A. The number (-1)i+j. Mij is denoted by Cij and is called the cofactor of entry aij. • Example: Finding Minors and Cofactors

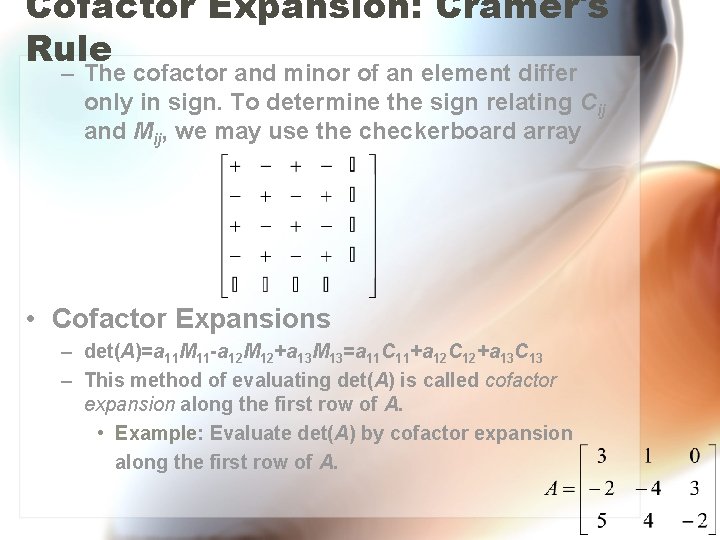
Cofactor Expansion: Cramer's Rule – The cofactor and minor of an element differ only in sign. To determine the sign relating Cij and Mij, we may use the checkerboard array • Cofactor Expansions – det(A)=a 11 M 11 -a 12 M 12+a 13 M 13=a 11 C 11+a 12 C 12+a 13 C 13 – This method of evaluating det(A) is called cofactor expansion along the first row of A. • Example: Evaluate det(A) by cofactor expansion along the first row of A.

Cofactor Expansion: Cramer's Rule – Theorem: The determinant of an n n matrix A can be computed by multiplying the entries in any row(or column) by their cofactors and adding the resulting products; that is, for each i i n and 1 j n, • Example: Cofactor expansion along the first column – Cofactor expansion and row or column operations can sometimes be used in combination to provide an effective method for evaluating determinant. • Example: Evaluate det(A) where

Cofactor Expansion: Cramer's Rule • Adjoint of a Matrix – If we multiply the entries in any row by the corresponding cofactors from a different row, the sum of these products is always zero. (This result also holds for columns) • Example: Find a 11 C 31+a 12 C 32+a 13 C 33 for – Definition: If A is an n n matrix and Cij is the cofactor of aij, then the matrix is called the matrix of cofactors from A. The transpose of this matrix is called the adjoint of A is denoted by adj(A).

Cofactor Expansion: Cramer's Rule – Example: Find the adjoint of A where – Theorem: If A is an invertible matrix, then • Example: Find the inverse of A in last example. • Cramer's Rule – be of marginal interest for computational purposes, but is useful for studying the mathematical properties of a solution without the need for solving the system

Cofactor Expansion: Cramer's Rule – Theorem: If Ax=b is a system of n linear equations in n unknowns such that det(A) 0, then the system has a unique solution. This solutions is where Aj is the matrix obtained by replacing the entries in the jth column of A by the entries in the matrix Example: Use Cramer's rule to solve

Cramer’s Rule • Solution • Therefore,

Evaluating Determinants by Row Reduction • A Basic Theorem – • Theorem: Let A be a square matrix. (a) If A has a row of zeros or a column of zeros, then det(A)=0. (b) det(A) = det(AT). • It is evident from (b) that every theorem about determinants that contains the word “row” is also true when the word “column” is substituted. Triangular Matrices – Theorem: If A is an n n triangular matrix(upper triangular, lower triangular, or diagonal), then det(A) is the product of the entries on the main diagonal of the matrix; that is, det(A)=a 11 a 22. . . ann. • Example: Find the determinant of

Evaluating Determinants by Row Reduction • Elementary Row Operations – • Theorem: Let A be an n n matrix. (a) If B is the matrix that results when a single row or single column of A is multiplied by a scalar k, then det(B)=k det(A). (b) If B is the matrix that results when two rows or two columns of A are interchanged, then det(B) = -det(A). (c) If B is the matrix that results when a multiple of one row of A is added to another row or when a multiple of one column is added to another column, then det(B) = det(A). Elementary Matrices – Theorem: Let E be an n n elementary matrix. (a) If E results from multiplying a row of In by k, then det(E) = k. (b) If E results from interchanging two rows of In, then det(E) = -1. (c) If E results from adding a multiple of one row of In to another, then det(E)=1.

Evaluating Determinants by Row Reduction • Matrices with Proportional Rows or Columns – Theorem: If A is a square matrix with two proportional rows or two proportional columns, then det(A) = 0. • Evaluating Determinants by Row Reduction – Idea: to reduce the given matrix to upper triangular form by elementary row operations, then compute the determinant of the upper triangular matrix, then relate that determinant to that of the original matrix – Example: Evaluate det(A) where – The method is well suited for computer evaluation since it is systematic and easily programmed.

Properties of the Determinant Function • Basic Properties of Determinants – Let A and B be n n matrices and k be any scalar. We have det(k. A)=kndet(A). – det(A+B) is usually not equal to det(A)+det(B). • Example: • Interesting example: – Theorem: Let A, B, and C be n n matrices that differ only in single row, say the rth, and assume that the rth row of C can be obtained by adding corresponding entries in the rth rows of A and B. Then det(C) = det(A) + det(B). The same result

Properties of the Determinant Function • Determinant of a Matrix Product – If A and B are square matrices of the same size, then det(AB)=det(A)det(B) – Lemma: If B is an n n matrix and E is an n n elementary matrix, then det(EB)=det(E)det(B). • Det(E 1 E 2. . . Er. B)=det(E 1)det(E 2). . . det(Er)det(B) • Determinant Test for Invertibility – Theorem: A square matrix A is invertible if and only if det(A) 0. – A square matrix with two proportional rows or columns is not invertible. – Theorem: If A and B are square matrices of the same size, then det(AB)=det(A)det(B).

Properties of the Determinant Function – Example: Verifying det(AB)=det(A)det(B) – Theorem: If A is invertible, then

Properties of the Determinant Function • Summary – Theorem: If A is an n n matrix, then the following are equivalent. (a)A is invertible. (b)Ax=0 has only the trivial solution. (c)The reduced row-echelon form of A is In. (d)A is expressible as a product of elementary matrices. (e)Ax=b is consistent for every n 1 matrix b. (f) Ax=b has exactly one solution for every n 1 matrix b. (g)det(A) 0.

The Determinant Function • Definition of a Determinant – By an elementary product from an n n matrix A we shall mean any product of n entries from A, no two of which come from the same row or same column.

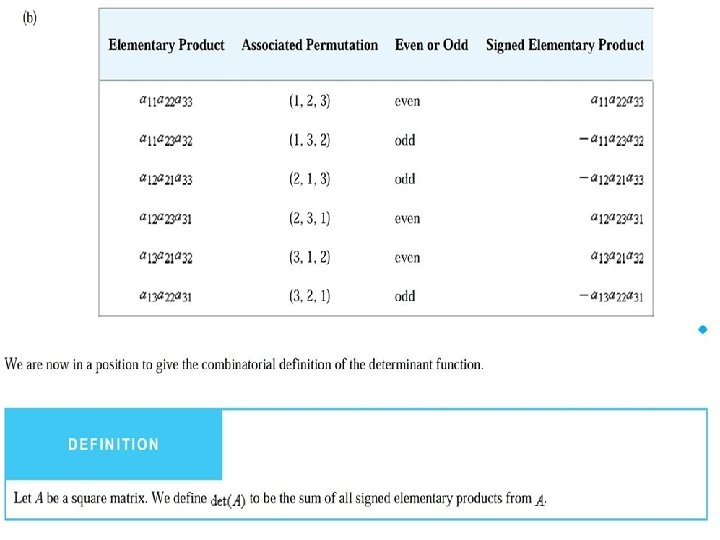
The Determinant Function • Example: List all elementary products from the matrices – An n n matrix A has n! elementary products of the form – signed elementary product from A: an elementary product multiplied by +1 or – 1. We use + if (j 1, j 2, . . . , jn) is an even permutation and the – if (j 1, j 2, . . . , jn) is an odd permutation. • Example: List all signed elementary products from the matrices

The Determinant Function • Definition: Let A be a square matrix. The determinant function is denoted by det, and we define det(A) to be the sum of all signed elementary products from A. The number det(A) is called the determinant of A. • Example: Find the determinants of matrices – mnemonic method(only for 2 2 and 3 3 matrices) • Example: Evaluate the determinants of

The Determinant Function • Notation and Terminology – The symbol |A| is an alternative notation for det(A). – Although the determinant of a matrix is a number, it is common to use the term “determinant” to refer to the matrix whose determinant is being computed. – The determinant of A is often written symbolically as – Evaluating determinants directly from the definition leads to computational difficulties.