Chapter 2 Determinants Determinant of a 3 3

Chapter 2 Determinants

Determinant of a 3× 3 matrix can be computed by the following short cut. a 1 a 2 a 3 b 1 b 2 b 3 c 1 c 2 c 3 i. e. - - a 1 a 2 b 1 b 2 c 1 c 2 + + + a 1 b 2 c 3 + a 2 b 3 c 1 + a 3 b 1 c 2 – a 3 b 2 c 1 – a 1 b 3 c 2 – a 2 b 1 c 3 There are 6 terms to add/subtract, because 3× 2× 1 = 6.

Determinant of a 4× 4 matrix Let be a 4× 4 matrix then det(A) = Each is a permutation of the set {1, 2, 3, 4}. In other words : {1, 2, 3, 4} is a one-to-one onto function. sgn( ) is the sign of , which will be either + or - , and will be defined on the next slide.

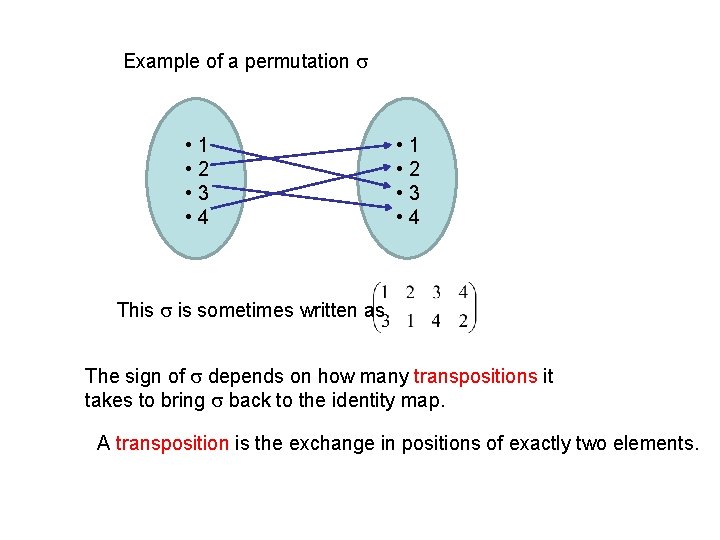
Example of a permutation • 1 • 2 • 3 • 4 This is sometimes written as The sign of depends on how many transpositions it takes to bring back to the identity map. A transposition is the exchange in positions of exactly two elements.

Example of a transposition (1, 2, 3, 4) (3, 2, 1, 4) It is not hard to see that exactly the two elements 1 , 3 exchange positions. Let’s go back to the previous example = (3, 1, 4, 2), Ans: 3 How many swaps can bring back to (1, 2, 3, 4)? The number of transpositions is not unique, but the parity of the number of transpositions is unique. If the number of transpositions is even, then sgn( ) = +, otherwise sgn( ) = –

Recall that det(A) = and because the summation includes all possible permutations, there will be 4! = 24 terms in the sum. Exactly half of the permutations are even, and half are odd. Each term in the sum (without the sign) is a product of exactly 1 element from each row and exactly 1 element from each column of the matrix A.

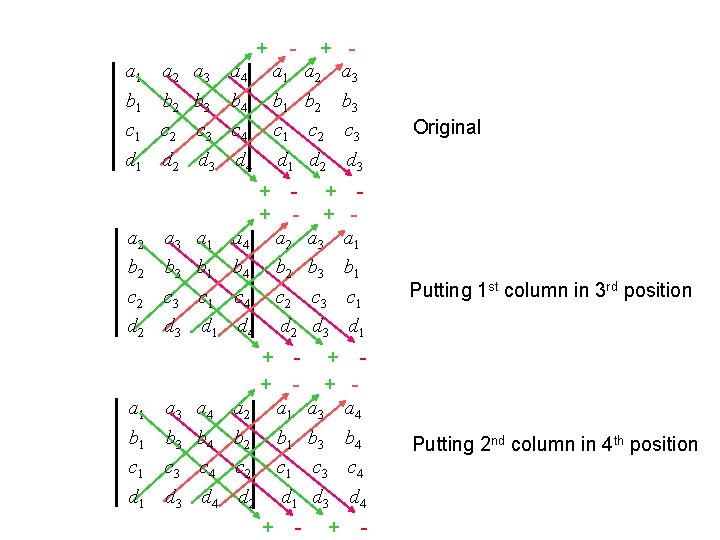
Determinant of a 4× 4 matrix cannot be computed by the similar short cut, + a 1 a 2 a 3 a 4 b 1 b 2 b 3 b 4 c 1 c 2 c 3 c 4 d 1 d 2 d 3 d 4 + - + a 1 a 2 a 3 b 1 b 2 b 3 c 1 c 2 c 3 d 1 d 2 d 3 - + - because this will only generate 8 terms. In a 4× 4 determinant, there should be 4× 3× 2× 1 = 24 terms. (i. e. we get only 1/3 of all ) Where are the other 16 terms?

+ a 1 a 2 a 3 a 4 b 1 b 2 b 3 b 4 c 1 c 2 c 3 c 4 d 1 d 2 d 3 d 4 + a 1 a 2 a 3 b 1 b 2 b 3 c 1 c 2 c 3 d 1 d 2 d 3 + + a 2 a 3 a 1 a 4 b 2 b 3 b 1 b 4 c 2 c 3 c 1 c 4 d 2 d 3 d 1 d 4 + + a 1 a 3 a 4 a 2 b 1 b 3 b 4 b 2 c 1 c 3 c 4 c 2 d 1 d 3 d 4 d 2 + - + + a 2 a 3 a 1 b 2 b 3 b 1 c 2 c 3 c 1 d 2 d 3 d 1 Original - + + a 1 a 3 a 4 b 1 b 3 b 4 c 1 c 3 c 4 d 1 d 3 d 4 Putting 1 st column in 3 rd position - - + - Putting 2 nd column in 4 th position

2. 1 The Determinant Function The determine is a function that associates every square matrix with a number called the determinant of A, denoted by det(A). Definition: For a 2× 2 matrix , if then det(A) = ad – bc Properties: The determinant function satisfies the following. (a) det(In) = 1 (b) If B is obtained from A by interchanging any two rows, then det(B) = –det(A). (c) If B is obtained from A by adding a multiple of one row to another, then det(B) = det(A). (d) If B is obtained from A by multiplying a number m to a row of A, then det(B) = m det(A)

Theorem: If is a diagonal matrix, then det(D) = d 11 d 22 …dnn Theorem: If A is a triangular matrix (either upper or lower), then det(A) is also the product of its diagonal elements, det(A) = a 11 a 22 …ann

2. 2 Properties of Determinants Theorem: If two rows of a square matrix A are the same, then det(A) = 0. Corollary: If all elements in one row of a square matrix A are zero then det(A) = 0. Theorem: A square matrix is invertible if and only if det(A) ≠ 0, and in this case det(A-1) = 1/det(A) Theorem: If A and B are both n×n matrices, then det(AB) = det(A)det(B) Warning: det(A + B) is NOT equal to det(A) + det(B) in general.

Theorem: If A is an n×n matrix and AT is its transpose, then det(AT) = det(A)

Block Triangular Matrices A square matrix A is said to be in block triangular form if it can be partitioned as where P and Q are square matrices. In this case det(A) = det(P) det(S) Note: In general, even if A can be partitioned as Where P, Q, R and S are all square matrices, it is not true that

Important Note: In general, even if A can be partitioned as where P, Q, R and S are all square matrices, it is not true that det(A) = det(P)det(S) – det(Q)det(R)

Block Diagonal Matrices A square matrix A is said to be in block diagonal form if it can be partitioned as where P, Q, and R are all square matrices, and the other elements in A are all zeros. In this case, det(A) = det(P) det(Q) det(R)

2. 3 Signed Elementary products Definition: A permutation of a set of integers is a reordering of those integers without omissions or repetitions. (another definition: A permutation of a set S of integers is a one-to-one onto function from S to itself. Example: There are 6 permutations of the set {1, 2, 3} namely, (1, 2, 3), (2, 1, 3), (3, 1, 2), (1, 3, 2), (2, 3, 1), (3, 2, 1) Remark: In general, if a set S has n elements, then there are n! many permutations of S.

Definition: An inversion occurs in a permutation (j 1, j 2, …, jn) whenever a larger number precedes a smaller one. A permutation is called even if it has an even number of inversions, and it is called odd if it has an odd number of inversions. Definition: An elementary product from a n×n matrix A is a product of n entries from A, exactly one from each row and one from each column. Example: If A is a 4× 4 matrix then a 12 a 23 a 31 a 44 is an elementary product. In general, an elementary product is of the form where (j 1, j 2, … , jn) is a permutation of the set {1, 2, … , n}

Definition: A signed elementary product is an elementary product multiply by +1 or -1 depending on whether the permutation (j 1, j 2, … , jn) is even or odd. More precisely, we have (1) if (j 1, j 2, … , jn) is even (2) if (j 1, j 2, … , jn) is odd. Theorem: The any square matrix A, det(A) is the sum of all signed elementary products from A. Remark: For an n×n matrix, there are n! many elementary products, hence this is not an efficient way to compute the determinant of the matrix when n is large.

2. 4 Cofactor Expansion; Cramer’s Rule Definition: Given an n×n matrix A (a) The (i, j)-th minor of A, denoted by Mij , is the determinant of the (n - 1)×(n - 1) matrix obtained by deleting the i-th row and the j-th column of A. (b) The (i, j)-th cofactor of A, denoted by Cij , is (-1)i+j Mij Example:

Evaluating the Determinant by “Expansion by Cofactors” Theorem: Let A be an n×n matrix. Then det(A) can be computed by the following ways. (1) Expanding by cofactors along any row, i. e. det(A) = ai 1 Ci 1 + ai 2 Ci 2 + · · · +ain. Cin where 1 ≤ i ≤ n (2) Expanding by cofactors along any column, i. e. det(A) = a 1 j. C 1 j + a 2 j. C 2 j + · · · +anj. Cnj where 1 ≤ j ≤ n Note: This method is still very inefficient. The best practical method is to use the following two elementary row operations, (continued on next page)

(1) exchange two rows, or (2) add a multiple of a certain row to another row to transform the matrix A into a upper (or lower) triangular matrix, and then multiply all the diagonal elements together. However, remember to multiply the determinant by -1 whenever two rows of the matrix are interchanged.

The Adjoint and a Theoretical Formula for A– 1 Definition: If A is an n×n matrix, the adjoint of A, denoted by adj(A), is the transpose of the matrix of cofactors, Theorem: If A is an n×n matrix, then A× adj(A) = (det. A) In Thus if det(A) ≠ 0, A– 1 exists and

Cramer’s Rule Let AX = B be a system of n linear equations in n unknowns, where det(A) ≠ 0. The unique solution to this system is given by where etc.