AUTOVALORES AUTOVETORES TRANSFORMAES LINEARES E ANLISE MODAL Ettore















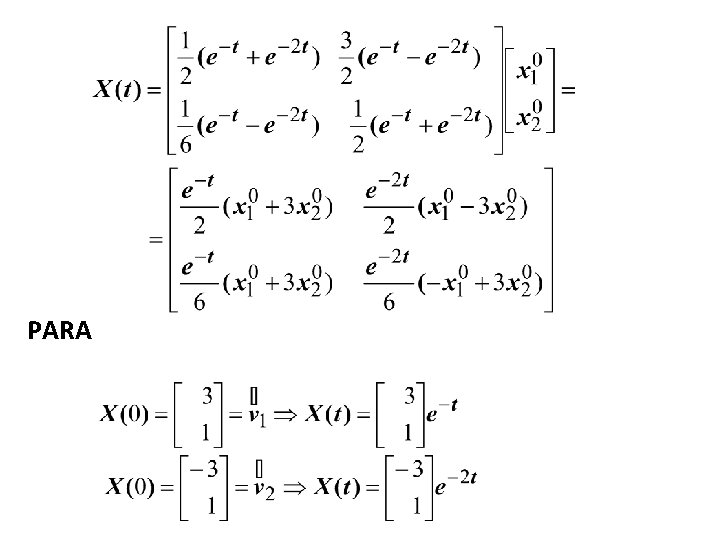
![EXEMPLOS DE TRAJETÓRIAS NO ESPAÇO DE ESTADOS FONTE: REFERÊNCIA [2] EXEMPLOS DE TRAJETÓRIAS NO ESPAÇO DE ESTADOS FONTE: REFERÊNCIA [2]](https://slidetodoc.com/presentation_image_h2/761b494824800dacb606c597807ab1ed/image-18.jpg)
![EXEMPLOS DE TRAJETÓRIAS NO ESPAÇO DE ESTADOS FONTE: REFERÊNCIA [2] EXEMPLOS DE TRAJETÓRIAS NO ESPAÇO DE ESTADOS FONTE: REFERÊNCIA [2]](https://slidetodoc.com/presentation_image_h2/761b494824800dacb606c597807ab1ed/image-19.jpg)
![EXEMPLOS DE TRAJETÓRIAS NO ESPAÇO DE ESTADOS FONTE: REFERÊNCIA [2] EXEMPLOS DE TRAJETÓRIAS NO ESPAÇO DE ESTADOS FONTE: REFERÊNCIA [2]](https://slidetodoc.com/presentation_image_h2/761b494824800dacb606c597807ab1ed/image-20.jpg)



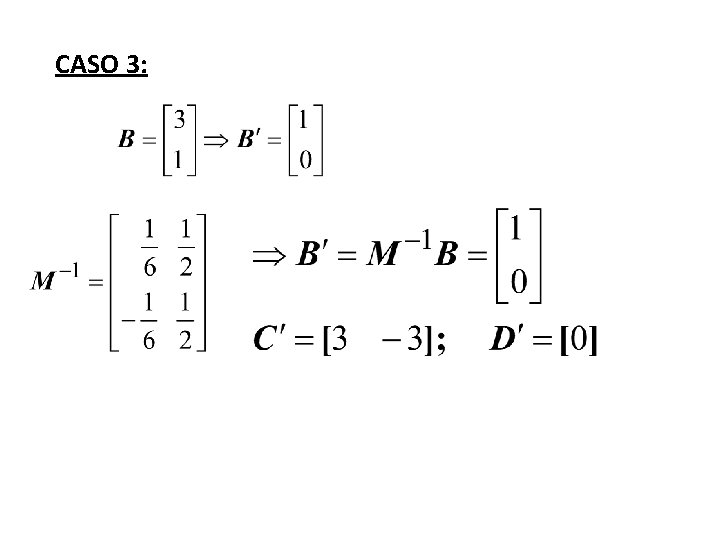





- Slides: 35

AUTO-VALORES, AUTO-VETORES TRANSFORMAÇÕES LINEARES E ANÁLISE MODAL Ettore A. de Barros

1. INTRODUÇÃO a-ESTADO ESTRUTURA MATEMÁTICA QUE REPRESENTA O COMPORTAMENTO DO SISTEMA DIN MICO. É COMPOSTO POR UM CONJUNTO DE VARIÁVEIS, TAL QUE SEU CONHECIMENTO NO INSTANTE t=t 0, E O CONHECIMENTO DA EXCITAÇÃO, NESTE MESMO INSTANTE, DETERMINA COMPLETAMENTE O COMPORTAMENTO DO SISTEMA. EXISTE UM CONJUNTO MÍNIMO DE VARIÁVEIS DE ESTADO QUE SE TORNA NECESÁRIO PARA REPRESENTAR O SISTEMA DE MODO PRECISO.

b- EQUAÇÃO DE ESTADOS c-ESPAÇO DE ESTADOS ESPAÇO n-DIMENSIONAL, CUJOS EIXOS CORRESPONDEM A

ANALISEMOS ALGUMAS PROPRIEDADES DA MATRIZ “A” E SUAS RELAÇÕES COM A RESPOSTA NATURAL DO SISTEMA DIN MICO E SUA REPRESENTAÇÃO NO ESPAÇO DE ESTADOS

2 - ANÁLISE DA EQUAÇÃO DE AUTO-VALORES E AUTO-VETORES DA MATRIZ “A”

CADA RAIZ DA EQUAÇÃO POLINOMIAL É UM AUTO-VALOR. PARA CADA VALOR DISTINTO, TEM-SE 1 AUTO-VETOR. O CONJUNTO DE AUTO-VETORES ASSIM FORMADO É LINEARMENTE INDEPENDENTE. SUPONHA O CASO DE A (nxn) COM “n” AUTO-VALORES DISTINTOS ENTRE SÍ. QUALQUER VETOR “X”, PODE SER EXPRESSO POR:

NA FORMA MATRICIAL, TEMOS: APLICANDO A EQUAÇÃO DE AUTO-VALORES, TEMOS: PASSANDO À FORMA MATRICIAL E APLICANDO 1), VEM:

DA EXPRESSÃO ANTERIOR, VEM:

3. APLICAÇÃO NA RESPOSTA NATURAL SABEMOS QUE DE 4), TEMOS:

APLICANDO 7) EM 6), VEM:

4. MODOS DO SISTEMA CHAMAMOS DE MODOS DO SISTEMA ÀS FUNÇÕES TEMPORAIS QUE FORMAM A SOLUÇÃO DE TEMOS OS SEGUINTES MODOS POSSÍVEIS

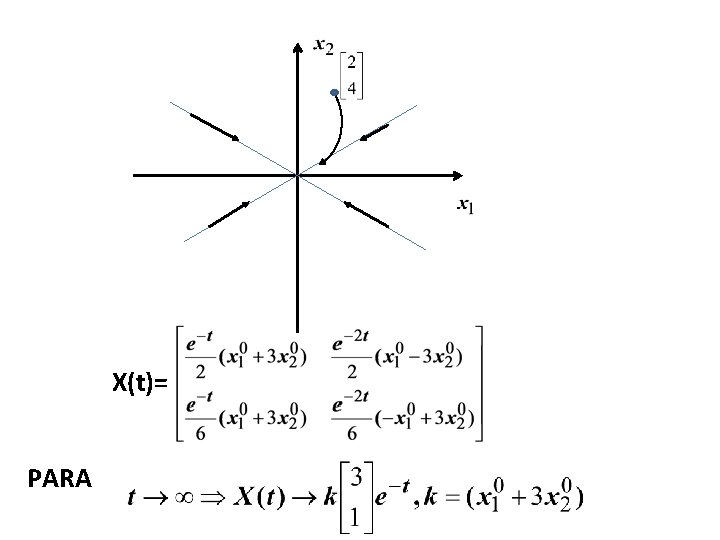
OS AUTO-VETORES RELACIONAM OS MODOS DO SISTEMA , QUE SÃO AS CARACTERÍSTICAS DE RESPOSTAS, COM A TRAJETÓRIA NO ESPAÇO DE ESTADOS. CONFORME SE APROXIMAM DA ORIGEM, AS TRAJETÓRIAS PASSAM A SER TANGENTES ÀS DIREÇÕES DOS AUTOVETORES. O MOVIMENTO NO ESPAÇO DE ESTADOS, AO LONGO DOS AUTO-VETORES, OCORRE COM INTENSIDADES DITADAS PELOS MODOS CORRESPONDENTES

EXEMPLO

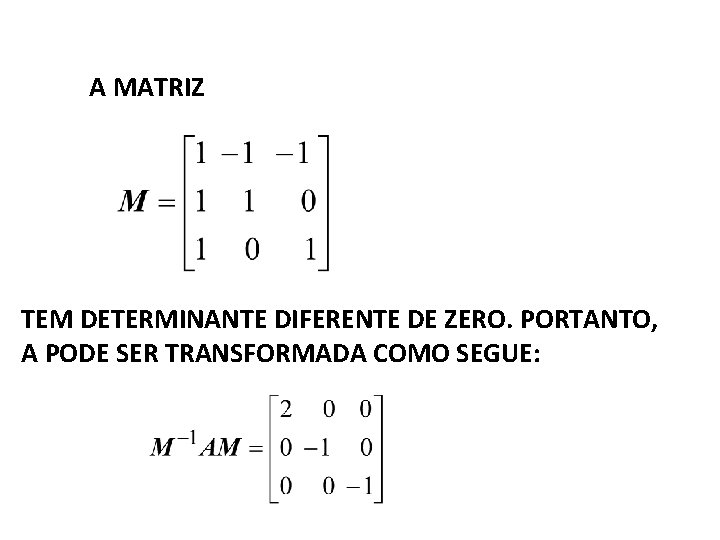
SEJAM SENDO ASSIM, A MATRIZ M É DADA POR

APLICAÇÃO À EXPRESSÃO DA RESPOSTA NATURAL:
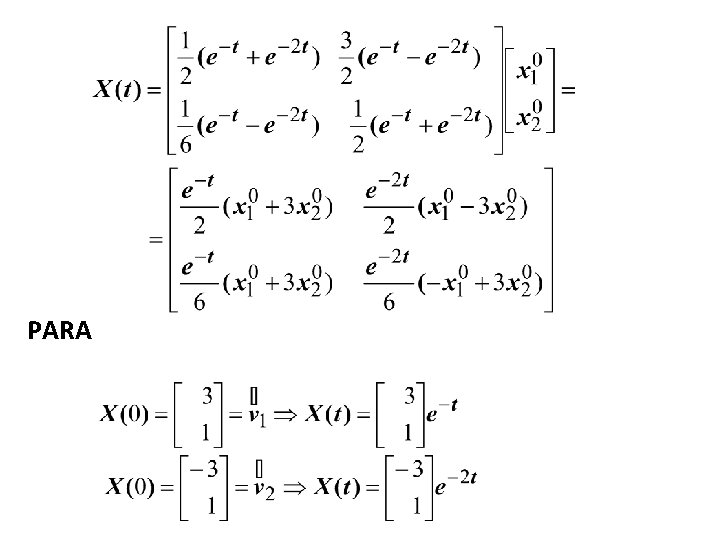
PARA

X(t)= PARA
![EXEMPLOS DE TRAJETÓRIAS NO ESPAÇO DE ESTADOS FONTE REFERÊNCIA 2 EXEMPLOS DE TRAJETÓRIAS NO ESPAÇO DE ESTADOS FONTE: REFERÊNCIA [2]](https://slidetodoc.com/presentation_image_h2/761b494824800dacb606c597807ab1ed/image-18.jpg)
EXEMPLOS DE TRAJETÓRIAS NO ESPAÇO DE ESTADOS FONTE: REFERÊNCIA [2]
![EXEMPLOS DE TRAJETÓRIAS NO ESPAÇO DE ESTADOS FONTE REFERÊNCIA 2 EXEMPLOS DE TRAJETÓRIAS NO ESPAÇO DE ESTADOS FONTE: REFERÊNCIA [2]](https://slidetodoc.com/presentation_image_h2/761b494824800dacb606c597807ab1ed/image-19.jpg)
EXEMPLOS DE TRAJETÓRIAS NO ESPAÇO DE ESTADOS FONTE: REFERÊNCIA [2]
![EXEMPLOS DE TRAJETÓRIAS NO ESPAÇO DE ESTADOS FONTE REFERÊNCIA 2 EXEMPLOS DE TRAJETÓRIAS NO ESPAÇO DE ESTADOS FONTE: REFERÊNCIA [2]](https://slidetodoc.com/presentation_image_h2/761b494824800dacb606c597807ab1ed/image-20.jpg)
EXEMPLOS DE TRAJETÓRIAS NO ESPAÇO DE ESTADOS FONTE: REFERÊNCIA [2]

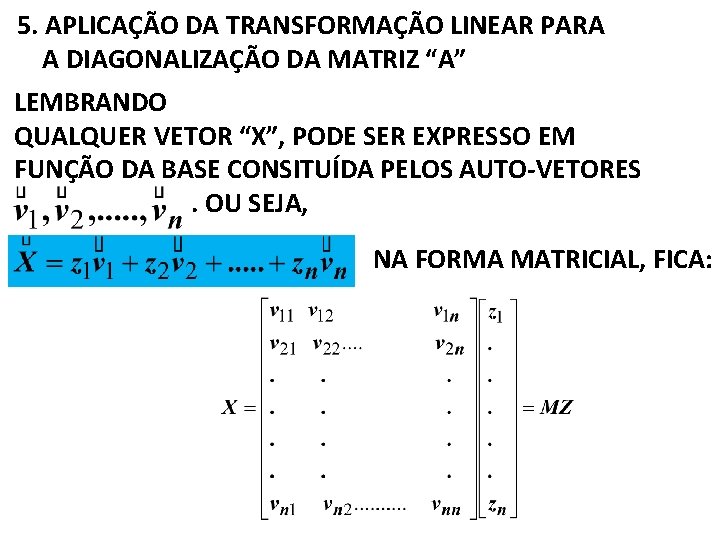
5. APLICAÇÃO DA TRANSFORMAÇÃO LINEAR PARA A DIAGONALIZAÇÃO DA MATRIZ “A” LEMBRANDO QUALQUER VETOR “X”, PODE SER EXPRESSO EM FUNÇÃO DA BASE CONSITUÍDA PELOS AUTO-VETORES. OU SEJA, NA FORMA MATRICIAL, FICA:

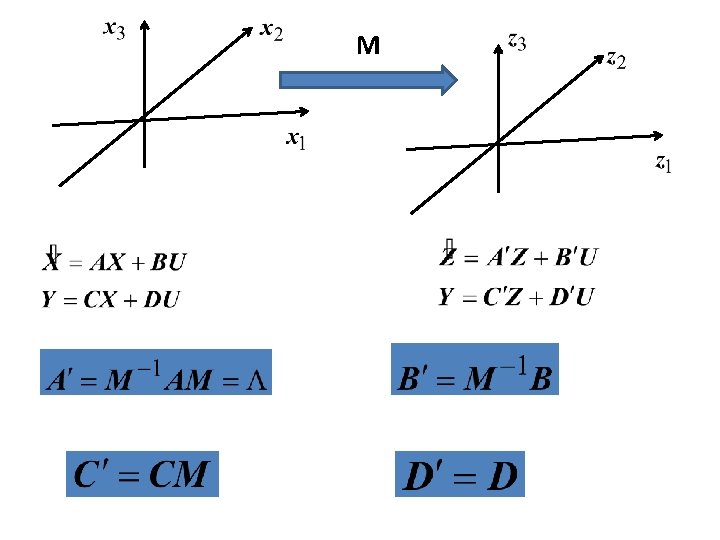
PORTANTO X=MZ APLICANDO NA EQUAÇÃO DE ESTADOS , VEM: SENDO ASSIM, OBTIVEMOS UMA NOVA REPRESENTAÇÃO DO MESMO SISTEMA DIN MICO:

M

ESSA É CONHECIDA COMO UMA TRANSFORMAÇÃO DE SIMILARIDADE ESSE TIPO DE TRANSFORMAÇÃO É UTILIZADO PARA TRANSFORMAR A MATRIZ “A” NUMA FORMA CONVENIENTE PARA A ANÁLISE E PROCESSAMENTO DO SISTEMA. NOTE QUE “P” PRECISA SER INVERTÍVEL, ENTRADA E SAÍDA NÃO SÃO ALTERADAS E UM NOVO CONJUNTO DE VARIÁVEIS DE ESTADO SURGE

APLICAÇÃO CASO 1:

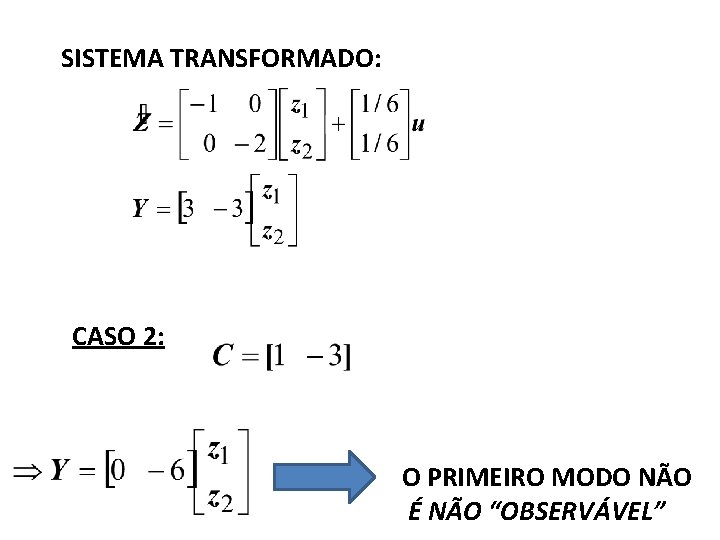
SISTEMA TRANSFORMADO: CASO 2: O PRIMEIRO MODO NÃO É NÃO “OBSERVÁVEL”
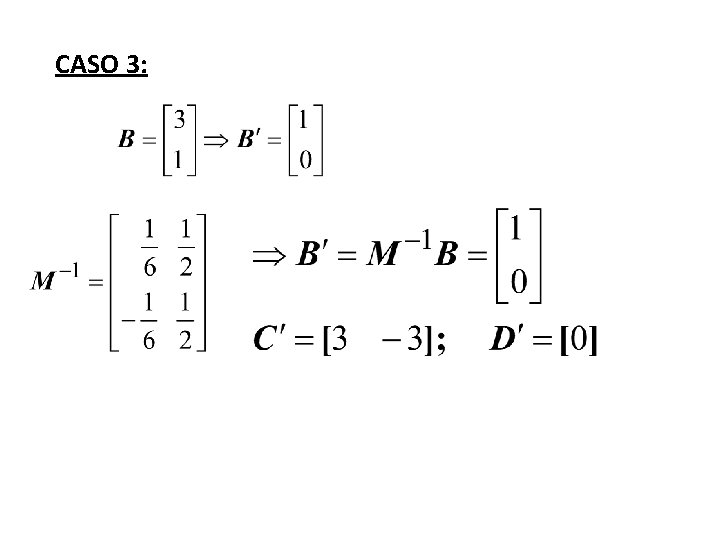
CASO 3:

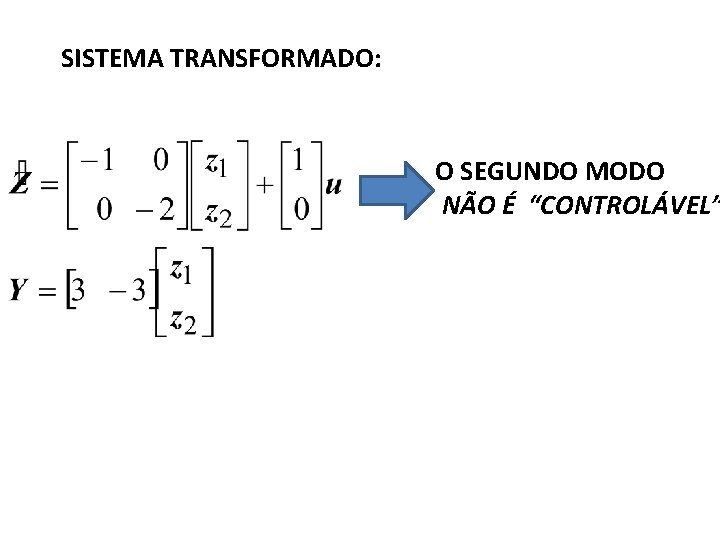
SISTEMA TRANSFORMADO: O SEGUNDO MODO NÃO É “CONTROLÁVEL”

CASO DE AUTO-VALORES COM MULTIPLICIDADE • SE ISSO CORRE, OS AUTO-VETORES PODEM NÃO SER L. I. *, O QUE IMPLICARIA NA IMPOSSIBILIDADE DE SE DIAGONALIZAR “A” • O MAIS PRÓXIMO QUE CONSEGUIRÍAMOS DE UMA MATRIZ DIAGONAL, NESSE CASO, É A “FORMA CANÔNICA DE JORDAN”

*HÁ CASOS EM QUE, MESMO COM AUTO-VALORES EM MULTIPLICIDADE, A MATRIZ PODE SER DIAGONALIZÁVEL. OU SEJA, A MATRIZ, MESMO ASSIM, POSSUI UM CONJUNTO DE AUTO-VETORES L. I. PARA O AUTO-VALOR IGUAL A “ 2”, O AUTO-VETOR PODE SER TOMADO COMO SENDO PARA O SEGUNDO AUTO-VALOR, A SOLUÇÃO GERAL PARA O AUTO-VETOR CORRESPONDENTE É DADA POR:

A MATRIZ TEM DETERMINANTE DIFERENTE DE ZERO. PORTANTO, A PODE SER TRANSFORMADA COMO SEGUE:

O QUE ACONTECE COM OS MODOS DO SISTEMA? EXEMPLO:

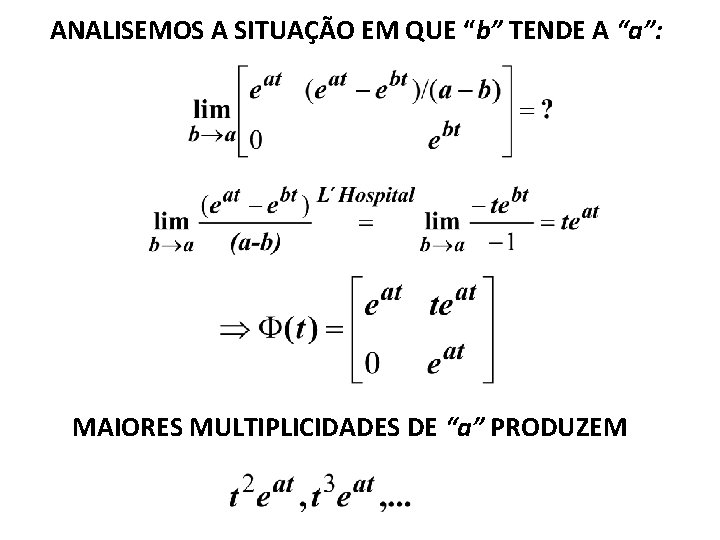
ANALISEMOS A SITUAÇÃO EM QUE “b” TENDE A “a”: MAIORES MULTIPLICIDADES DE “a” PRODUZEM

PODE-SE PRODUZIR A TRANSFORMAÇÃO DE SIMILARIDADE QUE LEVA A MATRIZ “A” À SUA FORMA CANÔNICA DE JORDAN. HÁ ALGORITMOS QUE FAZEM ESSA TAREFA: [V, J]=Jordan(A) (Matlab)

REFERÊNCIAS 1. Livro Texto 2. Control and Dynamic Systems. Y. Takahashi, D. M. Auslander, M. J. Rabins, D. M. 1972. Addison-Wesley. 3. Linear Systems. T. Kailath. Prentice-Hall. 1980. 4. Engenharia de Controle Moderno. 2ª. Edição. Prentice-Hall. 1990.
 Combinação linear de vetores
Combinação linear de vetores Anlise swot
Anlise swot O que é transformações químicas
O que é transformações químicas Autovalores
Autovalores Transformaes
Transformaes Teorema espectral
Teorema espectral Transformaes
Transformaes Sistemas lineares escalonamento
Sistemas lineares escalonamento Lineares gleichungssystem
Lineares gleichungssystem Regelungen
Regelungen Listas lineares
Listas lineares Sistemas lineares 2 ano ensino médio
Sistemas lineares 2 ano ensino médio Análise de sistemas lineares
Análise de sistemas lineares Quadratische funktionen im alltag
Quadratische funktionen im alltag Lineares significado
Lineares significado Biaya modal leverage dan struktur modal
Biaya modal leverage dan struktur modal Faedah atas modal perkongsian
Faedah atas modal perkongsian Sebab berlaku rekod tak lengkap
Sebab berlaku rekod tak lengkap Modal aktif dan modal pasif
Modal aktif dan modal pasif Semi modals
Semi modals Ettore majorana foundation
Ettore majorana foundation Iti majorana grugliasco
Iti majorana grugliasco Majorana bachelet
Majorana bachelet Gentile ettore serra
Gentile ettore serra Duello tra ettore e achille
Duello tra ettore e achille Si contesero il pomo di paride
Si contesero il pomo di paride Cesaris casalpusterlengo classi prime
Cesaris casalpusterlengo classi prime Liceo majorana desio
Liceo majorana desio Skylab genova
Skylab genova Istituto majorana seriate
Istituto majorana seriate Liceo desio spark
Liceo desio spark Ettore majorana scomparsa
Ettore majorana scomparsa Ettore ferrari franciulli
Ettore ferrari franciulli Ettore lanzarone
Ettore lanzarone Skylab desio
Skylab desio Eneide proemio
Eneide proemio