Transformaes Geomtricas Transformaes Lineares espelhamento P x y

Transformações Geométricas

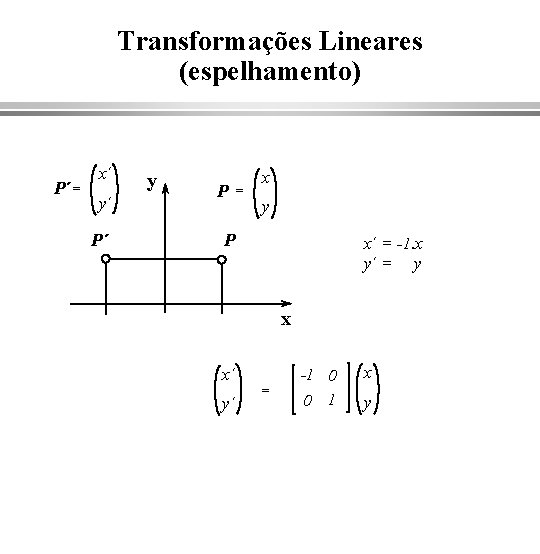
Transformações Lineares (espelhamento) P´ = x´ y´ P´ y P = x y P x´ = -1. x y´ = y x x´ y´ = -1 0 0 1 x y

Transformações Lineares (rotação) y x´ P´ = y´ P q = x x´ = x. cos q - y. sen q y´ = x. sen q + y. cos q y x x´ y´ = cos q sen q -sen q cos q x y

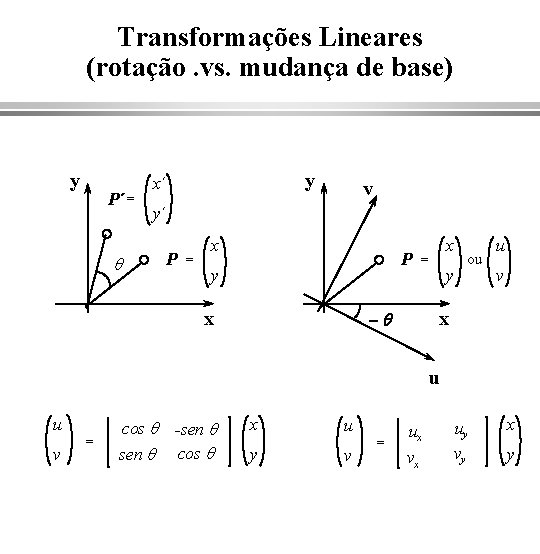
Transformações Lineares (rotação. vs. mudança de base) y P´ = y x´ v y´ P q = x P y = -q x x y ou u v x u u v = cos q sen q -sen q cos q x y u v = ux vx uy vy x y

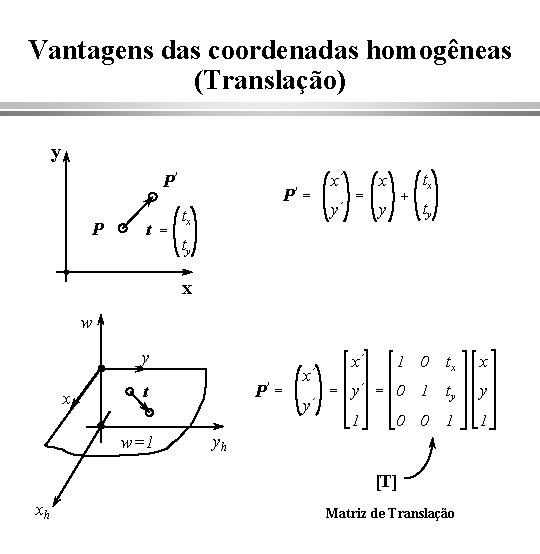
Vantagens das coordenadas homogêneas (Translação) y P’ P t = P’ = tx x’ y’ = x + y tx ty ty x w y x P’ = t w=1 x’ y’ x’ = 1 0 tx x y’ = 0 1 ty y 0 0 1 1 1 yh [T] xh Matriz de Translação

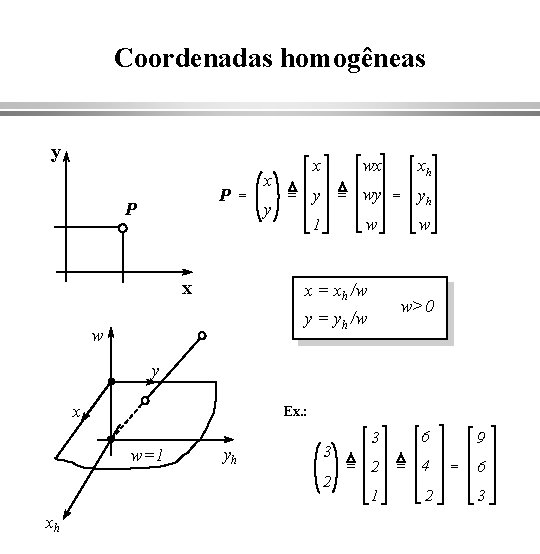
Coordenadas homogêneas y wx xh = wy = yh w w x P P x = x D = y y 1 D x = xh /w w>0 y = yh /w w y x Ex. : w=1 xh yh 3 3 D = 2 2 1 6 D = 4 2 9 = 6 3

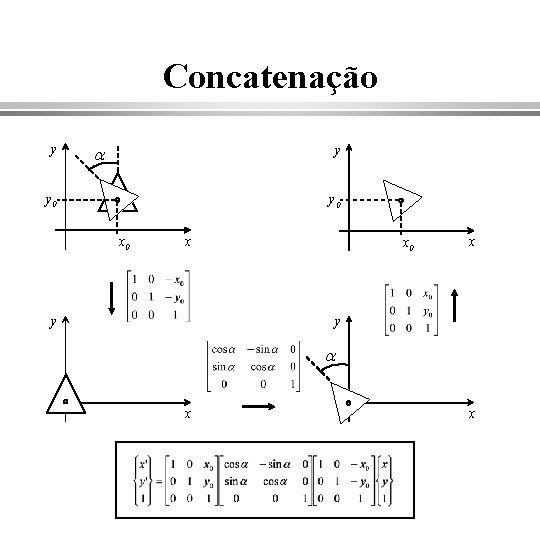
Concatenação y a y y 0 x 0 x y a x x

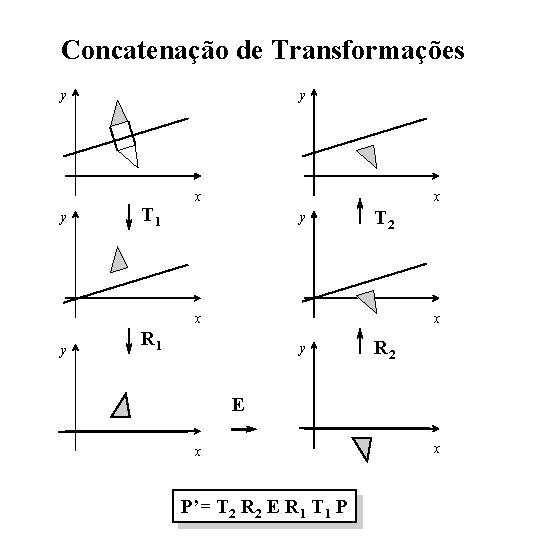
Concatenação de Transformações y y y T 1 x x y T 2 x y x R 1 y R 2 E x P’= T 2 R 2 E R 1 T 1 P x

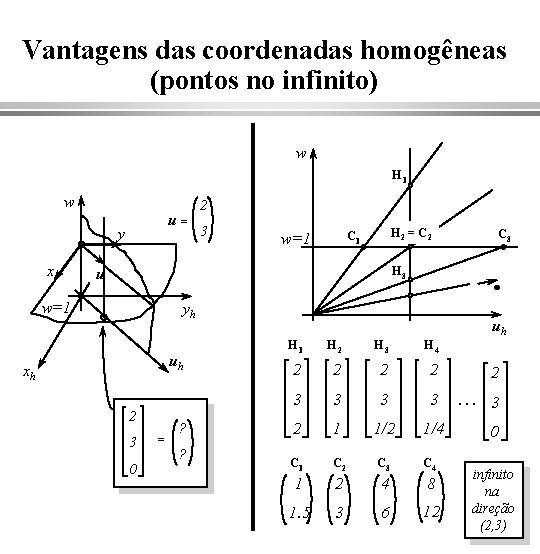
Vantagens das coordenadas homogêneas (pontos no infinito) w H 1 w u= y x 2 3 H 2 = C 2 C 1 w=1 C 3 H 3 u w=1 yh uh xh 2 3 0 = ? ? uh H 1 H 2 H 3 H 4 2 2 3 3 2 1 1/2 1/4 C 1 C 2 C 3 C 4 1 2 4 8 1. 5 3 6 12 2. . . 3 0 infinito na direção (2, 3)

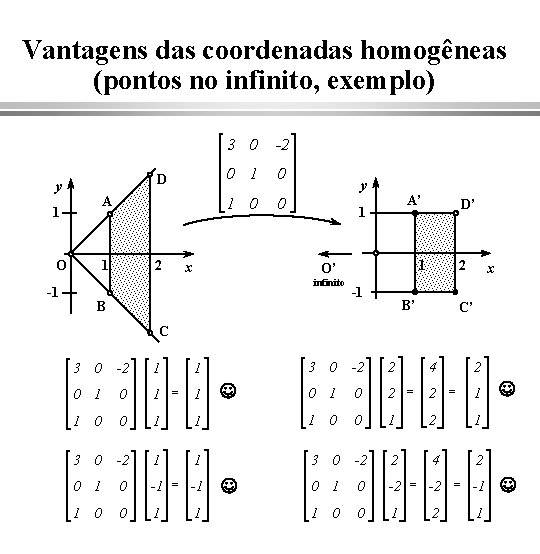
Vantagens das coordenadas homogêneas (pontos no infinito, exemplo) D y A 1 1 O -1 2 3 0 -2 0 1 0 0 x y A’ 1 1 O’ infinito B D’ -1 2 B’ x C’ C 3 0 -2 2 0 1 0 2 = 1 1 1 0 0 1 2 1 1 3 0 -2 2 4 2 0 1 0 -2 = -1 1 0 0 1 3 0 -2 1 1 0 1 = 1 1 0 0 1 3 0 -2 1 0 -1 = -1 1 0 0 1 1 J J 4 2 2 1 J J

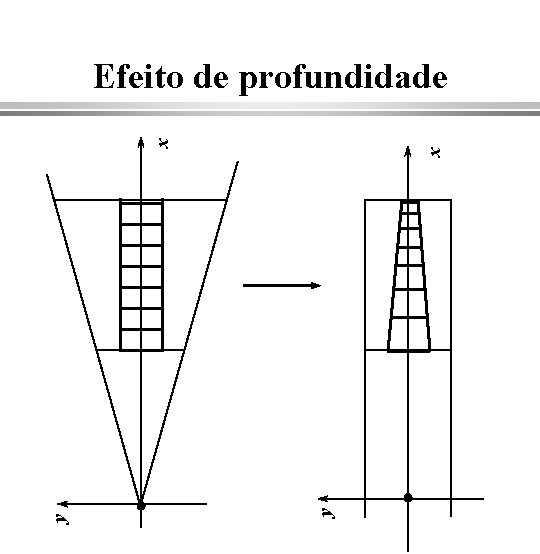
x y y x Efeito de profundidade

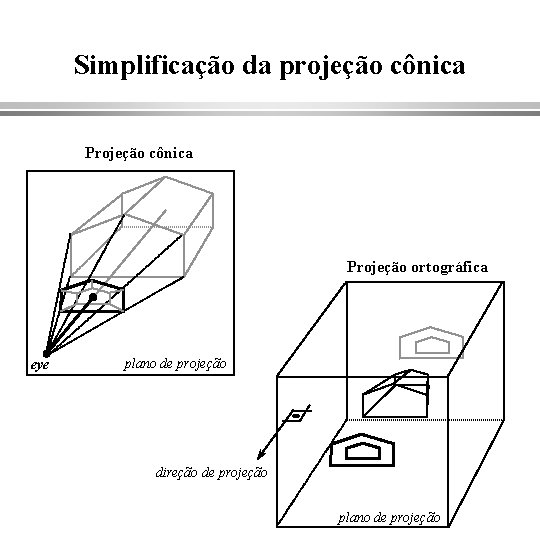
Simplificação da projeção cônica Projeção ortográfica eye plano de projeção direção de projeção plano de projeção

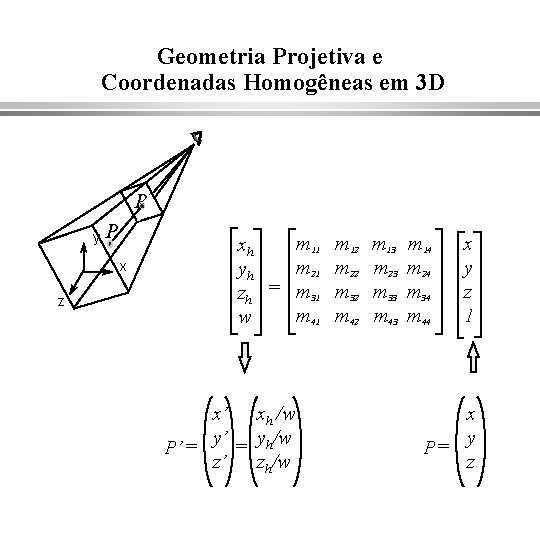
Geometria Projetiva e Coordenadas Homogêneas em 3 D P’ y P x z m 11 xh m 21 yh zh = m 31 m 41 w x’ xh /w y’ = yh/w P’ = z’ zh/w m 12 m 22 m 32 m 42 m 13 m 23 m 33 m 43 m 14 m 24 m 34 m 44 x y z 1 x y P= z

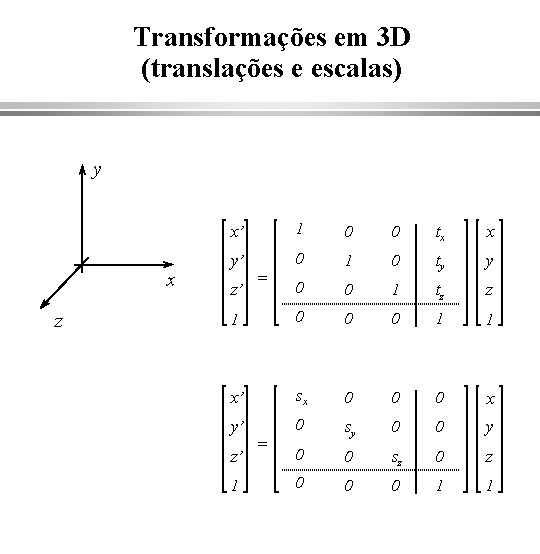
Transformações em 3 D (translações e escalas) y x z x’ 1 0 0 tx x y’ 0 1 0 ty y 0 0 1 tz z 1 0 0 0 1 1 x’ sx 0 0 0 x y’ 0 sy 0 0 sz 0 0 0 1 1 z’ z’ 1 = =

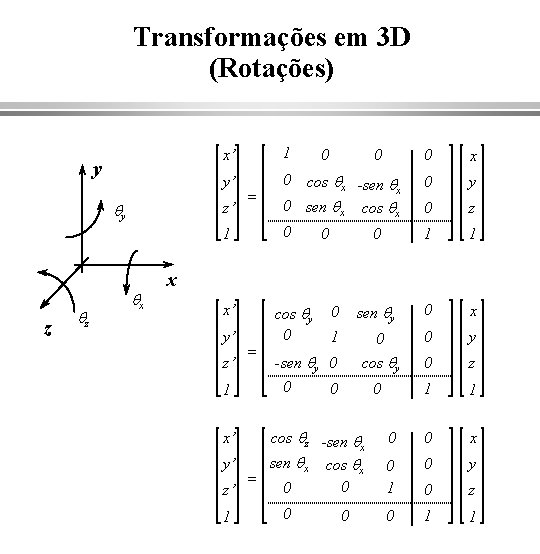
Transformações em 3 D (Rotações) y x’ 1 y’ 0 z’ qy = 1 z qz qx 0 0 cos qx -sen qx 0 sen qx cos qx 0 0 x 0 y 0 z 1 1 x x’ y’ z’ 1 = cos qy 0 0 sen qy 0 x 1 0 0 y cos qy 0 z 0 1 1 0 0 x 0 1 0 y 0 z 0 1 1 -sen qy 0 0 0 cos qz -sen qx cos qx y’ = 0 0 z’ 0 0 1 x’

Transformações em 3 D (rotação em torno de um eixo qualquer) x’ m 11 y’ m 21 z’ z = 1 m 12 m 13 0 x m 22 m 23 0 y m 31 m 32 m 33 0 z 0 0 0 1 1 v = (vx, vy, vz) y x m 11 m 12 m 13 m 21 m 22 m 23 m 31 m 32 m 22 = vx 2 + cosq (1 - vx 2) = vxvy(1 -cosq ) - vz sen q = vzvx(1 -cosq ) + vy sen q = vxvy(1 -cosq ) + vz sen q = vy 2 + cosq (1 - vy 2) = vyvz(1 -cosq ) - vx sen q = vxvz (1 -cosq ) - vy sen q = vyvz(1 -cosq )+ vx sen q = vz 2 + cosq (1 - vz 2)