ASI 3 Mthodes numriques pour lingnieur Rsolution de

ASI 3 Méthodes numériques pour l’ingénieur Résolution de systèmes d’équation non linéaires f(x)=0

Introduction • Comment résoudre le système suivant ? – Méthodes directes – Méthodes itératives

Introduction • Comment résoudre le système suivant ? – Méthodes directes : impossibles – Méthodes itératives

Résolution de f(x)=0 n • Soit une fonction f : R R n – continue sur. . . – Dérivable sur. . . • Principe : – trouver une méthode itérative uk+1 = g(uk) qui converge vers la solution

Résolution de f(x)=0 • Plusieurs méthodes – Newton – Quasi-Newton (sécante, Broyden, …) – Point fixe – Gradient • Problèmes ? – Convergence – Complexité

f(x)=0 lorsque n=1 • • Recherche par dichotomie méthode de la séquente méthode de point fixe méthode de Newton-Raphson } Aussi lorsque

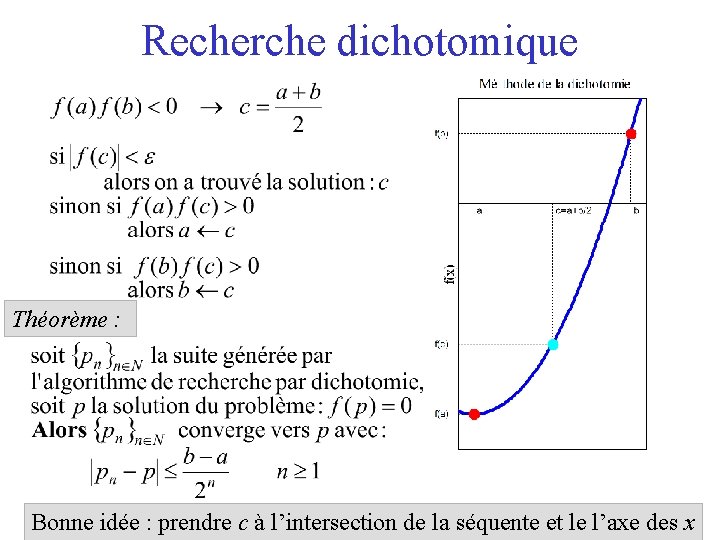
Recherche dichotomique Théorème : Bonne idée : prendre c à l’intersection de la séquente et le l’axe des x

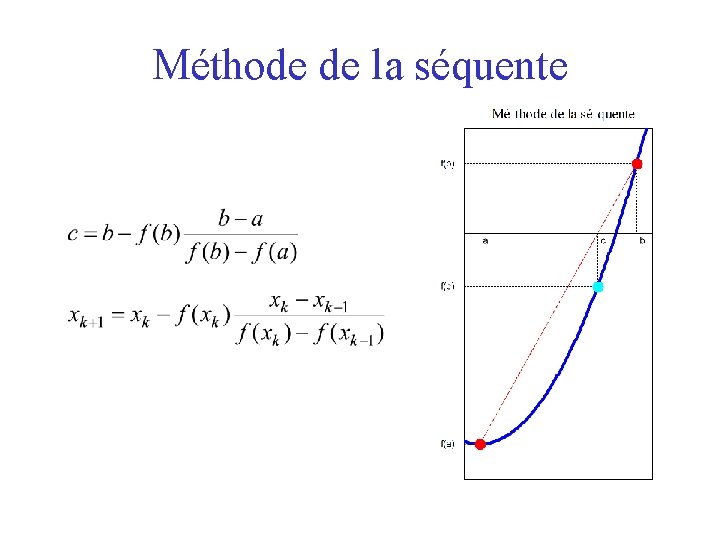
Méthode de la séquente

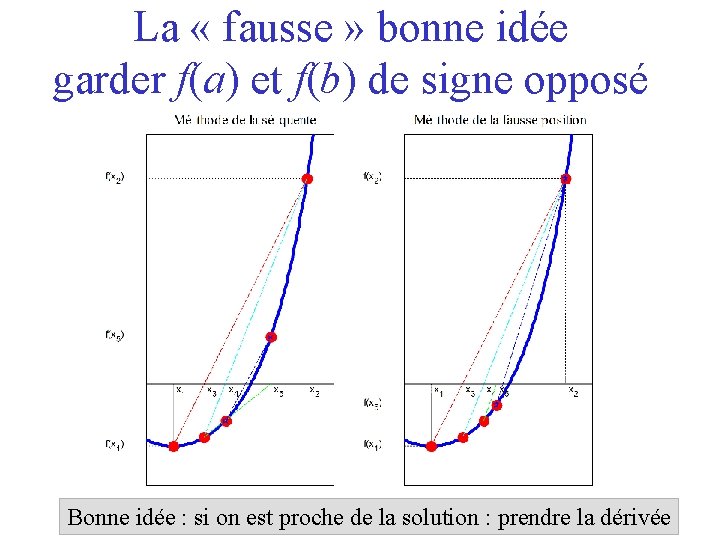
La « fausse » bonne idée garder f(a) et f(b) de signe opposé Bonne idée : si on est proche de la solution : prendre la dérivée

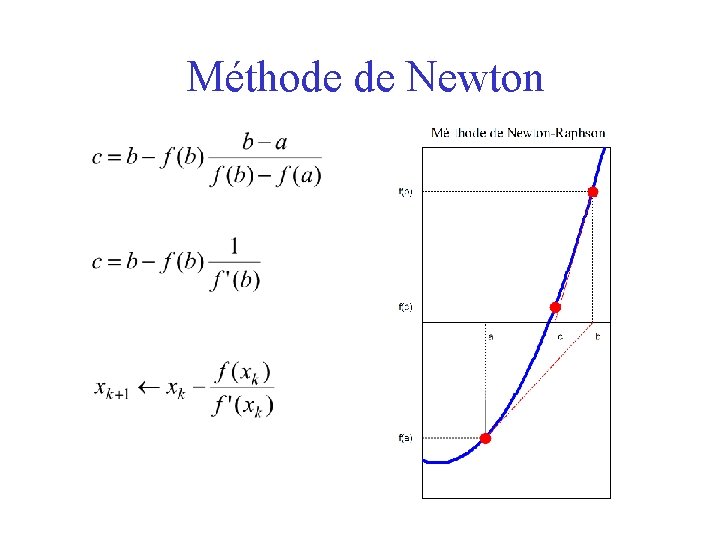
Méthode de Newton

Méthode de Newton • En dimension 1 : – on considère l'approximation affine : – on cherche h tel que f(uk+h)=0 soit si on néglige les terme en h 2 – et ainsi

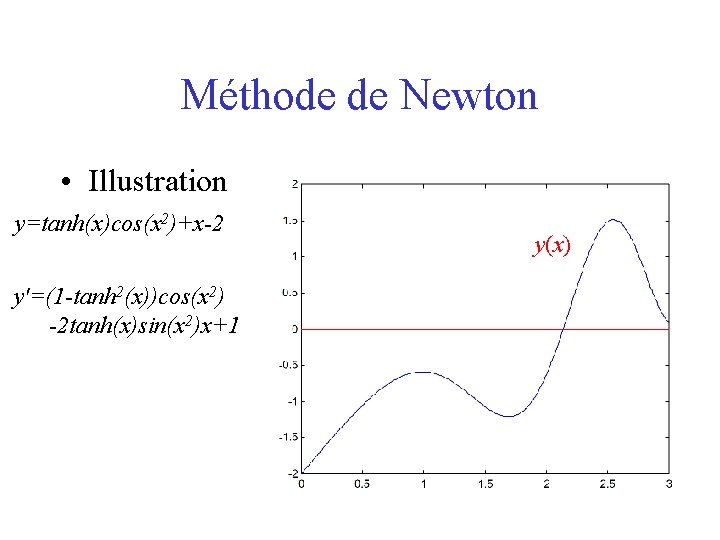
Méthode de Newton • Illustration y=tanh(x)cos(x 2)+x-2 y'=(1 -tanh 2(x))cos(x 2) -2 tanh(x)sin(x 2)x+1 y(x)

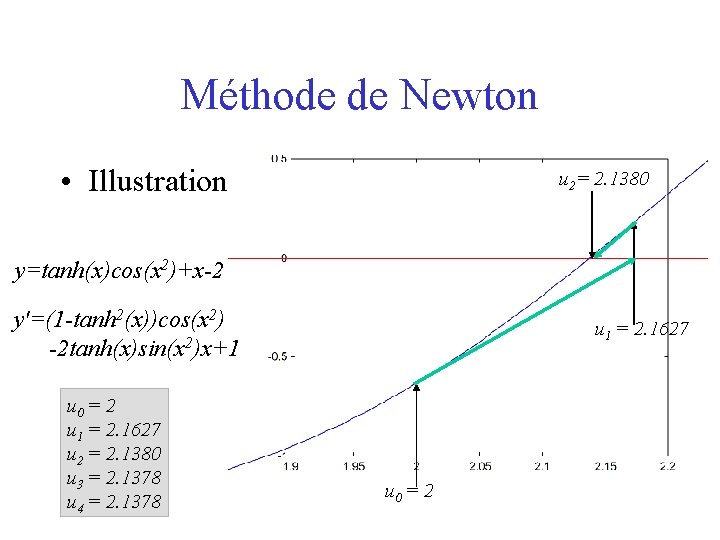
Méthode de Newton • Illustration u 2= 2. 1380 y=tanh(x)cos(x 2)+x-2 y'=(1 -tanh 2(x))cos(x 2) -2 tanh(x)sin(x 2)x+1 u 0 = 2 u 1 = 2. 1627 u 2 = 2. 1380 u 3 = 2. 1378 u 4 = 2. 1378 u 1 = 2. 1627 u 0 = 2

Méthode de point fixe • • • Définition f(x)=0 et le x = g(x) exemple convergence (suite de Cauchy) théorème de convergence globale théorème de convergence local – théorème du point fixe

Méthode du point fixe • Principe général : – trouver g en fonction de f telle que • f(û)=0 g(û)=û • la suite uk converge (si u 0 est bien choisi) – conditions suffisantes sur g en dimension 1 • g dérivable et |g'(û)| < 1 – conditions suffisantes sur g en dimension n • g différentiable et [ g(û)] < 1 ( = rayon spectral)

Méthode du point fixe • Convergence linéaire : – il existe C > 0 tel que • Inconvénient : choix de g de manière algébrique

Méthode du point fixe • Exemple en dimension 1 – résolution de x 2 - 2 = 0 – choix de g : • g 1(x) = 2/x • g 2(x) = 2 x - 2/x • g 3(x) = x/2 + 1/x g 1 u 0 = 1 u 1 = 2 u 2 = 1 u 3 = 2 u 4 = 1 g'1(x) = -2/x 2 g'1(x) = 2+2/x 2 g'1(x) = 1/2 -1/x 2 g 3 u 0 = 0. 999 u 1 = -0. 0402 u 2 = 49. 668 u 3 = 99. 296 u 4 = 198. 57 g'1(û) = -1 g'1(û) = 3 g'1(û) = 0 u 0 = 1 u 1 = 1. 5000 u 2 = 1. 4167 u 3 = 1. 4142 u 4 = 1. 4142 |g'(û)| < 1 convergence assurée

Méthode du point fixe • Exemple en dimension 1 – résolution de x 2 - 2 = 0 – choix de g : • g 1(x) = 2/x • g 2(x) = 2 x - 2/x • g 3(x) = x/2 + 1/x g 1 u 0 = 1 u 1 = 2 u 2 = 1 u 3 = 2 u 4 = 1 g'1(x) = -2/x 2 g'1(x) = 2+2/x 2 g'1(x) = 1/2 -1/x 2 g 3 u 0 = 0. 999 u 1 = -0. 0402 u 2 = 49. 668 u 3 = 99. 296 u 4 = 198. 57 g'1(û) = -1 g'1(û) = 3 g'1(û) = 0 u 0 = 1 u 1 = 1. 5000 u 2 = 1. 4167 u 3 = 1. 4142 u 4 = 1. 4142 |g'(û)| < 1 convergence assurée

résumé • Dichotomie • séquente • newton Multidimensionnel ? • Point fixe Accélération !

Accélération de la convergence • • • Définition : l’ordre de la convergence Motivation Définition du principe de Aitken Théorème de convergence quadratique Aitken et Steffensen

Méthode de Newton • En dimension n : – une équation, n inconnues : Le vecteur gradient – n équations, n inconnues : La matrice jacobienne La matrice Hessiène

Méthode de Newton • En dimension n : – on considère l'approximation affine : – on cherche h tel que f(uk+h)=0 soit système linéaire ! – et ainsi

Méthode de Newton • Théorème : – s'il existe û tel que • • f(û)=0 f est différentiable dans un voisinage de û f(û) est inversible – alors il existe > 0 tel que • si u° vérifie • alors la suite construite par la méthode de Newton converge vers û

Méthode de Newton • Avantage : convergence quadratique – il existe C > 0 tel que • Inconvénient : calcul de f(x) souvent difficile

Exemple

Méthodes de Quasi-Newton • Comment se passer du calcul de f(x) ? • En dimension 1 : méthode de la sécante Approximation de 1/f '(uk+1) • En dimension n : – le rapport précédent n'a aucun sens (u est un vecteur) – comment approcher f(uk+1) ?

Méthodes de Quasi-Newton • Approximation de f(uk+1) par la matrice Ak – Ak doit vérifier Ak(uk - uk-1)=f(uk) - f(uk-1) – Problème : il existe une infinité de Ak • Méthode de Broyden : – condition supplémentaire : Akz = Ak-1 z si (uk - uk-1)'z = 0

Méthodes de Quasi-Newton • Méthode de Broyden : algorithme – initialisation de u 0 et A 0 (différences finies) – itération :

Méthodes de Quasi-Newton • Convergence de la méthode de Broyden : – "super-linéaire" – moins rapide que Newton

Méthode du point fixe • Principe général : – trouver g en fonction de f telle que • f(û)=0 g(û)=û • la suite uk converge (si u 0 est bien choisi) – conditions suffisantes sur g en dimension 1 • g dérivable et |g'(û)| < 1 – conditions suffisantes sur g en dimension n • g différentiable et [ g(û)] < 1 ( = rayon spectral)

Méthode du point fixe • Exemple en dimension 3

Méthode du point fixe • Exemple en dimension 3

Méthode du point fixe • Exemple en dimension 3 (suite) – valeurs initiales (x 0=0. 1 ; y 0=0. 1 ; z 0=-0. 1) – – convergence vers (0. 5 ; 0. 0 ; -0. 5236) – résultat théorique: (0. 5 ; 0. 0 ; - /6)

Méthode du point fixe • Comment essayer d'accélérer la convergence – remplacer les valeurs par leurs "dernières" estimations • (cf. Gauss-Siedel pour les systèmes linéaires) – exemple :

Conclusion • Méthodes – Newton : • inconvénient = calcul des dérivées • avantage = convergence quadratique – Quasi-Newton : • inconvénient = convergence super-linéaire • avantage = plus de calcul des dérivées – Point Fixe : • inconvénient = convergence linéaire • inconvénient = choix de g • Problème général : initialisation de la suite !

TD • Implémenter en Matlab : – Newton, Broyden, point fixe (+Gauss Siedel) – pour les problèmes suivants : – comparer le temps de convergence (pour un même seuil)