ASI 3 Mthodes numriques pour lingnieur Optimisation 1

ASI 3 Méthodes numériques pour l’ingénieur Optimisation 1

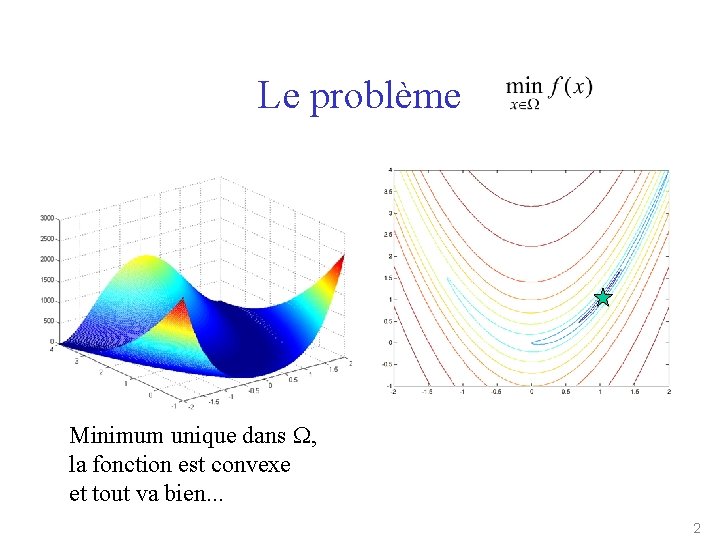
Le problème Minimum unique dans W, la fonction est convexe et tout va bien. . . 2

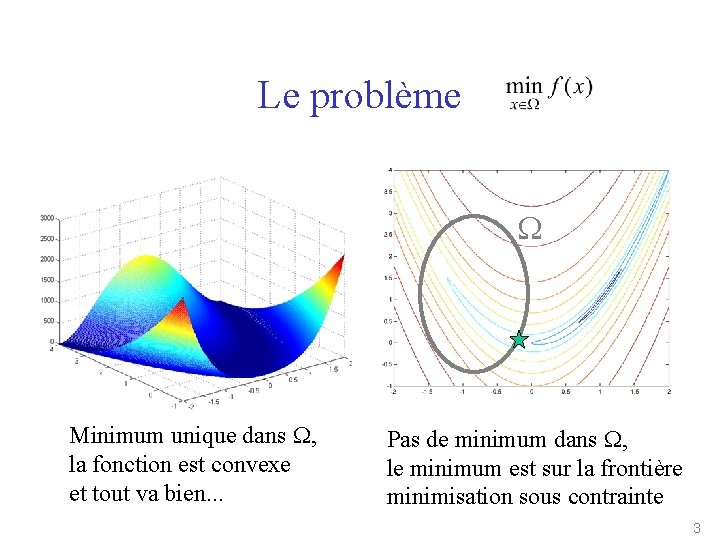
Le problème W Minimum unique dans W, la fonction est convexe et tout va bien. . . Pas de minimum dans W, le minimum est sur la frontière minimisation sous contrainte 3

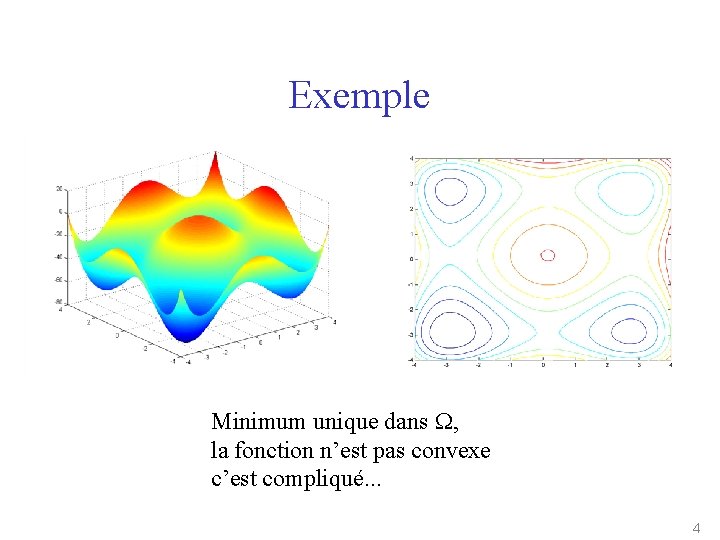
Exemple Minimum unique dans W, la fonction n’est pas convexe c’est compliqué. . . 4

Le cas des moindres carrés Problème de minimisation quadratique sans contraintes G symétrique définie positive : J est convexe il existe un minimum unique 5

Théorèmes d’existence Définition : soit J : Rn R, le point u est un minimum relatif de J, s’il existe un voisinage V de u tel que : Théorème : si J admet un est un minimum relatif en u, et si J est dérivable en ce point, Alors Remarque : on appelle parfois cette équation l’équation d’Euler du problème de minimisation Démonstration : 6

Théorème d’existence Définition : soit ji : Rn R, des fonctions continues. Soit u un point de l’ensemble en lequel les dérivées j’i(u) sont linéairement indépendantes. Théorème : si J admet un est un minimum relatif en u U, si J est dérivable en ce point et tel que ji(u)=0, i=1, m Alors il existe m nombres li définis de façon unique : Remarque : on appelle les li les multiplicateurs de Lagrange cette équation est celle « d’Euler-Lagrange » Démonstration : 7

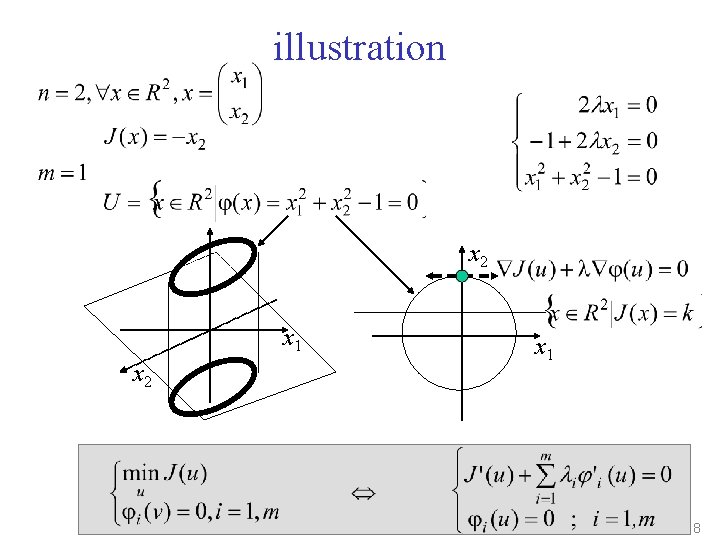
illustration x 2 x 1 8

Le cas des moindres carrés sous contraintes 1 n 1 m G CT a = h C 0 l d 9

Ça marche - ça ne marche pas La condition est nécessaire, et non suffisante il faut de la convexité ! 10

La convexité Ensemble convexe ensemble non convexe - fonction convexe fonction non convexe x y x y Définition : un sous ensemble K de Rn est dit convexe Définition : une fonction f : K Rn , avec K convexe est dite convexe Théorème : f est convexe ssi la matrice Hessiène de f est définie positive Théorème : soit f : K Rn , strictement convexe avec K convexe. Alors, le minimum de f sur K, s’il existe est unique. 11

Les algorithmes d’optimisation • Directes (ex : moindres carrés) • Itératives – Newton – Descente : Pas de descente Direction de descente 12