ASI 3 Mthodes numriques pour lingnieur la mthode



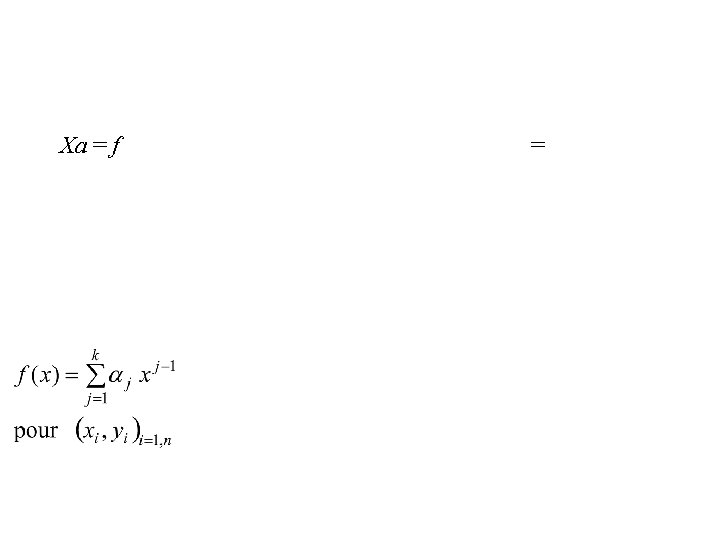
















- Slides: 26

ASI 3 Méthodes numériques pour l’ingénieur la méthode des moindres carrés Le point de vue numérique (factorisation QR)

Approximation/interpollation: moindres carrés f(x) yi xi

Posons le problème matriciellement
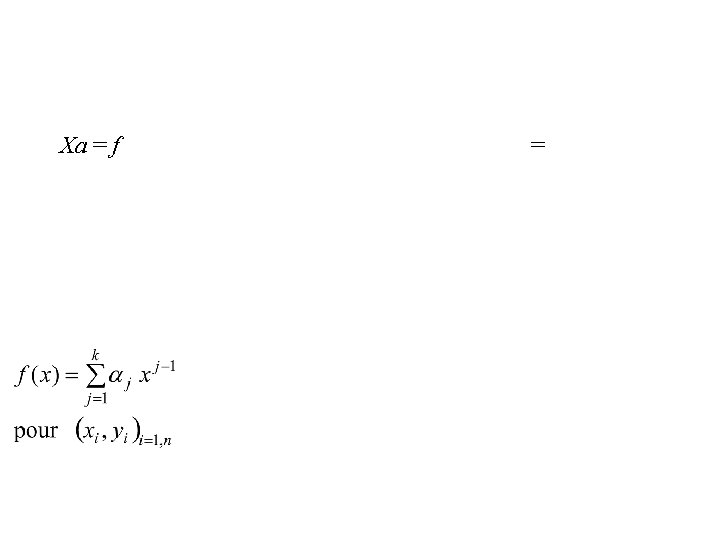
Xa = f Posons le problème matriciellement =

Approximation au sens des moindres carrés Système linéaire de k équations et k inconnues

Approximation : version matricielle Erreur d’approximation Système linéaire de k équations et k inconnues

Approximation : version Erreur d’approximation matricielle Matrice de Vandermonde (1735 -1796) Système linéaire de k équations et k inconnues

Forme quadratique Équations normales

Point de vue algèbrique (géométrique) X représente une application linéaire de Rp sur Rn Projection de y (les résultats des expériences) sur le sous espace vectoriel engendré par X (les données) y 0

Comment résoudre le problème des moindres carrées ? Rang(X’X) = Rang(X) = 3 cond(X’X) = cond(X)*cond(X) Il faut mieux travailler sur X que sur X’X … si possible !

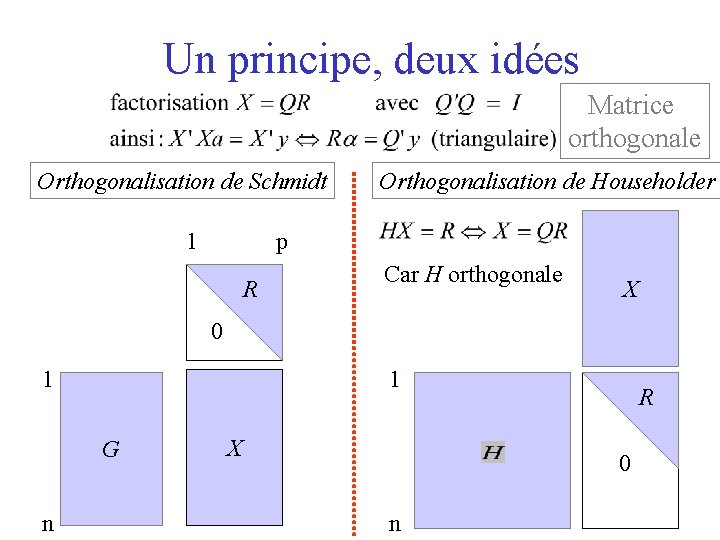
Un principe, deux idées Matrice orthogonale Orthogonalisation de Schmidt 1 Orthogonalisation de Householder p R Car H orthogonale X 0 1 1 G n X R H n 0

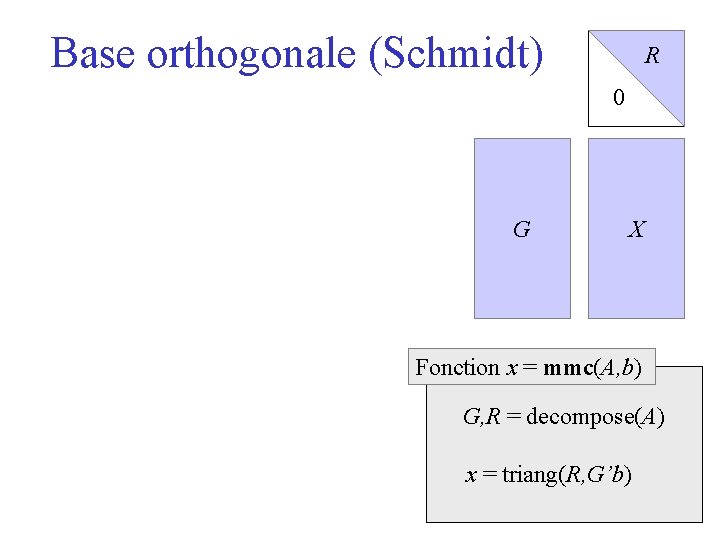
Base orthogonale (Schmidt) R 0 G X Fonction x = mmc(A, b) G, R = decompose(A) x = triang(R, G’b)

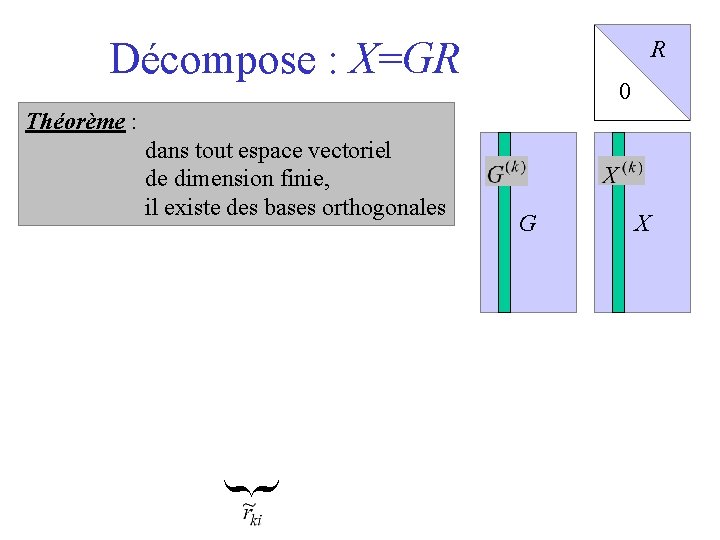
Décompose : X=GR R 0 Théorème : { dans tout espace vectoriel de dimension finie, il existe des bases orthogonales G X

Décompose : X=GR Fonction G, R = décompose(A) Problème d’accumulation d’erreurs d’arrondi

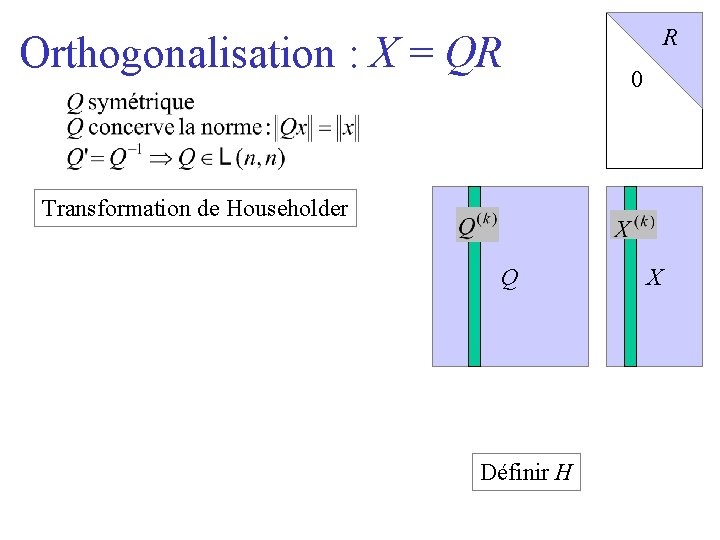
La méthode QR Il est si facile le résoudre un système « triangulaire » ! Q « facilement » inversible et R triangulaire Définition : on appelle matrice de Householder du vecteur normé u une matrice H de la forme suivante Propriété : une matrice de Householder est symétrique et orthogonale HTH=I Les transformations orthogonales « conservent » la norme

Orthogonalisation : X = QR R 0 Transformation de Householder Q Définir H X

Householder et moindres carrés

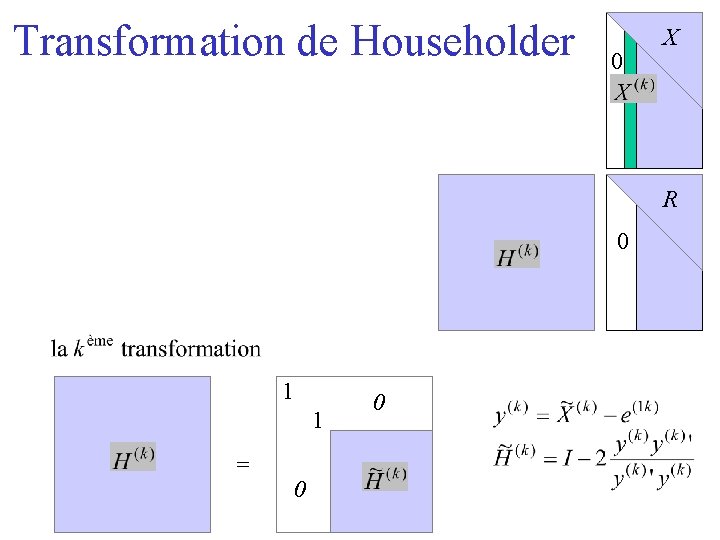
Transformation de Householder

Transformation de Householder Théorème : pour tout vecteur normé x, pour le vecteur unitaire e 1 il existe une matrice H telle que : Hx=e 1 Démonstration : posons

Transformation de Householder 0 X R H 1 1 H = 0 0 H 0

Quels calculs ?

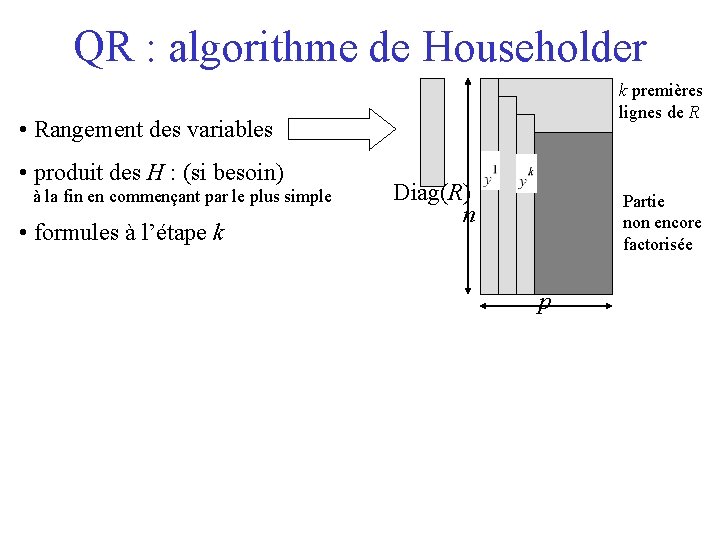
QR : algorithme de Householder k premières lignes de R • Rangement des variables • produit des H : (si besoin) à la fin en commençant par le plus simple • formules à l’étape k Diag(R) n Partie non encore factorisée p

L’algorithme QR Fonction Q, R = décompose. QR(X)

Retour des moindres carrées la méthode QR Mise en œuvre : on calcule directement Q’b pendant la décomposition

Remarques MMC sans Q R=chol(A’A) Si on ajoute ou on enlève une variable Q et R changent « peu »

Matlab ATTENTION : cette semaine il faut un compte rendu par binôme un. CR est une page recto verso : recto ce que vous avez fait, verso : ce que vous en pensez !