ASI 3 Mthodes numriques pour lingnieur Rsolution de

ASI 3 Méthodes numériques pour l’ingénieur Résolution de systèmes linéaires par des méthodes directes : LDL’ et Choleski

Résoudre un système linéaire Fonction x = Gauss(A, b) U, c = descent(A, b) x = triang(U, c) Fonction x = LU(A, b) L, U = decompose(A) y = triang(L, b) x = triang(U, y) Cas particulier : A est symétrique définie positive

Matrice à diagonale dominante Définition : une matrice carrée A est dite à diagonale dominante ssi : Théorème : Si A est a diagonale strictement dominante, Alors est elle alors non singulière, De plus Gauss est stable et peut fonctionner sans changement de colonne Éléments de démonstration : Ax=0, par l’absurde

Matrice symétrique définie positive Symétrique : A’=A Définie positive : Exemple : Rappelez vous des moindres carrés

Exemple

Exemple

Propriétés des matrices définies positives Théorème : Si A est une matrice n x n strictement définie positive Alors : – A est non singulière – aii > 0 pour i=1, n

Propriétés des matrices définies positives Théorème : Si A est une matrice n x n strictement définie positive Alors : – A est non singulière – aii > 0 pour i=1, n

Propriétés des matrices définies positives Théorème : Si A est une matrice n x n symétrique strictement définie positive Alors :

Propriétés des matrices définies positives Théorème : Si A est une matrice n x n symétrique strictement définie positive Alors :

Autres propriétés Définition : une sous matrice principale d’une matrice A est une matrice carrée de la forme A(1: i, 1: i) quelque soit i Théorème : Une matrice symétrique est définie positive ssi chacune de ses sous matrice principales à un déterminant positif

Autres propriétés Définition : une sous matrice principale d’une matrice A est une matrice carrée de la forme A(1: i, 1: i) quelque soit i Théorème : Une matrice symétrique est définie positive ssi chacune de ses sous matrice principales à un déterminant positif

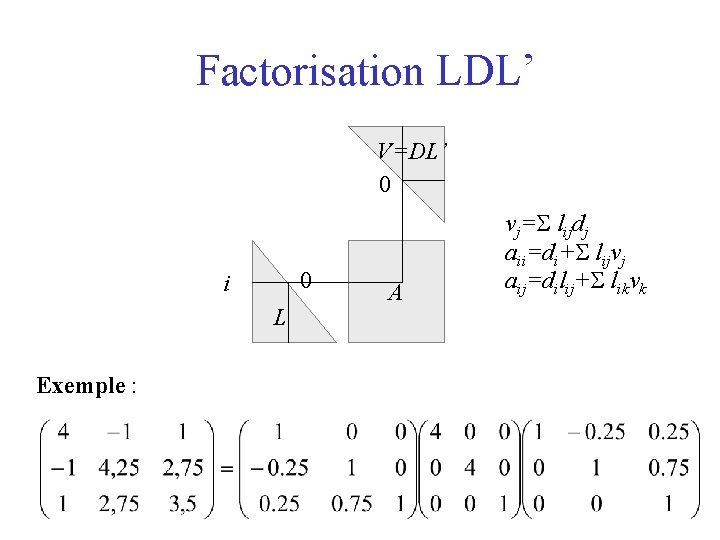
Autres propriétés Théorème : Une matrice est symétrique définie positive si la méthode de Gauss être appliquée sans permutations n’admet que des pivots positifs De plus, le résultat est stable par rapport aux erreurs d’arrondi Corollaire si A est une matrice symétrique non singulière, Alors il existe une matrice diagonale D et une matrice triangulaire avec des 1 sur la diagonale L telles que : A = LDL’ éléments de démonstration : A non singulière => A=LU =LDV et A’=V’DL’ que l’on identifie car A est symétrique

Factorisation LDL’ V=DL’ 0 0 i L Exemple : A vj=S lijdj aii=di+S lijvj aij=dilij+S likvk

La factorisation LDL’ Fonction L, D = décompose. LDL(A)

Choleski : LL’ D doit être positif ! Théorème : toute matrice A symétrique définie positive admet une décomposition unique sous la forme A=LL’ ou L est une matrice triangulaire inférieure dont tous les éléments diagonaux sont positifs

Choleski : l’algorithme Fonction L = Choleski(A)

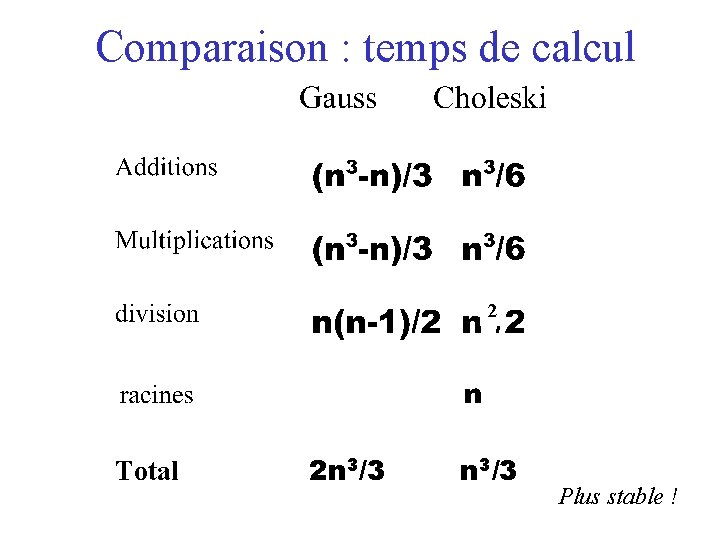
Comparaison : temps de calcul 2 Total 2 n 3/3 Plus stable !

Logiciels – Cas général : PA=LU – Matrice symétrique définie positive : A=LL’ (Choleski) – Matrice symétrique : A=LDL’ – Matrice tridiagonale (heisenberg) : LU par bande (cf TD) – Matrice triangulaire : « remontée en n 2 » Matlab : x =Ab ; si A triangulaire : x=trisup(A, b) sinon si A symétrique définie positive ; L=chol(A) sinon : (* cas général*) [L, U, P]=lu(A); z=L(P*b); x=Uz; LAPACK = BLAS (basic linear algebra subprograms) - blaise, octave, matlab (interprétés calcul) - scilab, maple (interprétés formels) - IMSL, NAG (bibliothèques)