ASI 3 Mthodes numriques pour lingnieur Introduction vecteurs

















- Slides: 17

ASI 3 Méthodes numériques pour l’ingénieur Introduction : vecteurs, matrices et applications linéaires

Opérations sur les vecteurs Vecteur x base (canonique) bi , i=1, n espace vectoriel V sur le corps des réels combinaison linéaire sous espace vectoriel base, dimension

Opérations sur les vecteurs Somme multiplication ? Vecteur transposé Norme produit scalaire, vecteurs orthogonaux

Normes et produit scalaire

Matrices Tableau de n lignes et k colonnes Remarque fondamentale : on ne peut rien démontrer sans faire référence à l’application linéaire que la matrice représente

Applications linéaires Définition : Propriétés : Soient E et F deux espaces vectoriels Noyau : image : Noyau et image sont des s. e. v. resp. de E et de F image : s. e. v engendré par u(ei) rang = dim(Im(u)) u injective (ker(u) = 0) u surjective Im(u) = F Par identification, on donne une signification aux colonnes de la matrice

Applications linéaires et matrices

Propriétés des matrices u, A Img(A) • 0 Ker(A) Rk Rn

Propriété des matrices – Soit A une matrice associée à une application linéaire u de E dans F – soit k = dim(E) et n=dim(F) Noyau Rang (nombre de colonnes linéairement indépendantes) variables équivalentes équations équivalentes systèmes liés - systèmes libres (matrices blocs) vecteurs propres

Opérations sur les matrices Somme : somme des applications linéaires produit : composition des applications linéaires n A AB n’est pas BA (non commutatif) B n q p

Complexité algorithmique Quel est l’algorithme qui calcule C=AB le plus vite ? Définitions – grand O – petit o – équivalence asymptotique A, B et C sont des matrices carrées de taille n O(n 2) < Algorithme < O(n 3) Exemple, n=2 23 = 8 multiplications Comme Strassen, 1969 sauriez vous faire mieux ?

Complexité algorithmique Quel est l’algorithme qui calcule C=AB le plus vite ? Exemple, n=2 Strassen, 1969 o(n 2) < Algorithme < O(nlog 27) 2, 807 log 10(n) 1 2 3 4 5 6 7 8 9 10 n 3/n(log 2(7)) 1. 5 2. 4 3. 7 5. 8 9. 1 14. 3 22. 3 34. 7 54. 1 84. 4

Opérations sur les matrices Inverse (a. l. bijective <=> matrice carrée) matrice identité I Transposée (adjointe pour les complexes) A est symétrique ssi A’=A Permutation p associé à la matrice P (changement de base de ei à ep(i))

Opérations sur les matrices Changement de base déterminant d’une matrice carrée

Quelques matrices particulières Matrices carrées Matrices diagonales Matrices triangulaires (inférieure et supérieure) Matrices par bandes Matrice diagonale (strictement) dominante Matrice symétrique Matrice de Vandermonde (déjà vu en introduction) Matrice de Toeplitz Matrice de Hankel

4 principes fondamentaux On ne change pas la solution lorsque l’on : 1. permute 2 lignes interprétation physique 2. permute 2 colonnes 3. divise par un même terme non nul les éléments d’une ligne 4. ajoute ou retranche à une ligne un certain nombre de fois une autre ligne

Question fondamentale A quelles conditions l’équation Ax = b admet-elle une solution unique ? Théorème Dim(Im u)+dim(ker u) = dim(F) rang(u)+dim(ker u) = dim(F) corollaire
 Figure changement de base
Figure changement de base Calcul vecteur
Calcul vecteur Vecteur et translation
Vecteur et translation Vecteurs et translations
Vecteurs et translations Les vecteurs de clonage
Les vecteurs de clonage Vecteurs de clonage
Vecteurs de clonage Coop pour toi et pour moi
Coop pour toi et pour moi Organisateur textuel pour commencer un texte
Organisateur textuel pour commencer un texte Asi esp promotional products
Asi esp promotional products Hermano así
Hermano así Tanto tiempo disfrutamos este amor
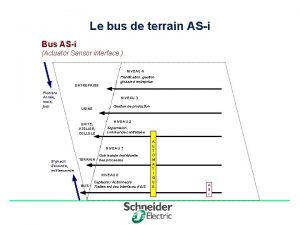
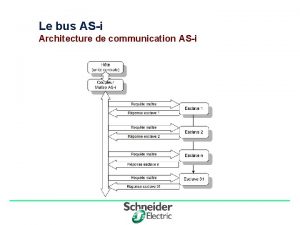
Tanto tiempo disfrutamos este amor Asi bus
Asi bus Te quiero gordita
Te quiero gordita Konstruē funkcijas grafiku
Konstruē funkcijas grafiku Aktif ve pasif bağışıklık örnekleri
Aktif ve pasif bağışıklık örnekleri Los conectores de contraste
Los conectores de contraste Barbara negri
Barbara negri Sieć asi
Sieć asi