Chapitre 8 Vecteurs et translations I Les vecteurs

Chapitre 8 Vecteurs et translations I. Les vecteurs et les translations : 1. Les vecteurs : 2. La translation : II. Composée de deux translations et somme de deux vecteurs : 1. Introduction et définition : 2. Construction de la somme de deux vecteurs : a. Cas où les vecteurs se suivent : b. Cas où les vecteurs partent du même point : c. Cas général : III. Composée de deux symétries centrales :

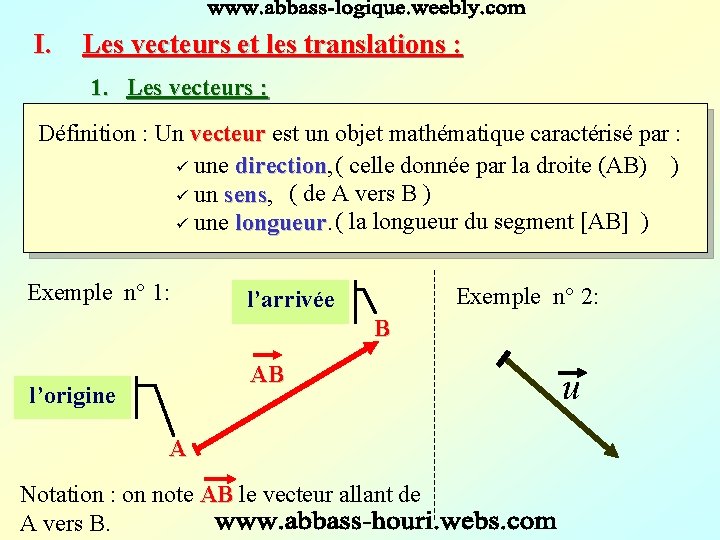
I. Les vecteurs et les translations : 1. Les vecteurs : Définition : Un vecteur est un objet mathématique caractérisé par : vecteur ü une direction, direction ( celle donnée par la droite (AB) ) ü un sens, sens ( de A vers B ) ü une longueur ( la longueur du segment [AB] ) Exemple n° 1: Exemple n° 2: l’arrivée B AB l’origine A Notation : on note AB le vecteur allant de AB A vers B. u

Remarques : ü la longueur du vecteur AB s’appelle également la norme du vecteur AB la norme et se note || AB ||. ü un vecteur n’est pas fixe. Quelques vecteurs particuliers : • Soit A un point quelconque, AA est appelé le vecteur nul et AA est noté O AA ou O • Le vecteur BA est l’opposé du vecteur AB et on note BA = − AB BA l’opposé AB A AB BA ou − AB B Deux vecteurs opposés ont : ü la même direction, ü la même longueur, ü des sens contraires

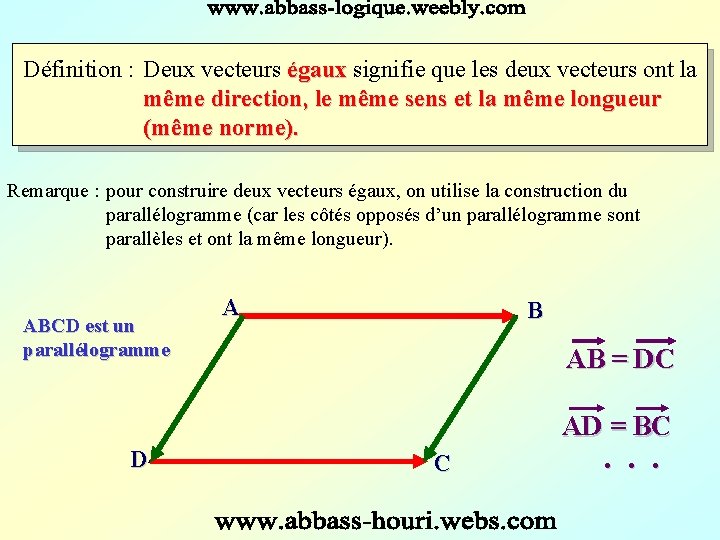
Définition : Deux vecteurs égaux signifie que les deux vecteurs ont la égaux même direction, le même sens et la même longueur (même norme). Remarque : pour construire deux vecteurs égaux, on utilise la construction du parallélogramme (car les côtés opposés d’un parallélogramme sont parallèles et ont la même longueur). ABCD est un parallélogramme A B AB = DC AD = BC D C . . .

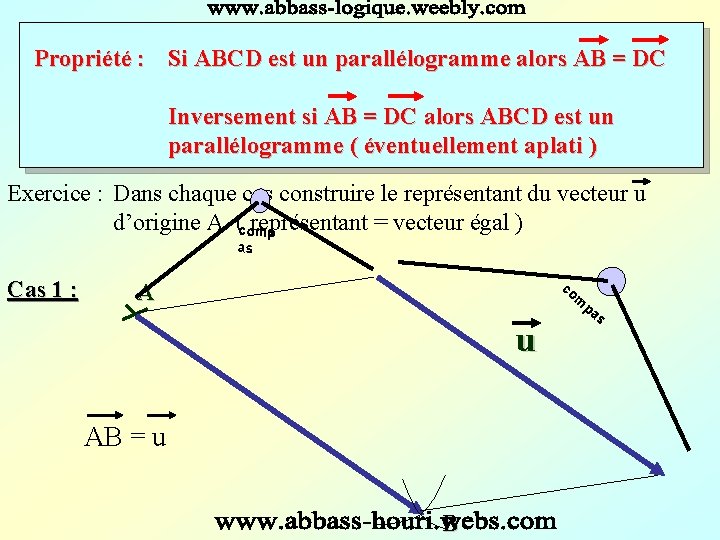
Propriété : Si ABCD est un parallélogramme alors AB = DC Inversement si AB = DC alors ABCD est un parallélogramme ( éventuellement aplati ) Exercice : Dans chaque cas construire le représentant du vecteur u d’origine A ( représentant = vecteur égal ) comp as Cas 1 : co m A u AB = u B pa s

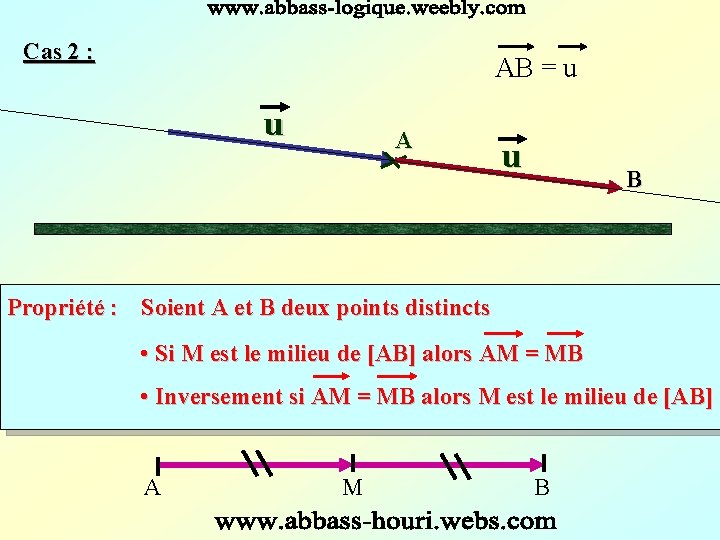
Cas 2 : AB = u u A u B Propriété : Soient A et B deux points distincts • Si M est le milieu de [AB] alors AM = MB • Inversement si AM = MB alors M est le milieu de [AB] A M B

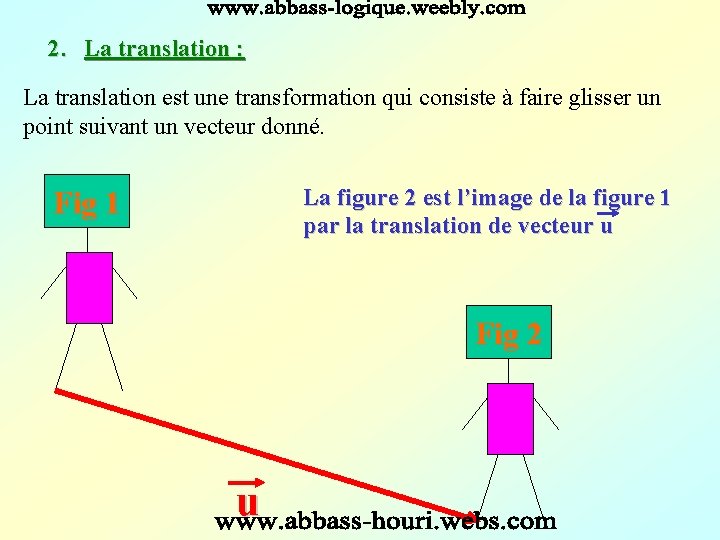
2. La translation : La translation est une transformation qui consiste à faire glisser un point suivant un vecteur donné. La figure 2 est l’image de la figure 1 par la translation de vecteur u Fig 1 Fig 2 u

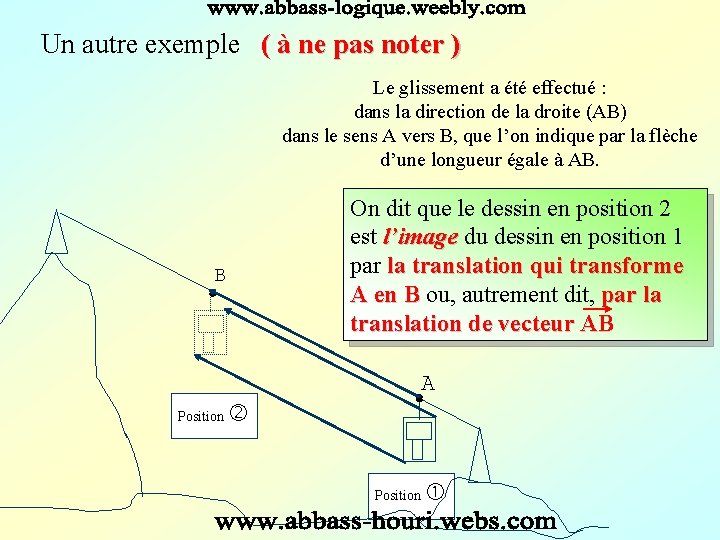
Un autre exemple ( à ne pas noter ) Le glissement a été effectué : dans la direction de la droite (AB) dans le sens A vers B, que l’on indique par la flèche d’une longueur égale à AB. On dit que le dessin en position 2 est l’image du dessin en position 1 l’image par la translation qui transforme A en B ou, autrement dit, par la A en B translation de vecteur AB B A Position

Définition : Soit M un point et AB un vecteur, On dit que M’ est l’image de M par la translation de vecteur AB lorsque MM’ = AB vecteur AB On note : M’ = tu( M ) tu : translation de vecteur u

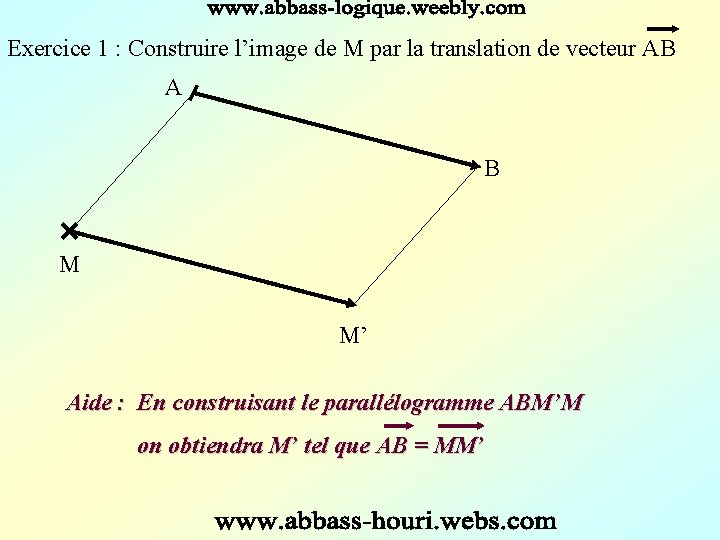
Exercice 1 : Construire l’image de M par la translation de vecteur AB A B M M’ Aide : En construisant le parallélogramme ABM’M on obtiendra M’ tel que AB = MM’

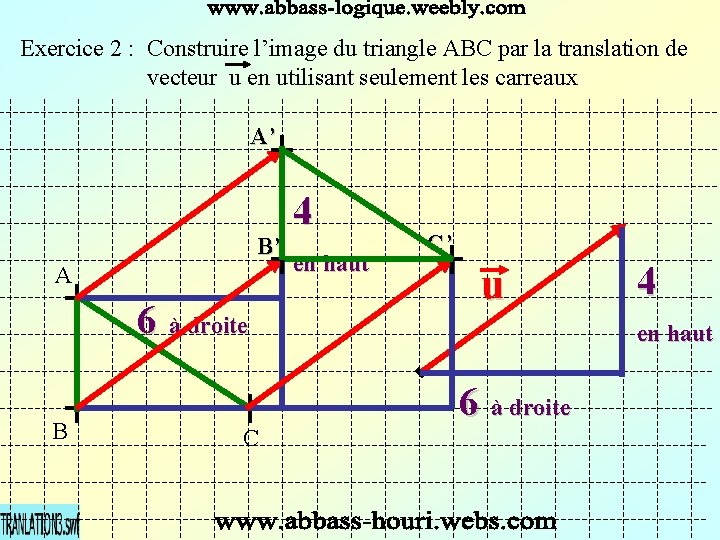
Exercice 2 : Construire l’image du triangle ABC par la translation de vecteur u en utilisant seulement les carreaux A’ B’ A 6 à droite B C 4 en haut C’ u 4 en haut 6 à droite

Propriétés : La translation transforme une figure en une figure superposable. La translation conserve : • les distances, • l’alignement des points, • le parallélisme ou l’orthogonalité des droites, • les mesures des angles, • les milieux des segments, • les aires et les périmètres.

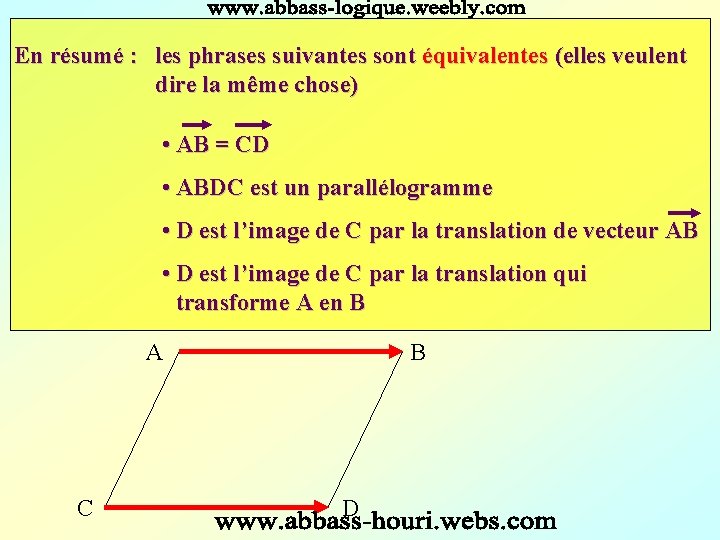
En résumé : les phrases suivantes sont équivalentes (elles veulent dire la même chose) • AB = CD • ABDC est un parallélogramme • D est l’image de C par la translation de vecteur AB • D est l’image de C par la translation qui transforme A en B A C B D

II. Composée de deux translations et somme de deux vecteurs : 1. Introduction et définition : Construisons l’image de F 1 par la translation de vecteur AB. On note F 2 F 1 B Construisons l’image de F 2 par la translation de vecteur BC. On note F 3 A C Conclusion : Il existe une translation permettant de passer directement de F 1 à F 3. C’est la translation de vecteur AC.

Propriété : A, B et C étant trois points du plan, la composée de la composée translation de vecteur AB suivie de la translation de vecteur BC est la translation de vecteur AC. On dit que le vecteur AC est la somme des vecteurs AB la somme et BC On note AC = AB + BC ( cette relation est appelée « relation de Chasles » ) « relation de Chasles »

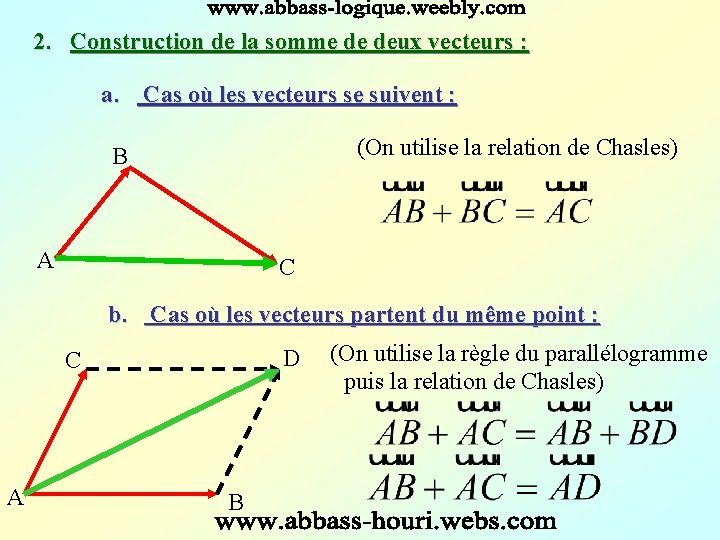
2. Construction de la somme de deux vecteurs : a. Cas où les vecteurs se suivent : (On utilise la relation de Chasles) B A C b. Cas où les vecteurs partent du même point : D C A B (On utilise la règle du parallélogramme puis la relation de Chasles)

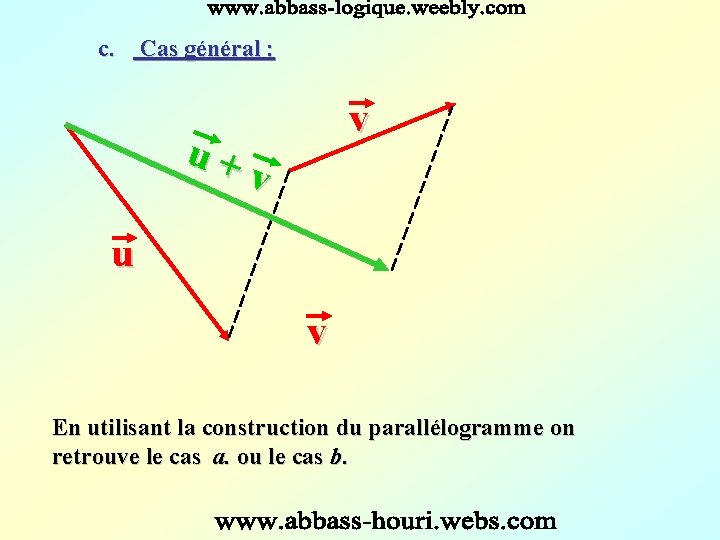
c. Cas général : v u + v u v En utilisant la construction du parallélogramme on retrouve le cas a. ou le cas b.

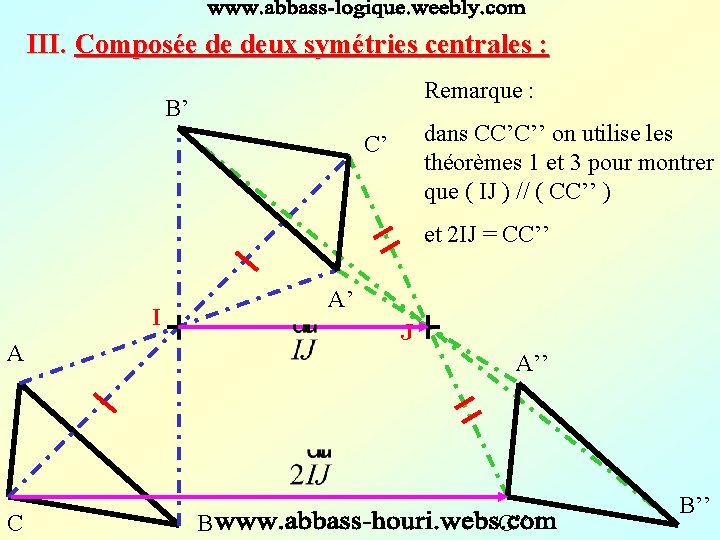
III. Composée de deux symétries centrales : Remarque : B’ dans CC’C’’ on utilise les théorèmes 1 et 3 pour montrer que ( IJ ) // ( CC’’ ) C’ et 2 IJ = CC’’ A’ I J A C A’’ B C’’ B’’

Propriété : I et J étant deux points du plan, la composée de la symétrie de centre I suivie de la symétrie de centre J est la translation de vecteur IJ + IJ que l’on note 2 IJ Quelques notations : M’ = tu( M ) signifie que M’ est l’image de M par la translation de vecteur u M’ = s. A( M ) signifie que M’ est l’image de M par la symétrie de centre A M’ = s(d)( M ) signifie que M’ est l’image de M par la symétrie d’axe (d)