Analysis of Variance ANOVA Analysis of Variance ANOVA

























- Slides: 32

Analysis of Variance (ANOVA)

Analysis of Variance (ANOVA) n Hypothesis H 0 : mi = m. G H 1 : i | ( mi m. G ) n Logic S 2 within = error variability S 2 between = error variability + treatment Where, x = grand mean, xj = group mean, k = number of groups, nj = number of participants in a group, N = Total number of participants

Classic ANOVA Table Total variability = Between variability + within variability Sums of square

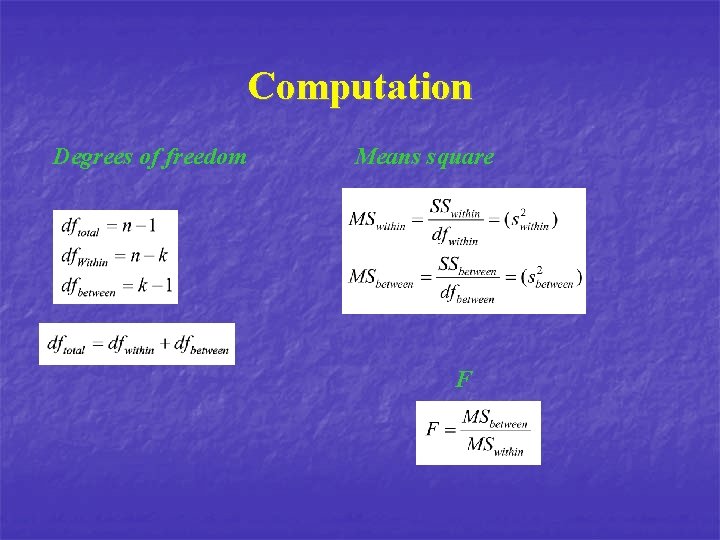
Computation Degrees of freedom Means square F

ANOVA

Analysis of Variance (ANOVA) n If the independent variables are continuous and the dependant variable is also continuous then we will perform a multiple regression. Now, if the independent variables are discrete and the dependant variable is still continuous we will performed an ANOVA where, m = grand mean, t = treatment effect, e = error From ANOVA To GLM where,

Analysis of Variance (ANOVA) n Example

Analysis of Variance (ANOVA) Using the GLM approach through a coding matrix n Logic: n If, for example, there are 3 groups and we know that the participant number 12 is not part of the first nor the second group, then we know that this participant is necessary part of group 3.

Analysis of Variance (ANOVA) Performing ANOVA using GLM through a coding matrix n Logic: n In other words, there is only 2 degrees of freedom in group assignation. Therefore, the third group column will be eliminated. n A value of 1 will be assigned to the participants of group i and a value of 0 for the other groups. Whereas, the last group will receive a value of -1 for all the group (balance things).

Analysis of Variance (ANOVA) Then, for each subject we associate its corresponding group coding. = independent variables (X)

Analysis of Variance (ANOVA) X y A= SSCP =

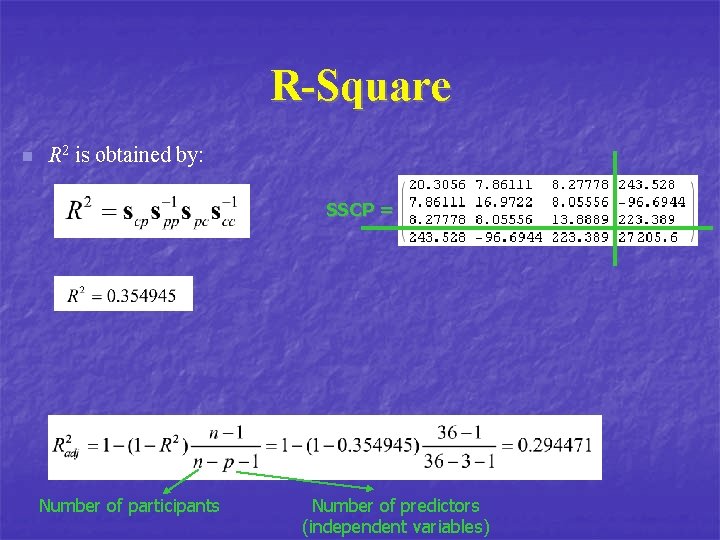
R-Square n R 2 is obtained by: SSCP = Number of participants Number of predictors (independent variables)

ANOVA Table n The hypothesis is that the R-Square between the predictors and the criterion is null. Since F(3, 32)=5. 86938, p<0. 05, we reject H 0 and we accept H 1. There is at least one group that is different from the others.

ANOVA Terminology n Coefficient of determination (proportion of explained variation)

ANOVA n Now you know it! n n ANOVA is a special case of regression. The same logic can be applied to t-test, factorial ANOVA, ANCOVA, simple effects (Tukey, Bonferoni, LSD, etc. )

Principal Component Analysis (PCA)

PCA n Why n n n To discover or to reduce the dimensionality of the data set. To identify new meaningful underlying variables Assumptions n n Sample size : about 300 (in general) Normality Linearity Absence of outliers among cases

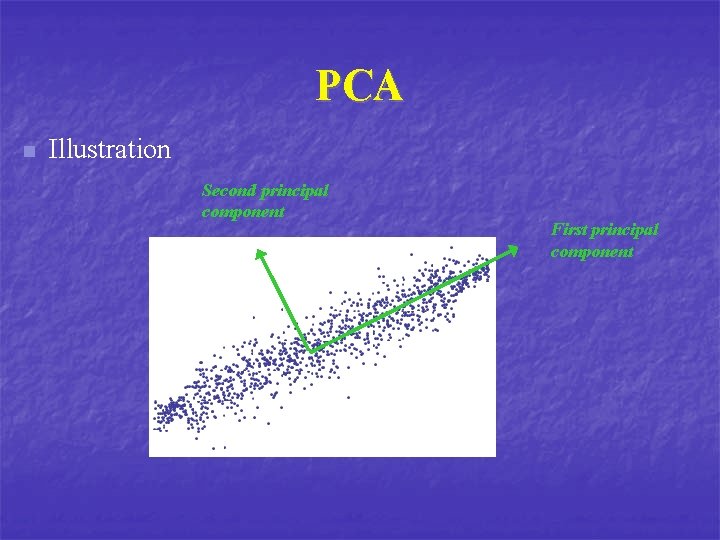
PCA n Illustration Second principal component First principal component

PCA n Preliminary n Data X= n Z scores Zx =

PCA n Preliminary n SSCP = n Correlation Matrix M=

PCA n Eigenvalues and eigenvectors n Let’s define a random vector as v(0) = [1, 1]T. Now, if we compute the inner product between the correlation matrix (M) and V(0) an re-multiply the result by M, again, and again, what the results will be after k iterations?

PCA n Eigenvalues and eigenvectors n Let’s define a random vector as v(0) = [1, 1]T. Now, if we compute the inner product between the correlation matrix (M) and V(0) an re-multiply the result by M, again, and again, what the results will be after k iterations?

PCA n Eigenvalues and eigenvectors n After convergence n n 1 - The direction of the stable vector = Eigenvector ( ) 2 - The stable vector lengthening factor = Eigenvalue ( )

PCA n Eigenvalues and eigenvectors n Once the first eigenvector (and associated eigenvalue) has been identified, we remove it from the matrix. n And we repeat the process until all the eigenvectors and eigenvalues have been extracted.

PCA n Eigenvalues and eigenvectors n n There will be as many eigenvectors/eigenvalues as there are variables. Each eigenvector will be orthogonal to the others. M= PCA

PCA n Eigenvalues and eigenvectors n n There will be as many eigenvectors/eigenvalues as there are variables. Each eigenvector will be orthogonal to the others. 1 2 3 4

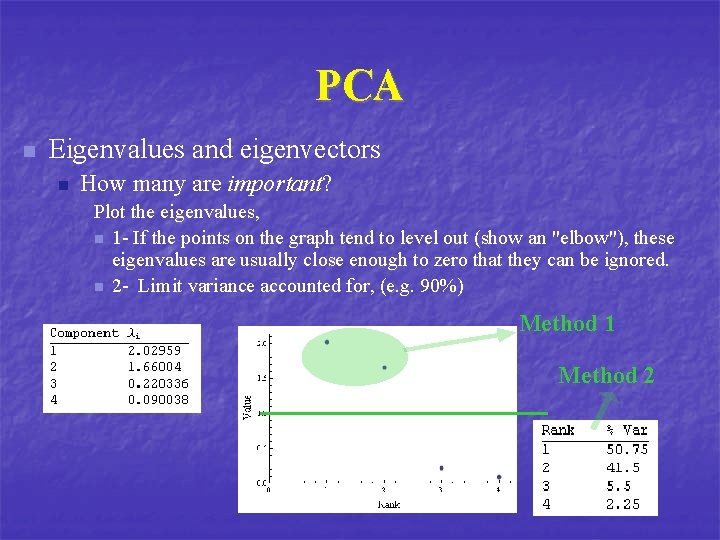
PCA n Eigenvalues and eigenvectors n How many are important? Plot the eigenvalues, n 1 - If the points on the graph tend to level out (show an "elbow"), these eigenvalues are usually close enough to zero that they can be ignored. n 2 - Limit variance accounted for, (e. g. 90%) Method 1 Method 2

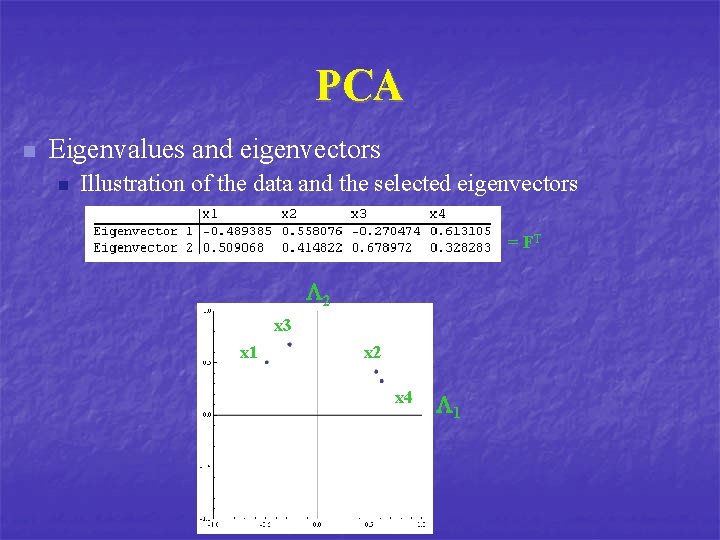
PCA n Eigenvalues and eigenvectors n Illustration of the data and the selected eigenvectors = FT 2 x 3 x 1 x 2 x 4 1

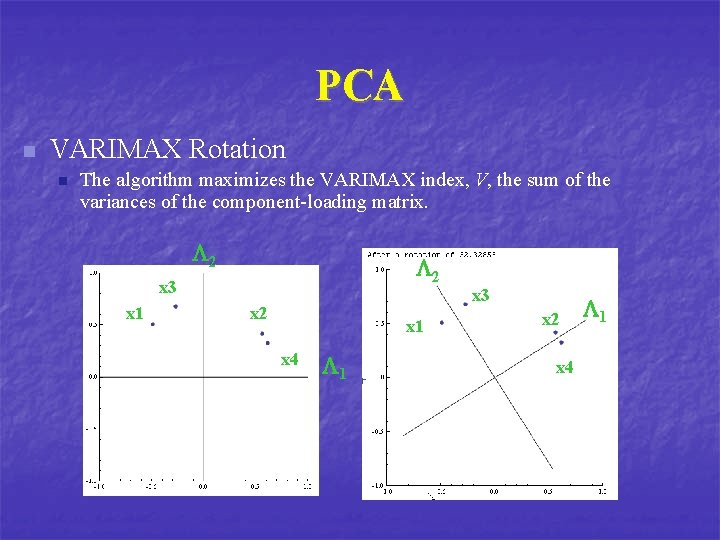
PCA n VARIMAX Rotation n n Why ? To improve the readability The VARIMAX rotation aims at finding a solution where an original variable loads highly on one particular factor and loads as low as possible on other factors. Rotation matrix

PCA n VARIMAX Rotation n The algorithm maximizes the VARIMAX index, V, the sum of the variances of the component-loading matrix. (X-X)2 n V will be a long equation that contains the q variable. An optimization technique is then used to find the value q that maximize V.

PCA n VARIMAX Rotation n The algorithm maximizes the VARIMAX index, V, the sum of the variances of the component-loading matrix. U= V=

PCA n VARIMAX Rotation n The algorithm maximizes the VARIMAX index, V, the sum of the variances of the component-loading matrix. 2 2 x 3 x 1 x 2 x 1 x 4 1 x 3 x 2 x 4 1
 Analysis of variance (anova)
Analysis of variance (anova) Perbedaan anova one way dan two way
Perbedaan anova one way dan two way One way anova vs two way anova
One way anova vs two way anova Contoh soal anova two way
Contoh soal anova two way Time variance
Time variance What is a static budget
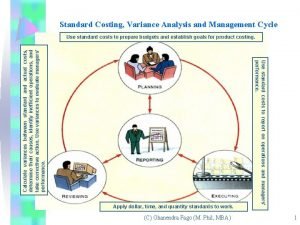
What is a static budget The variance analysis cycle:
The variance analysis cycle: Tr
Tr Standard costing formula
Standard costing formula Analysis of variance
Analysis of variance Direct materials variance
Direct materials variance Multivariate analysis of variance and covariance
Multivariate analysis of variance and covariance Material price variance
Material price variance Variance analysis definition
Variance analysis definition Spss mixed model
Spss mixed model Variance analysis in nursing
Variance analysis in nursing Budget variance example
Budget variance example Introduction to analysis of variance
Introduction to analysis of variance Analysis of variance and covariance
Analysis of variance and covariance Kaizen costing
Kaizen costing Cima variance analysis
Cima variance analysis When setting direct labor standards
When setting direct labor standards Variance analysis
Variance analysis Minitab 17
Minitab 17 Faktöriyel anova
Faktöriyel anova Sphärizitätsannahme
Sphärizitätsannahme Zweifaktorielle anova
Zweifaktorielle anova 2 factor anova table
2 factor anova table Two way anova
Two way anova 2 yönlü anova
2 yönlü anova Application of anova
Application of anova Analisis ragam anova
Analisis ragam anova One way anova table
One way anova table