OneWay ANOVA ANOVA Analysis of Variance This is


























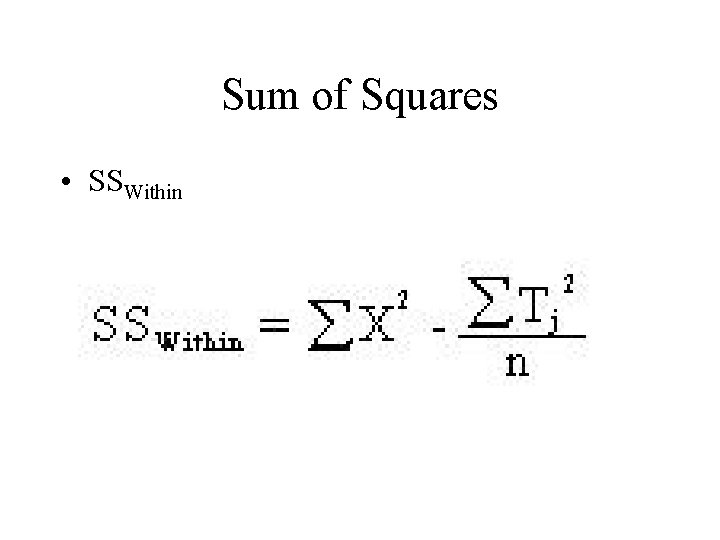




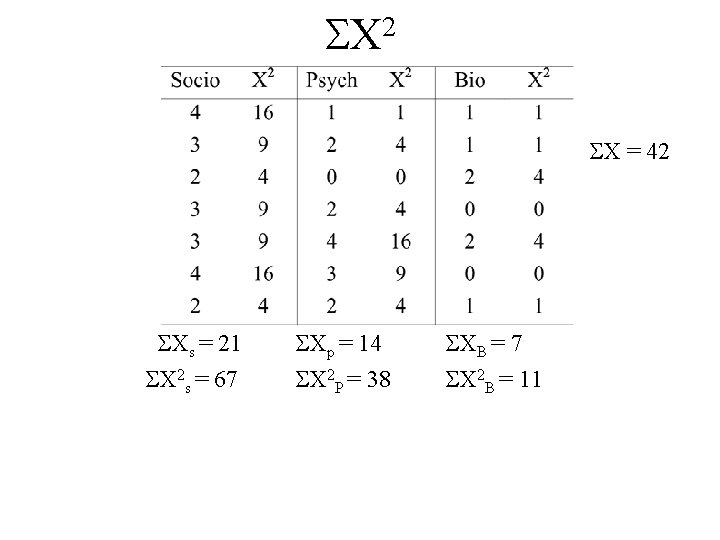
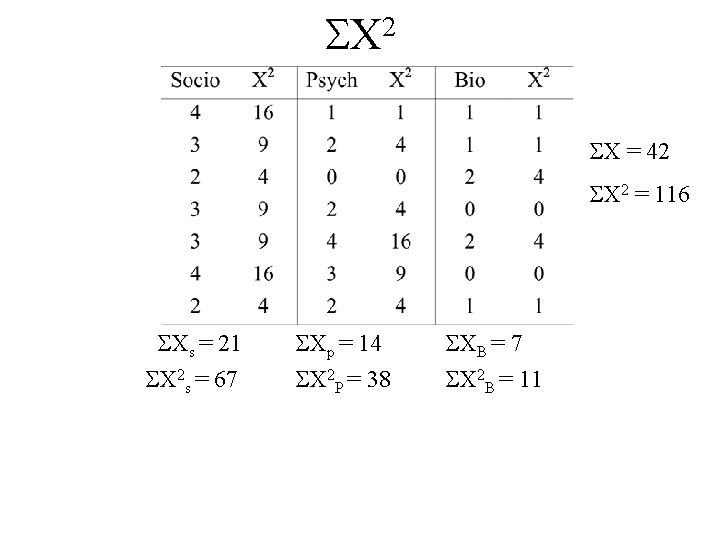
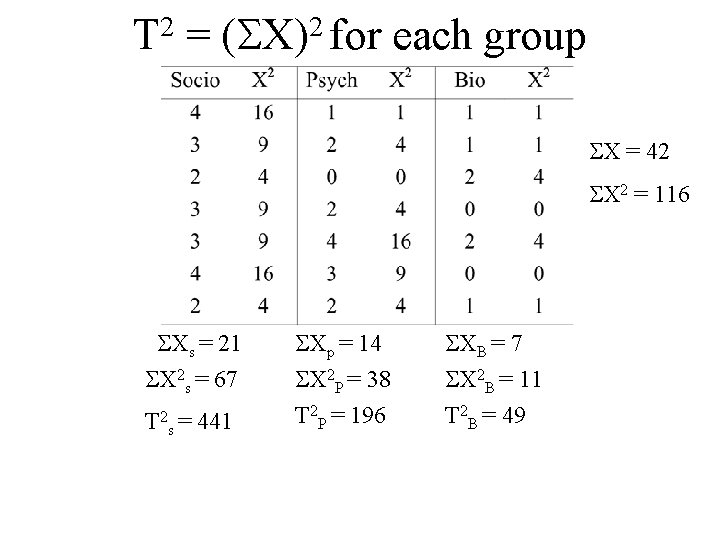
























- Slides: 64


One-Way ANOVA • ANOVA = Analysis of Variance • This is a technique used to analyze the results of an experiment when you have more than two groups

Example • You measure the number of days 7 psychology majors, 7 sociology majors, and 7 biology majors are absent from class • You wonder if the average number of days each of these three groups was absent is significantly different from one another

Results X = 3. 00 X = 2. 00 X = 1. 00

Hypothesis • Alternative hypothesis (H 1) • H 1: The three population means are not all equal

Hypothesis • Null hypothesis (H 0) psych = socio = bio

Between and Within Group Variability • Two types of variability • Between – the differences between the mean scores of the three groups – The more different these means are, the more variability!

Results X = 3. 00 X = 2. 00 X = 1. 00

Between Variability S 2 =. 66 X = 3. 00 X = 2. 00 X = 1. 00

Between Group Variability • What causes this variability to increase? • 1) Effect of the variable (college major) • 2) Sampling error

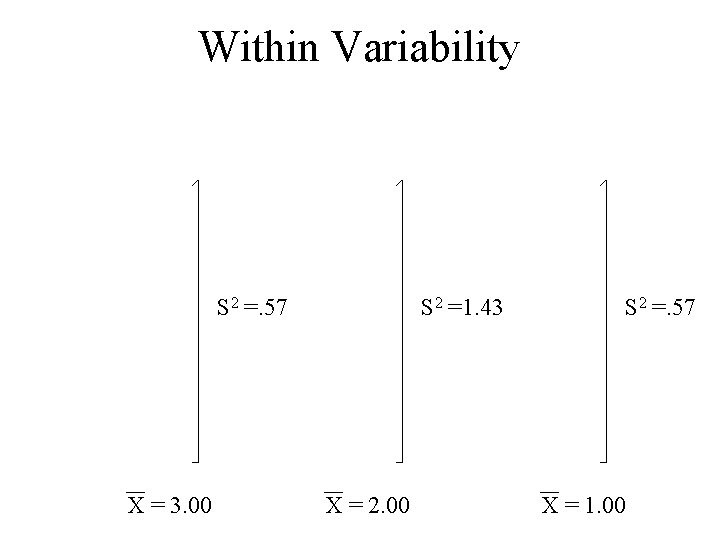
Between and Within Group Variability • Two types of variability • Within – the variability of the scores within each group

Results X = 3. 00 X = 2. 00 X = 1. 00

Within Variability S 2 =. 57 X = 3. 00 S 2 =1. 43 X = 2. 00 S 2 =. 57 X = 1. 00

Within Group Variability • What causes this variability to increase? • 1) Sampling error

Between and Within Group Variability Between-group variability Within-group variability

Between and Within Group Variability sampling error + effect of variable sampling error

Between and Within Group Variability sampling error + effect of variable sampling error Thus, if null hypothesis was true this would result in a value of 1. 00

Between and Within Group Variability sampling error + effect of variable sampling error Thus, if null hypothesis was not true this value would be greater than 1. 00


Calculating this Variance Ratio

Calculating this Variance Ratio

Calculating this Variance Ratio

Degrees of Freedom • dfbetween • dfwithin • dftotal = dfbetween + dfwithin

Degrees of Freedom • dfbetween = k - 1 • dfwithin = N - k • dftotal = N - 1 (k = number of groups) (N = total number of observations) • dftotal = dfbetween + dfwithin

Degrees of Freedom • dfbetween = k - 1 • dfwithin = N - k • dftotal = N - 1 • 20 = 2 + 18 3 -1=2 21 - 3 = 18 21 - 1 = 20

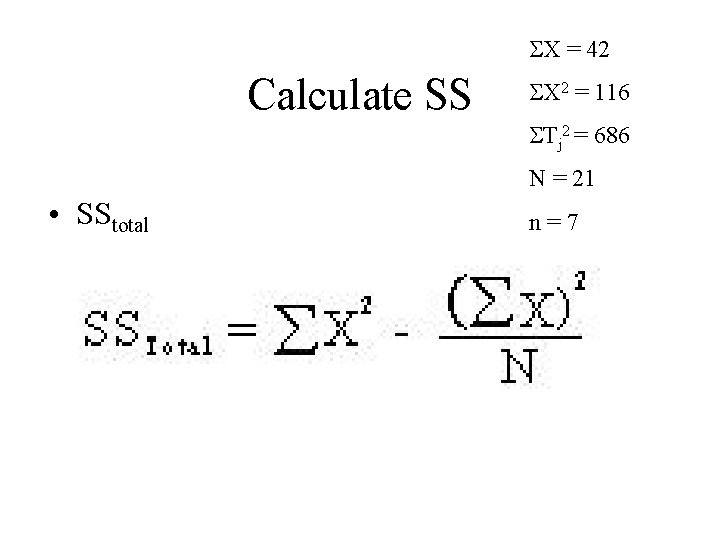
Sum of Squares • SSBetween • SSWithin • SStotal = SSBetween + SSWithin

Sum of Squares • SStotal
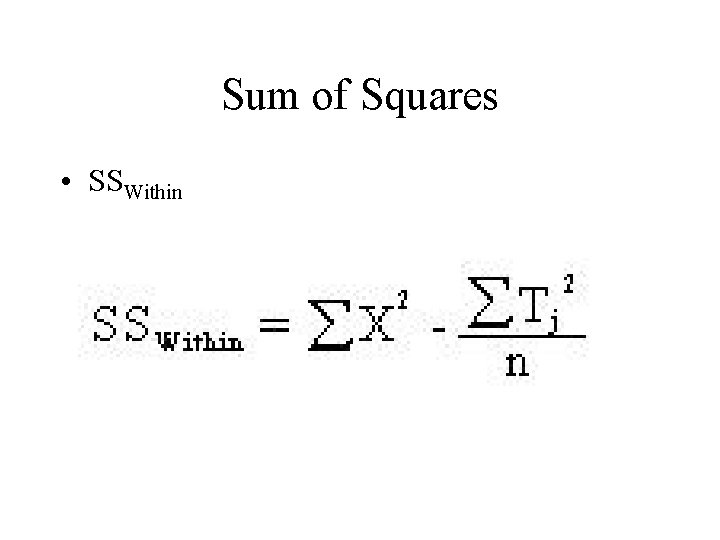
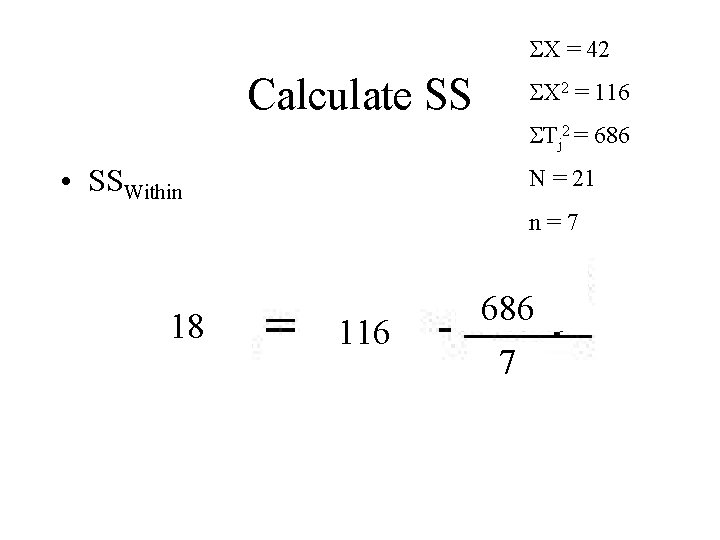
Sum of Squares • SSWithin

Sum of Squares • SSBetween

Sum of Squares • Ingredients: • • • X X 2 Tj 2 N n

To Calculate the SS

X Xs = 21 Xp = 14 XB = 7

X X = 42 Xs = 21 Xp = 14 XB = 7
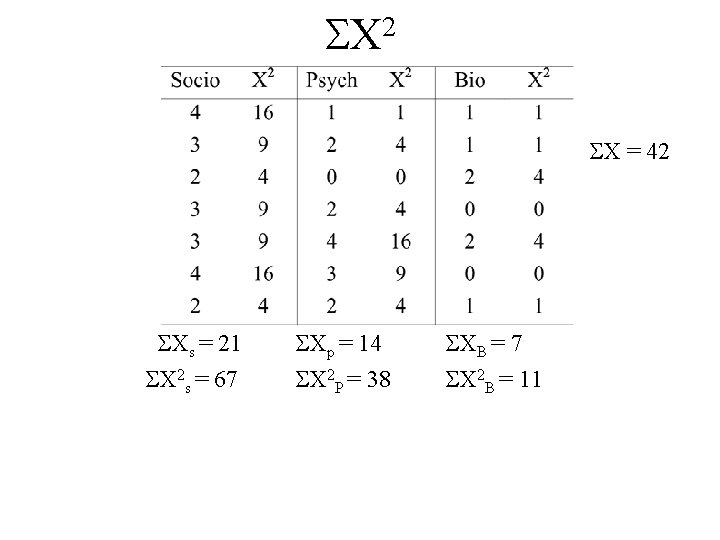
2 X X = 42 Xs = 21 X 2 s = 67 Xp = 14 X 2 P = 38 XB = 7 X 2 B = 11
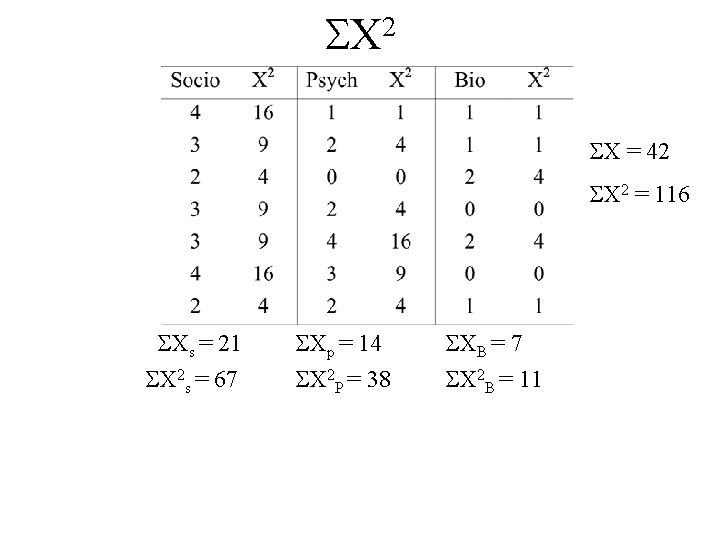
2 X X = 42 X 2 = 116 Xs = 21 X 2 s = 67 Xp = 14 X 2 P = 38 XB = 7 X 2 B = 11
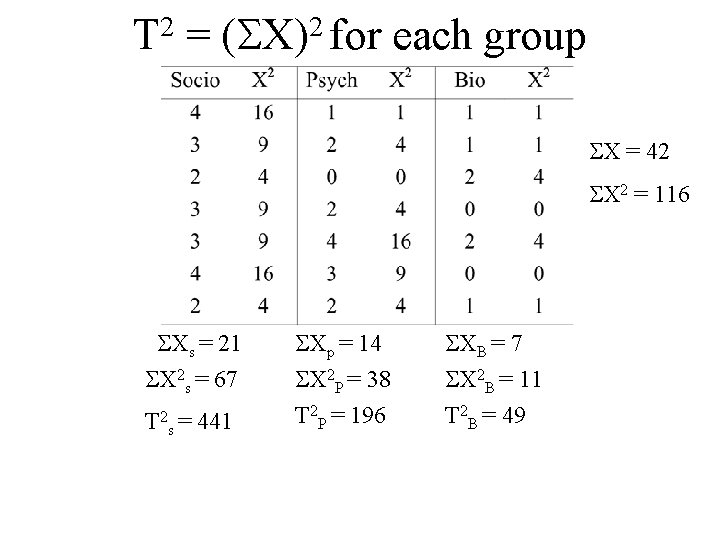
2 T = 2 ( X) for each group X = 42 X 2 = 116 Xs = 21 X 2 s = 67 T 2 s = 441 Xp = 14 X 2 P = 38 T 2 P = 196 XB = 7 X 2 B = 11 T 2 B = 49

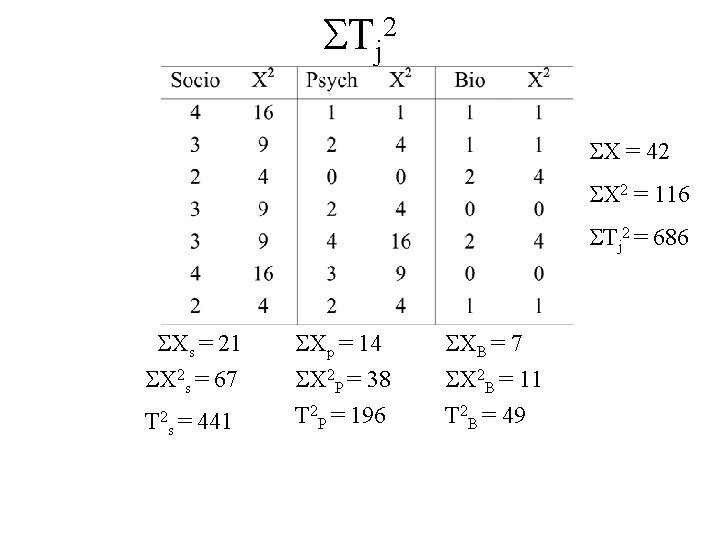
2 Tj X = 42 X 2 = 116 Tj 2 = 686 Xs = 21 X 2 s = 67 T 2 s = 441 Xp = 14 X 2 P = 38 T 2 P = 196 XB = 7 X 2 B = 11 T 2 B = 49

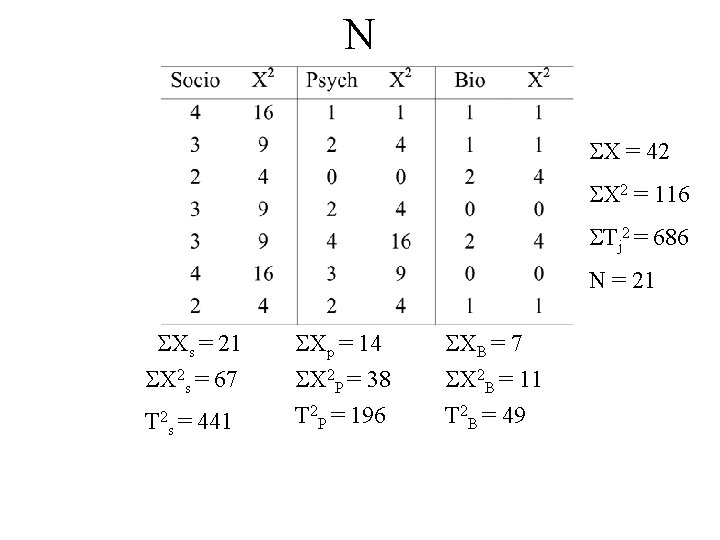
N X = 42 X 2 = 116 Tj 2 = 686 N = 21 Xs = 21 X 2 s = 67 T 2 s = 441 Xp = 14 X 2 P = 38 T 2 P = 196 XB = 7 X 2 B = 11 T 2 B = 49

n X = 42 X 2 = 116 Tj 2 = 686 N = 21 Xs = 21 X 2 s = 67 T 2 s = 441 Xp = 14 X 2 P = 38 T 2 P = 196 XB = 7 X 2 B = 11 T 2 B = 49 n=7

X = 42 Ingredients X 2 = 116 Tj 2 = 686 N = 21 n=7

X = 42 Calculate SS X 2 = 116 Tj 2 = 686 N = 21 • SStotal n=7

X = 42 Calculate SS X 2 = 116 Tj 2 = 686 N = 21 • SStotal 32 n=7 116 42 21

X = 42 Calculate SS X 2 = 116 Tj 2 = 686 • SSWithin N = 21 n=7

X = 42 Calculate SS X 2 = 116 Tj 2 = 686 • SSWithin N = 21 n=7 18 116 686 7

X = 42 Calculate SS X 2 = 116 Tj 2 = 686 • SSBetween N = 21 n=7

X = 42 Calculate SS X 2 = 116 Tj 2 = 686 • SSBetween N = 21 n=7 14 686 7 42 21

Sum of Squares • SSBetween • SSWithin • SStotal = SSBetween + SSWithin

Sum of Squares • SSBetween • SSWithin • SStotal • 32 = 14 + 18 = 14 = 18 = 32

Calculating the F value

Calculating the F value

Calculating the F value 7 14 2

Calculating the F value 7

Calculating the F value 7 1 18 18

Calculating the F value 7 7 1

How to write it out

Significance • Is an F value of 7. 0 significant at the. 05 level? • To find out you need to know both df

Degrees of Freedom • Dfbetween = k - 1 • dfwithin = N - k (k = number of groups) (N = total number of observations)

Degrees of Freedom • dfbetween = k - 1 • dfwithin = N - k • • 3 -1=2 21 - 3 = 18 Page 394 Table F dfbetween are in the numerator dfwithin are in the denominator Write this in the table

Critical F Value • F(2, 18) = 3. 55 • The nice thing about the F distribution is that everything is a one-tailed test

Decision • Thus, if F value > than F critical – Reject H 0, and accept H 1 • If F value < or = to F critical – Fail to reject H 0

Current Example • F value = 7. 00 • F critical = 3. 55 • Thus, reject H 0, and accept H 1

• Alternative hypothesis (H 1) H 1: The three population means are not all equal – In other words, psychology, sociology, and biology majors do not have equal class attendence – Notice: It does not say where this difference is at!!

How to write it out
