Lecture 16 Twofactor Analysis of Variance Chapter 15

















- Slides: 20

Lecture 16 • Two-factor Analysis of Variance (Chapter 15. 5) • Homework 4 has been posted. It is due Friday, March 21 st.

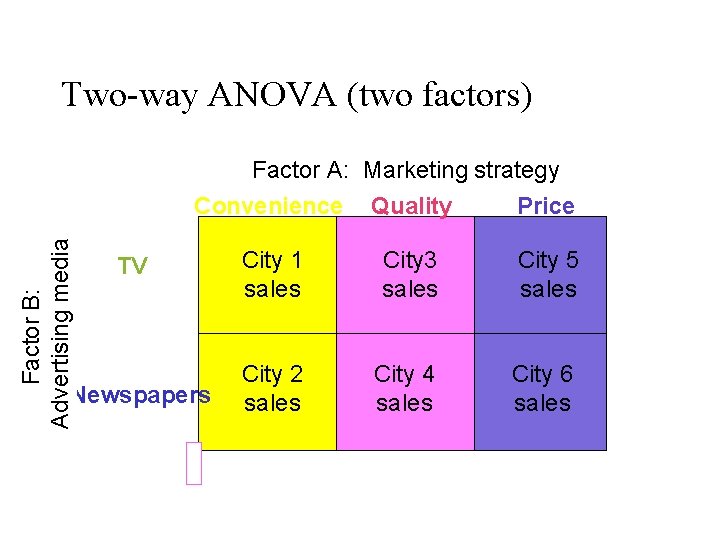
Two-way ANOVA (two factors) Factor B: Advertising media Factor A: Marketing strategy Convenience Quality Price TV Newspapers City 1 sales City 3 sales City 5 sales City 2 sales City 4 sales City 6 sales

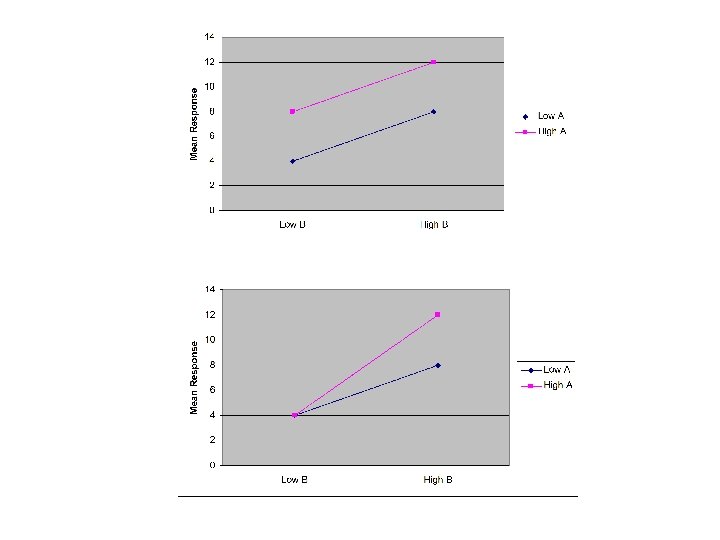
Main Effects • Marginal mean of level of factor A: The mean of the level of factor A across all levels of factor B. • The main effects of factor A refer to how the marginal means of levels of factor A change as the level of A change • In the absence of interactions, the main effects have a straightforward interpretation: What happens to the mean as we change the level of factor A and keep the level of factor B fixed.

Interactions • There is an interaction between A and B if the difference in means for the different levels of factor A changes as the level of factor B changes. • If there are interactions, the main effects no longer have a clear interpretation. Need to examine the means of all combinations of levels of A and B (e. g. , by using an interaction plot).


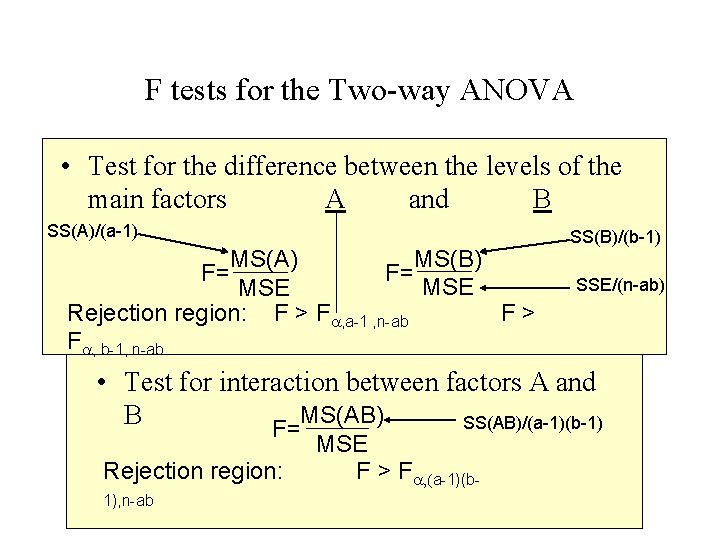
F tests for the Two-way ANOVA • Test for the difference between the levels of the main factors A and B SS(A)/(a-1) MS(B) MS(A) F= F= MSE Rejection region: F > Fa, a-1 , n-ab F> Fa, b-1, n-ab SS(B)/(b-1) SSE/(n-ab) • Test for interaction between factors A and MS(AB) B SS(AB)/(a-1)(b-1) F= Rejection region: 1), n-ab MSE F > Fa, (a-1)(b-

Required conditions: 1. The response distributions are normal 2. The treatment variances are equal. 3. The samples are independent simple random samples. Note: There a*b populations (and samples), one for each combination of levels of factor A and B.

F tests for the Two-way ANOVA • Example 15. 3 – continued( Xm 15 -03)

F tests for the Two-way ANOVA • Example 15. 3 – continued – Test of the difference in mean sales between the three marketing strategies H 0: mconv. = mquality = mprice H 1: At least two mean sales are different Factor A Marketing strategies

F tests for the Two-way ANOVA • Example 15. 3 – continued – Test of the difference in mean sales between the three marketing strategies H 0: mconv. = mquality = mprice H 1: At least two mean sales are different MS(A)/MSE F = MS(Marketing strategy)/MSE = 5. 33 Fcritical = Fa, a-1, n-ab = F. 05, 3 -1, 60 -(3)(2) = 3. 17; (p-value =. 0077) – At 5% significance level there is evidence to infer that differences in weekly sales exist among the marketing strategies.

F tests for the Two-way ANOVA • Example 15. 3 - continued – Test of the difference in mean sales between the two advertising media H 0: m. TV. = m. Nespaper H 1: The two mean sales differ Factor B = Advertising media

F tests for the Two-way ANOVA • Example 15. 3 - continued – Test of the difference in mean sales between the two advertising media H 0: m. TV. = m. Nespaper H 1: The two mean sales differ MS(B)/MSE F = MS(Media)/MSE = 1. 42 Fcritical = Fa, a-1, n-ab = F. 05, 2 -1, 60 -(3)(2) = 4. 02 (p-value =. 2387) – At 5% significance level there is insufficient evidence to infer that differences in weekly sales exist between the two advertising media.

F tests for the Two-way ANOVA • Example 15. 3 - continued – Test for interaction between factors A and B H 0: m. TV*conv. = m. TV*quality =…=mnewsp. *price H 1: At least two means differ Interaction AB = Marketing*Media

F tests for the Two-way ANOVA • Example 15. 3 - continued – Test for interaction between factor A and B H 0: m. TV*conv. = m. TV*quality =…=mnewsp. *price H 1: At least two means differ MS(AB)/MSE F = MS(Marketing*Media)/MSE =. 09 Fcritical = Fa, (a-1)(b-1), n-ab = F. 05, (3 -1)(2 -1), 60 -(3)(2) = 3. 17 (p-value=. 9171) – At 5% significance level there is insufficient evidence to infer that the two factors interact to affect the mean weekly sales.

Randomized Blocks vs. Two. Way ANOVA • The randomized block design is a special case of two-way ANOVA in which the blocks are the second factor and the number of replications is 1. • However, in analyzing a randomized blocks design, we assume that there are no interactions. • Also, in a randomized block design, blocking is specifically performed to reduce variation and there is no interest in the block effect itself. In the general two-way design, the effect of both of the factors is of interest.

Advantages of two-way ANOVA • When interested in studying the effects of two factors, two-way designs offer great advantages over several single-factor studies. • Example: Researchers want to determine the influence of dietary minerals on blood pressure. Rats receive diets prepared with varying amounts of calcium and varying amounts of magnesium, but with all other ingredients of the diets the same. There are three levels of calcium (low, medium and high) and three levels of magnesium.

Two Designs • Budget allows 90 rats to be studied. • Two-way design: Give each combination of calcium and magnesium to 9 rats (requires 81 total rats) • Two one-way designs: For the first experiment, give each of the three levels of calcium with a medium level of magnesium to 15 rats. For the second experiment, give each of the three levels of magnesium with a medium level of calcium to 15 rats (requires 90 total rats)

Advantages of two-way ANOVA • In two-way experiment, 27 rats are assigned to each of the three calcium diets. In the one-way experiment, there are only 15 rats assigned to each of the calcium diets. • For studying the marginal means of calcium, the two-way design can be more efficient because it is a “block” design with magnesium levels as blocks. • The two-way design allows interactions between calcium and magnesium to be studied.

Advantages of two-way designs compared to one-way designs • It is more efficient to study two factors simultaneously rather than separately. • For studying the effect of one factor, the two-way design is like a randomized block design and inherits block design’s advantages if second factor influences the response • We can investigate interactions between factors.

Practice Problems • 15. 48, 15. 72 • To format the data files, use cut and paste to copy labels. Then use tables, stack.