Analiza matematyczna I Informacje podstawowe WYKAD 2 Funkcje

Analiza matematyczna I. Informacje podstawowe WYKŁAD 2 Funkcje elementarne Krzysztof Kucab Rzeszów, 2012

Plan wykładu • • • zasada indukcji zupełnej, ciało liczb rzeczywistych, funkcje i działania na nich.

Zasada indukcji zupełnej to użyteczna metoda dowodzenia twierdzeń dotyczących liczb naturalnych. Zakładamy, że W(n) jest funkcją zdaniową, oraz n N Treść zasady indukcji zupełnej: • liczba 1 ma pewną własność W, (tzn. W(1) jest zdaniem prawdziwym); • jeśli w przypadku gdy pewna liczba naturalna n ma własność W to ma ją też jej następnik, (tzn. jeśli zachodzi implikacja W(n) W(n+1) ); to każda liczba naturalna n ma tę własność W.

Zasada indukcji zupełnej Przykłady: • Wykazać, że dla każdego naturalnego n liczba n 3 -n jest podzielna przez trzy. • Udowodnić, że dla każdego prawdą jest, że:

Teoria liczb rzeczywistych Liczby rzeczywiste można zdefiniować trzema sposobami: • aksjomatycznie, • metodą Cantora (przy pomocy ciągów Cauchy’ego liczb wymiernych), • metodą przekrojów Dedekinda.

Teoria liczb rzeczywistych Aksjomatyczna definicja liczb rzeczywistych 1. jest ciałem uporządkowanym, 2. Każdy niepusty zbiór ograniczony z góry ma kres górny.

Teoria liczb rzeczywistych Mówimy, że struktura algebraiczna jest ciałem uporządkowanym, gdy: 1. jest ciałem, 2. 3. lub w formie równoważnej: 1 a) (R, +, , 0, 1) jest ciałem, 2 a) 3 a) jeśli oraz 4 a) to

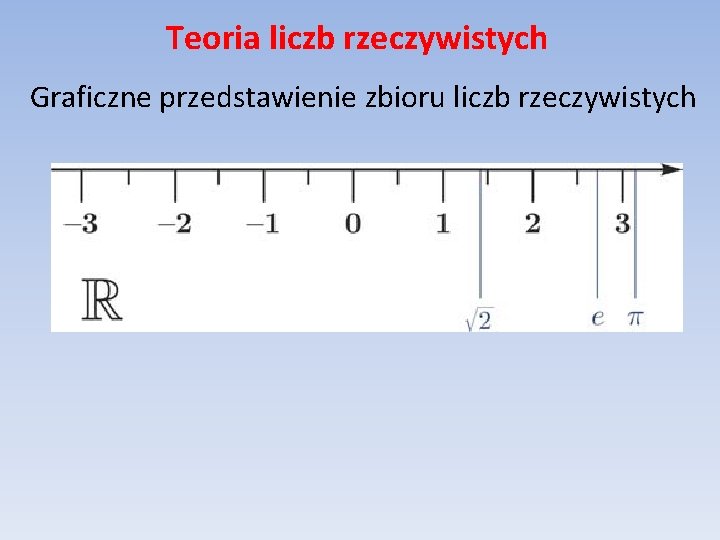
Teoria liczb rzeczywistych Graficzne przedstawienie zbioru liczb rzeczywistych

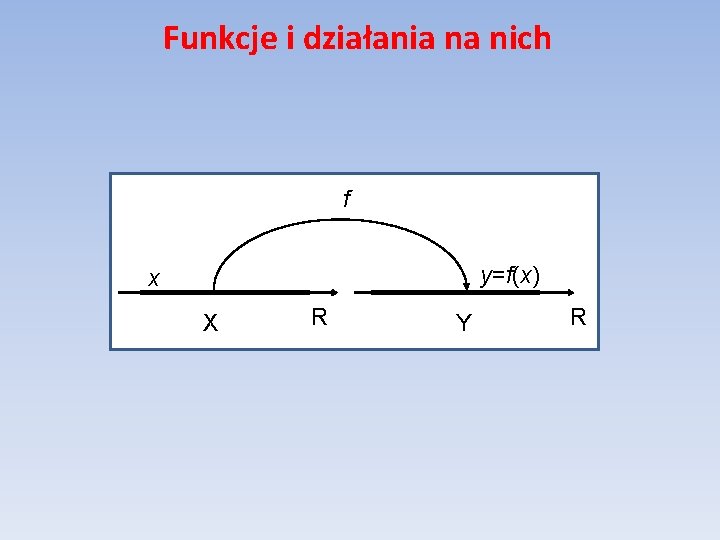
Funkcje i działania na nich Definicja funkcji Jeżeli każdej liczbie x określonej na zbiorze przyporządkowana jest dokładnie jedna liczba y to mówimy, że w zbiorze X określona jest funkcja zmiennej x. Zapisujemy to: Wielkość x nazywamy zmienną niezależną (argumentem funkcji), zaś y nazywamy zmienną zależną (wartością funkcji) f.

Funkcje i działania na nich f y=f(x) x X R Y R

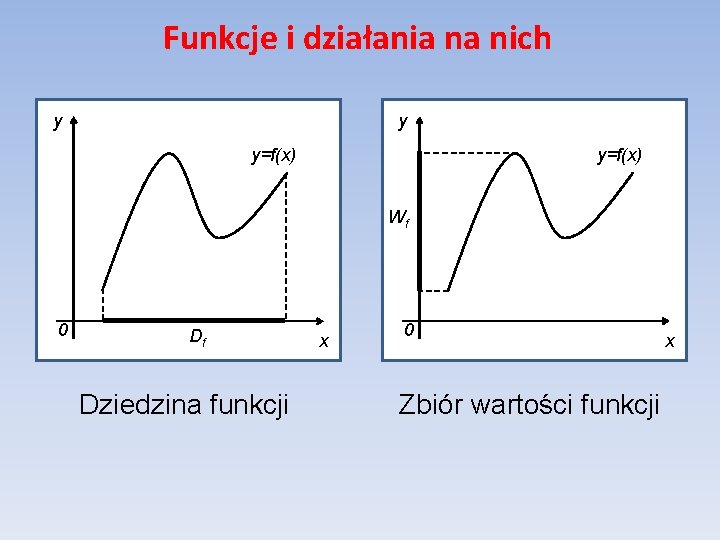
Funkcje i działania na nich Dziedzina i przeciwdziedzina funkcji Niech. Wtedy zbiór X nazywamy dziedziną funkcji f i oznaczamy przez Df zaś biór Y nazywamy przeciwdziedziną funkcji f. Zbiór nazywamy zbiorem wartości funkcji f i oznaczamy Wf. Dziedziną naturalną funkcji f nazywamy zbiór takich elementów ze zbioru R, dla których wzór określający funkcję ma sens, w przypadku gdy podany jest wyłącznie wzór funkcji.

Funkcje i działania na nich y y y=f(x) Wf 0 Df Dziedzina funkcji x 0 Zbiór wartości funkcji x

Funkcje i działania na nich Równość funkcji Dwie funkcje f oraz g określone następująco są sobie równe, tzn. f=g, gdy zachodzi:

Funkcje i działania na nich Wykres funkcji Wykresem funkcji y nazywamy zbiór: Wykres funkcji f y G y=f(x) Y 0 X x 0 Zbiór G nie jest wykresem funkcji x

Funkcje i działania na nich Funkcja „na” Funkcja f odwzorowuje zbiór X na zbiór Y, co zapisujemy jako w. t. w. , gdy: y y=f(x) Y 0 X x

Funkcje i działania na nich Funkcja okresowa jest okresowa, jeśli: Liczbę T nazywamy okresem funkcji f. Gdy istnieje najmniejszy okres funkcji f to nazywamy go okresem podstawowym tej funkcji.

Funkcje i działania na nich Funkcja parzysta jest parzysta, jeśli: y f(-x) = f(x) y=f(x) X -x 0 x x

Funkcje i działania na nich Funkcja nieparzysta jest nieparzysta, jeśli: y y=f(x) X -x 0 x f(-x) = -f(x) x

Funkcje i działania na nich Funkcja ograniczona Funkcja f jest ograniczona z dołu na zbiorze jeśli jej zbiór wartości na tym zbiorze jest ograniczony z dołu, tzn. : y A 0 f(x) m x y=f(x) x ,

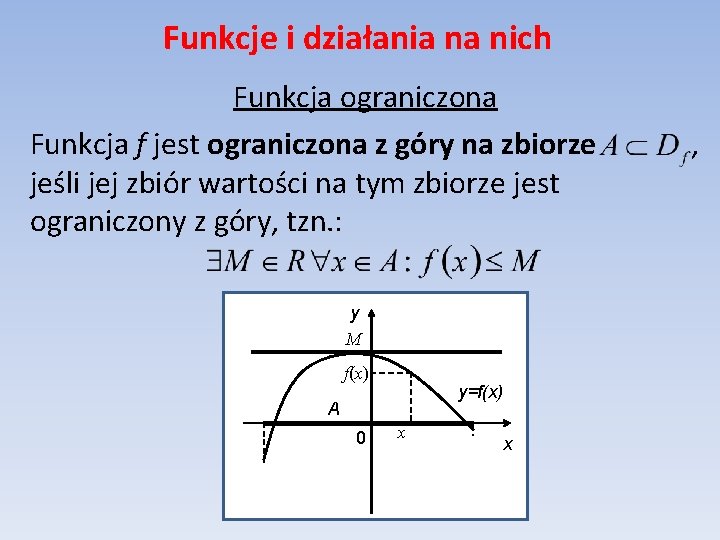
Funkcje i działania na nich Funkcja ograniczona Funkcja f jest ograniczona z góry na zbiorze jeśli jej zbiór wartości na tym zbiorze jest ograniczony z góry, tzn. : y M f(x) y=f(x) A 0 x x ,

Funkcje i działania na nich Funkcja ograniczona Funkcja f jest ograniczona na zbiorze , jeśli jest ograniczona z dołu i z góry na tym zbiorze, tzn. : y M f(x) y=f(x) A 0 m x x

Funkcje i działania na nich Funkcja monotoniczna Funkcja f jest rosnąca na zbiorze y=f(x) y f(x 2) f(x 1) x 1 0 A x 2 x , jeśli:

Funkcje i działania na nich Funkcja monotoniczna Funkcja f jest malejąca na zbiorze y x 1 0 A f(x 1) x 2 f(x 2) y=f(x) x , jeśli:

Funkcje i działania na nich Funkcja monotoniczna Funkcja f jest nierosnąca na zbiorze y x 1 0 A f(x 1) x 2 f(x 2) y=f(x) x , jeśli:

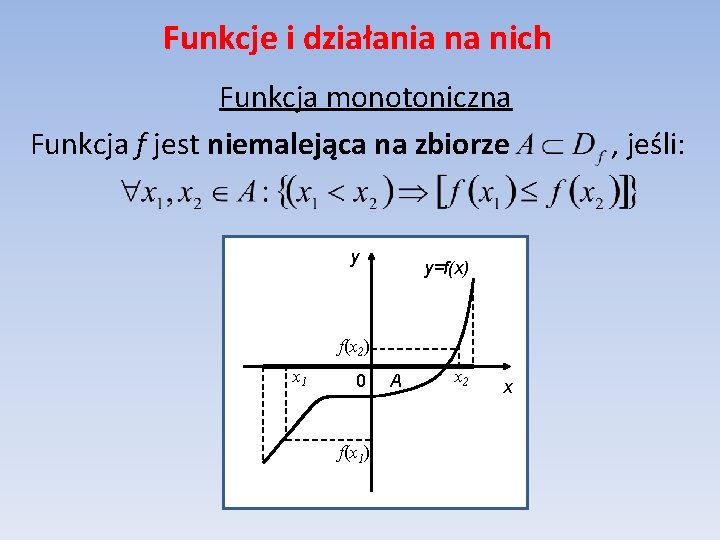
Funkcje i działania na nich Funkcja monotoniczna Funkcja f jest niemalejąca na zbiorze y y=f(x) f(x 2) x 1 0 f(x 1) A x 2 x , jeśli:

Funkcje i działania na nich Funkcja monotoniczna Funkcja jest monotoniczna na zbiorze, jeśli jest na tym zbiorze rosnąca, malejąca, nierosnąca lub niemalejąca. Funkcje rosnące i malejące nazywamy ściśle monotonicznymi. Funkcje nierosnące i niemalejące nazywamy słabo monotonicznymi.

Funkcje i działania na nich Funkcja monotoniczna Rodzaj monotoniczności funkcji f na zbiorze A ustalamy na podstawie znaku ilorazu: gdzie Znak ilorazu Rodzaj monotoniczności >0 funkcja rosnąca <0 funkcja malejąca 0 funkcja nierosnąca

Funkcje i działania na nich Funkcja złożona Niech X, Y, Z, W będą podzbiorami zbioru liczb rzeczywistych, przy czym oraz niech Złożeniem funkcji g i f nazywamy funkcję określoną wzorem: g f f g y x X Y=Z w W

Funkcje i działania na nich Funkcja odwrotna Funkcja f jest różnowartościowa na zbiorze jeśli: y=f(x) y f(x 2) f(x 1) x 1 0 A x 2 x

Funkcje i działania na nich Funkcja odwrotna Niech funkcja będzie różnowartościowa na dziedzinie. Funkcją odwrotną do f nazywamy funkcję określoną przez warunek: Źródło: M. Gewert, Z. Skoczylas, Analiza matematyczna 1, definicje, twierdzenia, wzory, Gi. S, Wrocław 2004.

Funkcje i działania na nich Niech funkcja Wtedy: Funkcja odwrotna będzie różnowartościowa.

Funkcje i działania na nich Funkcje elementarne Funkcjami elementarnymi nazywamy funkcje: • potęgowe, • wykładnicze, • trygonometryczne, • funkcje odwrotne względem powyższych, • ich sumy, różnice, iloczyny, ilorazy oraz superpozycje.

Funkcje i działania na nich Funkcje elementarne Funkcjami potęgowymi nazywamy funkcje: xn Dla n N funkcja potęgowa jest wielomianem. Funkcje odwrotne względem funkcji potęgowych nazywamy funkcjami pierwiastkowymi.

Funkcje i działania na nich Funkcje elementarne Funkcjami wykładniczymi nazywamy funkcje: y=ax , a>0 , a 1. Są określone w dziedzinie liczb rzeczywistych. Zbiorem wartości jest zbiór liczb rzeczywistych dodatnich (bez zera). Funkcje odwrotne względem funkcji wykładniczych nazywamy funkcjami logarytmicznymi y=logax , a>0 , a 1.

Funkcje i działania na nich Funkcje elementarne Funkcjami trygonometrycznymi nazywamy funkcje: y=sin x, y=cos x, y=tg x, y=ctg x. Są określone w dziedzinie liczb rzeczywistych. Funkcje odwrotne względem funkcji trygonometrycznych nazywamy funkcjami kołowymi (cyklometrycznymi) y=arcsinx , y=arccos x, y=arctg x, y=arcctg x.

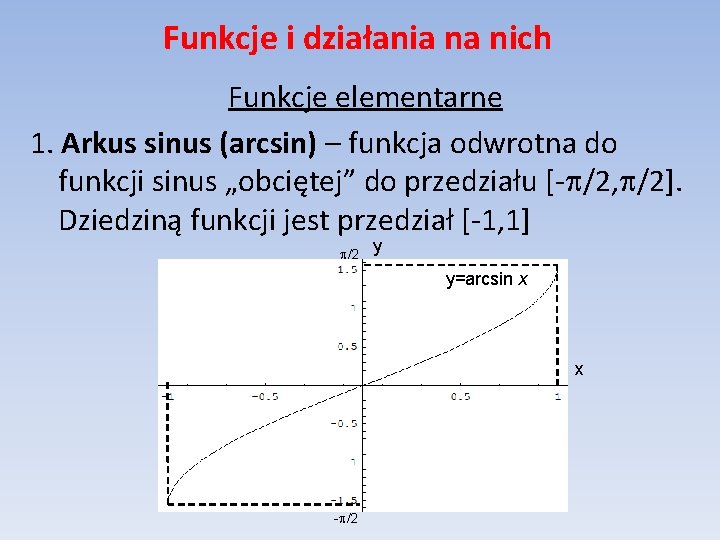
Funkcje i działania na nich Funkcje elementarne 1. Arkus sinus (arcsin) – funkcja odwrotna do funkcji sinus „obciętej” do przedziału [- /2, /2]. Dziedziną funkcji jest przedział [-1, 1] /2 y y=arcsin x x - /2

Funkcje i działania na nich Funkcje elementarne 2. Arkus kosinus (arccos) – funkcja odwrotna do funkcji kosinus „obciętej” do przedziału [0, ]. Dziedziną funkcji jest przedział [-1, 1] y y=arccos x 0 x

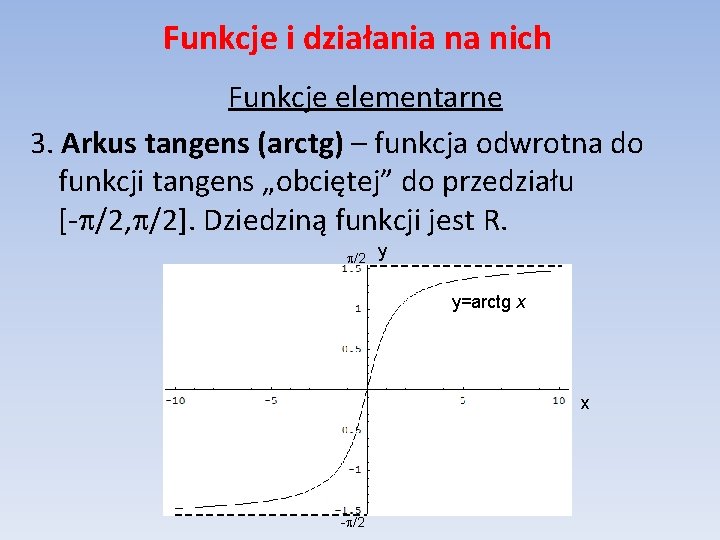
Funkcje i działania na nich Funkcje elementarne 3. Arkus tangens (arctg) – funkcja odwrotna do funkcji tangens „obciętej” do przedziału [- /2, /2]. Dziedziną funkcji jest R. /2 y y=arctg x x - /2

Funkcje i działania na nich Funkcje elementarne 4. Arkus kotangens (arcctg) – funkcja odwrotna do funkcji kotangens „obciętej” do przedziału [0, ]. Dziedziną funkcji jest R y /2 y=arcctg x x

Funkcje i działania na nich Funkcje elementarne Podstawowe tożsamości dla funkcji cyklometrycznych:

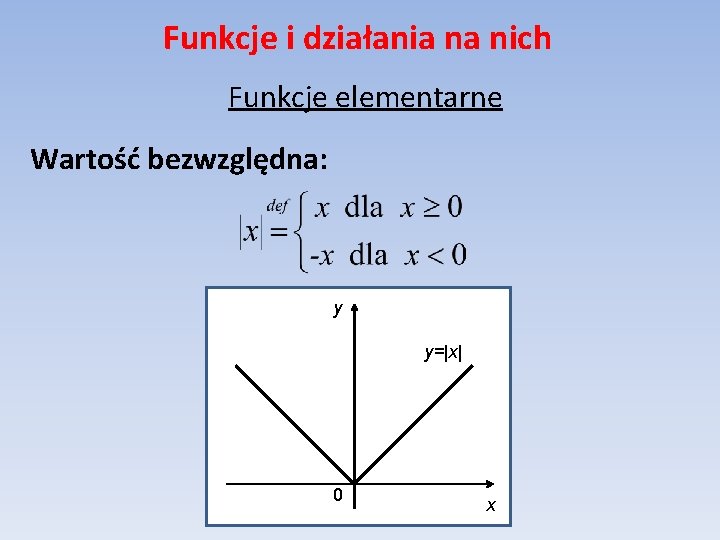
Funkcje i działania na nich Funkcje elementarne Wartość bezwzględna: y y=|x| 0 x

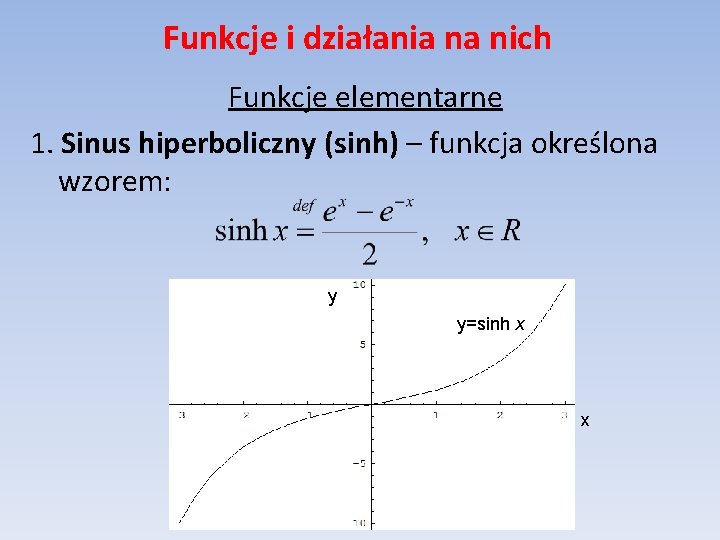
Funkcje i działania na nich Funkcje elementarne 1. Sinus hiperboliczny (sinh) – funkcja określona wzorem: y y=sinh x x

Funkcje i działania na nich Funkcje elementarne 2. Kosinus hiperboliczny (cosh) – funkcja określona wzorem: y y=cosh x x

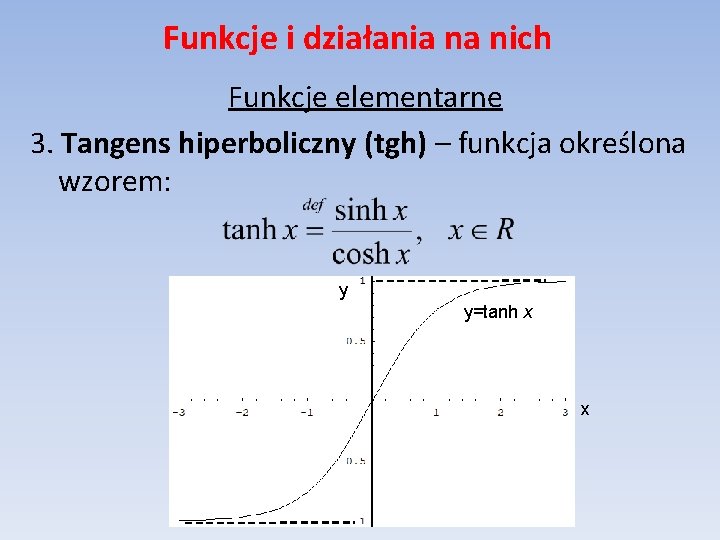
Funkcje i działania na nich Funkcje elementarne 3. Tangens hiperboliczny (tgh) – funkcja określona wzorem: y y=tanh x x

Funkcje i działania na nich Funkcje elementarne 4. Kotangens hiperboliczny (ctgh) – funkcja określona wzorem: y y=coth x 1 x -1

Funkcje i działania na nich Funkcje elementarne Podstawowe tożsamości dla funkcji hiperbolicznych: