Advance Quantum Chemistry Atomic Structure and Spectra FMIPA

Advance Quantum Chemistry : Atomic Structure and Spectra FMIPA UGM – 11 March 2020 Niko Prasetyo

Outline Atomic structure and spectra – Hydrogenic atom – Atomic orbital – Spectra of electronic transitions and selection rules : ( Structures of many electron system – The approximations – SCF orbitals Spectra of complex system Molecular structure – – VBT, MO theory Hückel approximation 2

Outline Spectra of complex system – – Some terminologies Singlet and triplet states Spin – orbit coupling Term symbol and selection rule (again : ( ) 3

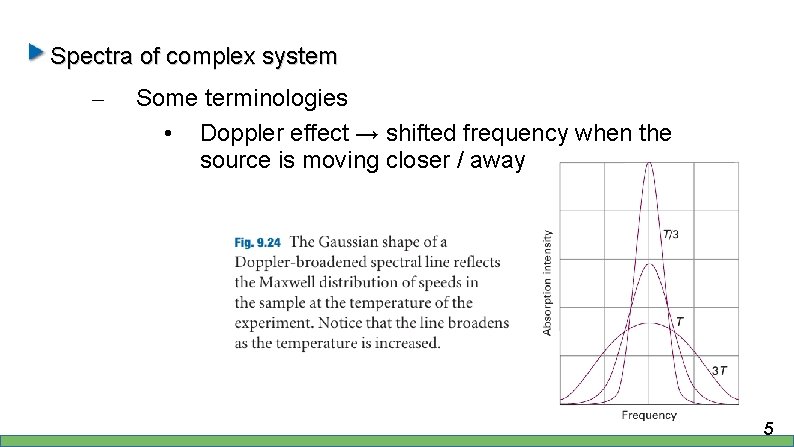
Spectra of complex system – Some terminologies • Doppler effect → shifted frequency when the source is moving closer / away 4

Spectra of complex system – Some terminologies • Doppler effect → shifted frequency when the source is moving closer / away 5

Spectra of complex system – Some terminologies • Doppler effect → shifted frequency when the source is moving closer / away • Doppler effect is proportional with T, thus to reduce this effect, we have work with cool sample 6

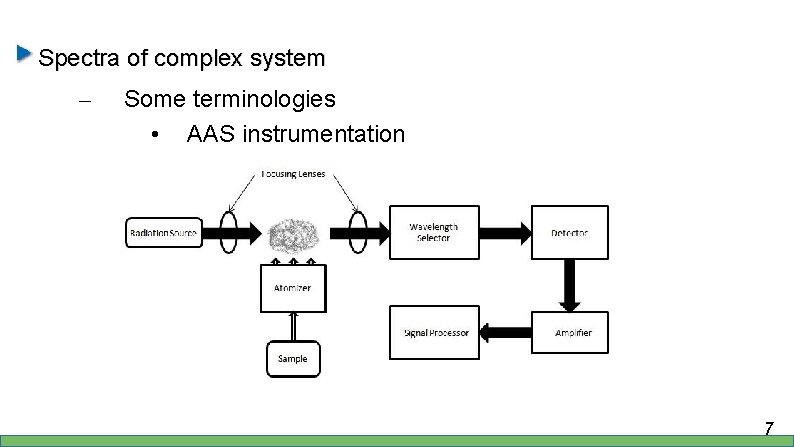
Spectra of complex system – Some terminologies • AAS instrumentation 7

Spectra of complex system – Some terminologies • AAS instrumentation – Sample → atomizer → radiation → detector etc… • In radiation process, the atom is excited from ground to excited states, back to ground states with emitted energy • Which mean, the lifetime of excited states are limited 8

Spectra of complex system – Important concept when dealing with atomic spectroscopy is singlet and triplet states • Differs in energy, reactivity and so on 9

Spectra of complex system – – – If we look the configuration electron of He (1 s 2). In ground state all of the electron is paired (singlet) If the electron is excited now we have 1 s 1 2 s 1 (triplet) we can express the triplet states as 10

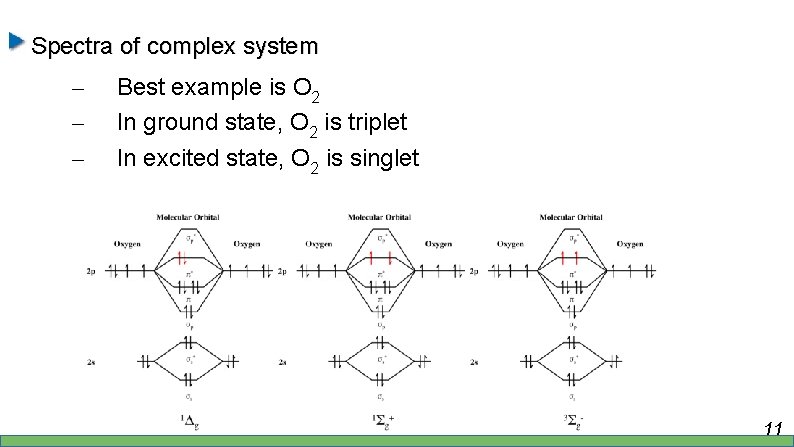
Spectra of complex system – – – Best example is O 2 In ground state, O 2 is triplet In excited state, O 2 is singlet 11

Spectra of complex system – Spin-orbit coupling • Interaction of the spin magnetic moment with the magnetic field arising from the orbital angular momentum • Relative to orientation of the spin and orbital momenta 12

13

Spectra of complex system – – – One simplest way to express the spin-orbit coupling is via total momentum angular (j) j = l + ½ or l – ½ Example d 1 will have j = 5/2 and 3/2. s 1 will only have ½. p 1 will have 3/2 and ½ and f 1 will have 7/2 and 5/2 As far as I remember, you will find j in NMR 14

Spectra of complex system – Energy of each states can be defined as – For example in alkali metal ions, the unpaired electron will sit in s 1. So the l=0 and j = ½ – Energy at this state is ½ hc. A – When the electron is excited to p 1 , the energy will be -hc. A 15

Spectra of complex system – – After we understand j, now we are ready to begin the term symbol and selection rule In term symbol, the lower case letter is used to label the orbital (s, p, d, f) and the upper case is used to label overall states What is the states ? And why we have to use different label ? Let see this example. . . 16

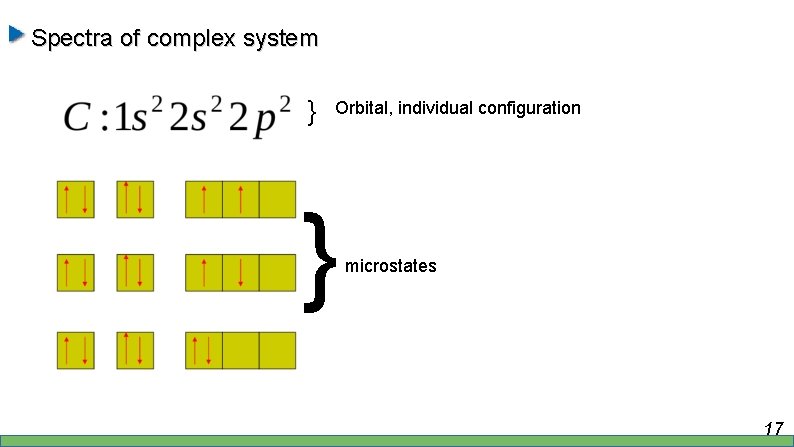
Spectra of complex system } Orbital, individual configuration } microstates 17

Spectra of complex system – – Term symbol accounts the sum of microstates via notation J is total angular momentum L is total ORBITAL angular momentum S is total SPIN angular momentum 18

Spectra of complex system x If all l are equal, the minimum is zero, if one l is larger than the others, the minimum is that given by orienting the other angular momentum to oppose it as long as L>= 0. (vector sum of all vector l. I). 19

Spectra of complex system 20

Spectra of complex system – Example : • Derive the term symbol for ground state of Na, F and excited configuration of C (1 s 22 p 13 p 1) • Answer : – Ignore the closed shells – Couple l to find L – Couple s to find S – Couple L and S to find J – Write the 2 S+1 LJ formula 21

Spectra of complex system – Example : • Na – [Ne] 3 s 1. – L = l = 0, S = s = ½ , J = j = s = ½ 2 S 1/2 • F – [He] 2 s 2 2 p 5 or [Ne] 2 p-1 – L = 1, S = s = ½, J= 3/2, ½ – 2 P 3/2 , 2 P 1/2 22

Spectra of complex system – Example : • C 1 s 22 p 13 p 1 – Basically is 2 electrons problem. – l 1 = l 2 = 1 – L = 2, 1, 0 – s 1 = s 2 = ½ – S = 1, 0 – J = 3, 2, 1 23

Therefore, we have 2 S+1 L LJ 24

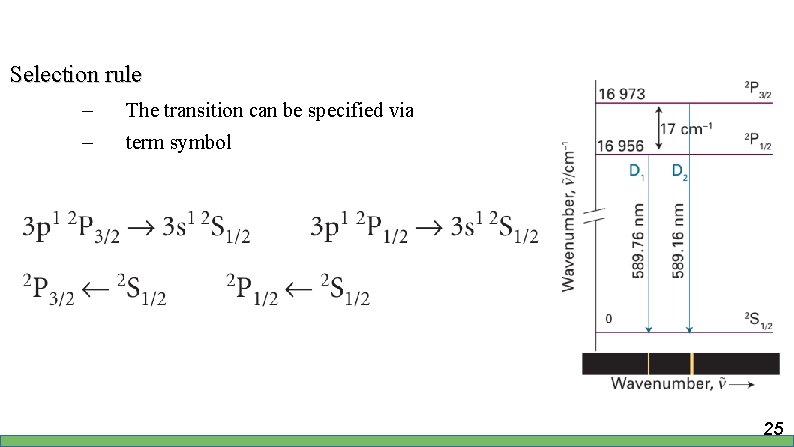
Selection rule – – The transition can be specified via term symbol 25

Selection rule – – Arises from conservation of angular momentum during transition Photon has spin 1 Denotes the forbidden transition 26

Which of the following transitions are allowed in the normal electronic emission spectrum of an atom: (a) 5 d → 2 s, (b) 5 p → 3 s, (c) 6 p → 4 f? a) not allowed, Δl = -2 b) allowed Δl = -1 c) not allowed Δl = 2 27

Write the electronic configuration of the V 2+ ion. (b) What are the possible values of the total spin quantum numbers S and MS for this ion? 28