7 TECHNIQUES OF INTEGRATION TECHNIQUES OF INTEGRATION There








![APPROXIMATE INTEGRATION If we divide [a, b] into n subintervals of equal length ∆x APPROXIMATE INTEGRATION If we divide [a, b] into n subintervals of equal length ∆x](https://slidetodoc.com/presentation_image_h2/5080c650bb887897c909991ae564e7b5/image-9.jpg)




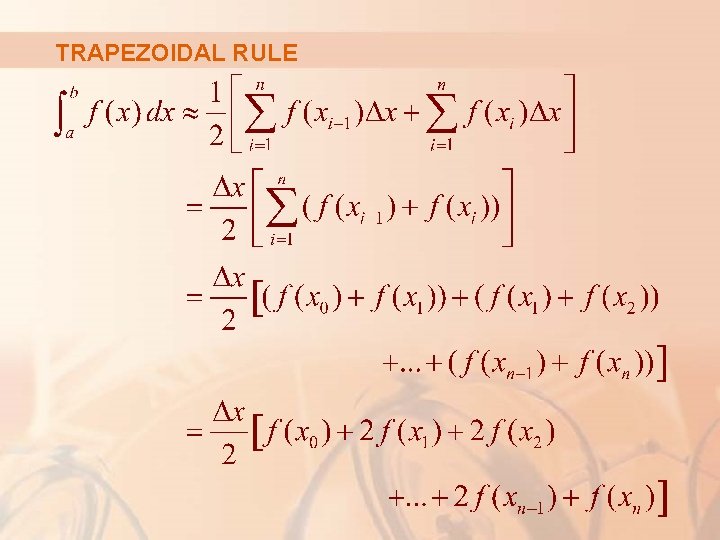

































![APPROXIMATE INTEGRATION As before, we divide [a, b] into n subintervals of equal length APPROXIMATE INTEGRATION As before, we divide [a, b] into n subintervals of equal length](https://slidetodoc.com/presentation_image_h2/5080c650bb887897c909991ae564e7b5/image-62.jpg)









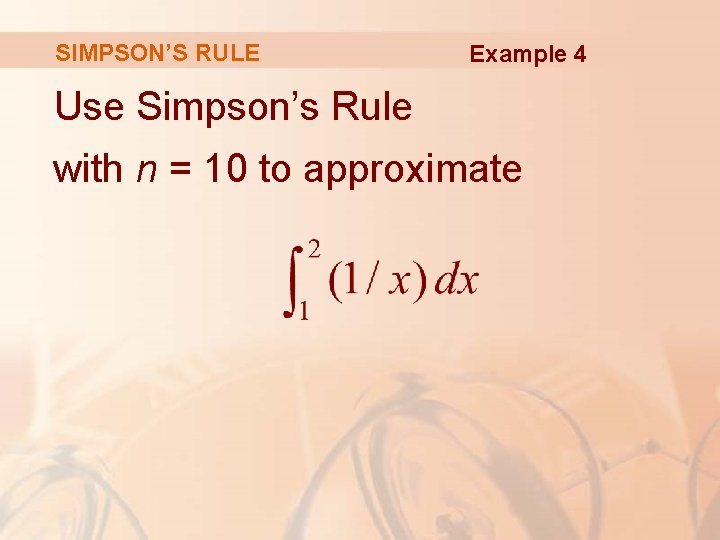




















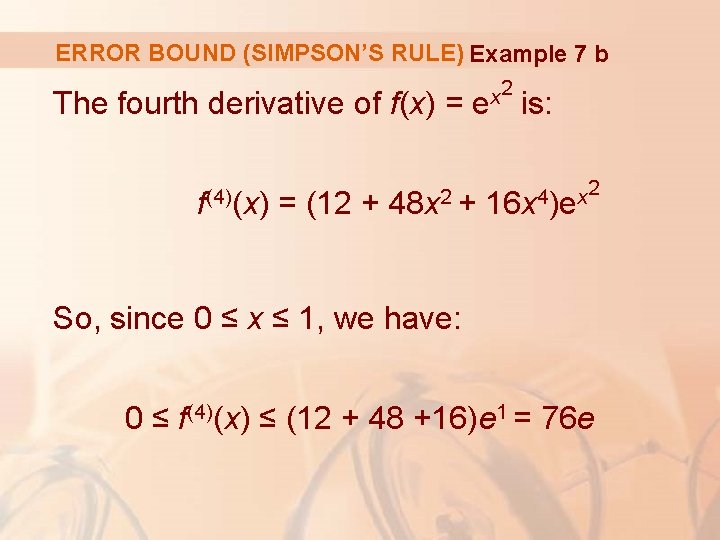


- Slides: 102

7 TECHNIQUES OF INTEGRATION

TECHNIQUES OF INTEGRATION There are two situations in which it is impossible to find the exact value of a definite integral.

TECHNIQUES OF INTEGRATION The first situation arises from the fact that, in order to evaluate using the Fundamental Theorem of Calculus (FTC), we need to know an antiderivative of f.

TECHNIQUES OF INTEGRATION However, sometimes, it is difficult, or even impossible, to find an antiderivative (Section 7. 5). § For example, it is impossible to evaluate the following integrals exactly:

TECHNIQUES OF INTEGRATION The second situation arises when the function is determined from a scientific experiment through instrument readings or collected data. § There may be no formula for the function (as we will see in Example 5).

TECHNIQUES OF INTEGRATION In both cases, we need to find approximate values of definite integrals.

TECHNIQUES OF INTEGRATION 7. 7 Approximate Integration In this section, we will learn: How to find approximate values of definite integrals.

APPROXIMATE INTEGRATION We already know one method for approximate integration. § Recall that the definite integral is defined as a limit of Riemann sums. § So, any Riemann sum could be used as an approximation to the integral.
![APPROXIMATE INTEGRATION If we divide a b into n subintervals of equal length x APPROXIMATE INTEGRATION If we divide [a, b] into n subintervals of equal length ∆x](https://slidetodoc.com/presentation_image_h2/5080c650bb887897c909991ae564e7b5/image-9.jpg)
APPROXIMATE INTEGRATION If we divide [a, b] into n subintervals of equal length ∆x = (b – a)/n, we have: where xi* is any point in the i th subinterval [xi -1, xi].

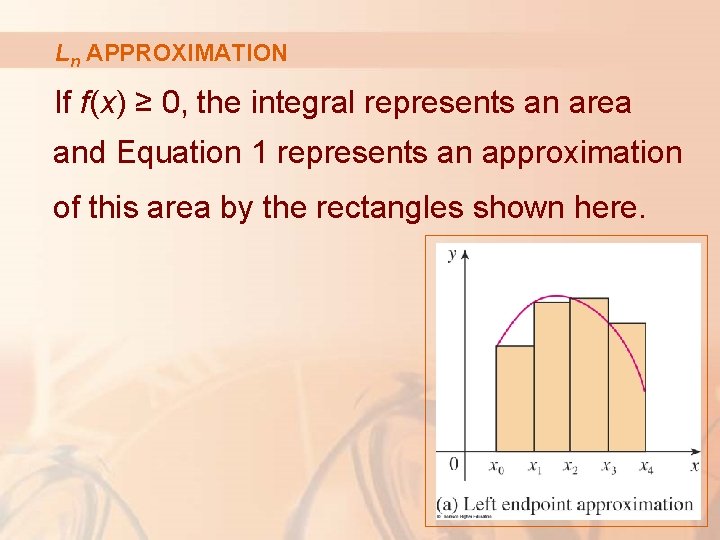
Ln APPROXIMATION Equation 1 If xi* is chosen to be the left endpoint of the interval, then xi* = xi -1 and we have: § The approximation Ln is called the left endpoint approximation.

Ln APPROXIMATION If f(x) ≥ 0, the integral represents an area and Equation 1 represents an approximation of this area by the rectangles shown here.

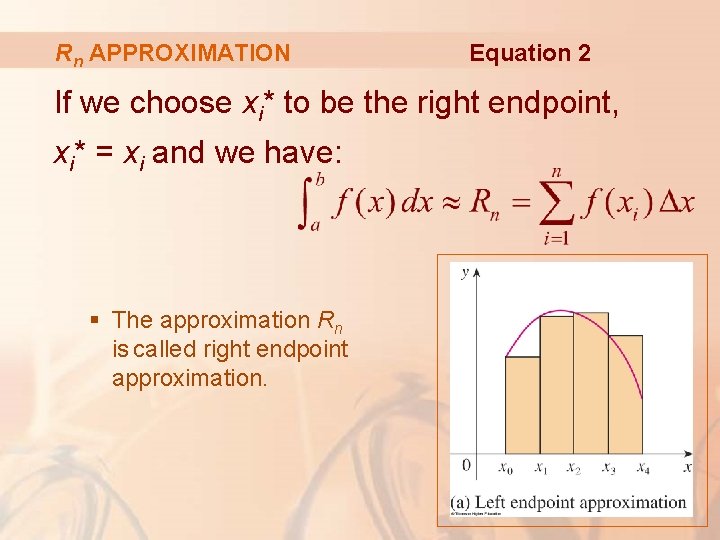
Rn APPROXIMATION Equation 2 If we choose xi* to be the right endpoint, xi* = xi and we have: § The approximation Rn is called right endpoint approximation.

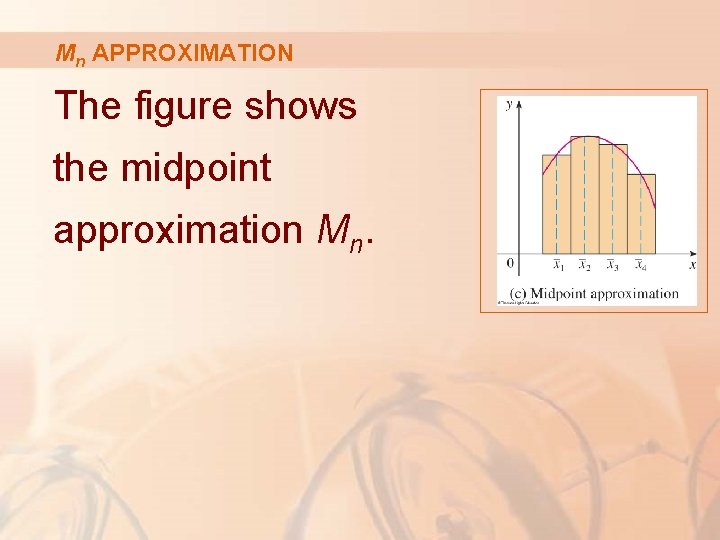
APPROXIMATE INTEGRATION In Section 5. 2, we also considered the case where xi* is chosen to be the midpoint of the subinterval [xi -1, xi].

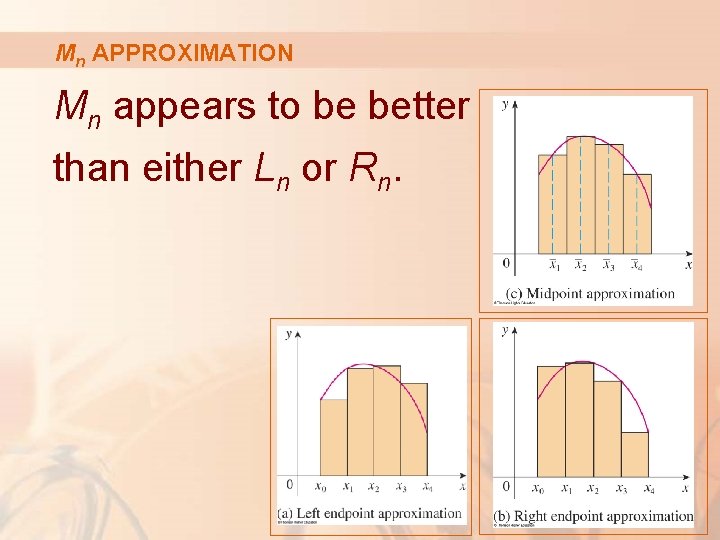
Mn APPROXIMATION The figure shows the midpoint approximation Mn.

Mn APPROXIMATION Mn appears to be better than either Ln or Rn.

THE MIDPOINT RULE where and

TRAPEZOIDAL RULE Another approximation—called the Trapezoidal Rule—results from averaging the approximations in Equations 1 and 2, as follows.
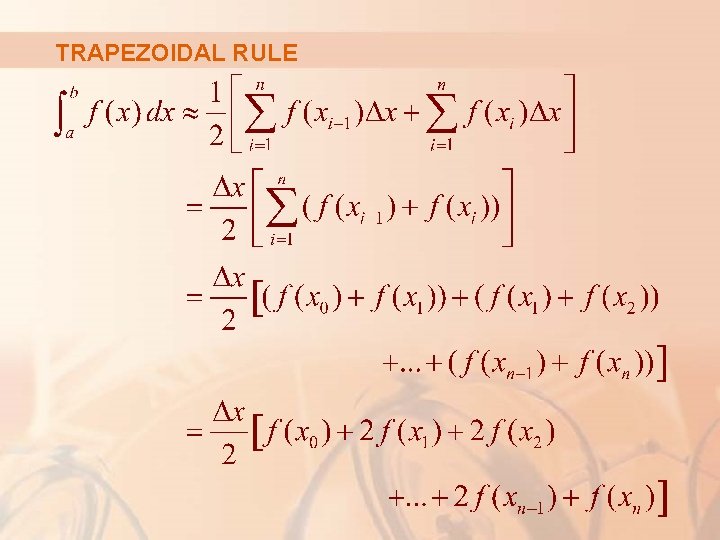
TRAPEZOIDAL RULE

THE TRAPEZOIDAL RULE where ∆x = (b – a)/n and xi = a + i ∆x

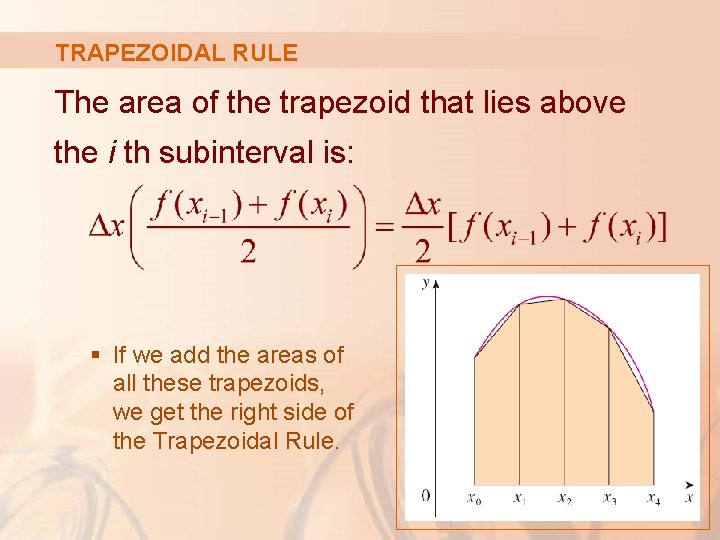
TRAPEZOIDAL RULE The reason for the name can be seen from the figure, which illustrates the case f(x) ≥ 0.

TRAPEZOIDAL RULE The area of the trapezoid that lies above the i th subinterval is: § If we add the areas of all these trapezoids, we get the right side of the Trapezoidal Rule.

APPROXIMATE INTEGRATION Approximate the integral with n = 5, using: a. Trapezoidal Rule b. Midpoint Rule Example 1

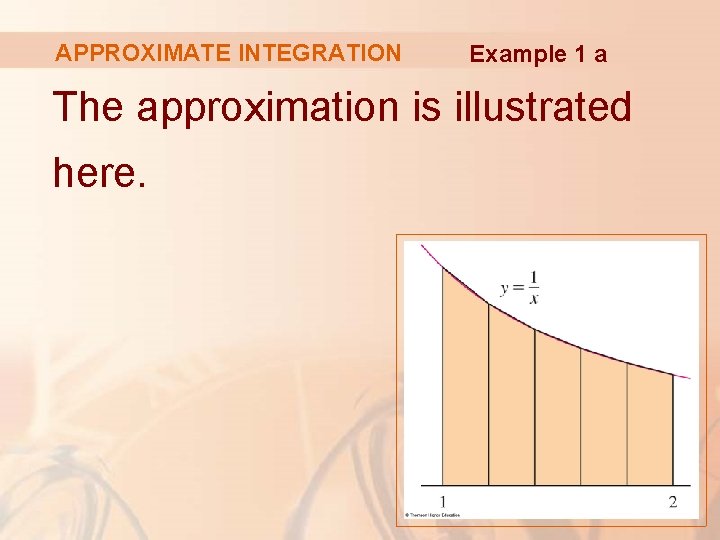
APPROXIMATE INTEGRATION With n = 5, a = 1 and b = 2, we have: ∆x = (2 – 1)/5 = 0. 2 § So, the Trapezoidal Rule gives: Example 1 a

APPROXIMATE INTEGRATION Example 1 a The approximation is illustrated here.

APPROXIMATE INTEGRATION Example 1 b The midpoints of the five subintervals are: 1. 1, 1. 3, 1. 5, 1. 7, 1. 9

APPROXIMATE INTEGRATION So, the Midpoint Rule gives: Example 1 b

APPROXIMATE INTEGRATION In Example 1, we deliberately chose an integral whose value can be computed explicitly so that we can see how accurate the Trapezoidal and Midpoint Rules are. § By the FTC,

APPROXIMATION ERROR The error in using an approximation is defined as the amount that needs to be added to the approximation to make it exact.

APPROXIMATE INTEGRATION From the values in Example 1, we see that the errors in the Trapezoidal and Midpoint Rule approximations for n = 5 are: ET ≈ – 0. 002488 EM ≈ 0. 001239

APPROXIMATE INTEGRATION In general, we have:

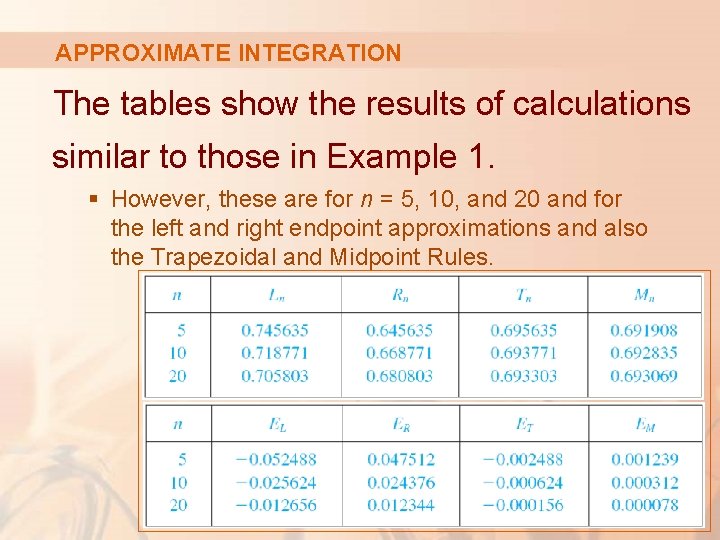
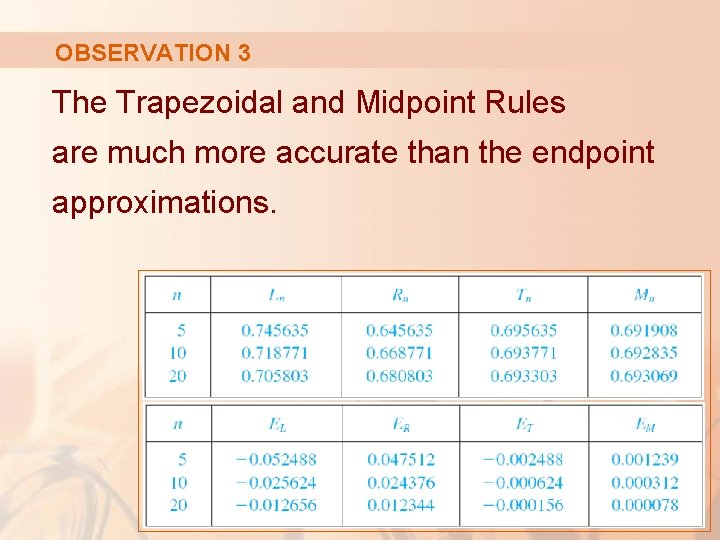
APPROXIMATE INTEGRATION The tables show the results of calculations similar to those in Example 1. § However, these are for n = 5, 10, and 20 and for the left and right endpoint approximations and also the Trapezoidal and Midpoint Rules.

APPROXIMATE INTEGRATION We can make several observations from these tables.

OBSERVATION 1 In all the methods. we get more accurate approximations when we increase n. § However, very large values of n result in so many arithmetic operations that we have to beware of accumulated round-off error.

OBSERVATION 2 The errors in the left and right endpoint approximations are: § Opposite in sign § Appear to decrease by a factor of about 2 when we double the value of n

OBSERVATION 3 The Trapezoidal and Midpoint Rules are much more accurate than the endpoint approximations.

OBSERVATION 4 The errors in the Trapezoidal and Midpoint Rules are: § Opposite in sign § Appear to decrease by a factor of about 4 when we double the value of n

OBSERVATION 5 The size of the error in the Midpoint Rule is about half that in the Trapezoidal Rule.

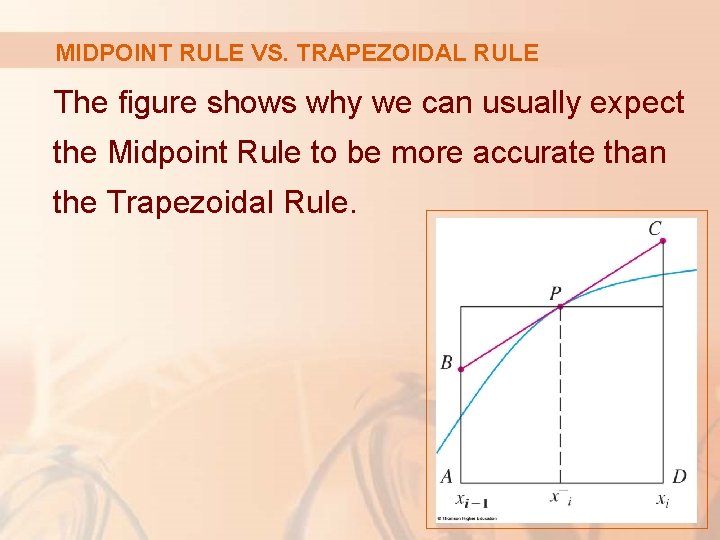
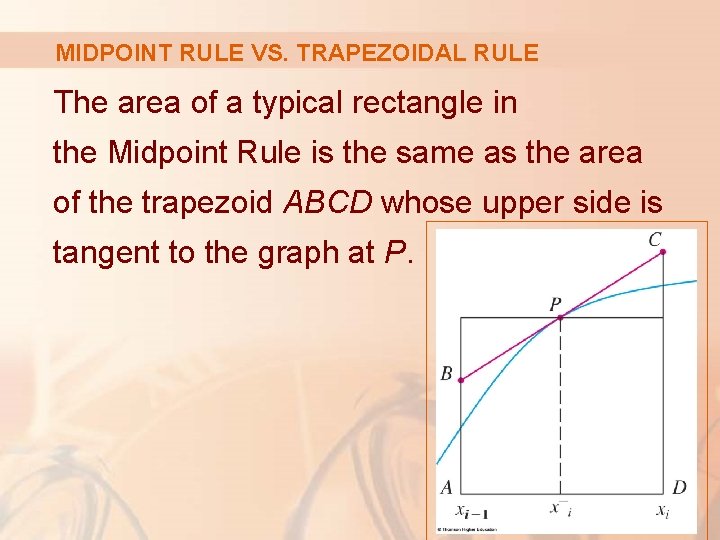
MIDPOINT RULE VS. TRAPEZOIDAL RULE The figure shows why we can usually expect the Midpoint Rule to be more accurate than the Trapezoidal Rule.

MIDPOINT RULE VS. TRAPEZOIDAL RULE The area of a typical rectangle in the Midpoint Rule is the same as the area of the trapezoid ABCD whose upper side is tangent to the graph at P.

MIDPOINT RULE VS. TRAPEZOIDAL RULE The area of this trapezoid is closer to the area under the graph than is the area of that used in the Trapezoidal Rule.

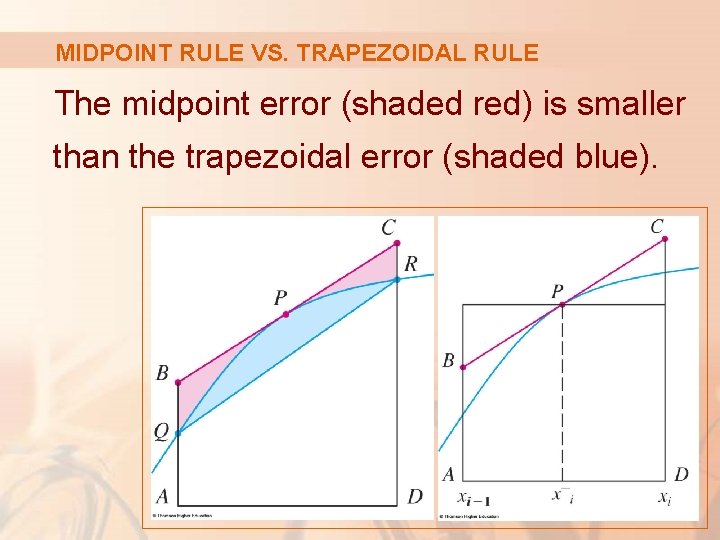
MIDPOINT RULE VS. TRAPEZOIDAL RULE The midpoint error (shaded red) is smaller than the trapezoidal error (shaded blue).

OBSERVATIONS These observations are corroborated in the following error estimates—which are proved in books on numerical analysis.

OBSERVATIONS Notice that Observation 4 corresponds to the n 2 in each denominator because: (2 n)2 = 4 n 2

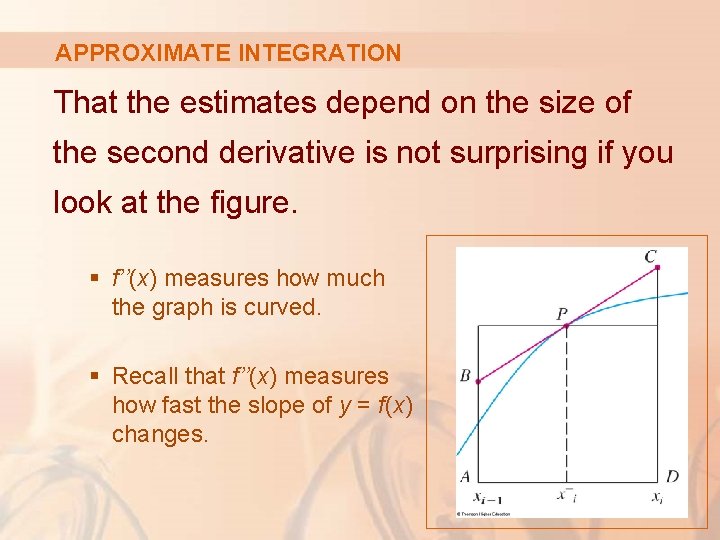
APPROXIMATE INTEGRATION That the estimates depend on the size of the second derivative is not surprising if you look at the figure. § f’’(x) measures how much the graph is curved. § Recall that f’’(x) measures how fast the slope of y = f(x) changes.

ERROR BOUNDS Estimate 3 Suppose | f’’(x) | ≤ K for a ≤ x ≤ b. If ET and EM are the errors in the Trapezoidal and Midpoint Rules, then

ERROR BOUNDS Let’s apply this error estimate to the Trapezoidal Rule approximation in Example 1. § If f(x) = 1/x, then f’(x) = -1/x 2 and f’’(x) = 2/x 3. § As 1 ≤ x ≤ 2, we have 1/x ≤ 1; so,

ERROR BOUNDS So, taking K = 2, a = 1, b = 2, and n = 5 in the error estimate (3), we see:

ERROR BOUNDS Comparing this estimate with the actual error of about 0. 002488, we see that it can happen that the actual error is substantially less than the upper bound for the error given by (3).

ERROR ESTIMATES Example 2 How large should we take n in order to guarantee that the Trapezoidal and Midpoint Rule approximations for accurate to within 0. 0001? are

ERROR ESTIMATES Example 2 We saw in the preceding calculation that | f’’(x) | ≤ 2 for 1 ≤ x ≤ 2 § So, we can take K = 2, a = 1, and b = 2 in (3).

ERROR ESTIMATES Example 2 Accuracy to within 0. 0001 means that the size of the error should be less than 0. 0001 § Therefore, we choose n so that:

ERROR ESTIMATES Solving the inequality for n, we get or § Thus, n = 41 will ensure the desired accuracy. Example 2

ERROR ESTIMATES Example 2 It’s quite possible that a lower value for n would suffice. § However, 41 is the smallest value for which the error-bound formula can guarantee us accuracy to within 0. 0001

ERROR ESTIMATES Example 2 For the same accuracy with the Midpoint Rule, we choose n so that: This gives:

ERROR ESTIMATES Example 3 a. Use the Midpoint Rule with n = 10 to approximate the integral b. Give an upper bound for the error involved in this approximation.

ERROR ESTIMATES Example 3 a As a = 0, b = 1, and n = 10, the Midpoint Rule gives:

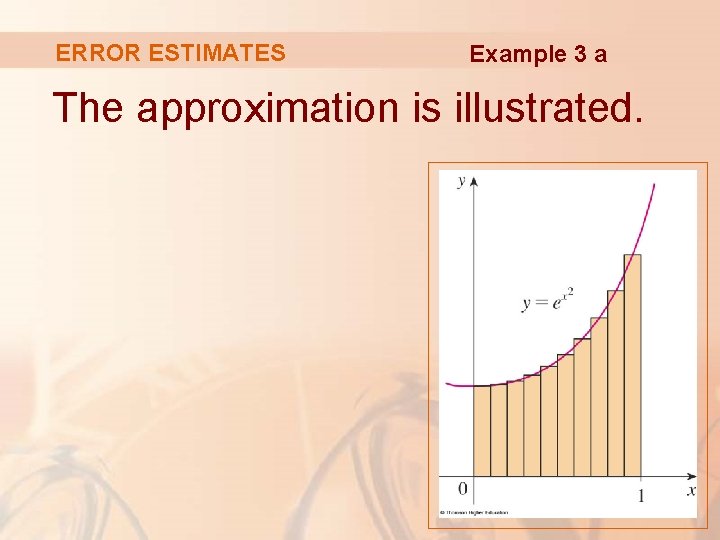
ERROR ESTIMATES Example 3 a The approximation is illustrated.

ERROR ESTIMATES As f(x) = 2 x e , f’(x) = Example 3 b we have: 2 x 2 xe and f’’(x) = (2 + 2 2 x 4 x )e Also, since 0 ≤ x ≤ 1, we have x 2 ≤ 1. Hence, 0 ≤ f’’(x) = (2 + 4 x 2) 2 x e ≤ 6 e

ERROR ESTIMATES Example 3 b Taking K = 6 e, a = 0, b = 1, and n = 10 in the error estimate (3), we see that an upper bound for the error is:

ERROR ESTIMATES Error estimates give upper bounds for the error. § They are theoretical, worst-case scenarios. § The actual error in this case turns out to be about 0. 0023

APPROXIMATE INTEGRATION Another rule for approximate integration results from using parabolas instead of straight line segments to approximate a curve.
![APPROXIMATE INTEGRATION As before we divide a b into n subintervals of equal length APPROXIMATE INTEGRATION As before, we divide [a, b] into n subintervals of equal length](https://slidetodoc.com/presentation_image_h2/5080c650bb887897c909991ae564e7b5/image-62.jpg)
APPROXIMATE INTEGRATION As before, we divide [a, b] into n subintervals of equal length h = ∆x = (b – a)/n. However, this time, we assume n is an even number.

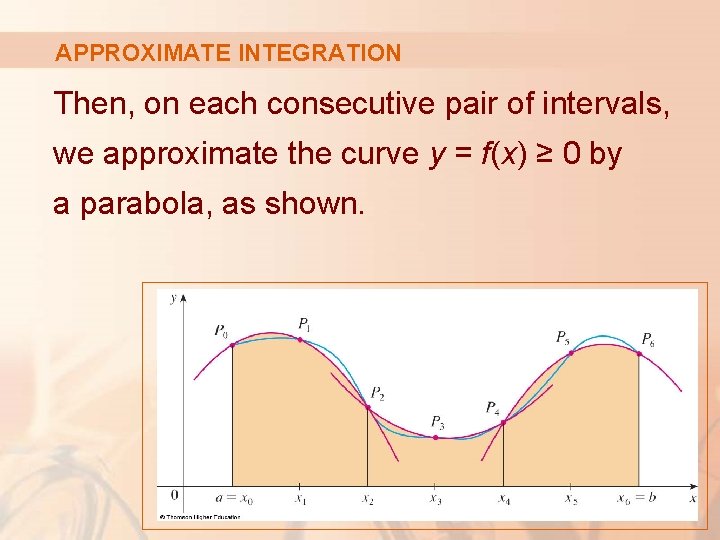
APPROXIMATE INTEGRATION Then, on each consecutive pair of intervals, we approximate the curve y = f(x) ≥ 0 by a parabola, as shown.

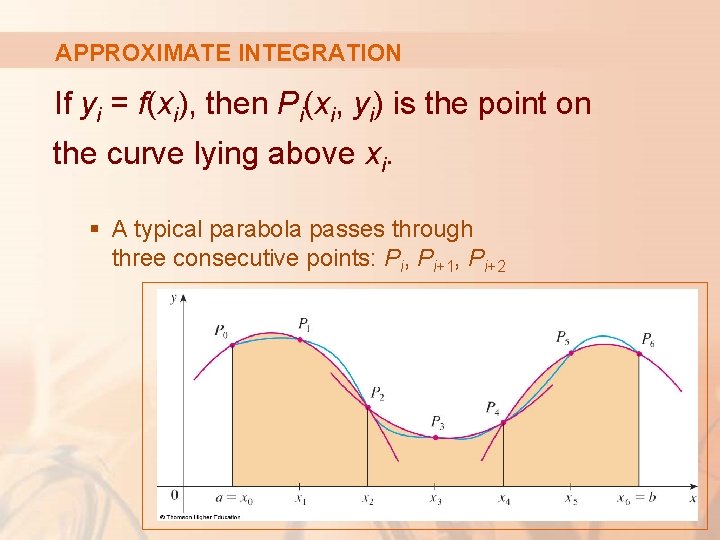
APPROXIMATE INTEGRATION If yi = f(xi), then Pi(xi, yi) is the point on the curve lying above xi. § A typical parabola passes through three consecutive points: Pi, Pi+1, Pi+2

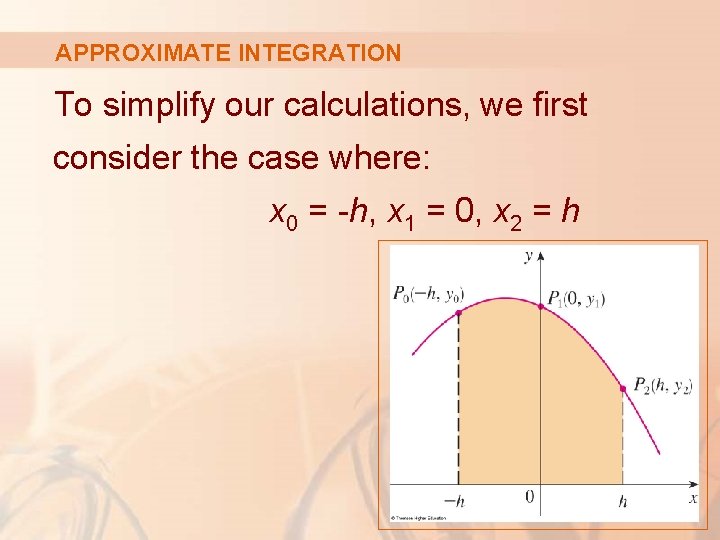
APPROXIMATE INTEGRATION To simplify our calculations, we first consider the case where: x 0 = -h, x 1 = 0, x 2 = h

APPROXIMATE INTEGRATION We know that the equation of the parabola through P 0, P 1, and P 2 is of the form y = Ax 2 + Bx + C

APPROXIMATE INTEGRATION Therefore, the area under the parabola from x = - h to x = h is:

APPROXIMATE INTEGRATION However, as the parabola passes through P 0(- h, y 0), P 1(0, y 1), and P 2(h, y 2), we have: y 0 = A(– h)2 + B(- h) + C = Ah 2 – Bh + C y 1 = C y 2 = Ah 2 + Bh + C

APPROXIMATE INTEGRATION Therefore, y 0 + 4 y 1 + y 2 = 2 Ah 2 + 6 C So, we can rewrite the area under the parabola as:

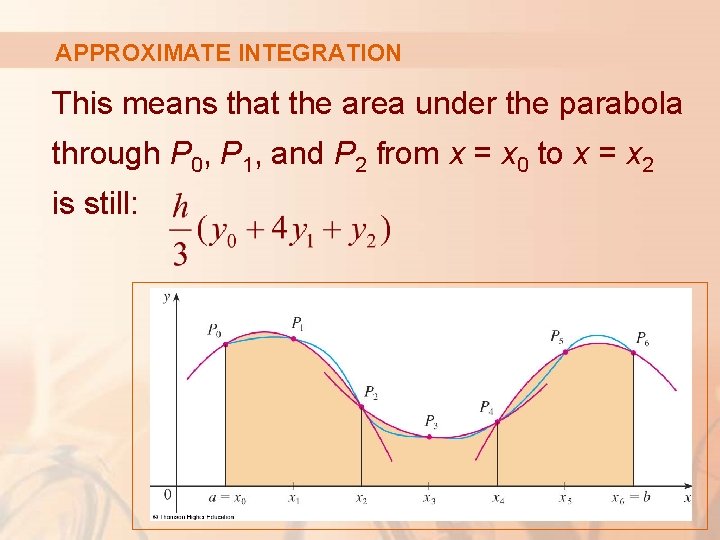
APPROXIMATE INTEGRATION Now, by shifting this parabola horizontally, we do not change the area under it.

APPROXIMATE INTEGRATION This means that the area under the parabola through P 0, P 1, and P 2 from x = x 0 to x = x 2 is still:

APPROXIMATE INTEGRATION Similarly, the area under the parabola through P 2, P 3, and P 4 from x = x 2 to x = x 4 is:

APPROXIMATE INTEGRATION Thus, if we compute the areas under all the parabolas and add the results, we get:

APPROXIMATE INTEGRATION Though we have derived this approximation for the case in which f(x) ≥ 0, it is a reasonable approximation for any continuous function f. § Note the pattern of coefficients: 1, 4, 2, . . . , 4, 2, 4, 1

SIMPSON’S RULE This is called Simpson’s Rule—after the English mathematician Thomas Simpson (1710– 1761).

SIMPSON’S RULE Rule where n is even and ∆x = (b – a)/n.
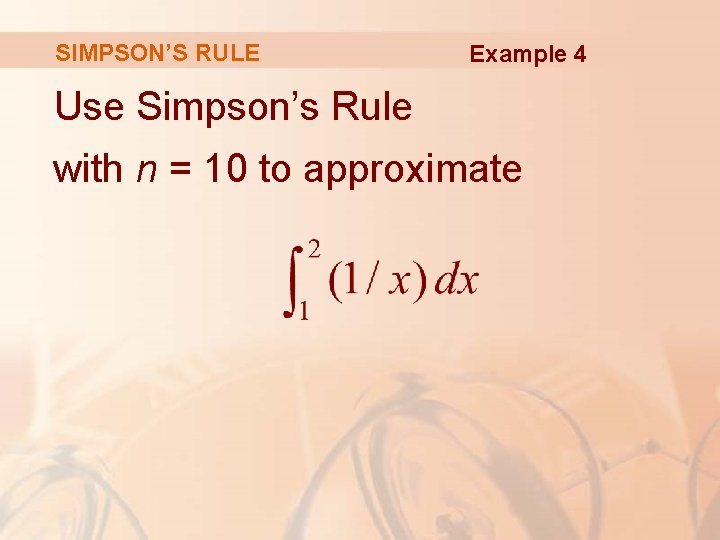
SIMPSON’S RULE Example 4 Use Simpson’s Rule with n = 10 to approximate

SIMPSON’S RULE Example 4 Putting f(x) = 1/x, n = 10, and ∆x = 0. 1 in Simpson’s Rule, we obtain:

SIMPSON’S RULE In Example 4, notice that Simpson’s Rule gives a much better approximation (S 10 ≈ 0. 693150) to the true value of the integral (ln 2 ≈ 0. 693147) than does either: § Trapezoidal Rule (T 10 ≈ 0. 693771) § Midpoint Rule (M 10 ≈ 0. 692835)

SIMPSON’S RULE It turns out that the approximations in Simpson’s Rule are weighted averages of those in the Trapezoidal and Midpoint Rules: § Recall that ET and EM usually have opposite signs and | EM | is about half the size of | ET |.

SIMPSON’S RULE In many applications of calculus, we need to evaluate an integral even if no explicit formula is known for y as a function of x. § A function may be given graphically or as a table of values of collected data.

SIMPSON’S RULE If there is evidence that the values are not changing rapidly, then the Trapezoidal Rule or Simpson’s Rule can still be used to find an approximate value for .

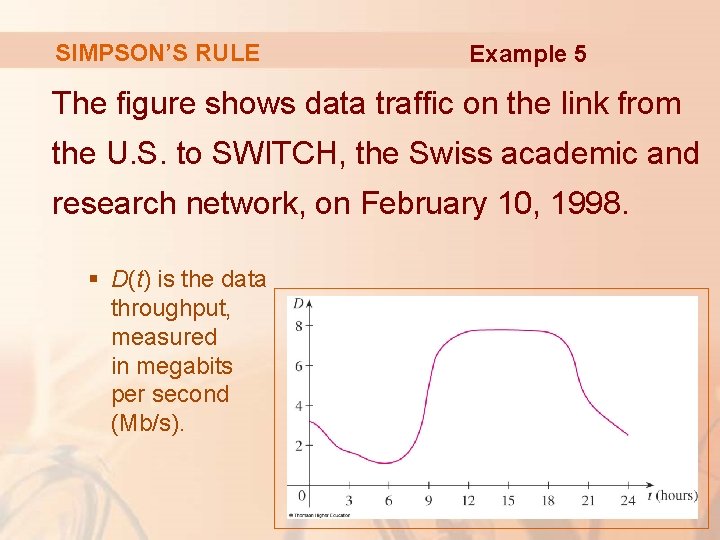
SIMPSON’S RULE Example 5 The figure shows data traffic on the link from the U. S. to SWITCH, the Swiss academic and research network, on February 10, 1998. § D(t) is the data throughput, measured in megabits per second (Mb/s).

SIMPSON’S RULE Example 5 Use Simpson’s Rule to estimate the total amount of data transmitted on the link up to noon on that day.

SIMPSON’S RULE Example 5 Since we want the units to be consistent and D(t) is measured in Mb/s, we convert the units for t from hours to seconds.

SIMPSON’S RULE Example 5 If we let A(t) be the amount of data (in Mb) transmitted by time t, where t is measured in seconds, then A’(t) = D(t). § So, by the Net Change Theorem (Section 5. 4), the total amount of data transmitted by noon (when t = 12 x 602 = 43, 200) is:

SIMPSON’S RULE Example 5 We estimate the values of D(t) at hourly intervals from the graph and compile them here.

SIMPSON’S RULE Example 5 Then, we use Simpson’s Rule with n = 12 and ∆t = 3600 to estimate the integral, as follows.

SIMPSON’S RULE Example 5 § The total amount of data transmitted up to noon is 144, 000 Mbs, or 144 gigabits.

SIMPSON’S RULE VS. MIDPOINT RULE The table shows how Simpson’s Rule compares with the Midpoint Rule for the integral is about 0. 69314718 , whose true value

SIMPSON’S RULE This table shows how the error Es in Simpson’s Rule decreases by a factor of about 16 when n is doubled.

SIMPSON’S RULE That is consistent with the appearance of n 4 in the denominator of the following error estimate for Simpson’s Rule. § It is similar to the estimates given in (3) for the Trapezoidal and Midpoint Rules. § However, it uses the fourth derivative of f.

ERROR BOUND (SIMPSON’S RULE) Estimate 4 Suppose that | f (4)(x) | ≤ K for a ≤ x ≤ b. If Es is the error involved in using Simpson’s Rule, then

ERROR BOUND (SIMPSON’S RULE) Example 6 How large should we take n to guarantee that the Simpson’s Rule approximation for is accurate to within 0. 0001?

ERROR BOUND (SIMPSON’S RULE) Example 6 If f(x) = 1/x, then f (4)(x) = 24/x 5. Since x ≥ 1, we have 1/x ≤ 1, and so § Thus, we can take K = 24 in (4).

ERROR BOUND (SIMPSON’S RULE) Example 6 So, for an error less than 0. 0001, we should choose n so that: § This gives or

ERROR BOUND (SIMPSON’S RULE) Example 6 Therefore, n = 8 (n must be even) gives the desired accuracy. § Compare this with Example 2, where we obtained n = 41 for the Trapezoidal Rule and n = 29 for the Midpoint Rule.

ERROR BOUND (SIMPSON’S RULE) Example 7 a. Use Simpson’s Rule with n = 10 to approximate the integral b. Estimate the error involved in this approximation. .

ERROR BOUND (SIMPSON’S RULE) Example 7 a If n =10, then ∆x = 0. 1 and the rule gives:
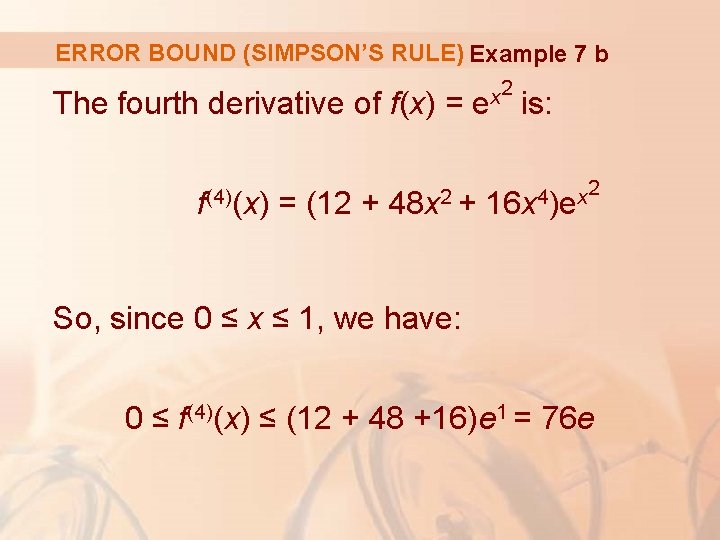
ERROR BOUND (SIMPSON’S RULE) Example 7 b The fourth derivative of f(x) = f(4)(x) = (12 + 2 x e 48 x 2 + is: 2 4 x 16 x )e So, since 0 ≤ x ≤ 1, we have: 0 ≤ f(4)(x) ≤ (12 + 48 +16)e 1 = 76 e

ERROR BOUND (SIMPSON’S RULE) Example 7 b Putting K = 76 e, a = 0, b = 1, and n = 10 in (4), we see that the error is at most: § Compare this with Example 3.

ERROR BOUND (SIMPSON’S RULE) Example 7 b Thus, correct to three decimal places, we have:
 Three dimensions of corporate strategy
Three dimensions of corporate strategy Forward integration and backward integration
Forward integration and backward integration Simultaneous integration and sequential integration
Simultaneous integration and sequential integration There is there are ejemplos
There is there are ejemplos What part of speech is open
What part of speech is open There is there are negative form
There is there are negative form There are there is
There are there is Some any cheese
Some any cheese There is there are
There is there are There fifteen candies in that bag. now there only one left
There fifteen candies in that bag. now there only one left Adjetivos demonstrativos
Adjetivos demonstrativos Some any farkı
Some any farkı Sustantivos en ingles contables
Sustantivos en ingles contables Pep unit
Pep unit There was there were ile ilgili cümleler
There was there were ile ilgili cümleler Negetive sentences
Negetive sentences There is there are
There is there are Arehay
Arehay There's and there are
There's and there are Ecological succession
Ecological succession Rules of integrals
Rules of integrals 7 techniques of integration
7 techniques of integration Chapter 7 techniques of integration
Chapter 7 techniques of integration Techniques of integration
Techniques of integration Fonctions techniques
Fonctions techniques Integrated quotes examples
Integrated quotes examples Integration symbol copy
Integration symbol copy Sitecore content hub integration
Sitecore content hub integration Voice data integration
Voice data integration Did vanderbilt use vertical integration
Did vanderbilt use vertical integration Docmail access dimensions integration
Docmail access dimensions integration Marketo microsoft dynamics crm integration
Marketo microsoft dynamics crm integration Trapezoidal rule
Trapezoidal rule Information oriented application integration
Information oriented application integration Information-oriented examples
Information-oriented examples Trapezoid rule
Trapezoid rule Technology integration planning model example
Technology integration planning model example Vertikale integration
Vertikale integration Vehicle infrastructure integration
Vehicle infrastructure integration Multi channel integration process
Multi channel integration process The rise
The rise Principle of integration
Principle of integration System integration life cycle
System integration life cycle Webmetrics statistics
Webmetrics statistics Area under the curve integration
Area under the curve integration Bernoulli brothers
Bernoulli brothers Tdc systems integration
Tdc systems integration Walmart horizontal integration
Walmart horizontal integration Transnational strategy vs global strategy
Transnational strategy vs global strategy Multisensory integration examples
Multisensory integration examples System integration testing checklist
System integration testing checklist Systems integration plan
Systems integration plan Msi medium scale integration
Msi medium scale integration Metapack microsoft dynamics nav integration
Metapack microsoft dynamics nav integration Medial and lateral apertures
Medial and lateral apertures Integrated quotation
Integrated quotation Sap b1if
Sap b1if Salesforce moodle integration
Salesforce moodle integration Communicator saleslogix integration
Communicator saleslogix integration Disadvantages of regional integration
Disadvantages of regional integration Enterprise integration reference architecture
Enterprise integration reference architecture Reentry and integration division
Reentry and integration division Multiplekser dan demultiplekser
Multiplekser dan demultiplekser Quote integration mla
Quote integration mla Integrated quotes examples
Integrated quotes examples Block quotation example
Block quotation example Passage writing in english
Passage writing in english Tangent skim integration
Tangent skim integration Unit impluse
Unit impluse Integration management in project management
Integration management in project management Project integration management diagram
Project integration management diagram Progress rollbase
Progress rollbase Excel numerical integration
Excel numerical integration Integration center
Integration center Pritchett merger integration
Pritchett merger integration Post merger integration training
Post merger integration training Orchastrate
Orchastrate Desegregation vs integration
Desegregation vs integration Docmail microsoft dynamics nav integration
Docmail microsoft dynamics nav integration Sap oracle integration
Sap oracle integration Opc ua device integration
Opc ua device integration National integration center functions
National integration center functions Discourse integration in nlp
Discourse integration in nlp Cyk meaning
Cyk meaning Product rule integrals
Product rule integrals Moodle fga
Moodle fga Mid market und enterprise
Mid market und enterprise Maximo enterprise services
Maximo enterprise services Ait assembly integration and test
Ait assembly integration and test Horizontal integration advantages
Horizontal integration advantages Market integration
Market integration Logarithmic exponential and other transcendental functions
Logarithmic exponential and other transcendental functions Integration by parts formula
Integration by parts formula Leibniz rule in integration
Leibniz rule in integration Different types of economic integration
Different types of economic integration Diversification de confortement
Diversification de confortement Jollibee horizontal integration
Jollibee horizontal integration Jcids
Jcids Dynatrace jira integration
Dynatrace jira integration Cruise control integration
Cruise control integration Downstream free riding
Downstream free riding Presentation integration model
Presentation integration model Multisensory integration
Multisensory integration