More on Derivatives and Integrals Product Rule Chain















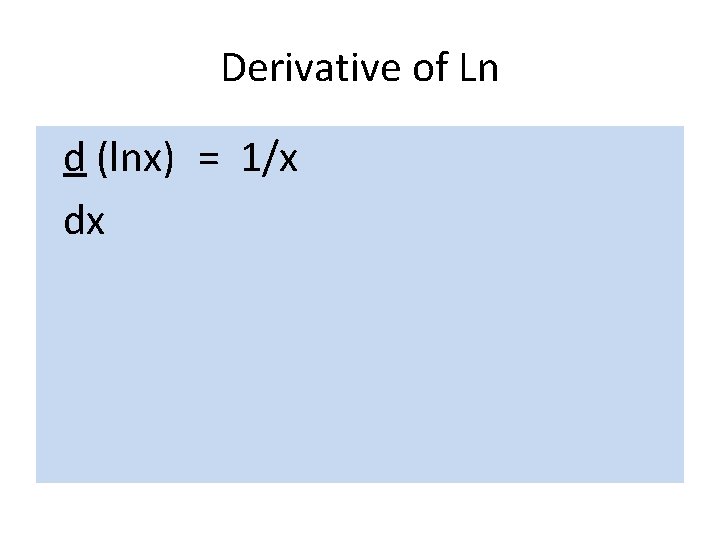

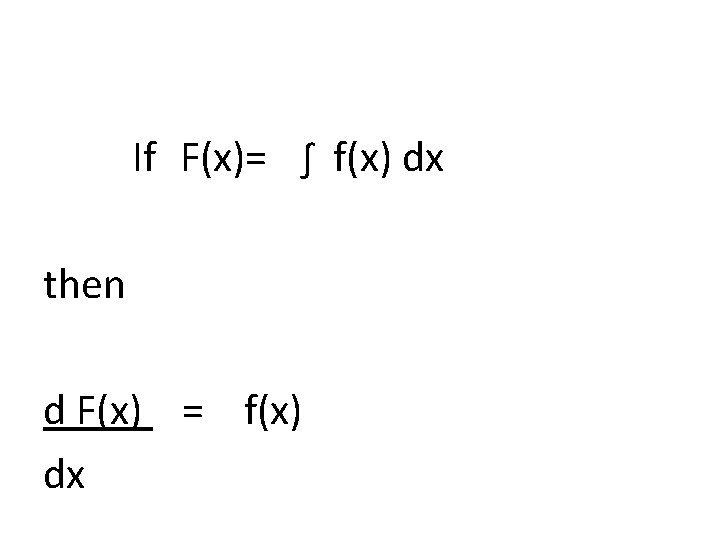






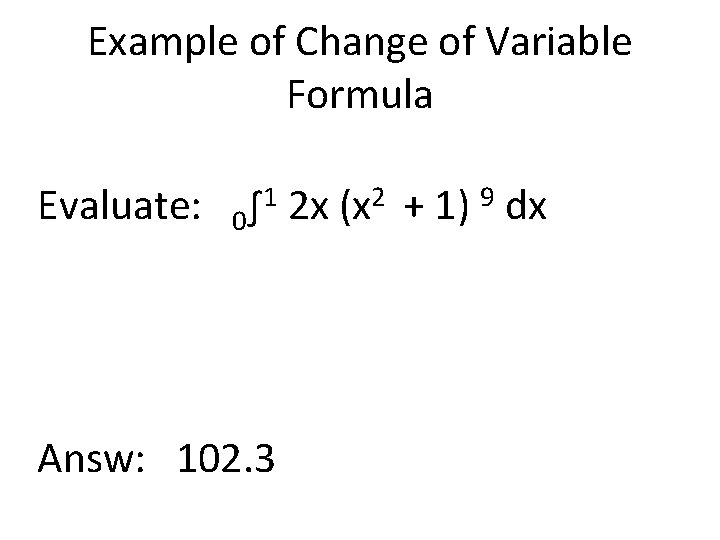



- Slides: 28

More on Derivatives and Integrals -Product Rule -Chain Rule AP Physics C Mrs. Coyle

Derivative f’ (x) = lim h 0 f(x + h) - f(x ) h

Derivative Notations f’ (x) . f df (x) dx df dx

Notations when evaluating the derivative at x=a f(a) f’(a) df (a) dx df |x=a dx

Basic Derivatives d(c) = 0 d(mx+b) = m dx dx d(x dx x≠ 0 n) =nx n-1 n is any integer

Derivative of a polynomial. For y(x) = axn dy = a n xn-1 dx -Apply to each term of the polynomial. -Note that the derivative of constant is 0.

Product Rule For two functions of x: u(x) and v (x) d [u(x) v (x)] =u d v (x) + v d u (x) dx dx dx or (uv)’ = u v’ + vu’

Example of Product Rule: Differentiate: F=(3 x-2)(x 2 + 5 x + 1) Answer: F’(x) = 9 x 2 + 26 x-7

Chain Rule If y=f(u) and u=g(x): dy = dy du dx

Example of Chain Rule Differentiate: F(x)= (x + 1) 2 Ans: F’(x)= 6(x 2 +1)2 x 3

Second Derivative Notations ’ df (x) dx 2 df d x 2 f’’(x)

Example of Second Derivative Compute the second derivative of y=(x)1/2 Ans: (-1/4) x-3/2

Derivatives of Trig Functions d sinx = cosx dx d tanx = sec 2 x dx d cosx = -sinx dx d secx = secx tanx dx

Derivative of the Exponential Function de dx u = e u du dx

Example of derivative of Exponential Function 2 Differentiate: 2 Ans: 2 x e x
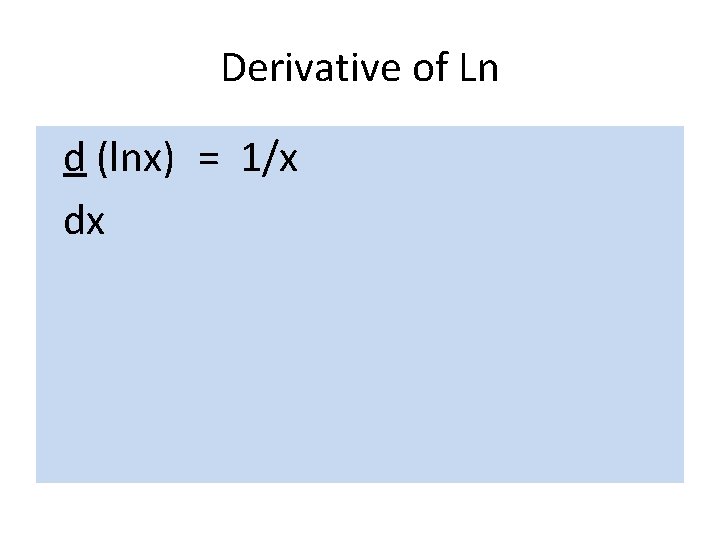
Derivative of Ln d (lnx) = 1/x dx

Definite Integral a b ∫ b f(x) dx= F(b)-F(a)= F(x)|a a and b are the limits of integration.
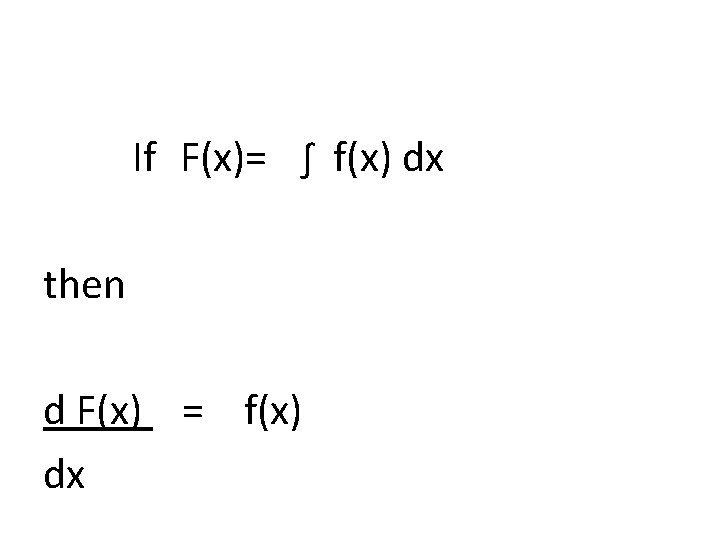
If F(x)= ∫ f(x) dx then d F(x) = f(x) dx

Properties of Integrals b cf(x) dx =c ∫b f(x) dx ∫ a a c f(x) dx = ∫b f(x) dx+ ∫c f(x) dx ∫ a a b a<b<c b (f(x)+g(x)) dx = ∫b f(x) dx+ ∫b g(x) dx ∫ a a a

Basic Integrals (integration constant ommited) ∫ xn dx = 1 xn+1 , n ≠ 1 n+1 ∫ ex dx = ex ∫ (1/x) dx = ln|x| ∫ cosx dx = sinx ∫ sinx dx = -cosx ∫ (1/x) dx = ln|x|

Example with computing work. • There is a force of 5 x 2 –x +2 N pulling on an object. Compute the work done in moving it from x=1 m to x=4 m. • Ans: 103. 5 N

To evaluate integrals of products of functions : • Chain Rule • Integration by parts • Change of Variable Formula

Change of Variable Formula When a function and its derivative appear in the integral: a b ∫ f[g(x)]g’(x) dx = g(a) g(b) ∫ f(y) dy

Example: When a function and its derivative appear in the integral: • Compute • Ans: 3. 75 x=1 2 x (x 2 +1) 3 dx ∫ x=0
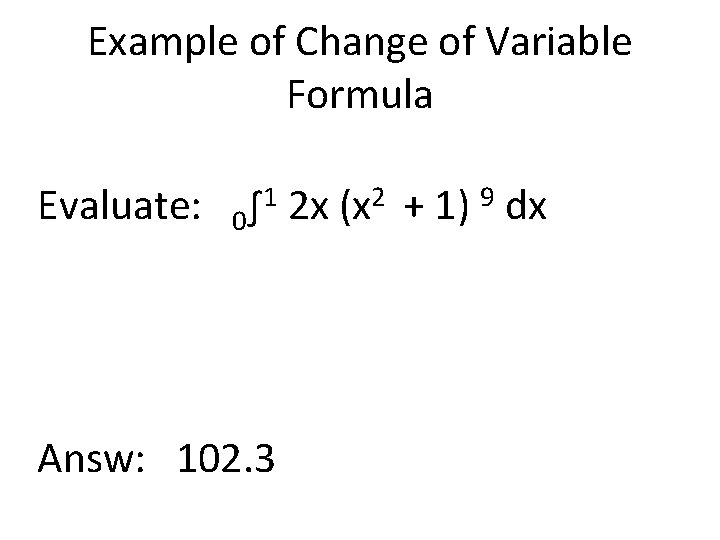
Example of Change of Variable Formula Evaluate: 1 2 x (x 2 + 1) 9 dx ∫ 0 Answ: 102. 3

Integration by Parts a b ∫ u(x) dv dx= dx b = u(x) v(x)|a - b v(x) du dx ∫ a dx

Integration by Parts a b ∫ b u v’ dx= u v|a - a b ∫ v u’ dx

Example of Integration by Parts Compute Ans: π π x sinx dx ∫ 0
 More more more i want more more more more we praise you
More more more i want more more more more we praise you More more more i want more more more more we praise you
More more more i want more more more more we praise you Chain rule integrals
Chain rule integrals Chain rule integrals
Chain rule integrals Product rule of integration
Product rule of integration Integral ln x dx
Integral ln x dx Product rule
Product rule Contoh soal turunan fungsi aturan rantai
Contoh soal turunan fungsi aturan rantai Derivative of composite function
Derivative of composite function Chain rule examples
Chain rule examples Substitution rule
Substitution rule Product and quotient rules and higher order derivatives
Product and quotient rules and higher order derivatives Product rule for counting
Product rule for counting Food chain sequence
Food chain sequence Chain rule power rule
Chain rule power rule Differentiation of constant
Differentiation of constant Derivative exponential function rule
Derivative exponential function rule Duality theorem in antenna
Duality theorem in antenna Fourier series and integrals
Fourier series and integrals Integrals involving powers of secant and tangent
Integrals involving powers of secant and tangent Average rate of change with integrals
Average rate of change with integrals Riemann sum sigma notation calculator
Riemann sum sigma notation calculator Convolution integral example
Convolution integral example Trigonemtric integrals
Trigonemtric integrals Net change theorem
Net change theorem Properties of indefinite integrals
Properties of indefinite integrals Signals and systems
Signals and systems Easy integrals
Easy integrals Contoh soal integral permukaan
Contoh soal integral permukaan