7 TECHNIQUES OF INTEGRATION TECHNIQUES OF INTEGRATION 7






















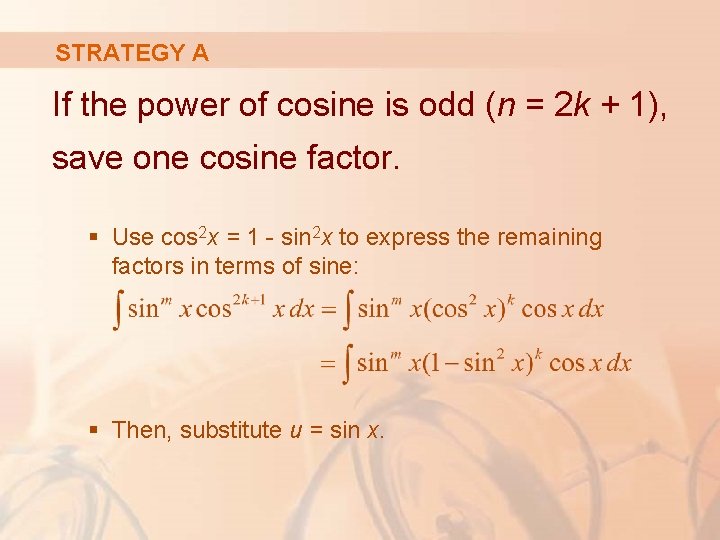
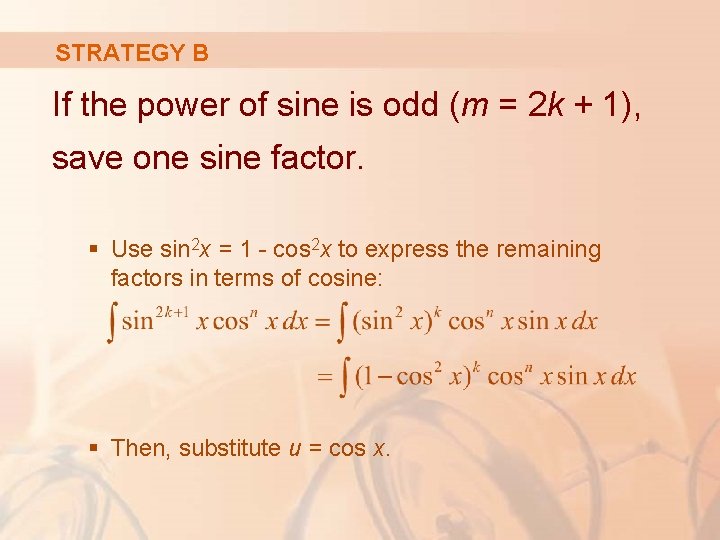



















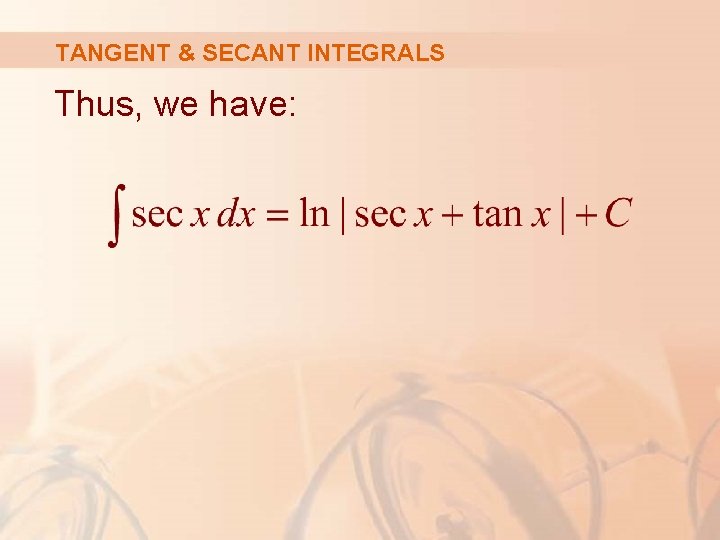











- Slides: 56

7 TECHNIQUES OF INTEGRATION

TECHNIQUES OF INTEGRATION 7. 2 Trigonometric Integrals In this section, we will learn: How to use trigonometric identities to integrate certain combinations of trigonometric functions.

TRIGONOMETRIC INTEGRALS We start with powers of sine and cosine.

SINE & COSINE INTEGRALS Example 1 Evaluate ∫ cos 3 x dx § Simply substituting u = cos x isn’t helpful, since then du = -sin x dx. § In order to integrate powers of cosine, we would need an extra sin x factor. § Similarly, a power of sine would require an extra cos x factor.

SINE & COSINE INTEGRALS Example 1 Thus, here we can separate one cosine factor and convert the remaining cos 2 x factor to an expression involving sine using the identity sin 2 x + cos 2 x = 1: cos 3 x = cos 2 x. cosx = (1 - sin 2 x) cosx

SINE & COSINE INTEGRALS Example 1 We can then evaluate the integral by substituting u = sin x. So, du = cos x dx and

SINE & COSINE INTEGRALS In general, we try to write an integrand involving powers of sine and cosine in a form where we have only one sine factor. § The remainder of the expression can be in terms of cosine.

SINE & COSINE INTEGRALS We could also try only one cosine factor. § The remainder of the expression can be in terms of sine.

SINE & COSINE INTEGRALS The identity sin 2 x + cos 2 x = 1 enables us to convert back and forth between even powers of sine and cosine.

SINE & COSINE INTEGRALS Example 2 Find ∫ sin 5 x cos 2 x dx § We could convert cos 2 x to 1 – sin 2 x. § However, we would be left with an expression in terms of sin x with no extra cos x factor.

SINE & COSINE INTEGRALS Example 2 Instead, we separate a single sine factor and rewrite the remaining sin 4 x factor in terms of cos x. So, we have:

SINE & COSINE INTEGRALS Example 2 Substituting u = cos x, we have du = sin x dx. So,

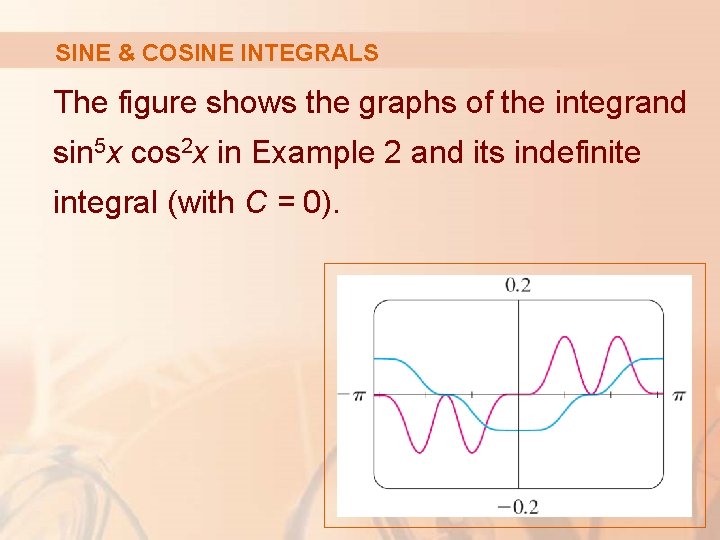
SINE & COSINE INTEGRALS The figure shows the graphs of the integrand sin 5 x cos 2 x in Example 2 and its indefinite integral (with C = 0).

SINE & COSINE INTEGRALS In the preceding examples, an odd power of sine or cosine enabled us to separate a single factor and convert the remaining even power. § If the integrand contains even powers of both sine and cosine, this strategy fails.

SINE & COSINE INTEGRALS In that case, we can take advantage of the following half-angle identities:

SINE & COSINE INTEGRALS Example 3 Evaluate § If we write sin 2 x = 1 - cos 2 x, the integral is no simpler to evaluate.

SINE & COSINE INTEGRALS Example 3 However, using the half-angle formula for sin 2 x, we have:

SINE & COSINE INTEGRALS Example 3 Notice that we mentally made the substitution u = 2 x when integrating cos 2 x. § Another method for evaluating this integral was given in Exercise 43 in Section 7. 1

SINE & COSINE INTEGRALS Example 4 Find ∫ sin 4 x dx § We could evaluate this integral using the reduction formula for ∫ sinnx dx (Equation 7 in Section 7. 1) together with Example 3.

SINE & COSINE INTEGRALS Example 4 However, a better method is to write and use a half-angle formula:

SINE & COSINE INTEGRALS Example 4 As cos 2 2 x occurs, we must use another half-angle formula:

SINE & COSINE INTEGRALS This gives: Example 4

SINE & COSINE INTEGRALS To summarize, we list guidelines to follow when evaluating integrals of the form ∫ sinmx cosnx dx where m ≥ 0 and n ≥ 0 are integers.
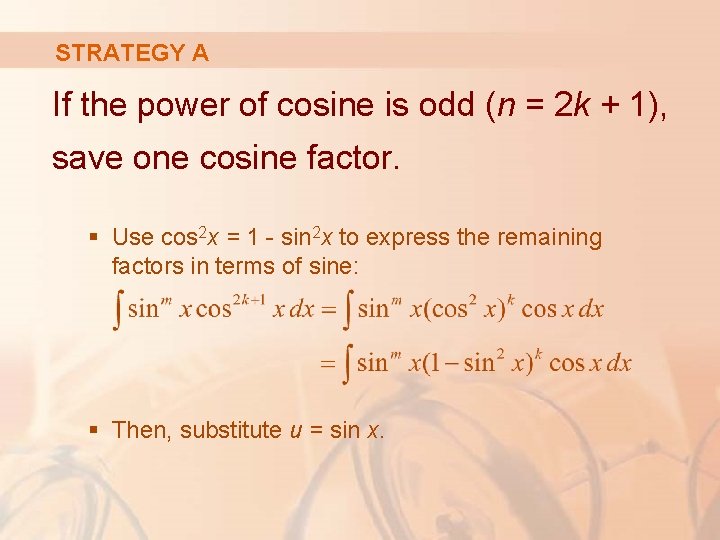
STRATEGY A If the power of cosine is odd (n = 2 k + 1), save one cosine factor. § Use cos 2 x = 1 - sin 2 x to express the remaining factors in terms of sine: § Then, substitute u = sin x.
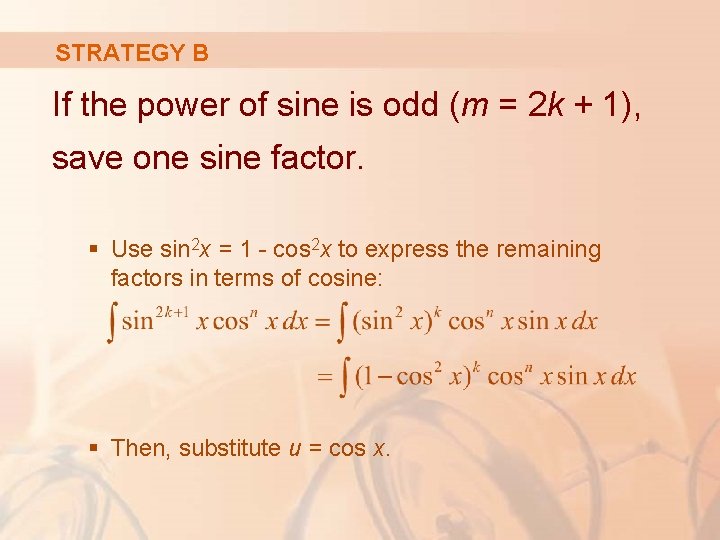
STRATEGY B If the power of sine is odd (m = 2 k + 1), save one sine factor. § Use sin 2 x = 1 - cos 2 x to express the remaining factors in terms of cosine: § Then, substitute u = cos x.

STRATEGIES Note that, if the powers of both sine and cosine are odd, either (A) or (B) can be used.

STRATEGY C If the powers of both sine and cosine are even, use the half-angle identities § Sometimes, it is helpful to use the identity

TANGENT & SECANT INTEGRALS We can use a similar strategy to evaluate integrals of the form ∫ tanmx secnx dx

TANGENT & SECANT INTEGRALS As (d/dx)tan x = sec 2 x, we can separate a sec 2 x factor. § Then, we convert the remaining (even) power of secant to an expression involving tangent using the identity sec 2 x = 1 + tan 2 x.

TANGENT & SECANT INTEGRALS Alternately, as (d/dx) sec x = sec x tan x, we can separate a sec x tan x factor and convert the remaining (even) power of tangent to secant.

TANGENT & SECANT INTEGRALS Example 5 Evaluate ∫ tan 6 x sec 4 x dx § If we separate one sec 2 x factor, we can express the remaining sec 2 x factor in terms of tangent using the identity sec 2 x = 1 + tan 2 x. § Then, we can evaluate the integral by substituting u = tan x so that du = sec 2 x dx.

TANGENT & SECANT INTEGRALS Example 5 We have:

TANGENT & SECANT INTEGRALS Example 6 Find ∫ tan 5 θ sec 7θ § If we separate a sec 2θ factor, as in the preceding example, we are left with a sec 5θ factor. § This isn’t easily converted to tangent.

TANGENT & SECANT INTEGRALS Example 6 However, if we separate a sec θ tan θ factor, we can convert the remaining power of tangent to an expression involving only secant. § We can use the identity tan 2θ = sec 2θ – 1.

TANGENT & SECANT INTEGRALS Example 6 We can then evaluate the integral by substituting u = sec θ, so du = sec θ tan θ dθ:

TANGENT & SECANT INTEGRALS The preceding examples demonstrategies for evaluating integrals in the form ∫ tanmx secnx for two cases—which we summarize here.

STRATEGY A If the power of secant is even (n = 2 k, k ≥ 2) save sec 2 x. § Then, use tan 2 x = 1 + sec 2 x to express the remaining factors in terms of tan x: § Then, substitute u = tan x.

STRATEGY B If the power of tangent is odd (m = 2 k + 1), save sec x tan x. § Then, use tan 2 x = sec 2 x – 1 to express the remaining factors in terms of sec x: § Then, substitute u = sec x.

OTHER INTEGRALS For other cases, the guidelines are not as clear-cut. We may need to use: § Identities § Integration by parts § A little ingenuity

TANGENT & SECANT INTEGRALS We will need to be able to integrate tan x by using Formula 5 from Section 5. 5 :

TANGENT & SECANT INTEGRALS Formula 1 We will also need the indefinite integral of secant:

TANGENT & SECANT INTEGRALS We could verify Formula 1 by differentiating the right side, or as follows.

TANGENT & SECANT INTEGRALS First, we multiply numerator and denominator by sec x + tan x:

TANGENT & SECANT INTEGRALS If we substitute u = sec x + tan x, then du = (sec x tan x + sec 2 x). § The integral becomes: ∫ (1/u) du = ln |u| + C
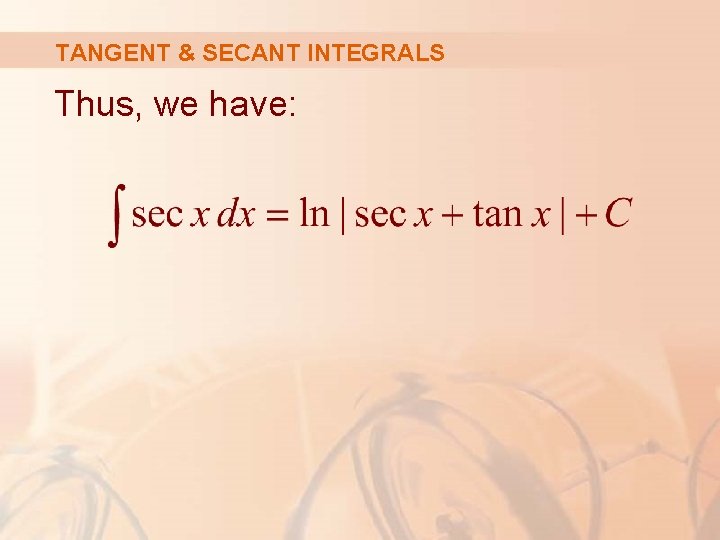
TANGENT & SECANT INTEGRALS Thus, we have:

TANGENT & SECANT INTEGRALS Example 7 Find ∫ tan 3 x dx § Here, only tan x occurs. § So, we rewrite a tan 2 x factor in terms of sec 2 x.

TANGENT & SECANT INTEGRALS Example 7 Hence, we use tan 2 x - sec 2 x = 1. § In the first integral, we mentally substituted u = tan x so that du = sec 2 x dx.

TANGENT & SECANT INTEGRALS If an even power of tangent appears with an odd power of secant, it is helpful to express the integrand completely in terms of sec x. § Powers of sec x may require integration by parts, as shown in the following example.

TANGENT & SECANT INTEGRALS Example 8 Find ∫ sec 3 x dx § Here, we integrate by parts with

TANGENT & SECANT INTEGRALS Example 8 Then,

TANGENT & SECANT INTEGRALS Example 8 Using Formula 1 and solving for the required integral, we get:

TANGENT & SECANT INTEGRALS Integrals such as the one in the example may seem very special. § However, they occur frequently in applications of integration. § We will see this in Chapter 8.

COTANGENT & COSECANT INTEGRALS Integrals of the form ∫ cotmx cscnx dx can be found by similar methods. § We have to make use of the identity 1 + cot 2 x = csc 2 x

OTHER INTEGRALS Finally, we can make use of another set of trigonometric identities, as follows.

OTHER INTEGRALS Equation 2 In order to evaluate the integral, use the corresponding identity. Integral a ∫ sin mx cos nx dx b ∫ sin mx sin nx dx c ∫ cos mx cos nx dx Identity

TRIGONOMETRIC INTEGRALS Example 9 Evaluate ∫ sin 4 x cos 5 x dx § This could be evaluated using integration by parts. § It’s easier to use the identity in Equation 2(a):
 Three dimensions of corporate strategy
Three dimensions of corporate strategy Forward and backward integration
Forward and backward integration Simultaneous integration
Simultaneous integration 7 techniques of integration
7 techniques of integration Chapter 7 techniques of integration
Chapter 7 techniques of integration Techniques of integration
Techniques of integration Basic rule of integration
Basic rule of integration Fonctions techniques
Fonctions techniques Vertical integration
Vertical integration Explain project integration management
Explain project integration management Types of economic integration pdf
Types of economic integration pdf Production integration
Production integration Integration and synthesis
Integration and synthesis Impact of integration
Impact of integration Démonstration marketo
Démonstration marketo Vertical integration
Vertical integration Interaction patterns in groups
Interaction patterns in groups Metapack microsoft dynamics nav integration
Metapack microsoft dynamics nav integration Vertical integration?
Vertical integration? Nvr pos integration
Nvr pos integration Synaptic integration
Synaptic integration Riva crm integration
Riva crm integration Regionalization and globalization venn diagram
Regionalization and globalization venn diagram Logarithmic exponential and other transcendental functions
Logarithmic exponential and other transcendental functions Chapter 17 nomadic empires and eurasian integration
Chapter 17 nomadic empires and eurasian integration Nexthink servicenow integration
Nexthink servicenow integration Webmetrics statistics
Webmetrics statistics 1500-1269
1500-1269 What are the challenges of adolescence
What are the challenges of adolescence Integration of power series
Integration of power series Infor xa
Infor xa Lipet rule
Lipet rule Soa reference architecture
Soa reference architecture Team foundation server office integration
Team foundation server office integration Product rule in integration
Product rule in integration Integral rules
Integral rules Data services framework
Data services framework Sugarcrm sage 1000 integration
Sugarcrm sage 1000 integration Integration point bonn
Integration point bonn Airflow ci/cd pipeline
Airflow ci/cd pipeline 3 part source integration
3 part source integration Horizontal integration strategies
Horizontal integration strategies Product rule integration
Product rule integration Technology integration planning model example
Technology integration planning model example Vertical integration
Vertical integration Kinästhetische reize
Kinästhetische reize Vertical integration
Vertical integration Dicom integration solutions
Dicom integration solutions Data mashups and gis are data integration technologies.
Data mashups and gis are data integration technologies. Post merger integration assessment
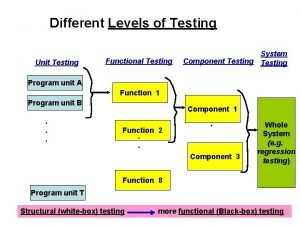
Post merger integration assessment Different levels of testing
Different levels of testing Derivative of inverse sine
Derivative of inverse sine Six processes of project integration management
Six processes of project integration management Final integration
Final integration Drupal 8 crm
Drupal 8 crm Desegregation vs integration
Desegregation vs integration Pneumatic switch symbol
Pneumatic switch symbol