4 5 FONCTION EXPONENTIELLE ET LOGARITHMIQUE cours 27





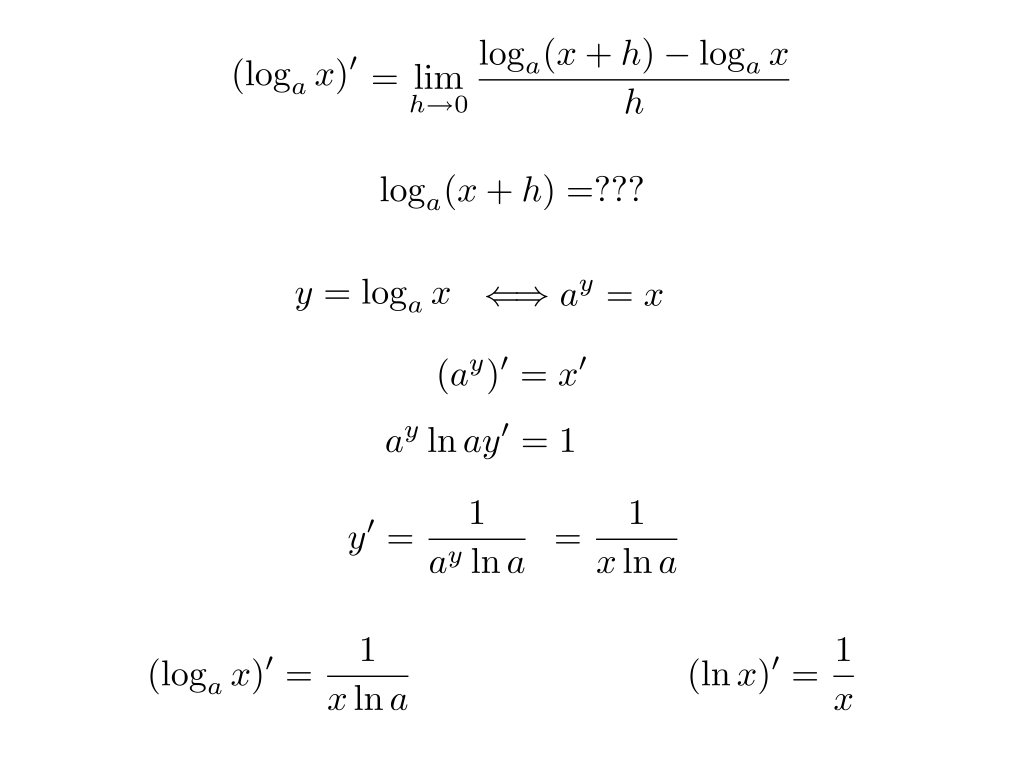




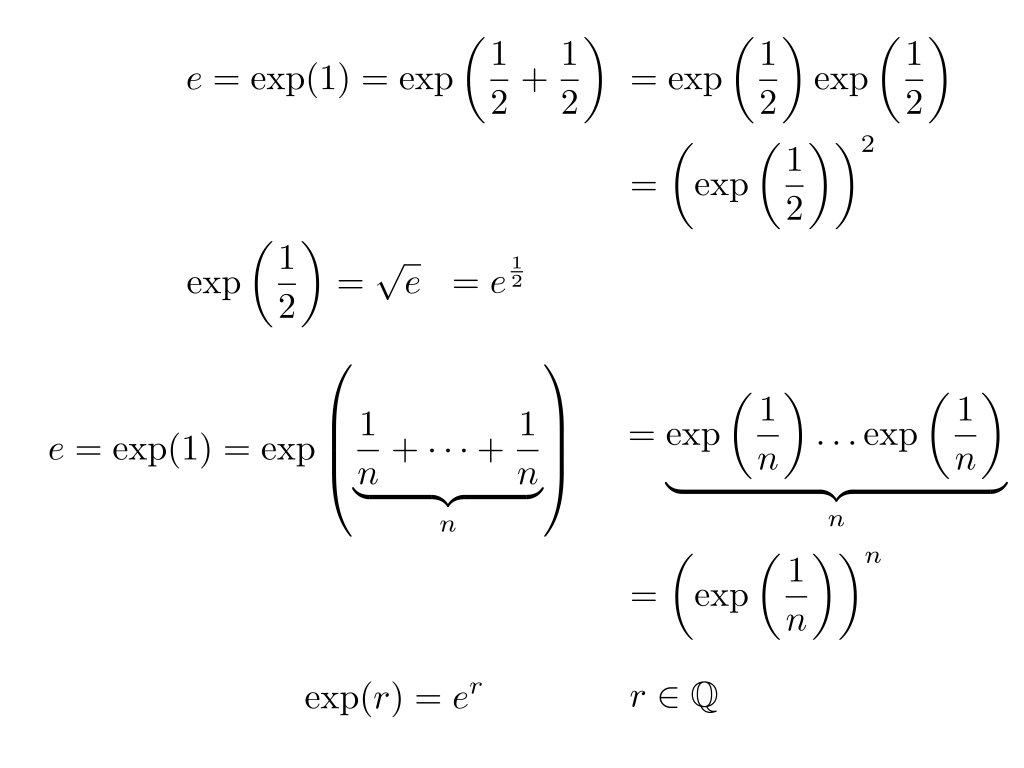

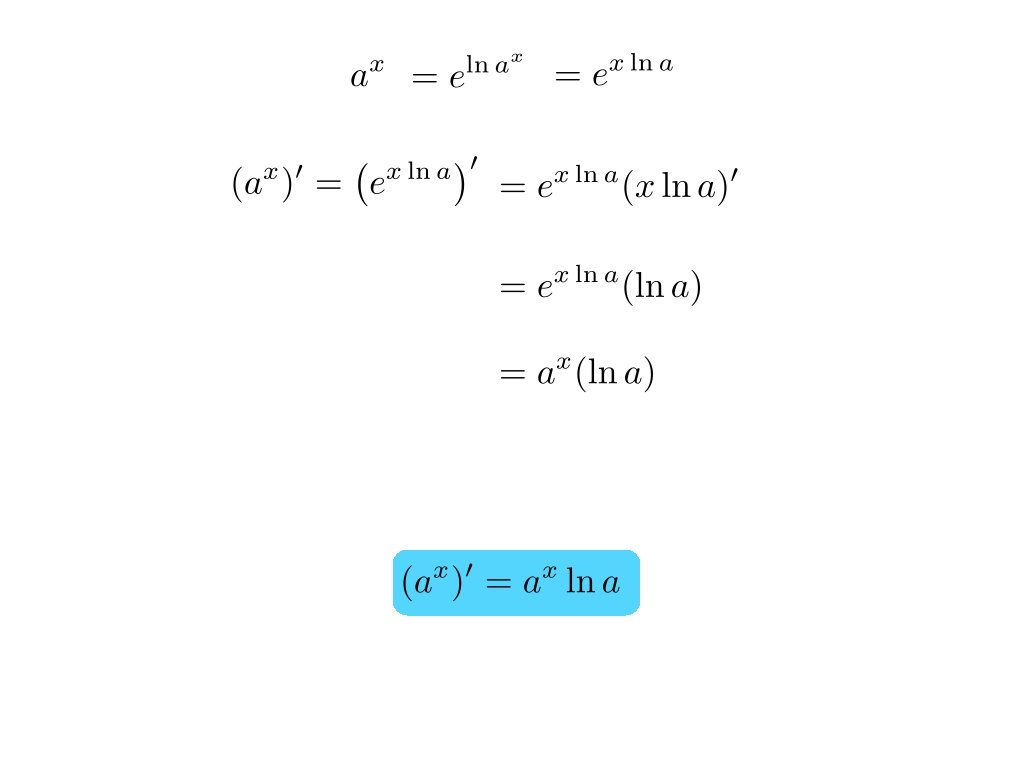







- Slides: 26

4. 5 FONCTION EXPONENTIELLE ET LOGARITHMIQUE cours 27

Au dernier cours, nous avons vu

Aujourd’hui, nous allons voir ✓ Dérivée des fonctions exponentielles et logarithmiques

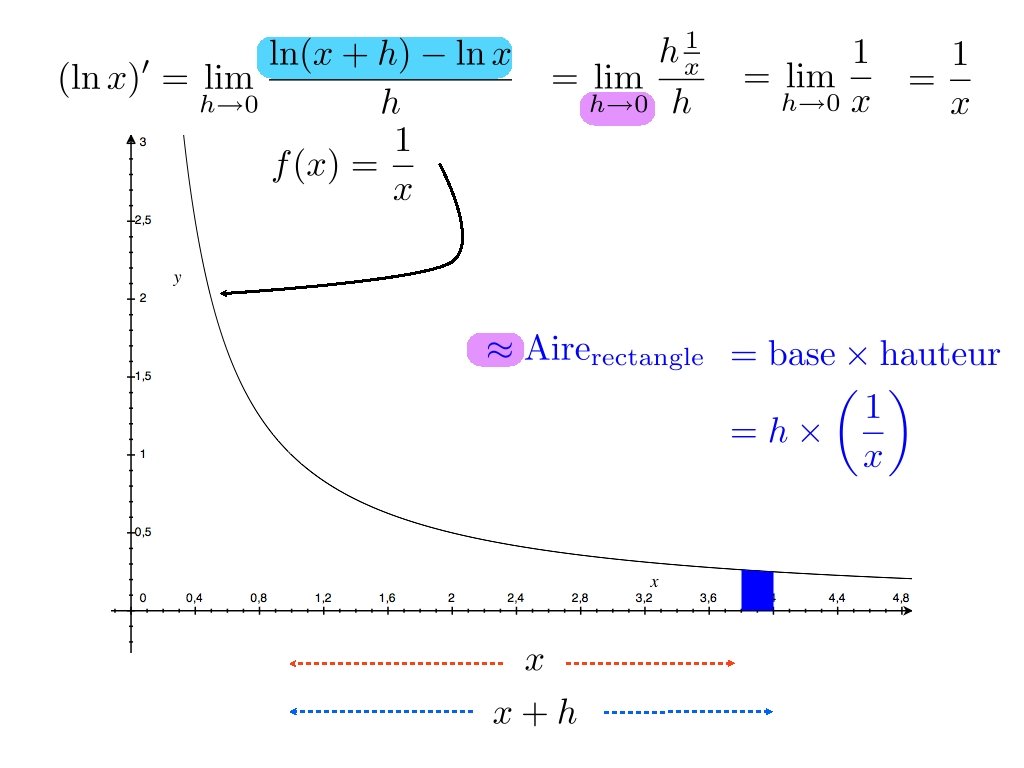
Calculons la dérivée de ces fonctions Si cette limite existe, c’est une constante. Reste à savoir ce que vaut cette limite.

Malheureusement, nous n’avons pas les outils pour évaluer cette limite Nous allons au moins tenter une approche numérique.

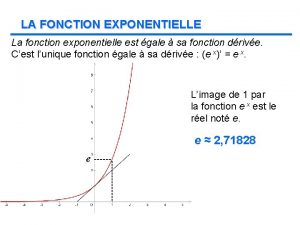
Naturellement cette démarche ne démontre absolument rien. Tout ce qu’elle fait est de laisser entendre que l’égalité suivante est peut-être vrai. Dans le cas particulier où la base est le nombre Exemple :
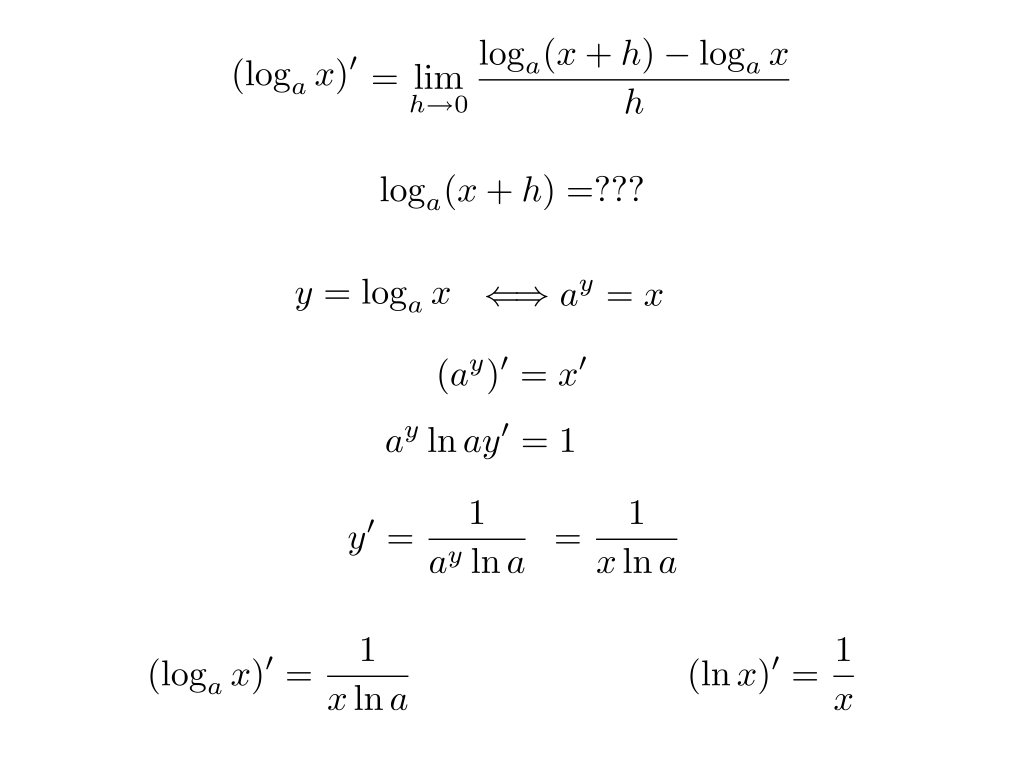

Approche alternative Historiquement les fonctions exponentielle et logarithmique ont été étudier indépendamment. On peut commencer par définir l’exponentielle et définir le logarithme comme sa fonction inverse. Ou bien on commence par définir le logarithme et on défini l’exponentielle comme sa fonction inverse.

Historiquement le logarithme est apparue pour transformer les produits en sommes.

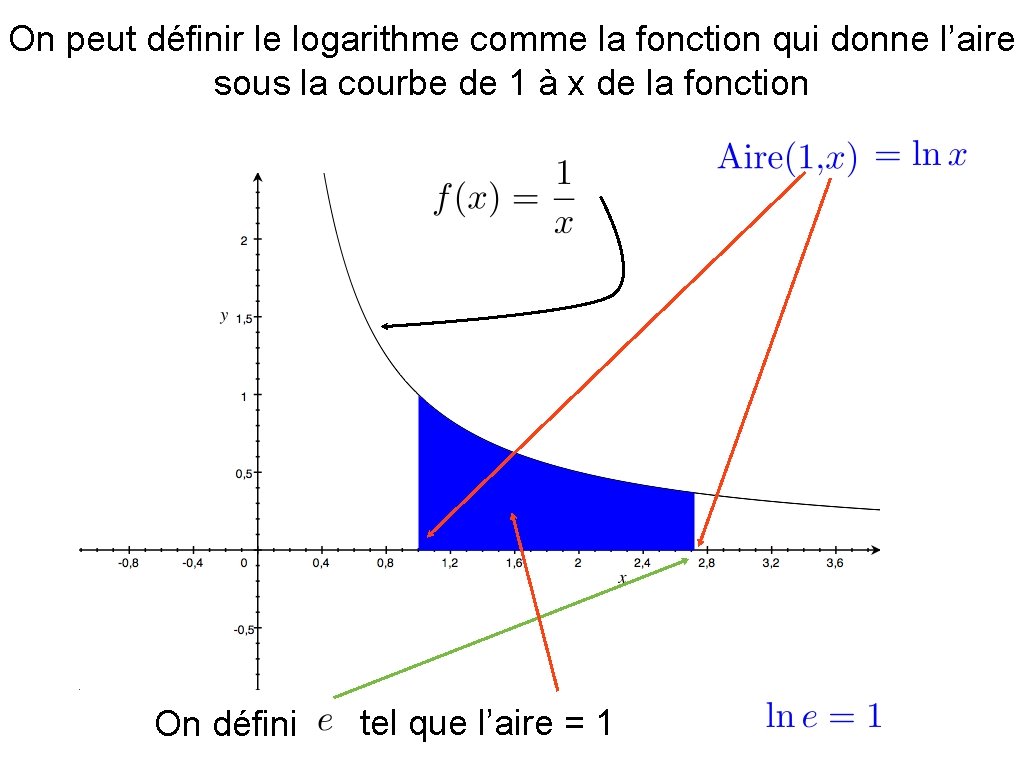
On peut définir le logarithme comme la fonction qui donne l’aire sous la courbe de 1 à x de la fonction On défini tel que l’aire = 1


À l’aide de cette dérivée, on trouve Si Si Donc la fonction qu’on a nommée ln possède bien la propriété voulue.

Essayons de comprendre la fonction réciproque. Par définition Car pour
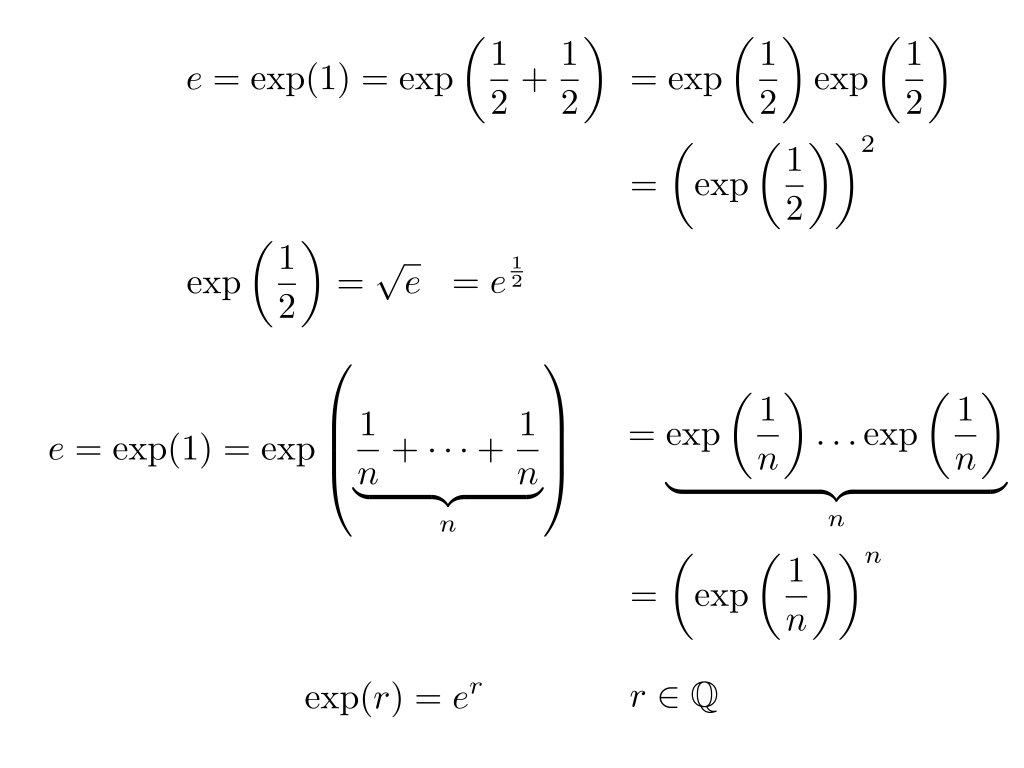

Donc on a bien que
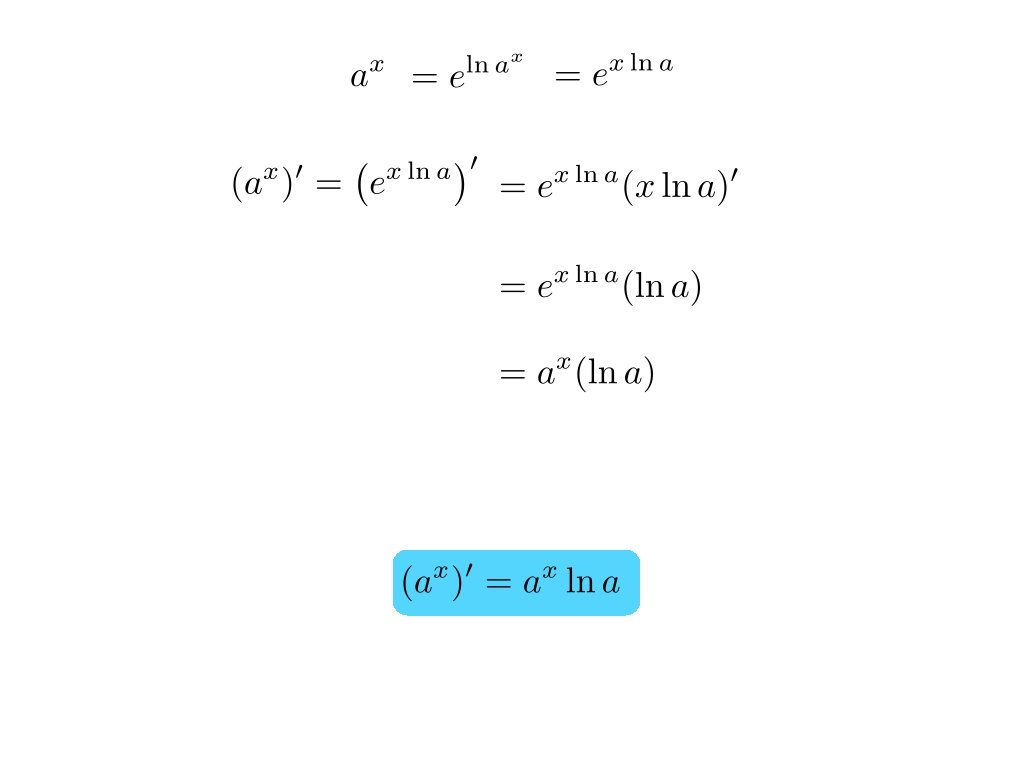

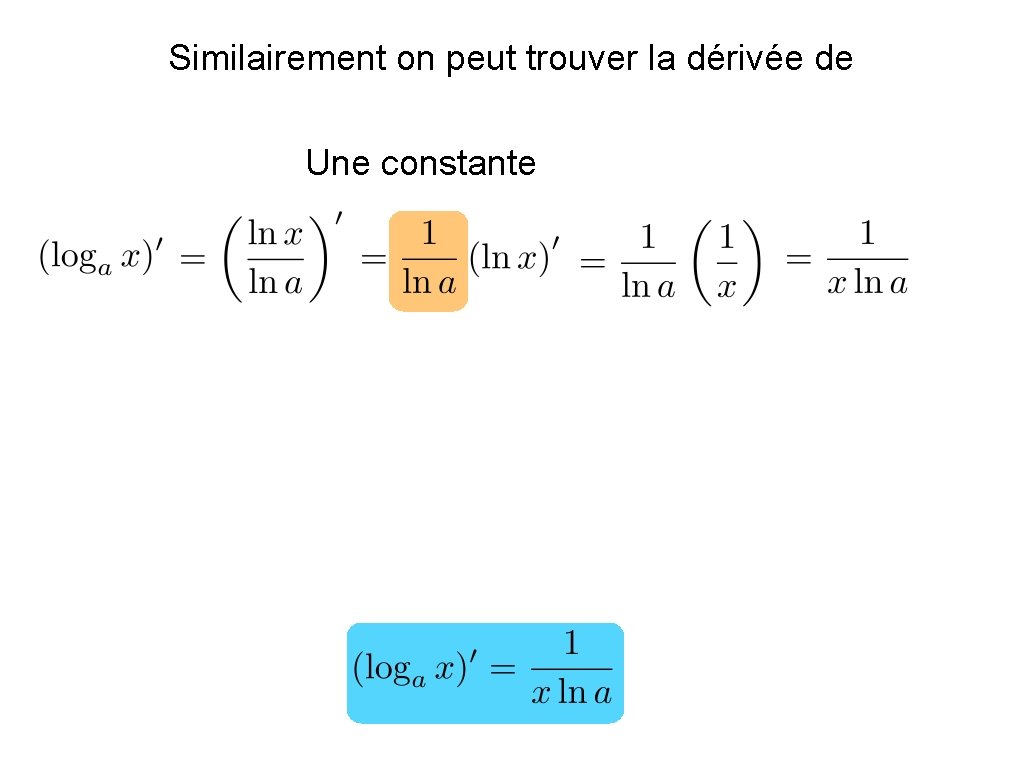
Similairement on peut trouver la dérivée de Une constante

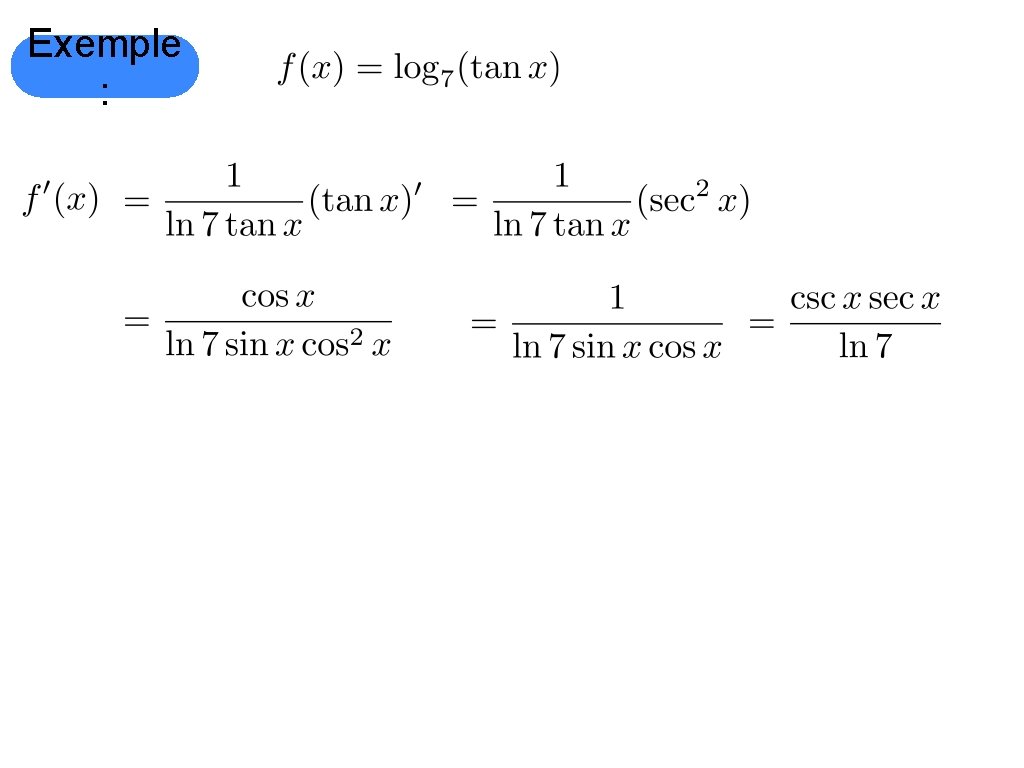
Exemple :

Faites les exercices suivants # 24 et 25

Exemple :

Exemple :

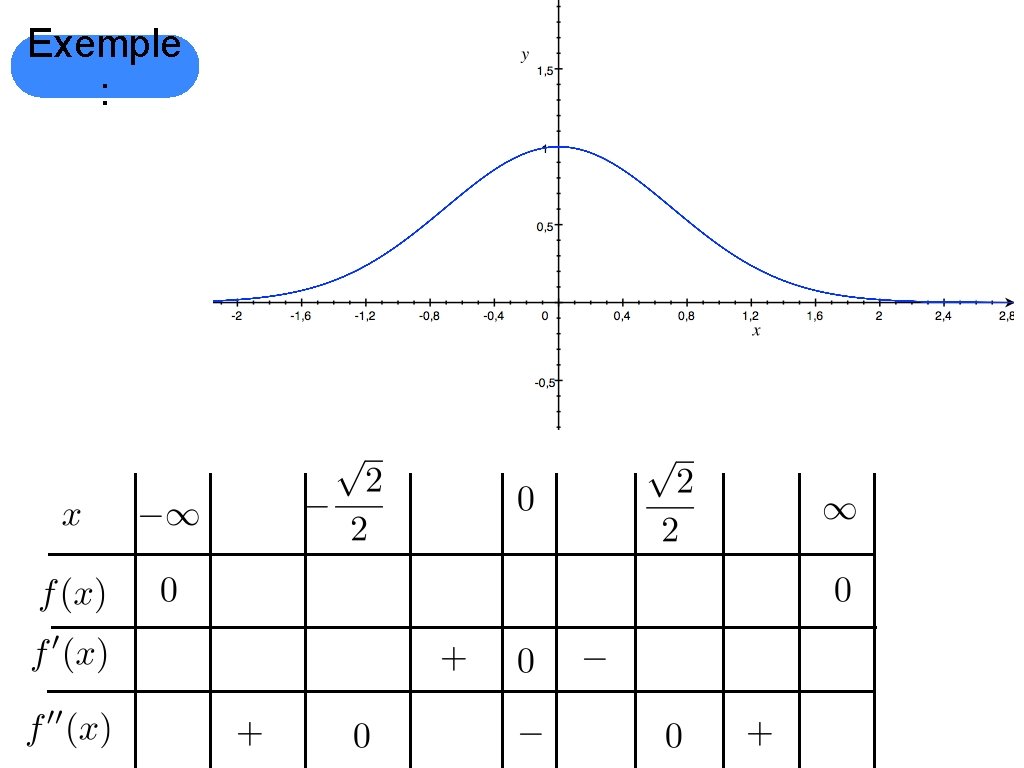
Exemple Faire l’analyse complète de : pt. cr. :

Exemple :

Faites les exercices suivants # 26

Aujourd’hui, nous avons vu

Devoir: #24 à 30
 Tangente fonction exponentielle
Tangente fonction exponentielle Fonction exponentielle st2s
Fonction exponentielle st2s Challenge test cosmétique critère a et b
Challenge test cosmétique critère a et b Propriété exponentielle
Propriété exponentielle Exponentielle glättung 2 ordnung excel
Exponentielle glättung 2 ordnung excel Rincarnation
Rincarnation Argsinh
Argsinh Fonction des articles
Fonction des articles Fonction partie entiere
Fonction partie entiere Fonction globale du chariot de lavage
Fonction globale du chariot de lavage Fonction logique
Fonction logique Architecture cirque romain
Architecture cirque romain Fonction alimenter
Fonction alimenter Dérivée de fonction rationnelle
Dérivée de fonction rationnelle Exercice matlab fonction
Exercice matlab fonction La fonction de transfert d'un filtre
La fonction de transfert d'un filtre Schéma à contact fonction logique
Schéma à contact fonction logique Differenciation verticale et horizontale des produits
Differenciation verticale et horizontale des produits Relais thermique tripolaire fonction
Relais thermique tripolaire fonction Contacteur fonction
Contacteur fonction La fonction expressive
La fonction expressive Fonctions techniques
Fonctions techniques Fonction technique scooter
Fonction technique scooter Fonction affine
Fonction affine Tchité expression
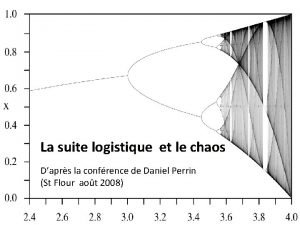
Tchité expression Fonction logistique chaos
Fonction logistique chaos Fonction dusage dun pont
Fonction dusage dun pont