www cs technion ac ilreuven Approximation Algorithms for

www. cs. technion. ac. il/~reuven Approximation Algorithms for Bandwidth and Storage Allocation Reuven Bar-Yehuda Joint work with Michael Beder, Yuval Cohen and Dror Rawitz Technion IIT Slides and paper at: http: //www. cs. technion. ac. il/~reuven 1

www. cs. technion. ac. il/~reuven The Local-Ratio Technique: Basic definitions Given a profit [penalty] vector p. Maximize[Minimize] p·x Subject to: feasibility constraints F(x) x is r-approximation if F(x) and p·x [ ] r · p·x* An algorithm is r-approximation if for any p, F it returns an r-approximation 2

www. cs. technion. ac. il/~reuven The Local-Ratio Theorem: x is an r-approximation with respect to p 1 x is an r-approximation with respect to p- p 1 x is an r-approximation with respect to p Proof: (For maximization) p 1 · x r × p 1* p 2 · x r × p 2* p · x r × ( p 1*+ p 2*) r × ( p 1 + p 2 )* 3

www. cs. technion. ac. il/~reuven Special case: Optimization is 1 -approximation x is an optimum with respect to p 1 x is an optimum with respect to p- p 1 x is an optimum with respect to p 4

A Local-Ratio Schema for Maximization[Minimization] problems: www. cs. technion. ac. il/~reuven 5 Algorithm r-Approx. Max[Min]( Set, p ) If Set = Φ then return Φ ; If I Set p(I) 0 then return r-Approx. Max( Set-{I}, p ) ; [If I Set p(I)=0 then return {I} r-Approx. Min( Set-{I}, p ) ; ] Define “good” p 1 ; REC = r-Approx. Max[Min]( S, p- p 1 ) ; If REC is not an r-approximation w. r. t. p 1 then “fix it”; return REC;

www. cs. technion. ac. il/~reuven The Local-Ratio Theorem: Applications to some optimization algorithms (r = 1): ( MST) Minimum Spanning Tree (Kruskal) ( SHORTEST-PATH) s-t Shortest Path (Dijkstra) (LONGEST-PATH) s-t DAG Longest Path (Can be done with dynamic programming) (INTERVAL-IS) Independents-Set in Interval Graphs Usually done with dynamic programming) (LONG-SEQ) Longest (weighted) monotone subsequence (Can be done with dynamic programming) ( MIN_CUT) Minimum Capacity s, t Cut (e. g. Ford, Dinitz) Applications to some 2 -Approximation algorithms: (r = 2) ( VC) Minimum Vertex Cover (Bar-Yehuda and Even) ( FVS) Vertex Feedback Set (Becker and Geiger) ( GSF) Generalized Steiner Forest (Williamson, Goemans, Mihail, and Vazirani) ( Min 2 SAT) Minimum Two-Satisfibility (Gusfield and Pitt) ( 2 VIP) Two Variable Integer Programming (Bar-Yehuda and Rawitz) ( PVC) Partial Vertex Cover (Bar-Yehuda) ( GVC) Generalized Vertex Cover (Bar-Yehuda and Rawitz) Applications to some other Approximations: ( SC) Minimum Set Cover (Bar-Yehuda and Even) ( PSC) Partial Set Cover (Bar-Yehuda) ( MSP) Maximum Set Packing (Arkin and Hasin) Applications Resource Allocation and Scheduling : …. 6

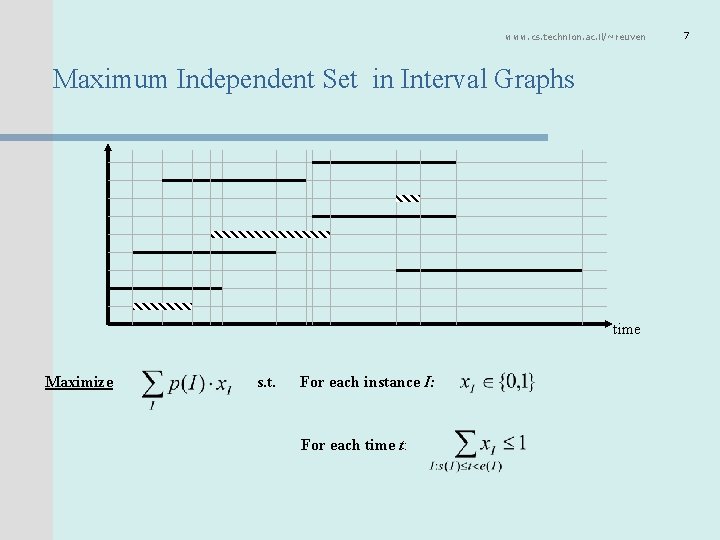
www. cs. technion. ac. il/~reuven Maximum Independent Set in Interval Graphs time Maximize s. t. For each instance I: For each time t: 7

Maximum Independent Set in Interval Graphs: How to select P 1 to get optimization? www. cs. technion. ac. il/~reuven P =0 1 P 1=0 P 1=1 P 1=0 P 1=1 Î time Let Î be an interval that ends first; 1 if I in conflict with Î For all intervals I define: p 1 (I) = 0 else For every feasible x: p 1 ·x 1 Every Î-maximal is optimal. For every Î-maximal x: p 1 ·x 1 8

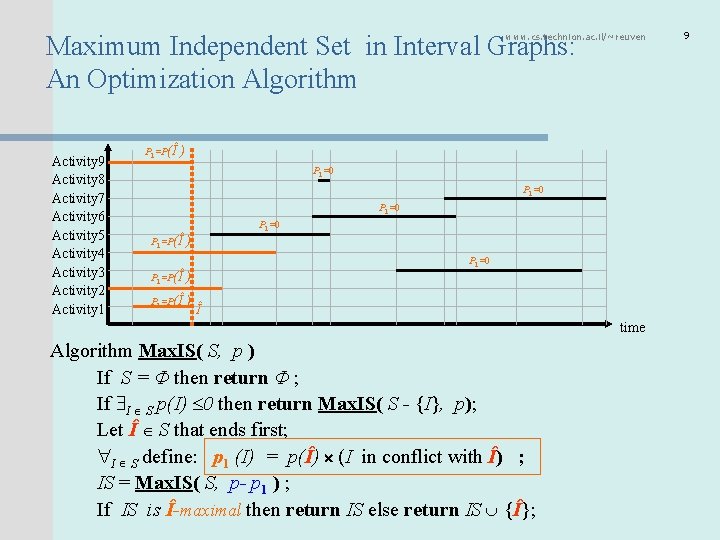
Maximum Independent Set in Interval Graphs: An Optimization Algorithm www. cs. technion. ac. il/~reuven P 1=P(Î ) Activity 9 P 1=0 Activity 8 P 1=0 Activity 7 P 1=0 Activity 6 P 1=0 Activity 5 P 1=P(Î ) Activity 4 P 1=0 Activity 3 P 1=P(Î ) Activity 2 P 1=P(Î ) Activity 1 Î time Algorithm Max. IS( S, p ) If S = Φ then return Φ ; If I S p(I) 0 then return Max. IS( S - {I}, p); Let Î S that ends first; I S define: p 1 (I) = p(Î) (I in conflict with Î) ; IS = Max. IS( S, p- p 1 ) ; If IS is Î-maximal then return IS else return IS {Î}; 9

www. cs. technion. ac. il/~reuven Maximum Independent Set in Interval Graphs: Running Example P(I 5) = 3 -4 P(I 6) = 6 -4 -2 P(I 3) = 5 -5 P(I 2) = 3 -5 P(I 1) = 5 -5 P(I 4) = 9 -5 -4 -2 10

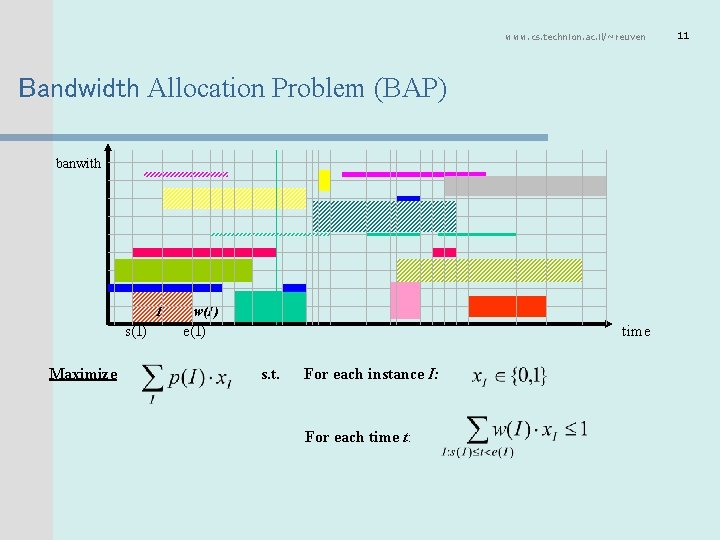
www. cs. technion. ac. il/~reuven Bandwidth Allocation Problem (BAP) banwith I w(I) s(I) e(I) time Maximize s. t. For each instance I: For each time t: 11

www. cs. technion. ac. il/~reuven 12 Bandwidth Allocation Problem (BAP) 1987 Arkin and Silverberg: requests have same duration. 2000 Philips Uma Wein: 6 2001 Bar-Noy Bar-Yehuda Freund Naor Schieber: 3 2002 Chen Hassin Tzur: DP for restricted case. 2002 Calinescu, Chakrabarti, Karloff, Rabani: 2 Randomized Also dynamic programming 2003 Chekuri, Maydlarz, Shepherd: Extentions (e. g. trees) 2005 This talk: 2+1/(e-1) 2. 582

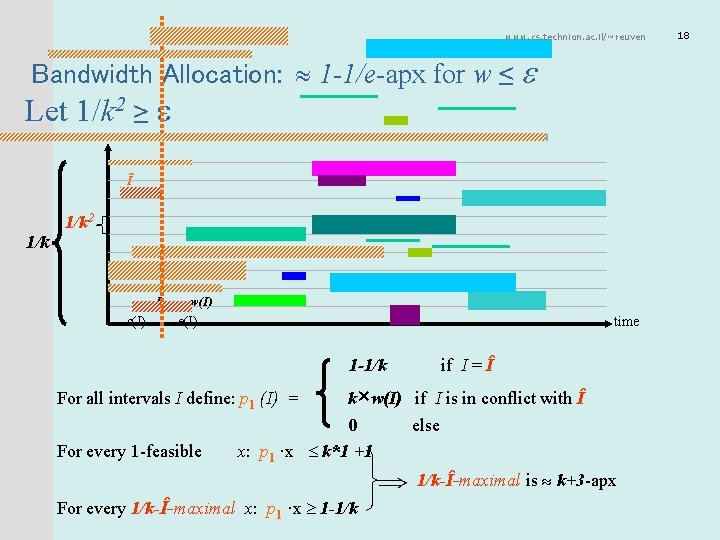
www. cs. technion. ac. il/~reuven 13 Bandwidth Allocation for w 1/2 How to select P 1 to get 1/3 -approximation? Î I w(I) s(I) e(I) time 1 if I = Î For all intervals I define: p 1 (I) = 2*w(I) if I is in conflict with Î 0 else For every feasible x: p 1 ·x 1+2*1 Every Î-maximal is 1/3 -approximation For every Î-maximal x: p 1 ·x 1

www. cs. technion. ac. il/~reuven 14 Bandwidth Allocation for w 1/2 … A better P 1 to get 1/2 -approximation? Î I w(I) s(I) e(I) time 1 For all intervals I define: p 1 (I) = if I = Î w(I)/Ŵ if I is in conflict with Î 0 else Where Ŵ=1 - w(Î) feasible x: p 1 ·x max{ 1+ Ŵ /Ŵ , 1 /Ŵ } Î -maximal is 1/2 -approximation Î-maximal x: p 1 ·x min{1, Ŵ /Ŵ}

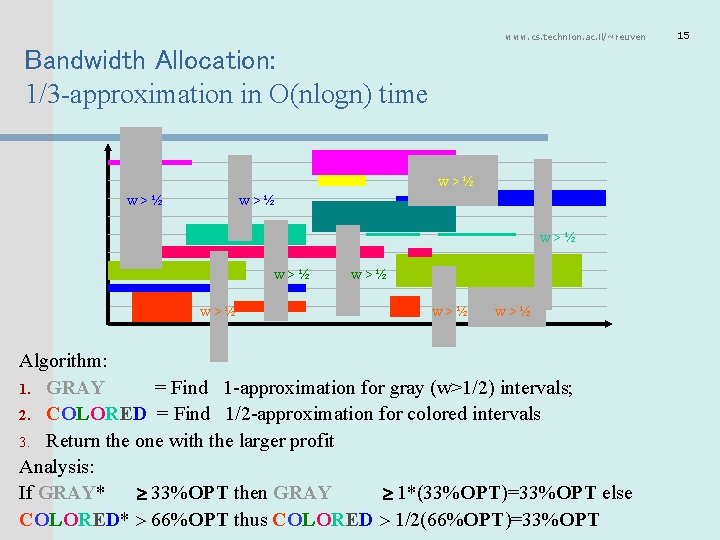
www. cs. technion. ac. il/~reuven Bandwidth Allocation: 1/3 -approximation in O(nlogn) time w > ½ w > ½ w > ½ w > ½ Algorithm: 1. GRAY = Find 1 -approximation for gray (w>1/2) intervals; 2. COLORED = Find 1/2 -approximation for colored intervals 3. Return the one with the larger profit Analysis: If GRAY* 33%OPT then GRAY 1*(33%OPT)=33%OPT else COLORED* 66%OPT thus COLORED 1/2(66%OPT)=33%OPT 15

www. cs. technion. ac. il/~reuven Bandwidth Allocation: What if we get R-approx for w > and r-approx for w ≤ ? w > w > w > w > Algorithm: 1. GRAY = Find R-approximation for gray (w> ) intervals; 2. COLORED = Find r-approximation for colored intervals 3. Return the one with the larger profit Analysis: If GRAY* r/(R+r)×OPT then GRAY R× r/(R+r)×OPT else COLORED* R/(R+r)×OPT thus COLORED r× R/(R+r)×OPT 16

www. cs. technion. ac. il/~reuven Banwidth Allocation: 1 -approx for w > Algorithm: 2002 Chen Hassin Tzur 2002 Calinescu, Chakrabarti, Karloff, Rabani Dynamic Programming R = 1 17

www. cs. technion. ac. il/~reuven Bandwidth Allocation: 1 -1/e-apx for w ≤ Let 1/k 2 ≥ 1/k Î 1/k 2 I w(I) s(I) e(I) time 1 -1/k For all intervals I define: p 1 (I) = if I = Î k×w(I) if I is in conflict with Î 0 else For every 1 -feasible x: p 1 ·x k*1 +1 1/k-Î-maximal is k+3 -apx For every 1/k-Î-maximal x: p 1 ·x 1 -1/k 18

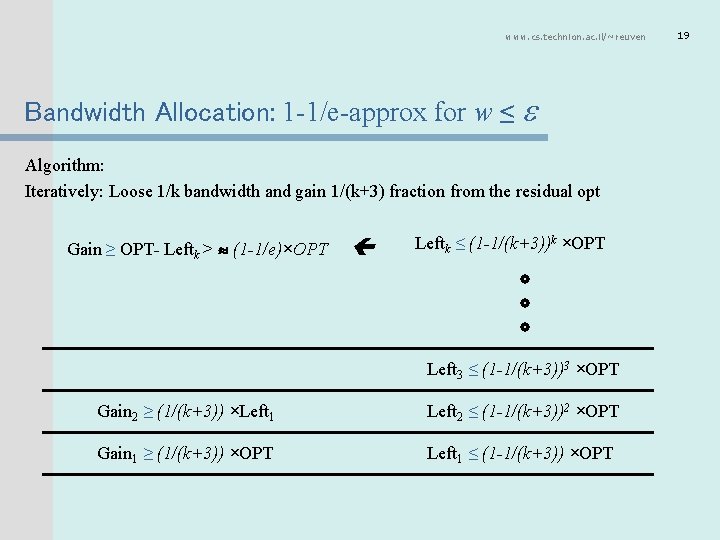
www. cs. technion. ac. il/~reuven Bandwidth Allocation: 1 -1/e-approx for w ≤ Algorithm: Iteratively: Loose 1/k bandwidth and gain 1/(k+3) fraction from the residual opt Gain ≥ OPT- Leftk > (1 -1/e)×OPT Leftk ≤ (1 -1/(k+3))k ×OPT Left 3 ≤ (1 -1/(k+3))3 ×OPT Gain 2 ≥ (1/(k+3)) ×Left 1 Left 2 ≤ (1 -1/(k+3))2 ×OPT Gain 1 ≥ (1/(k+3)) ×OPT Left 1 ≤ (1 -1/(k+3)) ×OPT 19

www. cs. technion. ac. il/~reuven Storage Allocation Problem (SAP) 20

www. cs. technion. ac. il/~reuven Storage Allocation Problem (SAP) 2000 Philips, Uma, Wein: 35 2000 Leonardi, Marchetti-Spaccamela, Vitaletti: 12 2001 Bar-Noy, Bar-Yehuda, Freund, Naor, Schieber: 7 2002 Chen, Hassin, Tzur: DP 2005 This talk: 2+1/(e-1) 2. 582 21

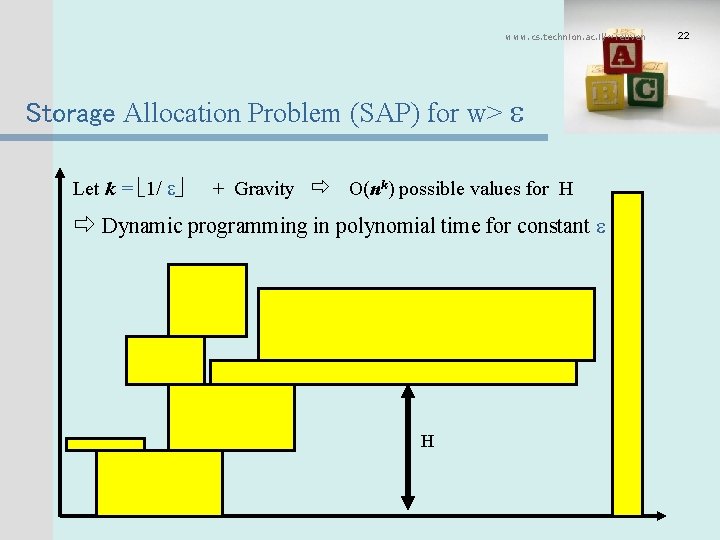
www. cs. technion. ac. il/~reuven Storage Allocation Problem (SAP) for w> Let k = 1/ + Gravity O(nk) possible values for H Dynamic programming in polynomial time for constant H 22

www. cs. technion. ac. il/~reuven For w ≤ R-apx for BAP R-apx for SAP Dynamic Storage Allocation (DSA) Find Min bandwidth with “perfect” SAP allocation Run BAP (w ≤ ) If Load ≤ 1/3 // Load = Max total height at time t use Gergov 99 to get DSA in bandwidth ≤ 1 Else use 2003 Buchsbaum, Karloff, Kenyon, Reingold and Thorup to get DSA in bandwidth ≤ 1 +O( 1/7) Corollary: for w ≤ : 1 -apx randomized 1. 582 -apx (deterministic and combinatorial) Corollary: 2 randomized and 2. 582 deterministic 23

www. cs. technion. ac. il/~reuven Bandwidth Allocation on trees. 2003 Chekuri, Maydlarz, Shepherd: Input: Capacitated tree, where each edge has an integral capacity, and a set of paths, each of which has an integral demand a profit. Solution: A set of paths such that the demands of the paths can be simultaneously routed without violating edge capacities. Results: 4 -approx for the case of unit demands. 48 -approx for the case where max(demand) ≤ min(capacity) Our results: We consider the uniform capacities bounded degree case Note: in this case max(demand) ≤ min(capacity) (2+1/(e 1/2 -1)+ )-approx 3. 54 -aprox (2+1/(e 1/d-1)+ )-approx when we are given a set of trees of degree d (instead of paths). 24

www. cs. technion. ac. il/~reuven Bandwidth Allocation of uniform capacities general demands trees on trees. 25

Bounded degress trees: Bandwidth Allocation: 1 -approx for w > Dynamic Programming R = 1 www. cs. technion. ac. il/~reuven 26

www. cs. technion. ac. il/~reuven Bandwidth Allocation of uniform capacities general demands trees on trees. Let 1/k 2 ≥ 27 1 -1/k if I = Î For all intervals I define: p 1 (I) = k×w(I) if I is in conflict with Î 0 else For every 1 -feasible x: p 1 ·x k*d +1 1/k-Î-maximal is d(k+1)-apx For every 1/k-Î-maximal x: p 1 ·x 1 -1/k

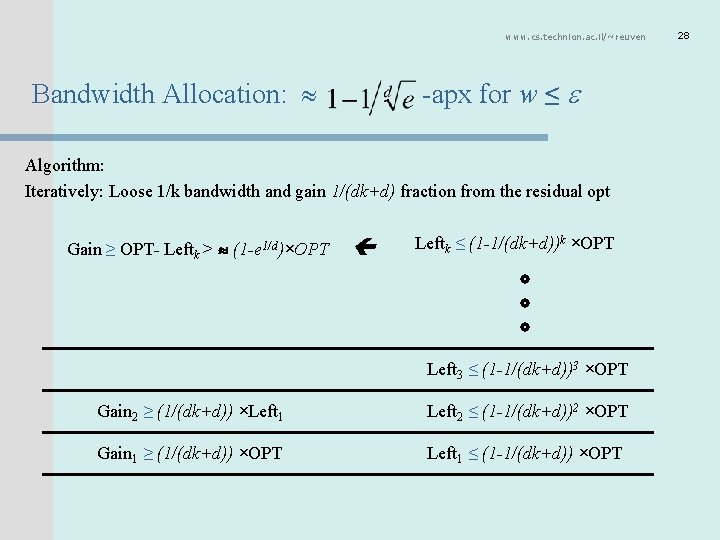
www. cs. technion. ac. il/~reuven -apx for w ≤ Bandwidth Allocation: Algorithm: Iteratively: Loose 1/k bandwidth and gain 1/(dk+d) fraction from the residual opt Gain ≥ OPT- Leftk > (1 -e 1/d)×OPT Leftk ≤ (1 -1/(dk+d))k ×OPT Left 3 ≤ (1 -1/(dk+d))3 ×OPT Gain 2 ≥ (1/(dk+d)) ×Left 1 Left 2 ≤ (1 -1/(dk+d))2 ×OPT Gain 1 ≥ (1/(dk+d)) ×OPT Left 1 ≤ (1 -1/(dk+d)) ×OPT 28