Approximation Algorithms Chapter 1 Introduction Why Approximation Algorithms

Approximation Algorithms Chapter 1 - Introduction

Why Approximation Algorithms Ø Problems that we cannot find an optimal solution in a polynomial time q Eg: Set Cover, Bin Packing Ø Need to find a near-optimal solution: q Heuristic q Approximation algorithms: § This gives us a guarantee approximation ratio 2 Passion is the key to success

Why take this course Ø Your advisers/bosses give you a computationally hard problem. Here are two scenarios: q No knowledge about approximation: § Spend a few months looking for an optimal solution § Come to their office and confess that you cannot do it § Get fired q Knowledge about approximation: Passion is the key to success 3

Why take this course (cont) Ø Knowledge about approximation q Show your boss that this is a NP-complete (NPhard) problem q There does not exist any polynomial time algorithm to find an exact solution q Propose a good algorithm (either heuristic or approximation) to find a near-optimal solution q Better yet, prove the approximation ratio Passion is the key to success 4

Course Description Ø Covers a variety of techniques to design and analyze many approximation algorithms for computationally hard problems: q Combinatorial algorithms: § Greedy Techniques, Independent System, Submodular Function § Cover various problems q Linear Programming based algorithms q Semidefinite Programming based algorithms Passion is the key to success 5

Course Objectives Ø Grasp the essential techniques to design and analyze approximation algorithms: q q q Combinatorial methods Linear programming Semidefinite programming Primal-dual and relaxation methods Hardness of approximation Ø Grasp the key ideas of graph theory Ø Able to model and solve many practical problems raising in our real life Passion is the key to success 6

Textbooks Ø Recommended: q Vijay Vazirani, Approximation Algorithms, Springer. Verlag, 2001 q Vasek Chvatal, Linear Programming, W. H. Freeman Company q Michael R. Garey and David S. Johnson, Computers and Intractability: A Guide to the Theory of NP-Completeness Ø Shall provide appropriate lecture notes Passion is the key to success 7

Introduction to Combinatorial Optimization Passion is the key to success 8

Combinatorial Optimization Ø The study of finding the “best” object from within some finite space of objects, eg: q Shortest path: Given a graph with edge costs and a pair of nodes, find the shortest path (least costs) between them q Traveling salesman: Given a complete graph with nonnegative edge costs, find a minimum cost cycle visiting every vertex exactly once q Maximum Network Lifetime: Given a wireless sensor networks and a set of targets, find a schedule of these sensors to maximize network lifetime Passion is the key to success 9

In P or not in P? Informal Definitions: Ø The class P consists of those problems that are solvable in polynomial time, i. e. O(nk) for some constant k where n is the size of the input. Ø The class NP consists of those problems that are “verifiable” in polynomial time: q Given a certificate of a solution, then we can verify that the certificate is correct in polynomial time Passion is the key to success 10

In P or not in P: Examples Ø In P: q Shortest path q Minimum Spanning Tree Ø Not in P (NP): q Vertex Cover q Traveling salesman q Minimum Connected Dominating Set Passion is the key to success 11

NP-completeness (NPC) Ø A problem is in the class NPC if it is in NP and is as “hard” as any problem in NP Passion is the key to success 12

What is “hard” Ø Decision Problems: Only consider YES-NO q Decision version of TSP: Given n cities, is there a TSP tour of length at most L? Ø Why Decision Problem? What relation between the optimization problem and its decision? q Decision is not “harder” than that of its optimization problem q If the decision is “hard”, then the optimization problem should be “hard” Passion is the key to success 13

NP-complete and NP-hard A language L is NP-complete if: 1. L is in NP, and 2. For every L’ in NP, L’ can be polynomialtime reducible to L Passion is the key to success 14

Approximation Algorithms Ø An algorithm that returns near-optimal solutions in polynomial time Ø Approximation Ratio ρ(n): q Define: C* as a optimal solution and C is the solution produced by the approximation algorithm q max (C/C*, C*/C) <= ρ(n) q Maximization problem: 0 < C <= C*, thus C*/C shows that C* is larger than C by ρ(n) q Minimization problem: 0 < C* <= C, thus C/C* shows that C is larger than C* by ρ(n) Passion is the key to success 15

Approximation Algorithms (cont) Ø PTAS (Polynomial Time Approximation Scheme): A (1 + ε)-approximation algorithm for a NP-hard optimization П where its running time is bounded by a polynomial in the size of instance I Ø FPTAS (Fully PTAS): The same as above + time is bounded by a polynomial in both the size of instance I and 1/ε Passion is the key to success 16

A Dilemma! Ø We cannot find C*, how can we compare C to C*? Ø How can we design an algorithm so that we can compare C to C* It is the objective of this course!!! Passion is the key to success 17

Techniques Ø A variety of techniques to design and analyze many approximation algorithms for computationally hard problems: q Combinatorial algorithms: § Greedy Techniques, Independent System, Submodular Function q Linear Programming based algorithms q Semidefinite Programming based algorithms Passion is the key to success 18

Vertex Cover Ø Definition: Ø An Example Passion is the key to success 19

Vertex Cover Problem Ø Definition: q Given an undirected graph G=(V, E), find a vertex cover with minimum size (has the least number of vertices) q This is sometimes called cardinality vertex cover Ø More generalization: q Given an undirected graph G=(V, E), and a cost function on vertices c: V → Q+ q Find a minimum cost vertex cover Passion is the key to success 20

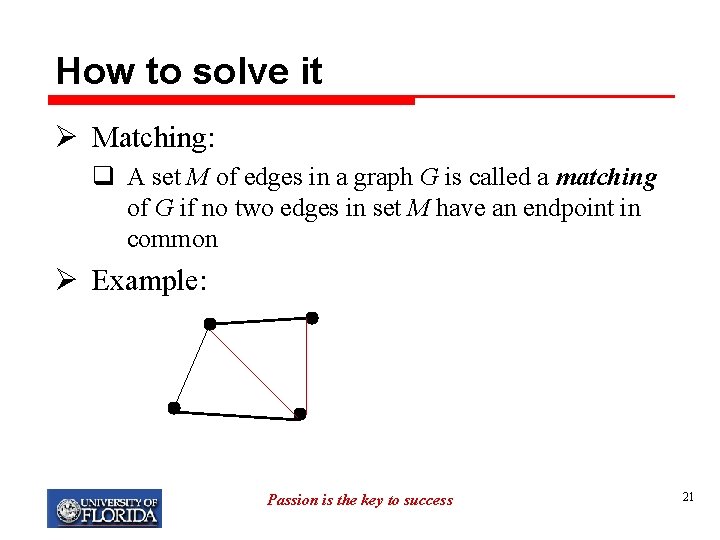
How to solve it Ø Matching: q A set M of edges in a graph G is called a matching of G if no two edges in set M have an endpoint in common Ø Example: Passion is the key to success 21

How to solve it (cont) Ø Maximum Matching: q A matching of G with the greatest number of edges Ø Maximal Matching: q A matching which is not contained in any larger matching Ø Note: Any maximum matching is certainly maximal, but not the reverse Passion is the key to success 22

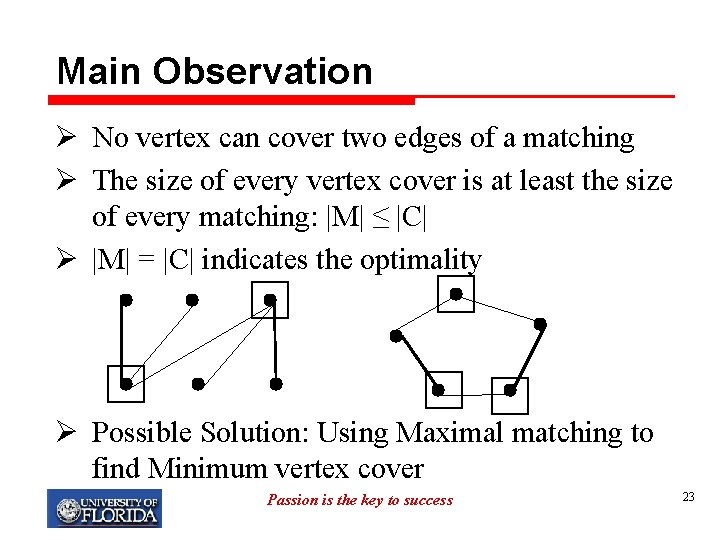
Main Observation Ø No vertex can cover two edges of a matching Ø The size of every vertex cover is at least the size of every matching: |M| ≤ |C| Ø |M| = |C| indicates the optimality Ø Possible Solution: Using Maximal matching to find Minimum vertex cover Passion is the key to success 23

An Algorithm Ø Alg 1: Find a maximal matching in G and output the set of matched vertices Ø Theorem: Alg 1 is a factor 2 -approximation algorithm. Ø Proof: Passion is the key to success 24

Can Alg 1 be improved? Ø Q 1: Can the approximation ratio of Alg 1 be improved by a better analysis? Ø Q 2: Can we design a better approximation algorithm using the similar technique (maximal matching)? Ø Q 3: Is there any other lower bounding method that can lead to a better approximation algorithm? Passion is the key to success 25

Answers Ø A 1: No by considering the complete bipartite graphs Kn, n Ø A 2: No by considering the complete graph Kn where n is odd. q |M| = (n-1)/2 whereas opt = n -1 Passion is the key to success 26

Answers (cont) Ø A 3: q Currently a central open problem q Yes, we can obtain a better one by using the semidefinite programming Ø Generalization vertex Cover q Can we still able to design a 2 -approximation algorithm? q Homework assignment! Passion is the key to success 27

Set Cover Ø Definition: Given a universe U of n elements, a collection of subsets of U, S = {S 1, …, Sm}, and a cost function c: S → Q+, find a minimum cost subcollection C of S that covers all elements of U. Ø Example: q q U = {1, 2, 3, 4, 5} S 1 = {1, 2, 3}, S 2 = {2, 3}, S 3 = {4, 5}, S 4 = {1, 2, 4} c 1 = c 2 = c 3 = c 4 = 1 Solution C = {S 1, S 3} Ø If the cost is uniform, then the set cover problem asks us to find a subcollection covering all elements of U with the minimum size. Passion is the key to success 28

An Example Passion is the key to success 29

NP-completeness Ø Theorem: Set Cover (SC) is NP-complete Ø Proof: INSTANCE: Given a universe U of n elements, a collection of subsets of U, S = {S 1, …, Sm}, and a positive integer b QUESTION: Is there a such that , |C| ≤ b, (Note: The subcollection {Si | } satisfying the above condition is called a set cover of U Passion is the key to success 30

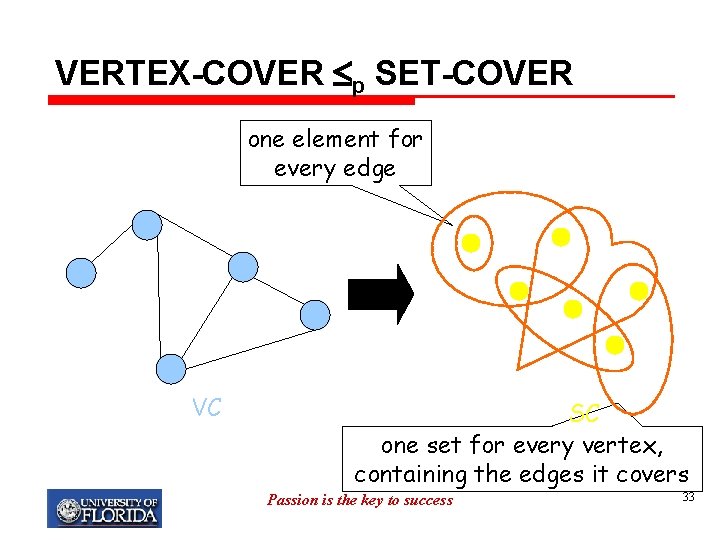
Proof (cont) Ø First we need to show that SC is in NP. Given a subcollection C, it is easy to verify that if |C| ≤ b and the union of all sets listed in C does include all elements in U. Ø To complete the proof, we need to show that Vertex Cover (VC) ≤p Set Cover (SC) Given an instance C of VC (an undirected graph G=(V, E) and a positive integer j), we need to construct an instance C’ of SC in polynomial time such that C is satisfiable iff C’ is satisfiable. Passion is the key to success 31

Proof (cont) Construction: Let U = E. We will define n elements of U and a collection S as follows: Label all vertices in V from 1 to n. Let Si be the set of all edges that incident to vertex i. Finally, let b = j. This construction is in poly-time with respect to the size of VC instance. Note: Each edge corresponds to each element in U and each vertex corresponds to each set in S. Passion is the key to success 32

VERTEX-COVER p SET-COVER one element for every edge VC SC one set for every vertex, containing the edges it covers Passion is the key to success 33

Proof (cont) Now, we need to prove that C is satisfiable iff C’ is. That is, we need to show that if the original instance of VC is a yes instance iff the constructed instance of SC is a yes instance. Ø (→) Suppose G has a vertex cover of size at most j, called C. By our construction, C corresponds to a collection C’ of subsets of U. Since b = j, |C’| ≤ b. Plus, C’ covers all elements in U since C “covers” all edges in G. To see this, consider any element of U. Such an element is an edge in G. Since C is a set cover, at least one endpoint of this edge is in C. Passion is the key to success 34

Ø (←) Suppose there is a set cover C’ of size at most b in our constructed instance. Since each set in C’ is associated with a vertex in G, let C be the set of these vertices. Then |C| = |C’| ≤ b = j. Plus, C is a vertex cover of G since C’ is a set cover. To see this, consider any edge e. Since e is in U, C’ must contain at least one set that includes e. By our construction, the only set that include e correspond to nodes that are endpoints of e. Thus C must contain at least one endpoint of e. Passion is the key to success 35

Solutions Algorithm 1: (in the case of uniform cost) 1: C = empty 2: while U is not empty 3: pick a set Si such that Si covers the most elements in U 4: remove the new covered elements from U 5: C = C union Si 6: return C Passion is the key to success 36

Solutions (cont) Ø In the case of non-uniform cost Ø Similar method. At each iteration, instead of picking a set Si such that Si covers the most uncovered elements, we will pick a set Si whose cost-effectiveness α is smallest, where α is defined as: Ø Questions: Why choose smallest α? Why define α as above Passion is the key to success 37

Solutions (cont) Algorithm 2: (in the case of non-uniform cost) 1: C = empty 2: while U is not empty 3: pick a set Si such that Si has the smallest α 4: for each new covered elements e in U 5: set price(e) = α 6: remove the new covered elements from U 7: C = C union Si 8: return C Passion is the key to success 38

Approximation Ratio Analysis Let ek, k = 1…n, be the elements of U in the order in which they were covered by Alg 2. We have: Ø Lemma 1: Ø Proof: Let Uj denote remaining set U at iteration j. That is, Uj contains all the uncovered elements at iteration j. At any iteration, the leftover sets of the optimal solution can cover the remaining elements at a cost of at most opt. (Why? ) Passion is the key to success 39

Proof of Lemma 1 (cont) Thus, among these leftover sets, there must exist one set where its α value is at most opt/|Uj|. Let ek be the element covered at this iteration, |Uj| ≥ n – k + 1. Since ek was covered by the most cost -effective set in this iteration, we have: price(ek) ≤ opt/|Uj| ≤ opt/(n-k+1) Passion is the key to success 40

Approximation Ratio Ø Theorem 1: The set cover obtained from Alg 2 (also Alg 1) has a factor of Hn where Hn is a harmonic series Hn = 1 + 1/2 + … + 1/n Ø Proof: It follows directly from Lemma 1 Passion is the key to success 41

Examples of NP-complete problems Ø Independent set - independent set: a set of vertices in the graph with no edges between each pair of nodes. - given a graph G=(V, E), find the largest independent set - reduction from vertex cover: smallest vertex cover S largest independent set V/S Passion is the key to success 42

Independent Set Ø Independent set - if G has a vertex cover S, then V S is an independent set proof: consider two nodes in V S: if there is an edge connecting them, then one of them must be in S, which means one of them is not in V S - if G has an independent set I, then V I is a vertex cover proof: consider one edge in G: if it is not covered by any node in V I, then its two end vertices must be both in I, which means I is not an independent set Passion is the key to success 43

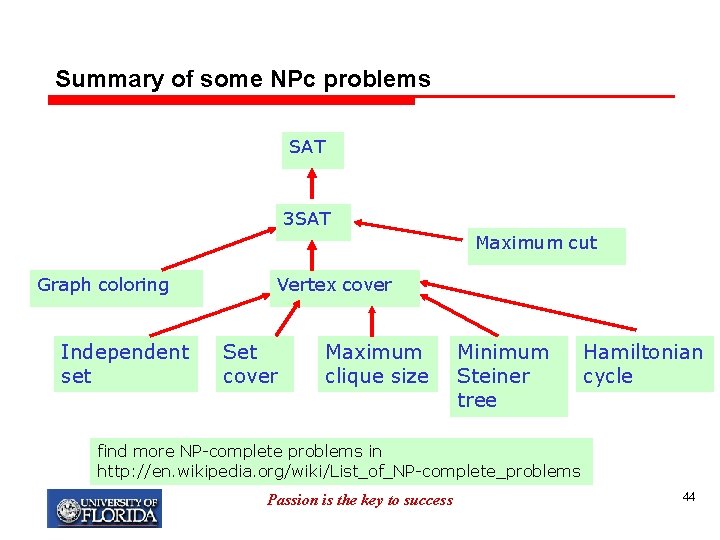
Summary of some NPc problems SAT 3 SAT Maximum cut Graph coloring Independent set Vertex cover Set cover Maximum clique size Minimum Steiner tree Hamiltonian cycle find more NP-complete problems in http: //en. wikipedia. org/wiki/List_of_NP-complete_problems Passion is the key to success 44