Vorlesung 10 Roter Faden Der harmonische Oszillator Der

















- Slides: 32

Vorlesung 10: Roter Faden: Der harmonische Oszillator Der Drehimpuls Folien auf dem Web: http: //www-ekp. physik. uni-karlsruhe. de/~deboer/ Siehe auch: http: //www. wmi. badw-muenchen. de/E 23/lehre/skript/ Wim de Boer, Karlsruhe Atome und Moleküle, 18. 05. 2010 1

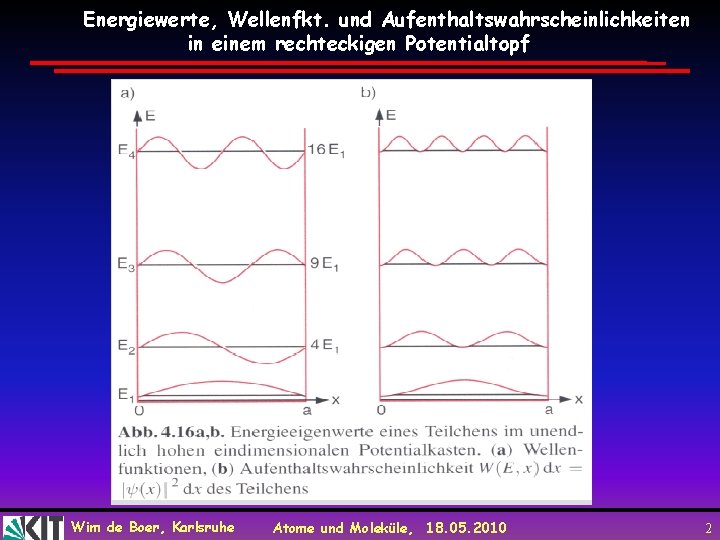
Energiewerte, Wellenfkt. und Aufenthaltswahrscheinlichkeiten in einem rechteckigen Potentialtopf Wim de Boer, Karlsruhe Atome und Moleküle, 18. 05. 2010 2

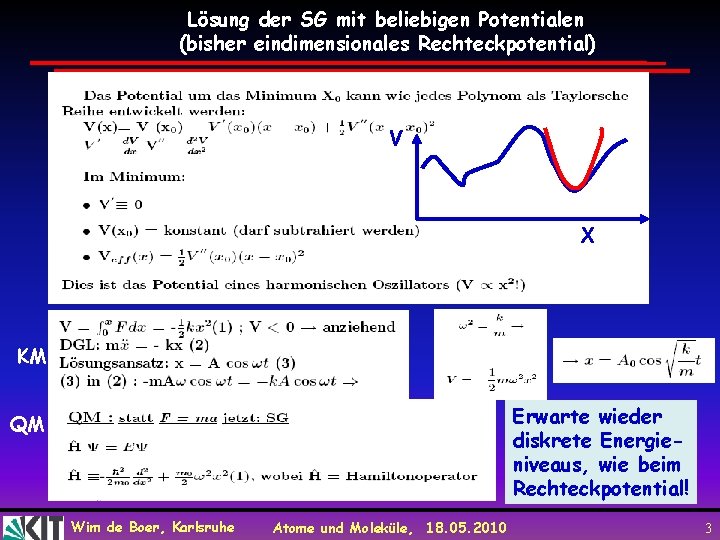
Lösung der SG mit beliebigen Potentialen (bisher eindimensionales Rechteckpotential) V X KM Erwarte wieder diskrete Energieniveaus, wie beim Rechteckpotential! QM Wim de Boer, Karlsruhe Atome und Moleküle, 18. 05. 2010 3

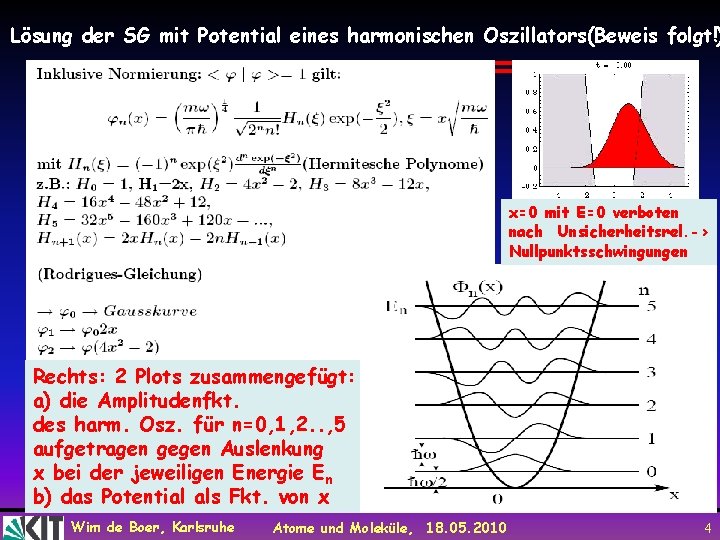
Lösung der SG mit Potential eines harmonischen Oszillators(Beweis folgt!) x=0 mit E=0 verboten nach Unsicherheitsrel. -> Nullpunktsschwingungen Rechts: 2 Plots zusammengefügt: a) die Amplitudenfkt. des harm. Osz. für n=0, 1, 2. . , 5 aufgetragen gegen Auslenkung x bei der jeweiligen Energie En b) das Potential als Fkt. von x Wim de Boer, Karlsruhe Atome und Moleküle, 18. 05. 2010 4

Lösung der SG mit Potential eines harmonischen Oszillators für V=cx 2 (wie vorher beim Rechteckpotential) Der Kommutator [a-a+]=ħω ≠ 0, d. h. nicht gleichzeitig Eigenfkt. von a- und a+. Kettenregel auf xf anwenden! Wim de Boer, Karlsruhe Atome und Moleküle, 18. 05. 2010 5

Lösung der SG mit Potential eines harmonischen Oszillators 1. - + Energiestufen von ħω ist gerade das, was man braucht um diskrete Energieniveaus eines harm. Osz. zu beschreiben. Wim de Boer, Karlsruhe Atome und Moleküle, 18. 05. 2010 6

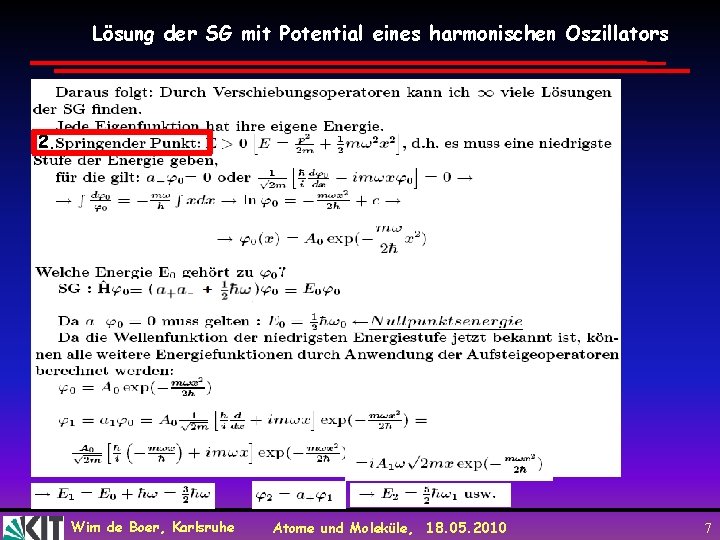
Lösung der SG mit Potential eines harmonischen Oszillators 2. Wim de Boer, Karlsruhe Atome und Moleküle, 18. 05. 2010 7

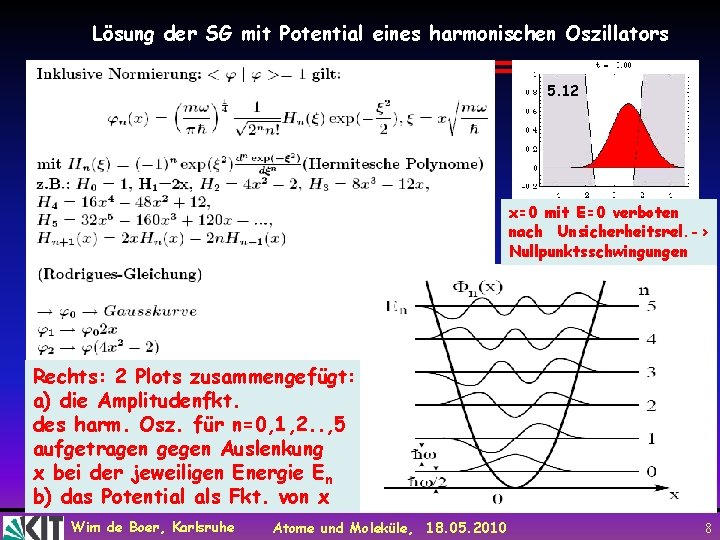
Lösung der SG mit Potential eines harmonischen Oszillators 5. 12 x=0 mit E=0 verboten nach Unsicherheitsrel. -> Nullpunktsschwingungen Rechts: 2 Plots zusammengefügt: a) die Amplitudenfkt. des harm. Osz. für n=0, 1, 2. . , 5 aufgetragen gegen Auslenkung x bei der jeweiligen Energie En b) das Potential als Fkt. von x Wim de Boer, Karlsruhe Atome und Moleküle, 18. 05. 2010 8

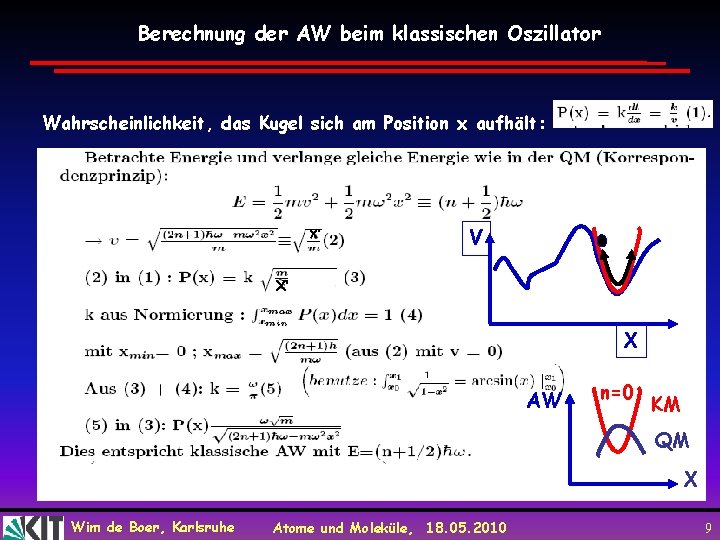
Berechnung der AW beim klassischen Oszillator Wahrscheinlichkeit, das Kugel sich am Position x aufhält: X’ V X’ X AW n=0 KM QM X Wim de Boer, Karlsruhe Atome und Moleküle, 18. 05. 2010 9

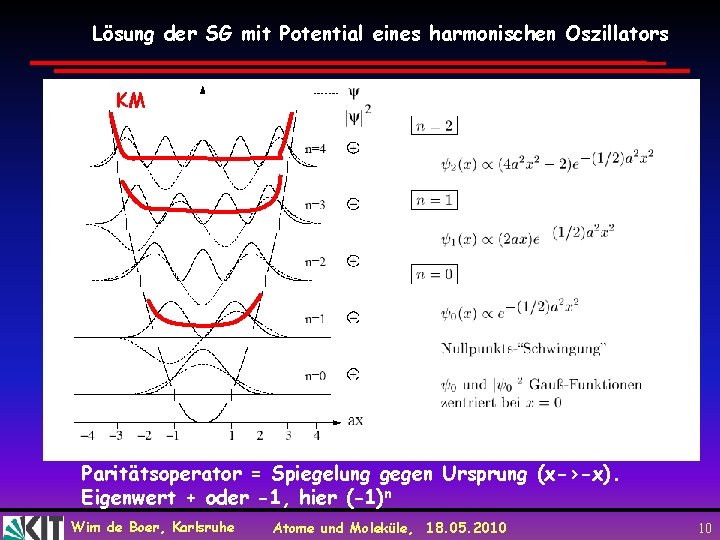
Lösung der SG mit Potential eines harmonischen Oszillators KM Paritätsoperator = Spiegelung gegen Ursprung (x->-x). Eigenwert + oder -1, hier (-1)n Wim de Boer, Karlsruhe Atome und Moleküle, 18. 05. 2010 10

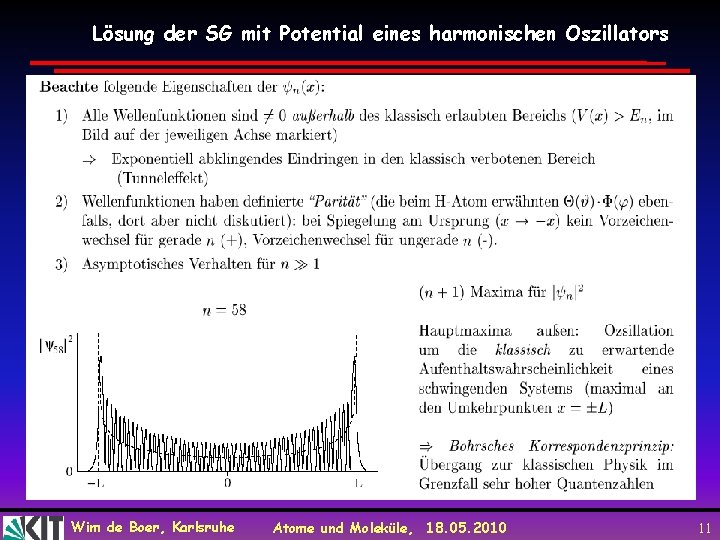
Lösung der SG mit Potential eines harmonischen Oszillators Wim de Boer, Karlsruhe Atome und Moleküle, 18. 05. 2010 11

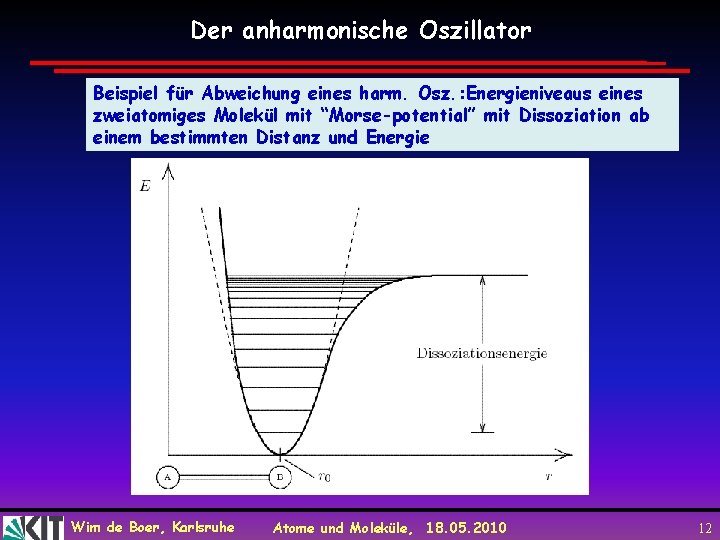
Der anharmonische Oszillator Beispiel für Abweichung eines harm. Osz. : Energieniveaus eines zweiatomiges Molekül mit “Morse-potential” mit Dissoziation ab einem bestimmten Distanz und Energie Wim de Boer, Karlsruhe Atome und Moleküle, 18. 05. 2010 12

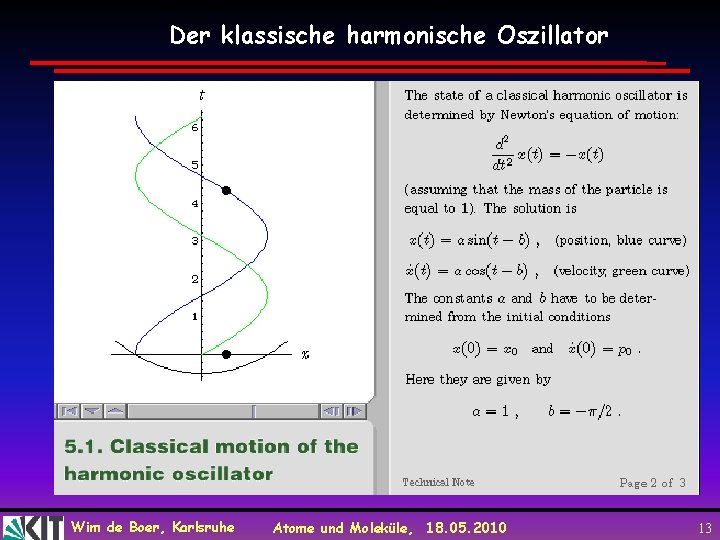
Der klassische harmonische Oszillator Wim de Boer, Karlsruhe Atome und Moleküle, 18. 05. 2010 13

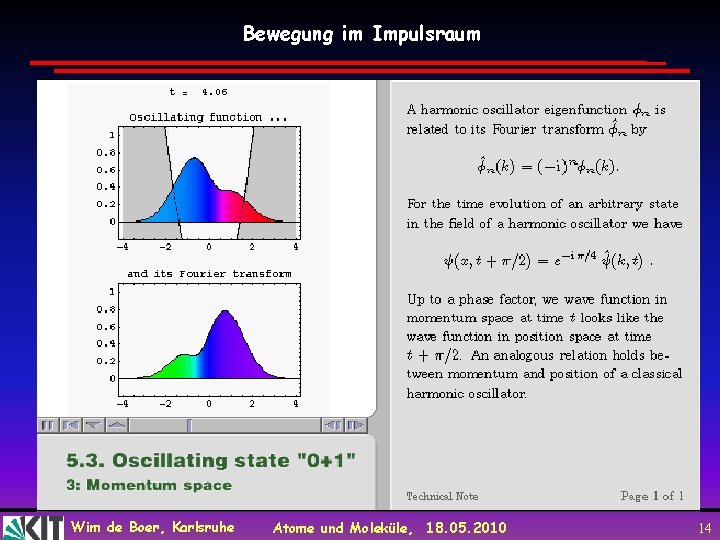
Bewegung im Impulsraum Wim de Boer, Karlsruhe Atome und Moleküle, 18. 05. 2010 14

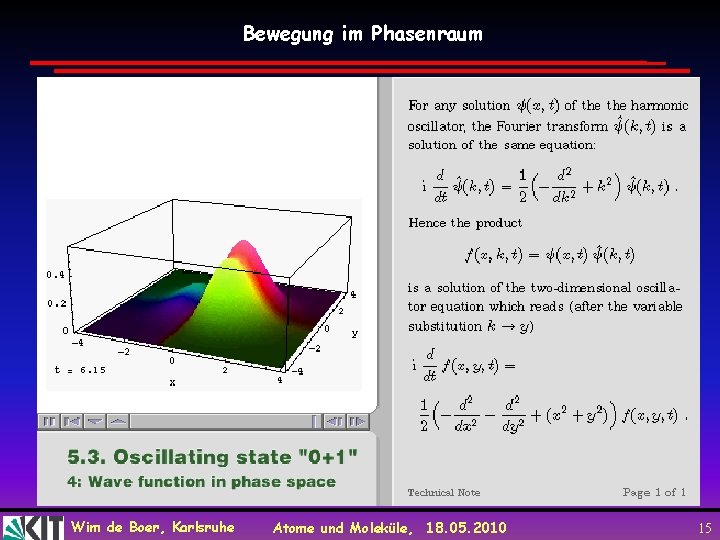
Bewegung im Phasenraum Wim de Boer, Karlsruhe Atome und Moleküle, 18. 05. 2010 15

Der Drehimpuls Im kugelsymmetrischen Coulombpotential gibt es nur radiale Kräfte, d. h. keine Drehmomente auf das Elektron im H-Atom! Daher erwarte ich Drehimpulserhaltung im Falle der Kugelsymmetrie und Wellenfkt. sollte Eigenfkt. des Drehimpulsoperators sein. Bei mehreren Elektronen wird Kugelsymmetrie aufgehoben-> kleine Störungen -> können nur numerisch berechnet werden. Hier nur Einelektron-Atome. Wim de Boer, Karlsruhe Atome und Moleküle, 18. 05. 2010 16

Mathematisches Intermezzo Kartesische Koordinaten: später mehr Kugelkoord. : dsr=dr dsθ=r dθ dsφ=r sinθ dφ Wim de Boer, Karlsruhe Atome und Moleküle, 18. 05. 2010 17

Hamiltonoperator für kugelsymmetrisches Potential Wim de Boer, Karlsruhe Atome und Moleküle, 18. 05. 2010 18

Vertauschungsrelationen Kurzform: Wim de Boer, Karlsruhe Atome und Moleküle, 18. 05. 2010 19

Vertauschungsrelationen Gesamtdrehimpuls und eine der Komponenten nur gleichzeitig zu bestimmmen. Gesamtdrehimpuls und Energie gleichzeitig zu bestimmmen. Z-Komponente des Drehimpulses und Energie gleichzeitig zu bestimmmen. Eigenfunktionsgleichungen: Wim de Boer, Karlsruhe Atome und Moleküle, 18. 05. 2010 20

Drehimpuls in der QM Während also in der klassischen Mechanik der Drehimpuls eines Teilchen, das sich einem kugelsymmetrischen Potential bewegt, nach Betrag und Richtung zeitlich konstant ist, sagt die QM, dass zwar der Betrag des Drehimpulses zeitlich konstant ist, dass aber von seinen drei Komponenten nur einen zeitlich konstanten Messwert besitzt! Dies kann man auffassen als eine Präzession des Drehimpulses um die Achse mit dem konstanten Messwert. Weiter sind die konstante Komponenten quantisiert mit Eigenwerten l(l+1) ħ für Ȋ und mħ für Ȋ z mit –l<m<l Beweis folgt Wim de Boer, Karlsruhe Atome und Moleküle, 18. 05. 2010 21

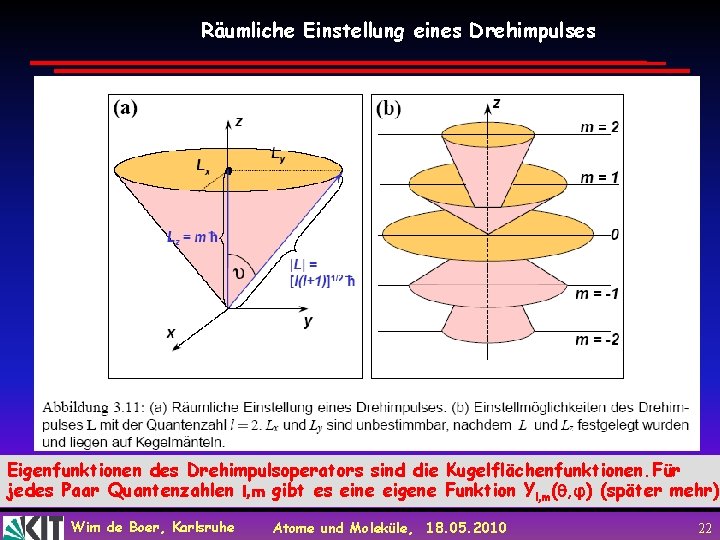
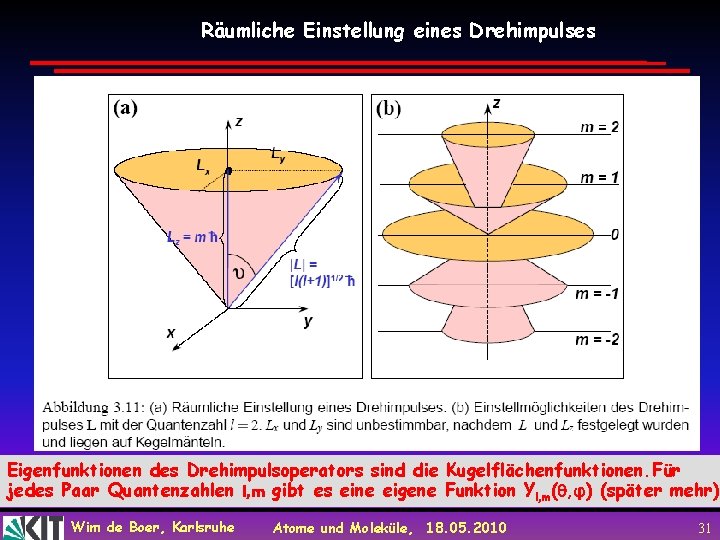
Räumliche Einstellung eines Drehimpulses Eigenfunktionen des Drehimpulsoperators sind die Kugelflächenfunktionen. Für jedes Paar Quantenzahlen l, m gibt es eine eigene Funktion Yl, m( , φ) (später mehr) Wim de Boer, Karlsruhe Atome und Moleküle, 18. 05. 2010 22

Mathematisches Intermezzo Wim de Boer, Karlsruhe Atome und Moleküle, 18. 05. 2010 23

Mathematisches Intermezzo Beweis folgt Wim de Boer, Karlsruhe Atome und Moleküle, 18. 05. 2010 24

Drehimpulsoperator von kartesischen Koor. in Kugelkoordinaten umwandeln Wim de Boer, Karlsruhe Atome und Moleküle, 18. 05. 2010 25

Drehimpulsoperator von kartesischen Koor. in Kugelkoordinaten umwandeln Wim de Boer, Karlsruhe Atome und Moleküle, 18. 05. 2010 26

Stehende Wellen auf einem Kreis Betrachte stehende Wellen auf einem Kreis (cosφ oder eimφ) Randbedingung: Φ (φ)= Φ (φ+2 ) oder Aeimφ = Aeim(φ+2 ) m=0, ± 1, ± 2. . (Quantisierung durch Randbedingung!) Betrachte Φ (φ)= =ħm Φ (φ) Þz-Wert des Drehimpulses ist quantisiert! Wie groß ist Gesamtdrehimpuls, d. h. Erwartung von Wim de Boer, Karlsruhe Atome und Moleküle, 18. 05. 2010 27

Eigenwert des Drehimpulses ist √l(l+1) ħ + Da Lz immer kleiner als Ltot muss gelten: |m|≤ l und l ≥ 0, l = 0, 1, 2, 3 Wim de Boer, Karlsruhe Atome und Moleküle, 18. 05. 2010 28

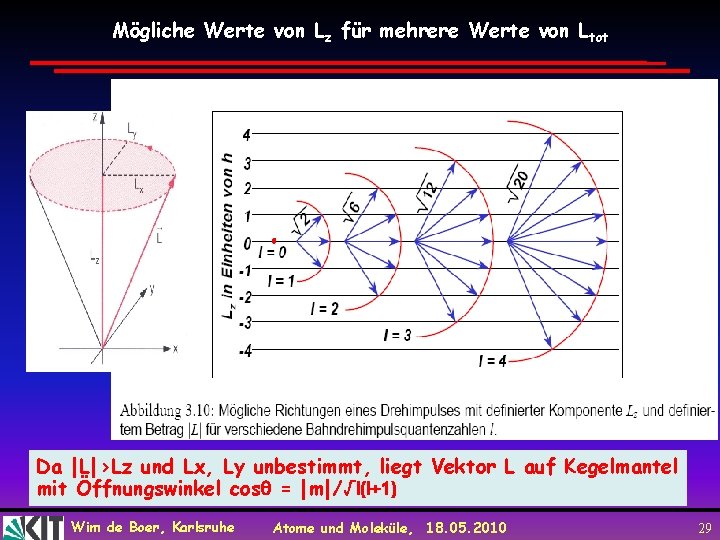
Mögliche Werte von Lz für mehrere Werte von Ltot Da |L|>Lz und Lx, Ly unbestimmt, liegt Vektor L auf Kegelmantel mit Öffnungswinkel cos = |m|/√l(l+1) Wim de Boer, Karlsruhe Atome und Moleküle, 18. 05. 2010 29

Zusammenfassung Drehimpuls Wim de Boer, Karlsruhe Atome und Moleküle, 18. 05. 2010 30

Räumliche Einstellung eines Drehimpulses Eigenfunktionen des Drehimpulsoperators sind die Kugelflächenfunktionen. Für jedes Paar Quantenzahlen l, m gibt es eine eigene Funktion Yl, m( , φ) (später mehr) Wim de Boer, Karlsruhe Atome und Moleküle, 18. 05. 2010 31

Zum Mitnehmen Die Randbedingungen der SG führen zur Quantisierung der Energien Ein beliebiges Potential kann im Minimum als quadratisches Potential angenähert werden (Taylor-Entwicklung). Dies entspricht das Potential eines harmonischen Oszillators, dessen Energien wieder quantisiert sind. Die Wellenfunktionen der einzelnen Energieniveaus können elegant mit Aufsteige- und Absteigeoperatoren bestimmt werde. Drehimpulse sind quantisiert: Wim de Boer, Karlsruhe Atome und Moleküle, 18. 05. 2010 32
 Roter faden physik
Roter faden physik Nullpunktsenergie harmonischer oszillator
Nullpunktsenergie harmonischer oszillator Newtonsche bewegungsgleichung
Newtonsche bewegungsgleichung Alpha zerfall tunneleffekt
Alpha zerfall tunneleffekt Eleonore franz
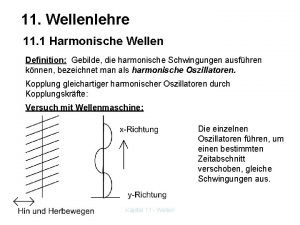
Eleonore franz Harmonische welle definition
Harmonische welle definition Tangentiele versnelling
Tangentiele versnelling Tangentiele versnelling
Tangentiele versnelling Vorlesung
Vorlesung Vorlesung finanzmathematik
Vorlesung finanzmathematik Vorlesung
Vorlesung Gesamtbanksteuerung vorlesung
Gesamtbanksteuerung vorlesung De morgansche regel
De morgansche regel Rechtsobjekt
Rechtsobjekt Hazardfehler
Hazardfehler Gesamtbanksteuerung
Gesamtbanksteuerung Gesamtbanksteuerung vorlesung
Gesamtbanksteuerung vorlesung Weltuntergangstheorie
Weltuntergangstheorie Wer ist der gründer der modernen türkei
Wer ist der gründer der modernen türkei Geschichte vom frosch und skorpion
Geschichte vom frosch und skorpion Aufbau ritterburg
Aufbau ritterburg Gott der stadt gedicht
Gott der stadt gedicht Gegenstand der arbeitspsychologie
Gegenstand der arbeitspsychologie Erste tag der woche
Erste tag der woche Der seele heimat ist der sinn
Der seele heimat ist der sinn Der daumen pflückt die pflaumen
Der daumen pflückt die pflaumen Sorrowing old man painting
Sorrowing old man painting Der weg der atemluft
Der weg der atemluft Albert van der kaap
Albert van der kaap Gegenströmungen zum naturalismus
Gegenströmungen zum naturalismus Zielbereiche der personalentwicklung
Zielbereiche der personalentwicklung Gedicht löwenzahn guggenmos
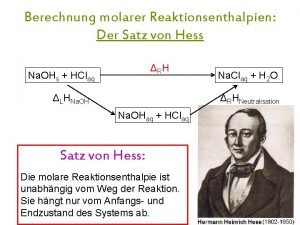
Gedicht löwenzahn guggenmos Satz von hess definition
Satz von hess definition