WS 2015 16 Ulrich Hohenester 8 Vorlesung Harmonischer

WS 2015 / 16 – Ulrich Hohenester 8. Vorlesung Harmonischer Oszillator Molekülschwingungen

Schwingungen von makroskopischen Objekten

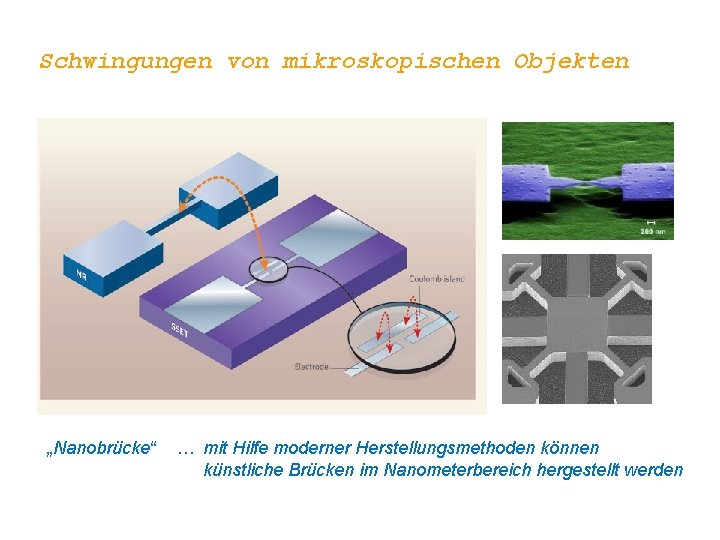
Schwingungen von mikroskopischen Objekten „Nanobrücke“ … mit Hilfe moderner Herstellungsmethoden können künstliche Brücken im Nanometerbereich hergestellt werden

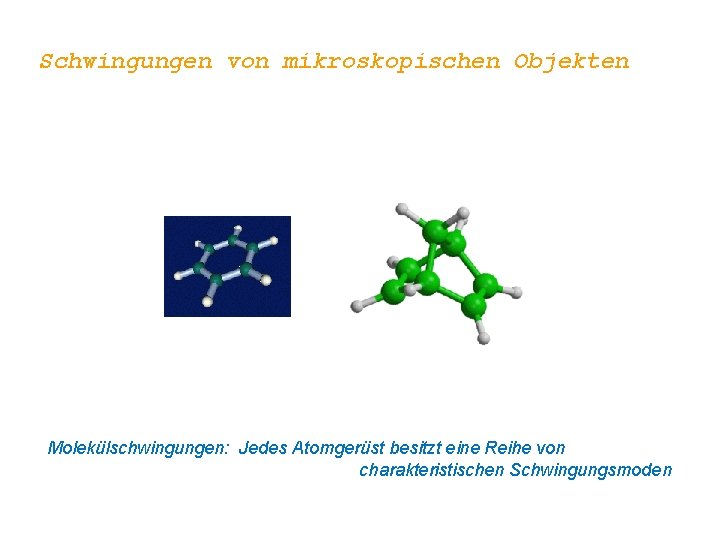
Schwingungen von mikroskopischen Objekten Molekülschwingungen: Jedes Atomgerüst besitzt eine Reihe von charakteristischen Schwingungsmoden

Klassischer harmonischer Oszillator § Newtonsche Bewegunsgleichungen § Eigenfrequenz § Potentielle Energie

Klassischer harmonischer Oszillator Dimensionslose Zeiteinheit Newtonsche Bewegungsgleichungen Bewegungsgleichung kann in der komplexen Ebene gelöst werden, Hilfsgröße a Bewegungsgleichung für Hilfsgröße a Lösung für Auslenkung x

Quantenmechanischer Oszillator Der Hamiltonoperator für den harmonischen Oszillator besteht aus der kinetischen Energie ~p 2 und der potentiellen Energie ~x 2 Jedes Potential kann um Minimum entwickelt werden

Quantenmechanischer Oszillator Es ist in vielen Fällen günstig, dimensionslose Größen für die Impuls- und Ortskoordinaten einzuführen § Charakteristische Längenskala § Dimensionslose Ortsvariable § Dimensionslose Energievariable

Oszillator : dimensionslose Größen In den dimensionslosen Einheiten hat die zeitunabhängige Schrödingergleichung eine einfache Form § Charakteristische Längenskala § Zeitunabhängige Schrödingergleichung in den dimensionlosen Einheiten § Dimensionsloser Impuls und Wellenfunktion

Oszillator : „Leiteroperatoren a“ Wie beim klassischen Oszillator versuchen wir, das Problem durch die Hilfsgröße a zu lösen § Produkt der Operatoren a und a+ § Hamiltonoperator ausgedrückt durch den Operator a

Oszillator : „Leiteroperatoren a“ Wenn ein Eigenzustand von H ist, dann ist auch Zur Lösung des Problems benötigen wir nur die „Kommutatoren“ Insbesondere gilt einer

Oszillator : „Leiteroperatoren a“ Wenn ein Eigenzustand von H ist, dann ist auch einer Nehmen wir an, dass f( q ) ein Eigenzustand ist Durch Anwenden der Operatoren a und a+ erhalten wir neue Eigenzustände a erniedrigt den Energieeigenwert um 1, und a+ erhöht ihn um 1 !!!

Oszillator : Grundzustand + Anregungszustände Damit es einen Grundzustand f 0( q ) gibt, muss für diesen gelten Die Energie des Grundzustandes beträgt Durch Anwenden der „Leiteroperatoren“ kann man alle angeregten Zustände bestimmen

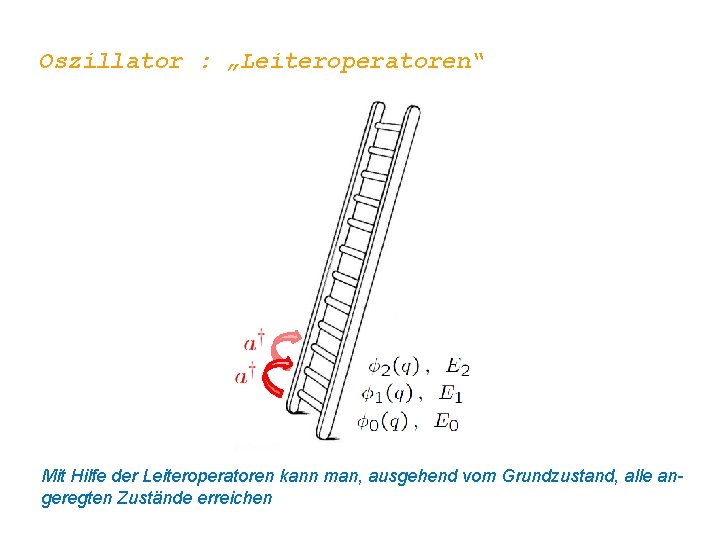
Oszillator : „Leiteroperatoren“ Mit Hilfe der Leiteroperatoren kann man, ausgehend vom Grundzustand, alle angeregten Zustände erreichen

Oszillator : Hermitpolynome Die Eigenzustände des harmonischen Oszillators können auch durch die Hermitpolynome ausgedrückt werden Charles Hermite (1822 – 1901)

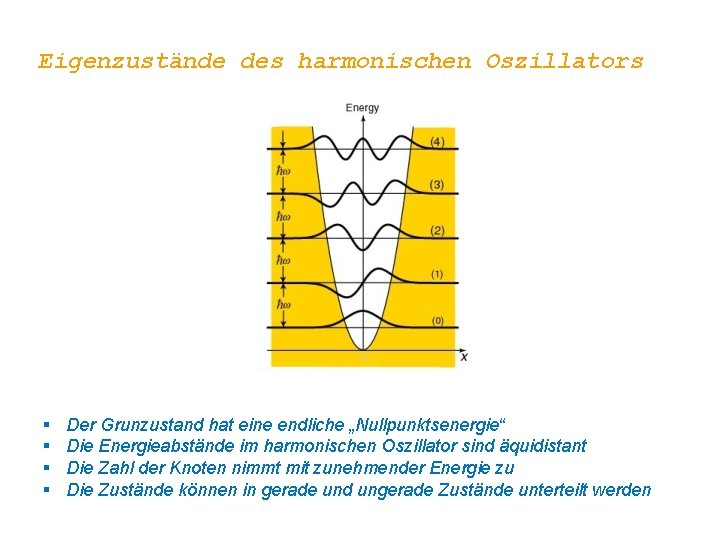
Eigenzustände des harmonischen Oszillators Zeitunabhängige Schrödingergleichung Eigenenergien und Eigenzustände des harmonischen Oszillators Eigenenergien Eigenfunktionen

Eigenzustände des harmonischen Oszillators § § Der Grunzustand hat eine endliche „Nullpunktsenergie“ Die Energieabstände im harmonischen Oszillator sind äquidistant Die Zahl der Knoten nimmt mit zunehmender Energie zu Die Zustände können in gerade und ungerade Zustände unterteilt werden

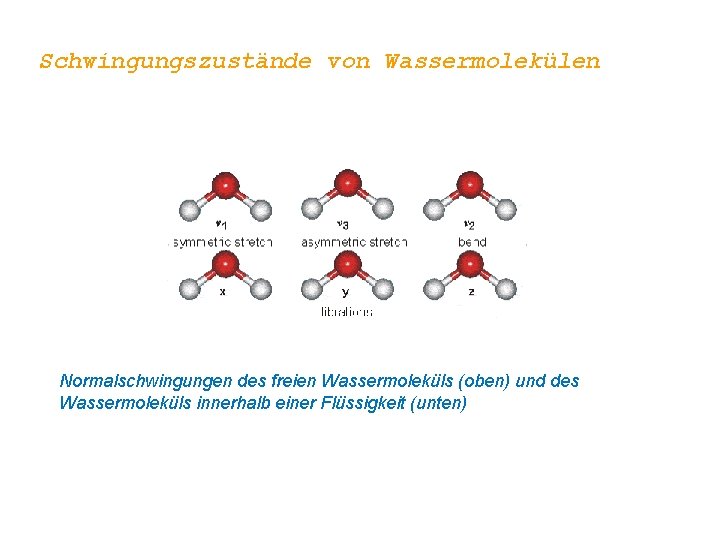
Schwingungszustände von Wassermolekülen Normalschwingungen des freien Wassermoleküls (oben) und des Wassermoleküls innerhalb einer Flüssigkeit (unten)

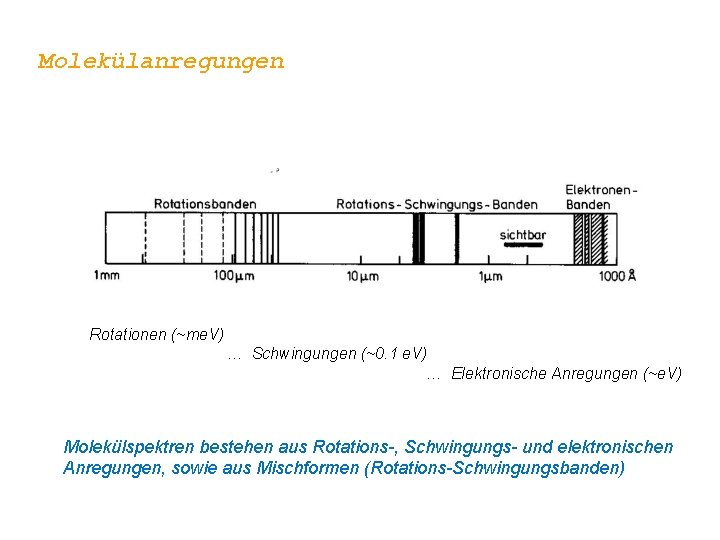
Molekülanregungen Rotationen (~me. V) … Schwingungen (~0. 1 e. V) … Elektronische Anregungen (~e. V) Molekülspektren bestehen aus Rotations-, Schwingungs- und elektronischen Anregungen, sowie aus Mischformen (Rotations-Schwingungsbanden)

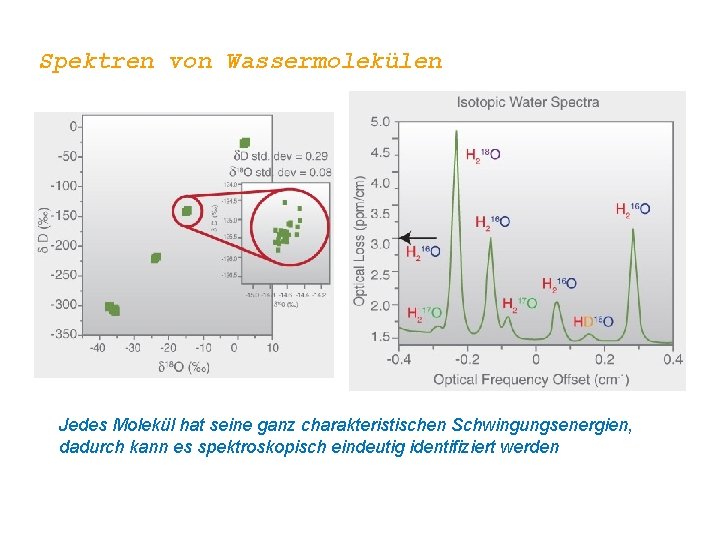
Spektren von Wassermolekülen Jedes Molekül hat seine ganz charakteristischen Schwingungsenergien, dadurch kann es spektroskopisch eindeutig identifiziert werden