Valsznsgszmts felelevent mrc 9 Valsznsgszmts alapjai Esemnytr elemi




















![Korreláció A és valószínűségi változók kovarianciáján a c = M[( - M( ))] értéket Korreláció A és valószínűségi változók kovarianciáján a c = M[( - M( ))] értéket](https://slidetodoc.com/presentation_image_h/d8246375131e1bd2764a8e7f707da467/image-21.jpg)




































- Slides: 67

Valószínűségszámítás felelevenítő márc. 9.

Valószínűségszámítás alapjai Eseménytér ( ), (elemi) események Axiómák: - 0 ≤ P(A) ≤ 1 - P( )=1 - Ha A 1, A 2, … egymást páronként kizáró események (Ai ∩Aj = , ha i j), akkor P( k Ak) = k P(Ak) 2

Tételek - P(Ø) = 0 - P(¬A)=1 -P(A) - P(A B)=P(A)+P(B) – P(A∩B) - P(A) = P(A ∩ B)+P(A ∩¬B) - Ha A B, akkor P(A) ≤ P(B) és P(B-A) = P(B) – P(A) 3

Feltételes valószínűség Amennyiben B igaz, mekkora részben lesz A is igaz. P(A|B) = P(A∩B)/P(B) Következmény (láncszabály): P(A∩B) = P(A|B)·P(B) Egyszerű példa: A: fejfájás, B: influenza P(A) = 1/10, P(B) = 1/40, P(A|B)=? 4

Feltételes valószínűség

Események függetlensége Az A esemény független a B eseménytől akkor és csak akkor ha P(A|B) = P(A) Ez ekvivalens P(AB) = P(A)P(B) illetve P(B|A) = P(B) 6

Általános szorzási szabály A 1, A 2, …, An tetszőleges események, P(A 1 A 2…An) = P(An|A 1…An-1) P(An-1|A 1…An-2)…P(A 2| A 1)P(A 1) Teljes valószínűség tétele: ha A 1, A 2, …, An események teljes eseményrendszert alkotnak, továbbá P(Ai) > 0 minden i-re, akkor P(B) = ∑j=1 n P(B | Ai)P(Ai) 7

Bayes szabály P(A|B) = P(A∩B)/P(B) = P(B|A)P(A)/P(B) 8

Valószínűségi változó ξ: → R Valószínűségi vektorváltozók… Sztochasztikus folyamat: t 9

Eloszlásfüggvény F(x) = P( < x) F(x 1) ≤ F(x 2), ha x 1 < x 2 limx→-∞ F(x) = 0, limx→∞ F(x) = 1 F(x) minden x pontban balról folytonos 10

Diszkrét vs folytonos val. változók Diszkrét: ha lehetséges értékei egy véges vagy végtelen x 1, x 2… sorozatot alkotnak 11

Sűrűségfüggvény Folytonos: ha van olyan f(x) függvény, hogy a számegyenes minden (a, b) intervalluma esetén F(b) - F(a) = P(a < < b) = a∫b f(x)dx Ekkor az f(x) függvényt a valószínűségi változó sűrűségfüggvényének nevezzük. Teljesül: f(x) = F ’(x) és F(x) =. -∞∫x f(t)dt

Hisztogram sűrűségfüggvény empirikus közelítése 13

Valószínűségi változók függetlensége és függetlenek, ha tetszőleges a ≤ b, c ≤ d számok esetén P(a ≤ ≤ b, c ≤ ≤ d) = P(a ≤ ≤ b) P(c ≤ ≤ d). 14

Eloszlások kompozíciója Diszkrét eloszlások kompozíciója = + ahol és függetlenek. Ekkor: rn = P( = n) = k=- P( = n - k, = k) Folytonos függvények kompozíciója hasonló elven, a sűrűségfüggvények megfelelő szorzatának kettős integráljával kapható meg. 15

Várható érték ha lehetséges értékei x 1, x 2, …, és ezeket rendre p 1, p 2, … valószínűségekkel veszi fel, akkor várható értéke: M( ) = i xi pi Folytonos esetben: M( ) = -∞∫ xf(x)dx 16

Várható érték - Ha várható értéke létezik, és c tetszőleges valós szám, akkor c várható értéke is létezik, és M(c ) = c. M( ) - Ha létezik és várható értéke, akkor létezik = + várható értéke is, és M( + ) = M( ) + M( ) 17

Várható érték Ha és független valószínűségi változók, várható értékeik léteznek, akkor létezik a = várható értéke is, és M( ) = M( ) Egy valószínűségi változó A eseményre vonatkoztatott M( |A) feltételes várható értéke a -nek az A eseményre vonatkoztatott feltételes eloszlásának a várható értéke 18

Szórás Egy valószínűségi változó szórása a - M( ) valószínűségi változó négyzetének várható értékéből vont pozitív négyzetgyök: D( ) = (M[( - M( ))2])1/2 Másképpen: D 2( ) = M( 2) – M 2( ) 19

Szórás - Ha szórása létezik, továbbá a és b tetszőleges valós számok, akkor D 2(a + b) = a 2 D 2( ) - Ha 1, 2, …, n független valószínűségi változók, szórásaik léteznek, akkor létezik összegük szórása is és D 2( 1 + 2 + … + n) = D 2( 1) + D 2( 2) + … + D 2( n) 20
![Korreláció A és valószínűségi változók kovarianciáján a c M M értéket Korreláció A és valószínűségi változók kovarianciáján a c = M[( - M( ))] értéket](https://slidetodoc.com/presentation_image_h/d8246375131e1bd2764a8e7f707da467/image-21.jpg)
Korreláció A és valószínűségi változók kovarianciáján a c = M[( - M( ))] értéket értjük (0, ha függetlenek), ha = , akkor a kovariancia a D 2( ) szórásnégyzettel egyezik meg. A és valószínűségi változók korrelációs együtthatója: r = c / ((D( )), értéke -1 és 1 között van. 21

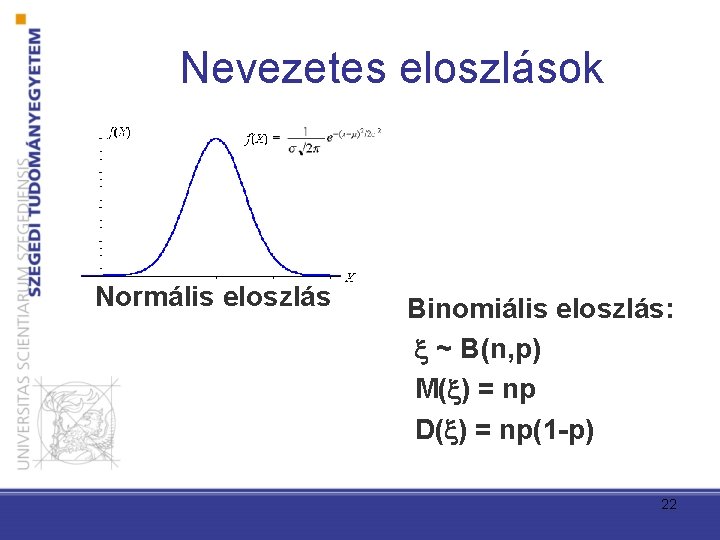
Nevezetes eloszlások Normális eloszlás Binomiális eloszlás: ~ B(n, p) M( ) = np D( ) = np(1 -p) 22

Bayes döntéselmélet

24 Osztályozás – Felügyelt (induktív) tanulás: tanító halmaz alapján olyan modell tanulása ami korábban nem látott példákon is helyesen működik. – Osztályozás: előre definiált kategóriákba besorolás.

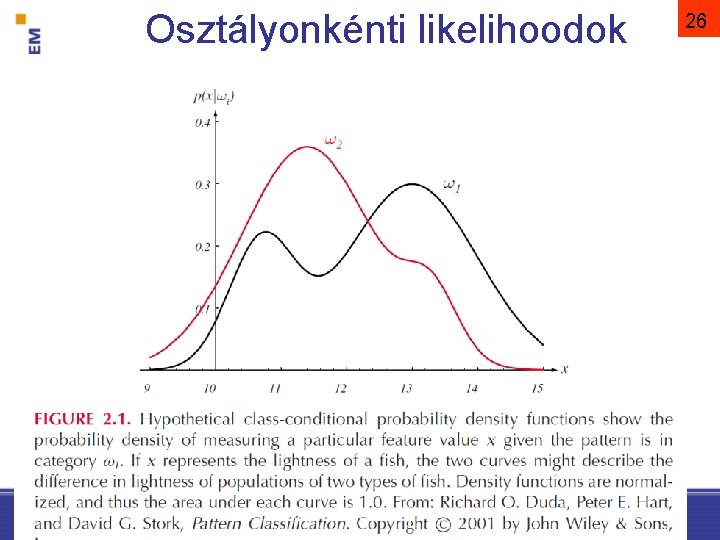
25 A posteriori valószínűség prior P( j | x) = P(x | j ) · P ( j ) / P(x) likelihood bizonyíték cél: P( j | x) modellezése Pattern Classification, Chapter 2 (Part 1)

Osztályonkénti likelihoodok 26

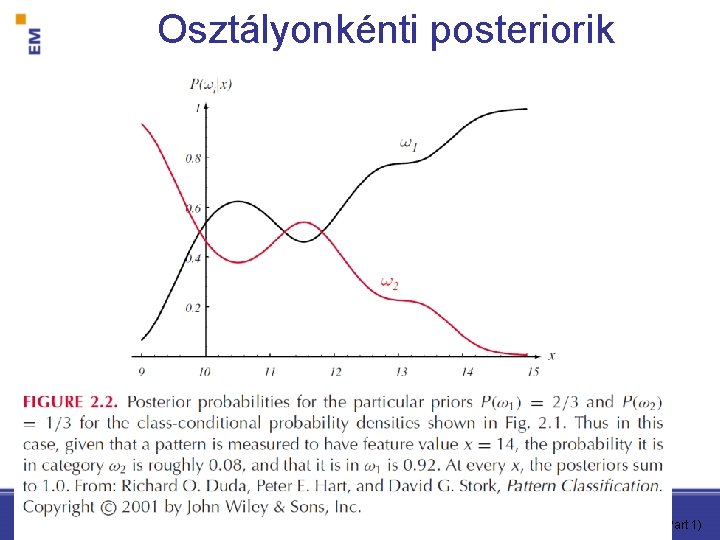
Osztályonkénti posteriorik Pattern Classification, Chapter 2 (Part 1)

28 Bayes osztályozó Ha x egy megfigyelés, amelyre: P( 1 | x) > P( 2 | x) P( 1 | x) < P( 2 | x) akkor a döntés 1 akkor a döntés 2 P(x | j ) és P ( j )-ket modellezük P(x) nem kell a döntéshez, ill.

A több osztályos osztályozó – általános eset 29 (nem csak Bayes döntéselmélet!) Diszkriminancia függvények halmaza: gi(x), i = 1, …, c – Az osztályozó egy x tulajdonságvektorhoz az i osztályt rendeli, ha: gi(x) = max gk(x) Pattern Classification, Chapter 2 (Part 1)

30 Két osztályos Bayes osztályozó egyetlen diszkriminancia fgv: döntés: g(x) > 0 Pattern Classification, Chapter 2 (Part 1)

Diszkriminancia-fügvények Bayes osztályozó és normális eloszlás esetén

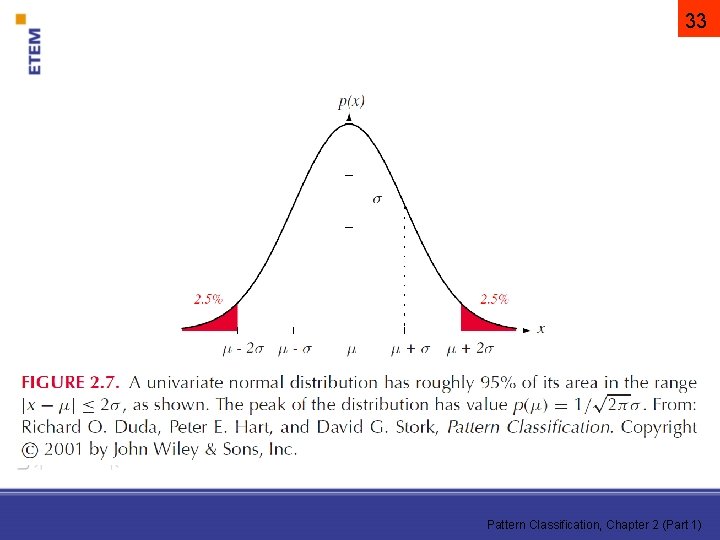
A normális eloszlás 32 • Egyváltozós eset – – Kezelhető sűrűségfüggvény Folytonos Nagyon sok valós eloszlás normális Centrális határeloszlás-tétele Ahol: = az X várható értéke 2 = szórásnégyzet (variancia) Pattern Classification, Chapter 2 (Part 1)

33 Pattern Classification, Chapter 2 (Part 1)

34 Többváltozós normális eloszlás • sűrűségfüggvénye ahol: x = (x 1, x 2, …, xd)t = ( 1, 2, …, d)t a várható érték vektor = d*d a kovariancia-mátrix | | illetve -1 a determináns illetve az inverz mátrix Pattern Classification, Chapter 2 (Part 1)

A normális eloszláshoz tartozó diszkriminancia függvények 35 gi(x) = ln P(x | I ) + ln P( I ) • Többváltozós normális eloszlásnál Pattern Classification, Chapter 2 (Part 1)

i = 36 2 I esete I az egységmátrix Pattern Classification, Chapter 2 (Part 1)

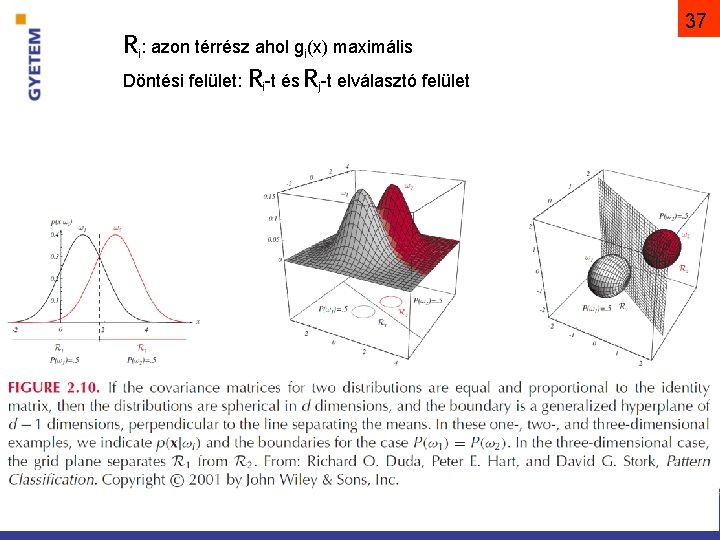
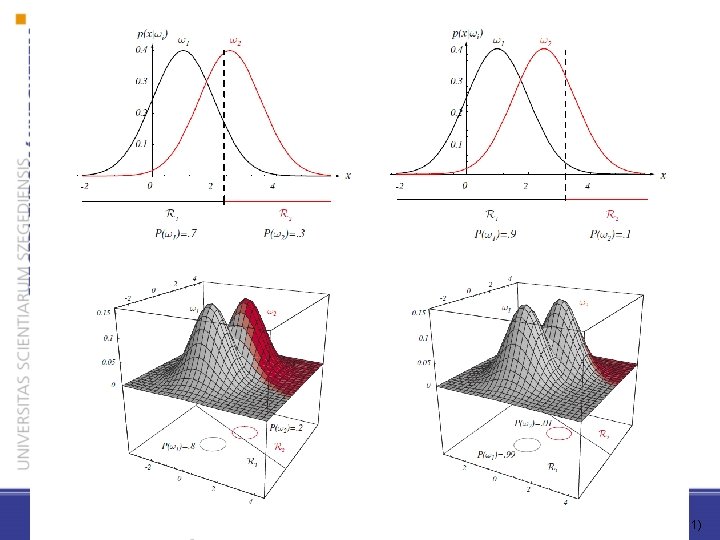
Ri: azon térrész ahol gi(x) maximális Döntési felület: Ri-t és Rj-t elválasztó felület 37 Pattern Classification, Chapter 2 (Part 1)

Pattern Classification, Chapter 2 (Part 1)

39 Pattern Classification, Chapter 2 (Part 1)

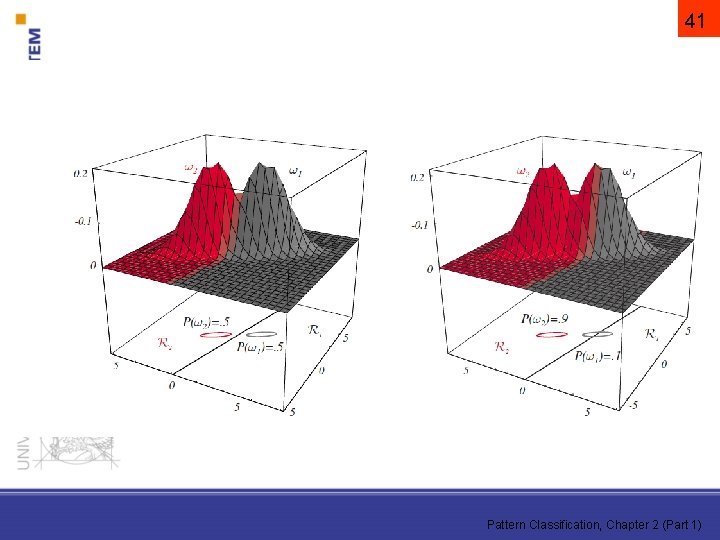
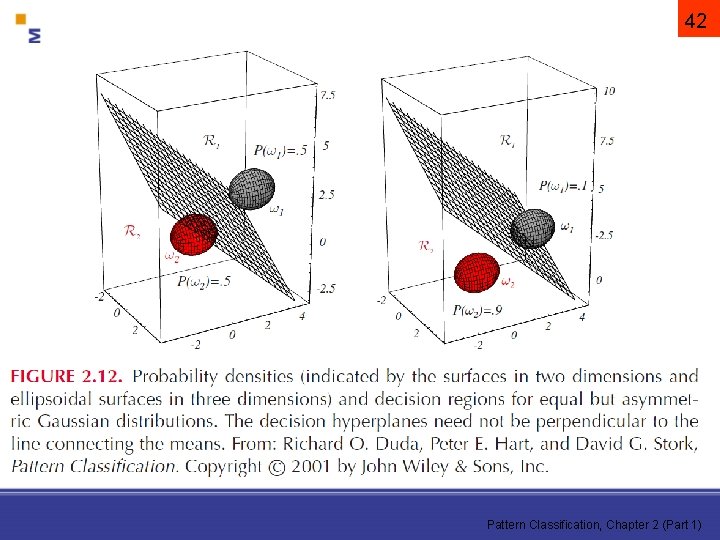
i = esete • a kovarianciamátrixok azonosak, de tetszőlegesek! Az Ri és Rj közti döntési felület hipersík, de általában nem merőleges a várható értékeket összekötő egyenesre!

41 Pattern Classification, Chapter 2 (Part 1)

42 Pattern Classification, Chapter 2 (Part 1)

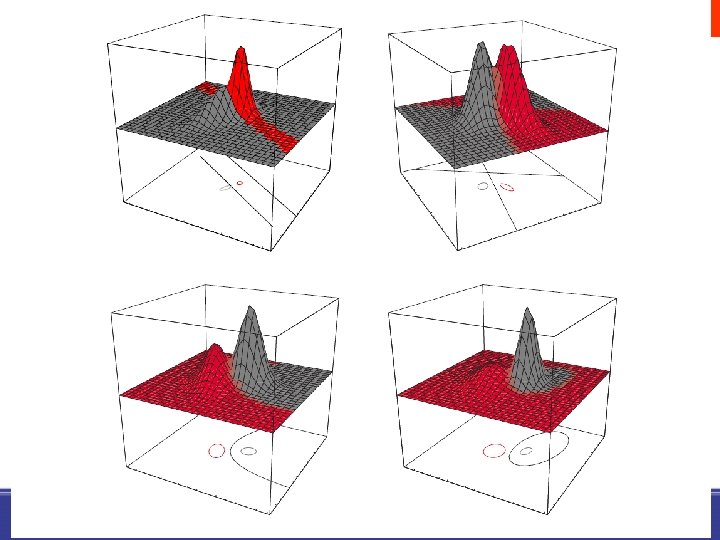
43 i tetszőleges • A kovarianciamátrixok minden osztálynál különbözőek (Hiperkvadratikusok: hipersíkok, hipersíkok párjai, hipergömbök, hiperellipszoidok, hiperparaboloidok, hiperboloidok) Pattern Classification, Chapter 2 (Part 1)


45 Pattern Classification, Chapter 2 (Part 1)

46 Pattern Classification, Chapter 2 (Part 1)


Eloszlások paramétereinek becslése Maximum-likelihood illetve Bayes-módszerrel

49 Osztályozó készítése tanítópéldákból – A Bayes döntési szabály • Optimális osztályozót tudnánk készíteni az alábbiak ismeretében: – P( i) – P(x | i) (a priori valószínűségek) (likelihood) Azonban a gyakorlatban ezek a legritkább esetben ismertek! – Általában csak példáink vannak • Az a priori eloszlás becslése nem okoz gondot • Az osztályonkénti eloszlás becslése nehéz! (magas dimenziószám, gyakran kevés példa) Pattern Classification, Chapter 3

50 Paraméteres tanulóalgoritmusok – A priori feltételezés a tanulandó eloszlásról: • Pl. feltételezzük, hogy P(x | i) ~ N( i, i) Így csak a 2 paramétert kell megbecsülni – Paraméterbecslési módszerek: • Maximum-Likelihood (ML) becslés, illetve Bayes-becslés • Hasonló eredményre vezetnek, de más elvi háttéren alapulnak • Bármelyiket válasszuk is, a kapott P(x| i) becslést ugyanúgy használjuk osztályozáskor Pattern Classification, Chapter 3

• Maximum likelihood becslés: – Feltételezi, hogy a paraméterek értéke rögzített, csak számunkra ismeretlen – Legjobb paraméterértéknek azt az értéket tekinti, ami legjobban magyarázza (max. valószínűséget rendeli) a tanítópéldákat • Bayes-becslés: – A paramétereket is valószínűségi változóként kezeli, így azok eloszlását keresi – Ehhez kiindul egy feltételezett a priori eloszlásból, melyet a tanítópéldák segítségével pontosít Pattern Classification, Chapter 3 51

52 Tanító adatbázis • Tanítópéldák – Tfh a D tanító-adatbázis n mintából áll: (x 1, 1), (x 2, 2), …, (xn, n) – „iid” feltevés: az elemek egymástól • függetlenek és • ugyanabból a megtanulandó eloszlásból származnak Pattern Classification, Chapter 3

53 A „likelihood” célfüggvény „maximum-likelihood” becslésén azt az értéket fogjuk érteni, amely maximizálja P(D | )-t “Az a érték, amely legjobban magyarázza az aktuálisan megfigyelt tanítópéldákat” – A „log-likelihood” célfüggvény l( ) = ln P(D | ) (optimuma ugyanott van, de egyszerűbb kezelni!) Pattern Classification, Chapter 3

54 Példa – Modellezési feltevések • Tfh. c osztályunk van, és mindegyik eloszlását egy-egy normális eloszlással közelítjük: P(x | j) ~ N( j, j) • A tanulandó paramétereket egy adott osztály esetén jelölje Pattern Classification, Chapter 3

55 A (log-)likelihood maximalizálása • Keressük azt a -t, amely maximalizálja az l( ) log-likelihood-ot:

56 A (log-)likelihood maximalizálása Az optimumhelyhez szükséges feltétel: (p az ismeretlen paraméterek száma) l = 0 (megj: esetünkben a vizsgált függvények jellege miatt elégséges is lesz) Pattern Classification, Chapter 3

57 Példa: egyváltozós Gauss-eloszlás, és ismeretlen azaz = ( 1, 2) = ( , 2) Pattern Classification, Chapter 3

58 Az összes példára összegezve: Kombinálva (1)-et és (2)-t, azt kapjuk hogy: Pattern Classification, Chapter 3

59 Bayes becslés – -t is valószínűségi változóként kezeli, nem pedig rögzített de ismeretlen paraméterként – A P( ) kezdeti eloszlását a priori tudásként ismertnek tekintjük – A D tanítópéldák alapján keressük P( | D)-t – Majd ennek segítségével írjuk fel P(x | D)-t Pattern Classification, Chapter 3

60 Bayes becslés Az alapvető feltevések: • P(x | ) formája ismert • -ra vonatkozó ismereteink P( ) ismeretének formájában állnak rendelkezésre • Összes többi -ra vonatkozó ismeretünket n db P(x) -ből származó D={ x 1, x 2, …, xn } minta tartalmazza Pattern Classification, Chapter 3

61 A Bayes becslés két lépése 1. P( | D) levezetése Bayes-szabály, illetve a függetlenségi feltevés kell: 2. P(x | D) levezetése Megj. : ez sokszor nem vezethető le zárt képlettel, ezért közelítjük vagy zárt alakban vagy numerikusan (pl. Gibbs algorithm) Pattern Classification, Chapter 3

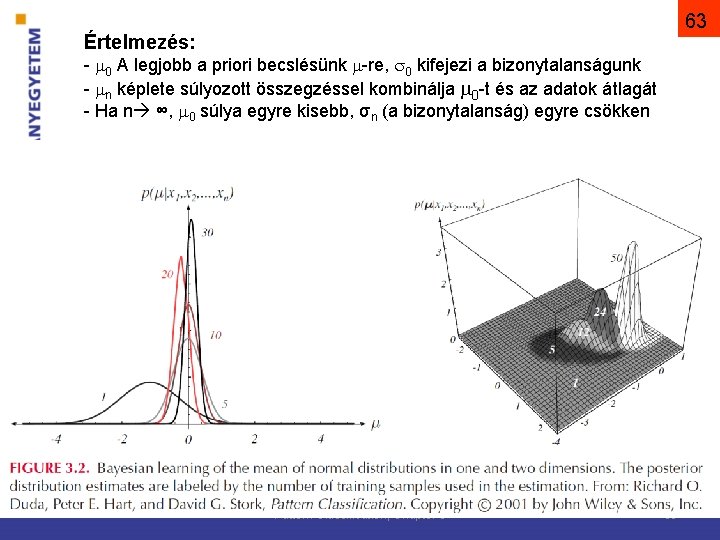
62 Bayes becslés - Példa P(x| ) egyváltozós Gauss-eloszlás, ismert, csak -t keressük amit keresünk, az ismeretlen paraméter(eloszlás): Tobábbá -nek ismert az a priori eloszlása: Pattern Classification, Chapter 3

63 Értelmezés: - 0 A legjobb a priori becslésünk -re, 0 kifejezi a bizonytalanságunk - n képlete súlyozott összegzéssel kombinálja 0 -t és az adatok átlagát - Ha n ∞, 0 súlya egyre kisebb, σn (a bizonytalanság) egyre csökken Pattern Classification, Chapter 3 63

Példa – P( | D) levezetése feltesszük: … Pattern Classification, Chapter 3 64

Példa – P(x | D) kiszámítása • P( | D) megvan, P(x | D) még kiszámítandó! Levezethető, hogy P(x | D) normális eloszlás az alábbi paraméterekkel: Tehát n lesz a várható érték, σ-hoz pedig hozzáadódik σn, kifejezve a -re vonatkozó bizonytalanságot Többváltozós eset: Pattern Classification, Chapter 3 65

66 MLE vs. Bayes becslés • Ha n→∞ akkor megegyeznek! • maximum-likelihood becslés – egyszerű, gyors(abb) /grádiens keresés vs. multidim. integrálás/ • Bayes becslés – ha a feltevéseink bizonytalanok – bizonytalanságot a P( )-val modellezhetjük

Összefoglalás • Bayes osztályozó ismert (normális) eloszlások mellett • Paraméterbecslések Általános módszer paraméteres eloszlások paramétereinek becslésére egy minta alapján (nem csak Bayes!)
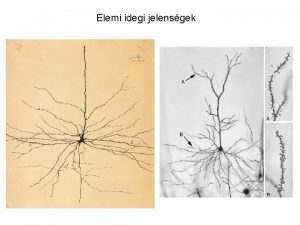
 Elemi rost
Elemi rost Na k pumpa
Na k pumpa Elemi karbon
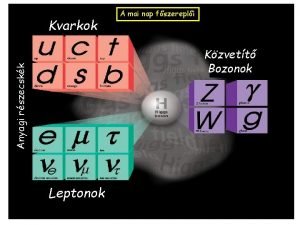
Elemi karbon Kvarkok
Kvarkok Mrc scala forza
Mrc scala forza Mmrc escala
Mmrc escala Mrc grade
Mrc grade Deepa tailor
Deepa tailor Trc mrc root cause
Trc mrc root cause Escala de disnea
Escala de disnea Echelle de sadoul
Echelle de sadoul Mrc oulu
Mrc oulu Tone of muscle examination
Tone of muscle examination Mrc clinical trials unit
Mrc clinical trials unit Mrc dyspnoea scale
Mrc dyspnoea scale Hepatojuguler reflü muayenesi
Hepatojuguler reflü muayenesi Mrc modificada
Mrc modificada Fairfax mrc
Fairfax mrc Mrc clinical research training fellowship
Mrc clinical research training fellowship Respuesta de decorticacion
Respuesta de decorticacion Mrc dyspnoea scale
Mrc dyspnoea scale Kobkoonka
Kobkoonka Modified mrc scale
Modified mrc scale Mrc scale
Mrc scale Esztergálás alapjai
Esztergálás alapjai Bérszámfejtés menete
Bérszámfejtés menete Dresszírozás
Dresszírozás Táblázatkezelés alapjai
Táblázatkezelés alapjai Html alapjai
Html alapjai Az immunológia alapjai pdf
Az immunológia alapjai pdf Turisztikai termékek csoportosítása
Turisztikai termékek csoportosítása Co2 hegesztés alapjai
Co2 hegesztés alapjai Fuvarszervezés alapjai
Fuvarszervezés alapjai Rendezvény forgatókönyv minta
Rendezvény forgatókönyv minta Beszúrás kés
Beszúrás kés Gyökér irén menedzsment alapjai
Gyökér irén menedzsment alapjai Informatikai biztonság alapjai
Informatikai biztonság alapjai Kraljic mátrix fogalma
Kraljic mátrix fogalma Kontírozás alapjai
Kontírozás alapjai Elektronika alapjai
Elektronika alapjai Webprogramozás alapjai
Webprogramozás alapjai Diszjunktív sorszámos alak
Diszjunktív sorszámos alak Repülés fizikai alapjai
Repülés fizikai alapjai Számlaosztályok 1-9
Számlaosztályok 1-9 Cnc programozás alapjai
Cnc programozás alapjai Tömegspektrometria alapjai
Tömegspektrometria alapjai Bérszámfejtés alapjai
Bérszámfejtés alapjai Elektrokardiográfia
Elektrokardiográfia