UNIT 1 QUADRATICS REVISITED Test 817 LG 1






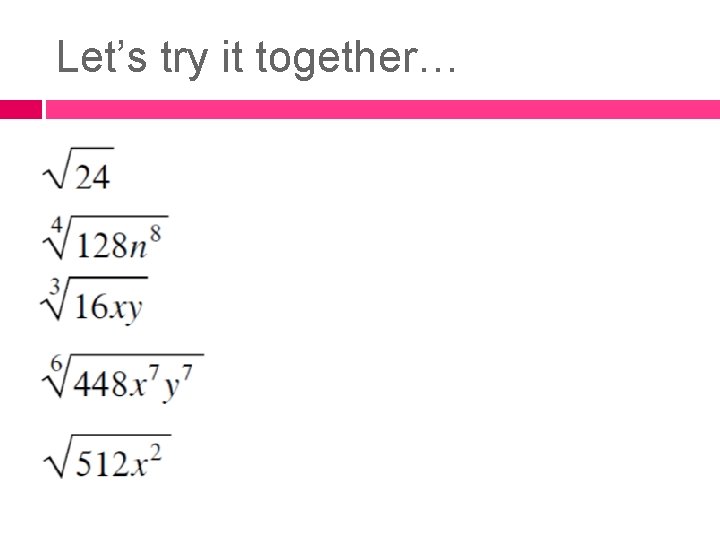



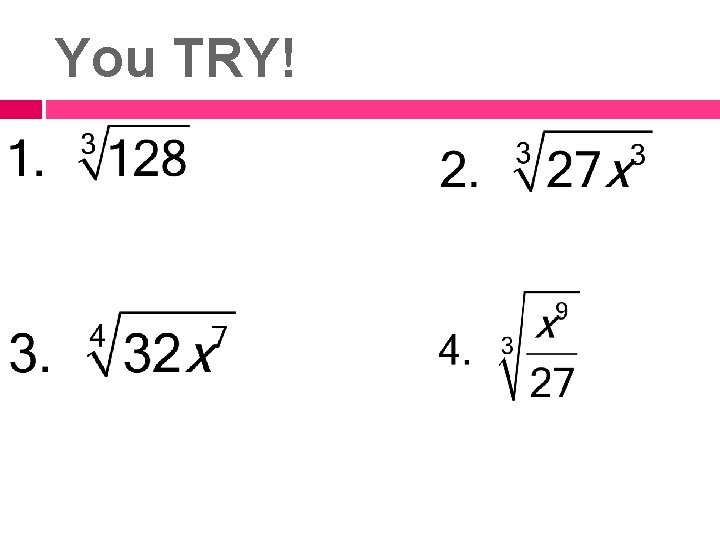
















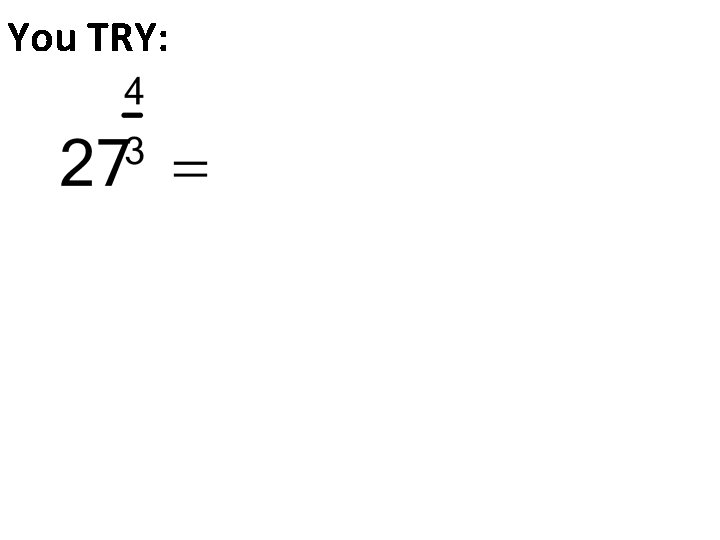
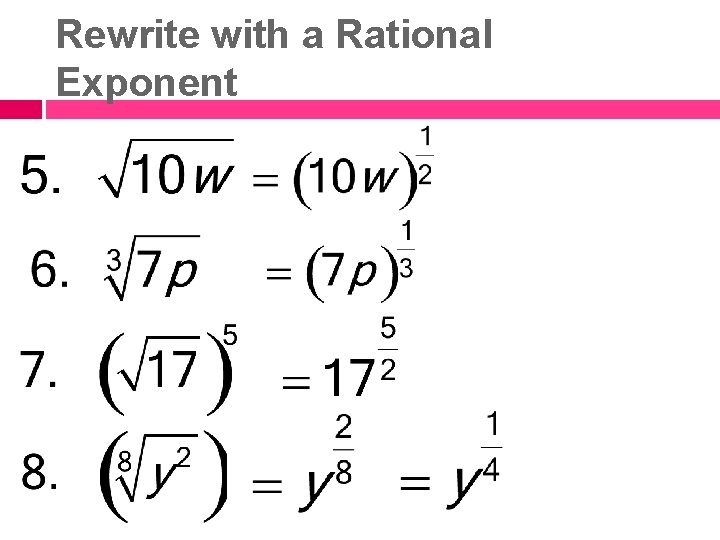
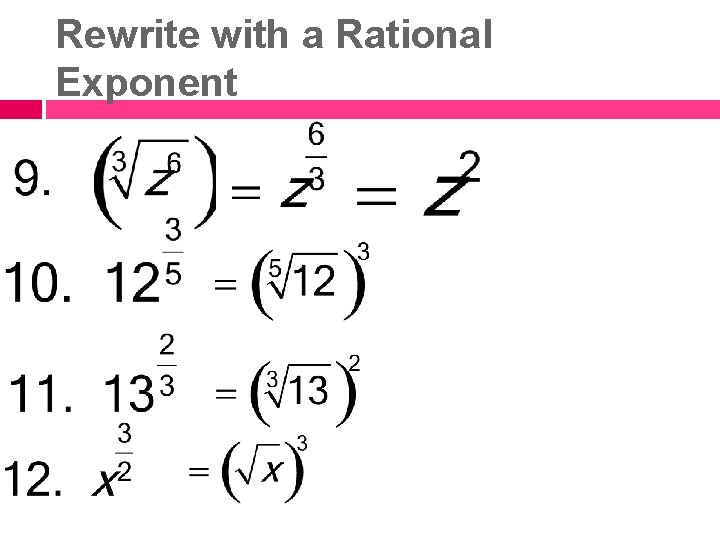

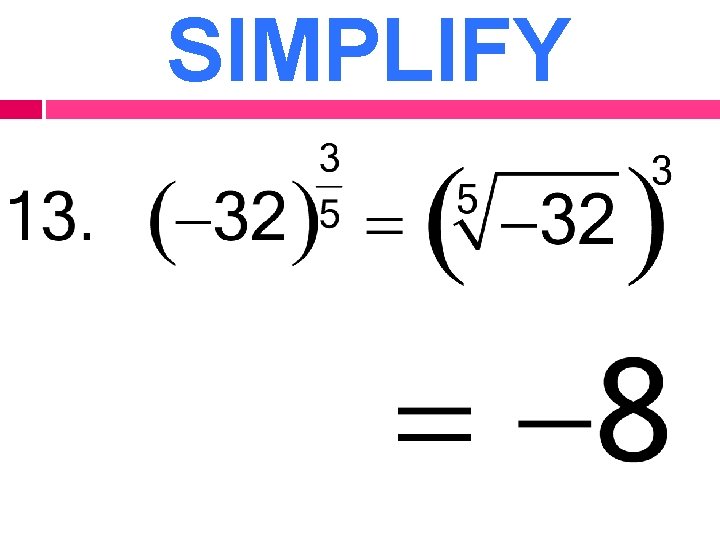
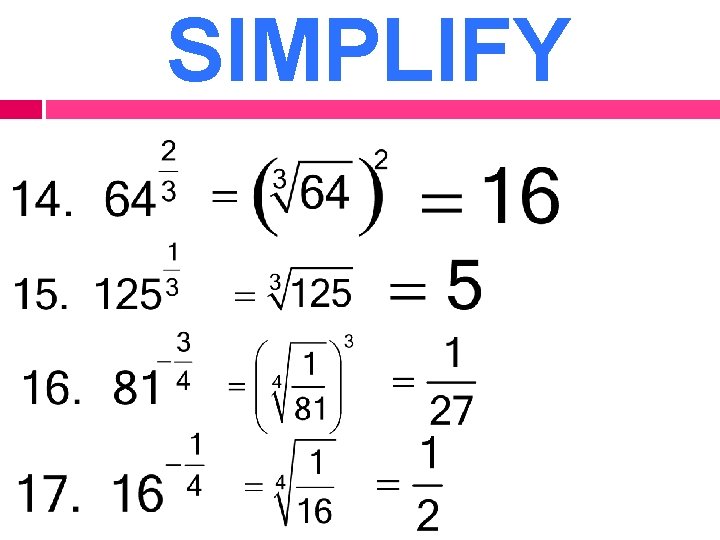


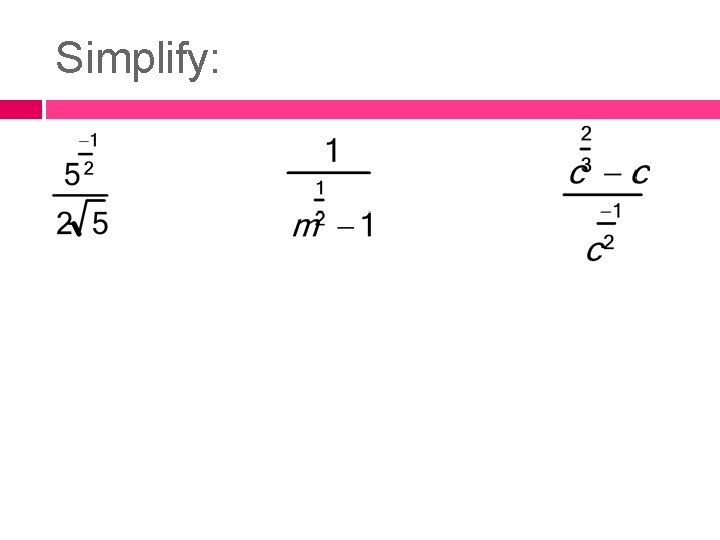









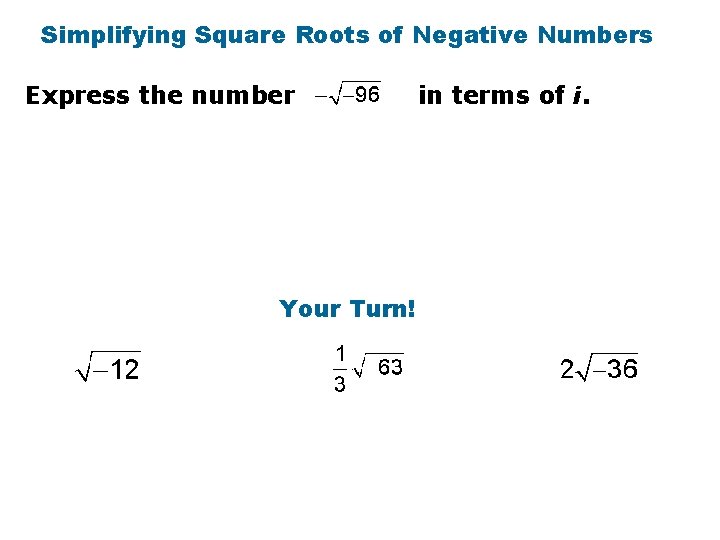




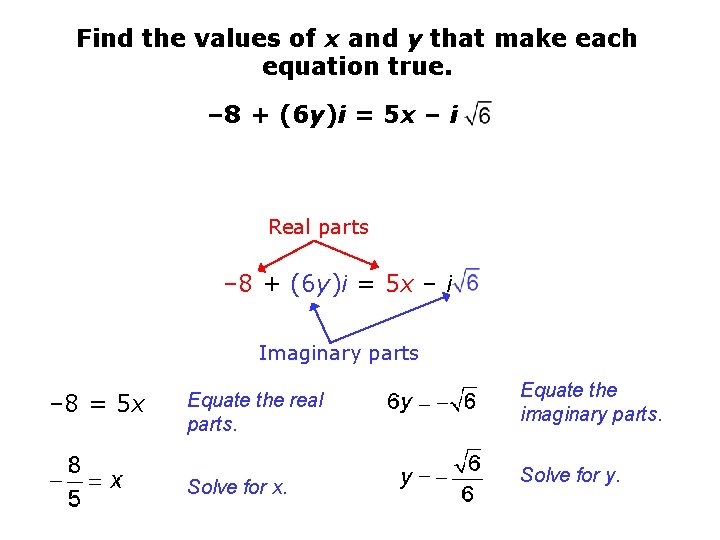
















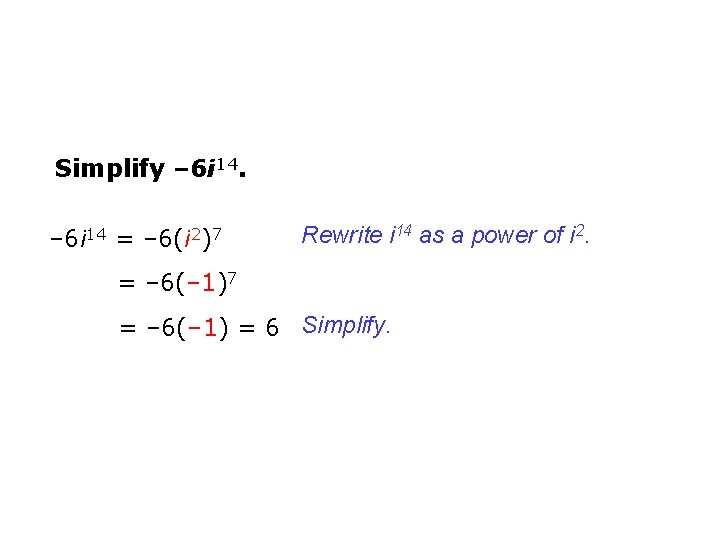






















- Slides: 103

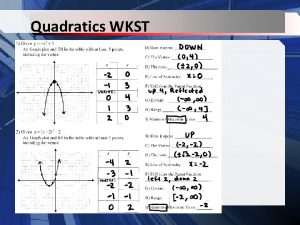
UNIT 1: QUADRATICS REVISITED Test 8/17

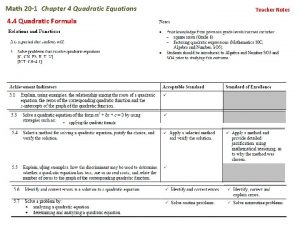
LG 1 -1 Nth Roots & Rational Exponents Extend the properties of exponents to rational exponents � MGSE 9 -12. N. RN. 1. Explain how the meaning of rational exponents follows from extending the properties of integer exponents to rational numbers, allowing for a notation for radicals in terms of rational exponents. MGSE 9 -12. N. RN. 2 Rewrite expressions involving radicals and rational exponents using the properties of exponents.

ENDURING UNDERSTANDINGS Nth roots are inverses of power functions (like x squared, x cubed, etc). Understanding the properties of power functions and how inverses behave explains the properties of nth roots. Real-life situations are rarely modeled accurately using discrete data. It is often necessary to introduce rational exponents to model and make sense of a situation. Computing with rational exponents is no different from computing with integer exponents.

ESSENTIAL QUESTIONS How are rational exponents and roots of expressions similar?

EVIDENCE OF LEARNING By the conclusion of this learning goal, you should be able to Make connections between radicals and fractional exponents Results of operations performed between numbers from a particular number set does not always belong to the same set.

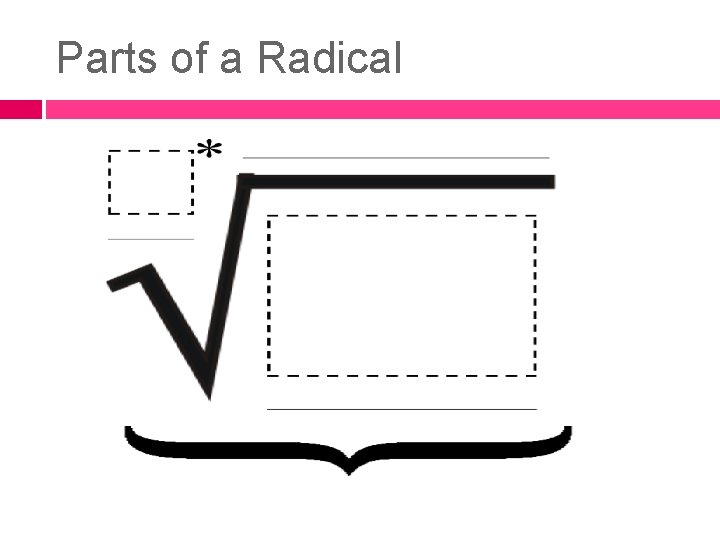
Parts of a Radical

Simplifying Radicals When simplifying radicals, you must know the perfect squares. Break down the radicand in to prime factors. Bring out groups by the number of the index/root.
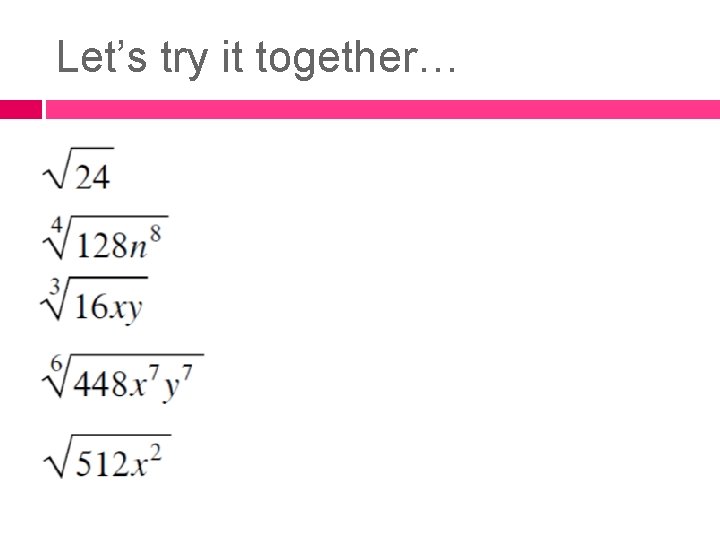
Let’s try it together…

Let’s try it together…

Steps for Simplifying Radicals 1. 2. 3. 4. 5. 6. Write the prime factorization of your radicand. Determine the index of the radical. If the index is 2, circle groups of 2 identical numbers or variables. If the index is 3, circle groups of 3 identical numbers or variables, etc. The number or variable from each circled group will show up outside the radical symbol 1 time. Anything left uncircled will remain under the radical. If everything under the radical symbol is circled, the radical symbol will disappear. Multiply the numbers and variables outside the radical together.

TI – 36 X Pro Prime Factors for YOU 1. Type in the number you need to prime factor 2. Press math 3. Scroll down to the 4 th one Pfactor and enter (or just press math 4)
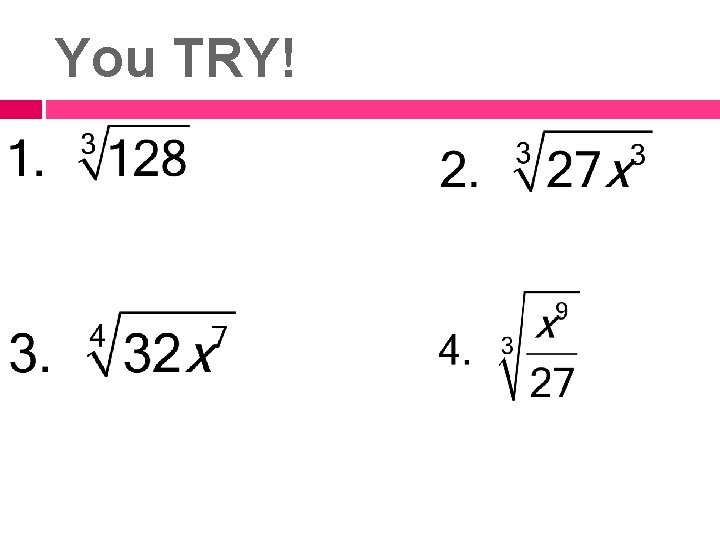
You TRY!

Practice Sheet Adding / Subtracting Radicals � Make sure the radicals are in simplest form before you add or subtract. � In order to add or subtract radicals, the number inside the radicals must be the exactly the same. � When the radicands are the same, then, you can add or subtract only the numbers in front of the radicals � The radicands are treated kind of like variables.

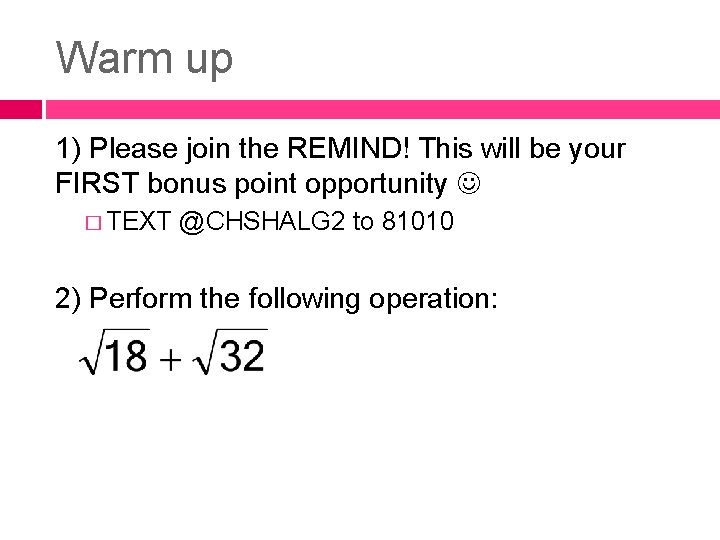
Warm up 1) Please join the REMIND! This will be your FIRST bonus point opportunity � TEXT @CHSHALG 2 to 81010 2) Perform the following operation:

Operating with Radicals Sometimes we need to simplify more that one radical in order to be able to add or subtract them. We need to simplify both terms to see if we have the same radicands!!!

Operating with Radicals

YOU TRY!

Rationalizing the Denominator It is sometimes easier to work with radical expressions if the denominators do not contain any radicals. The process of rewriting a radical expression as an equivalent rational expression with no radicals in the denominator is called rationalizing the denominator.

Rationalize the Denominator:

Rationalizing the Denominator If the denominator has two terms with one or more square roots, we can rationalize the denominator by multiplying the numerator and denominator by the conjugate of the denominator. A + B and A – B are conjugates. The product (A + B)(A – B) = A 2 – B 2

Rationalizing a Binomial Denominator Examples: Rationalize the denominator of

Rationalizing Denominators

Rationalizing Denominators If the denominator is a single radical term with nth root: � See what expression you would need to multiply by to obtain a perfect nth power in the denominator. Multiply numerator and denominator by that expression. If the denominator contains two terms involving square roots: � Rationalize the denominator by multiplying the numerator and the denominator by the conjugate of the denominator.

In Summary… Radical expressions that involve the sum and difference of the same two terms are called conjugates. The process of rewriting a radical expression as an equivalent expression without any radicals in the denominator is called rationalizing the denominator. GET THOSE RADICALS OUT OF THE DENOMINATOR!!!!

Classwork/Homework

Warm up!

REWRITING A RADICAL TO HAVE A RATIONAL EXPONENT

Rewriting Radicals to Rational Exponents Power is on top Roots are in the ground

There are 3 different ways to write a rational exponent:
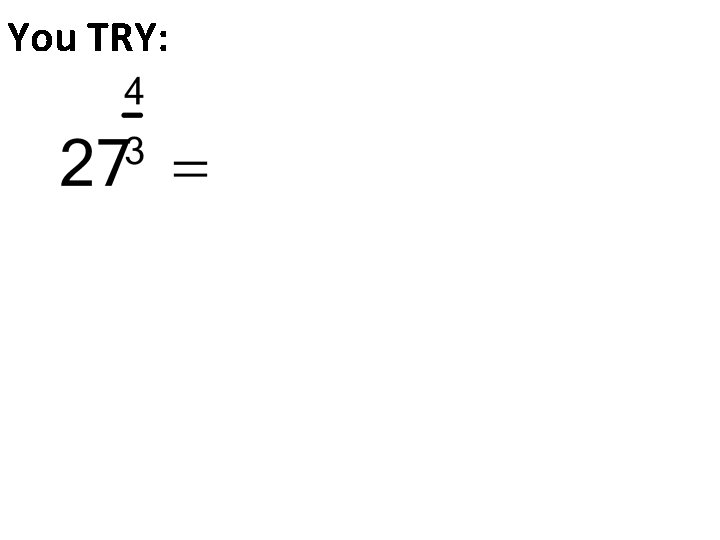
You TRY:
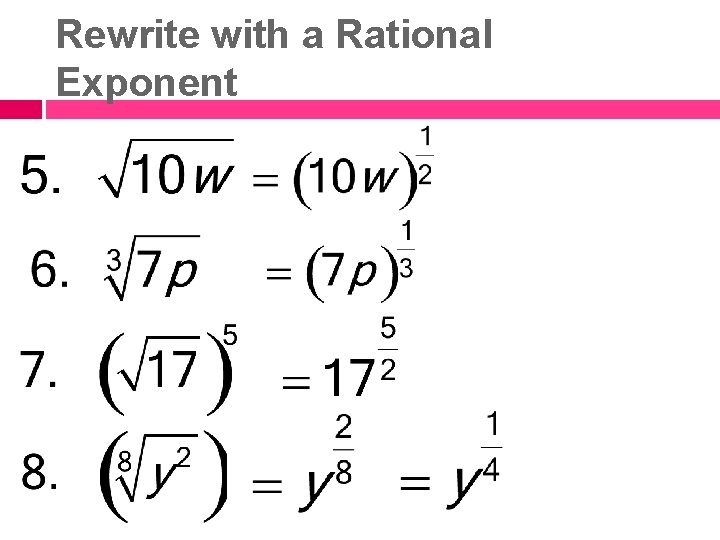
Rewrite with a Rational Exponent
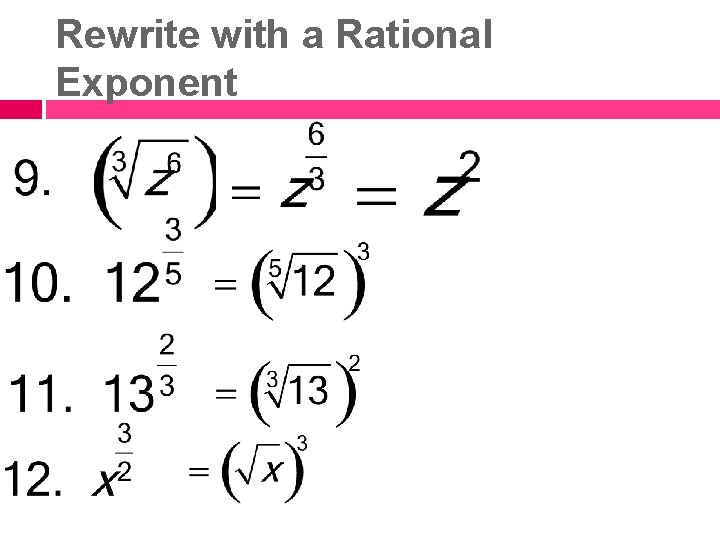
Rewrite with a Rational Exponent

SIMPLIFY Sometimes you can simplify in the calculator. KNOW how to do it by hand!! Change to a radical Prime Factor Bring out groups of the root
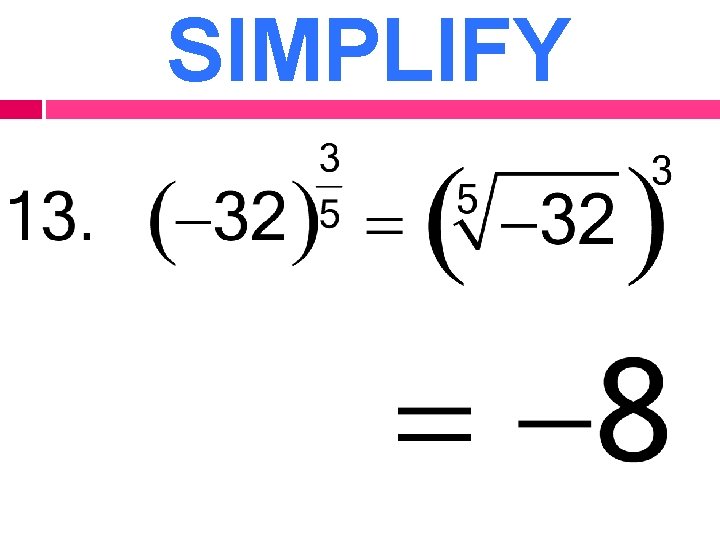
SIMPLIFY
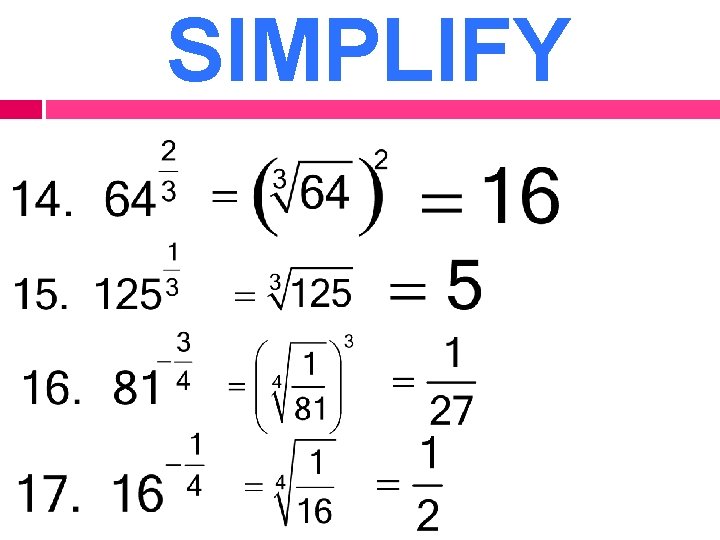
SIMPLIFY

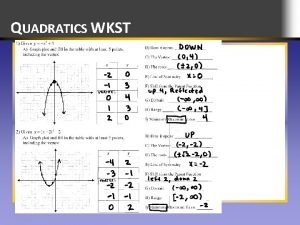
WARM UP Simplify each expression completely:

Simplifying Expressions No negative exponents No fractional exponents in the denominator No complex fractions (fraction within a fraction) The index of any remaining radical is the least possible number
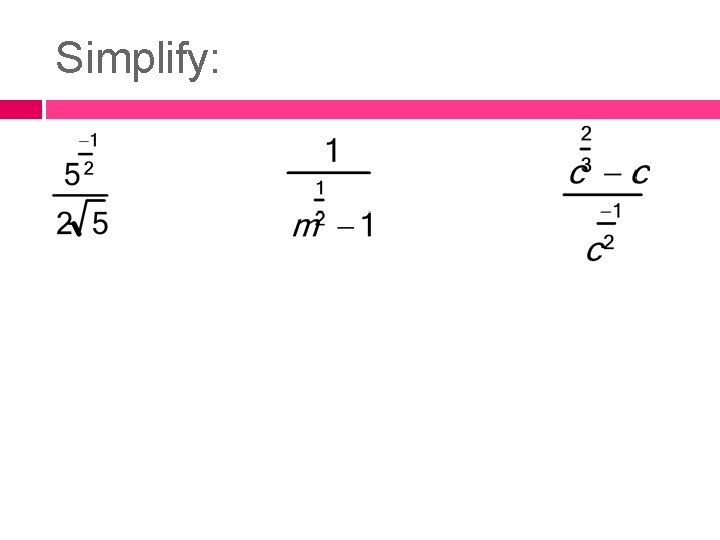
Simplify:

Practice Continue to work on this concept

Warm UP
Exponent survey

Higher order roots practice

Warm up Simplify each expression.

QUEEEEEEZ TIME! You have 20 minutes to finish the quiz. When you have selected your answers, raise your hand I will check your answers. If I fold your paper in half, you have earned 100% on the quiz. Congrats! If you missed any questions, I will tell you the number of questions you missed. The number I give you does not correspond to the question number. It is now YOUR job to find the incorrect answer(s) and fix it(them). Once you feel you have made corrections, raise your hand I will check again. At this point, it is STILL POSSIBLE to make 100% on the quiz! If I now take and fold your paper, you also have earned 100%! If I tell you another number then you get one more chance to fix your error before I collect the quiz and grade it as is. GOOD LUCK!

LG 1 -2 Complex Numbers • Define and use imaginary and complex numbers. • Solve quadratic equations with complex roots.

Why do we need them? You can see in the graph of the parabola below that it does not touch the x-axis. This means it has no real zeros. If you solve the equation 0 = x 2 + 1, you find that x = which has no real solutions. However, you can find solutions if you define the square root of negative numbers, which is why imaginary numbers were invented. The imaginary unit i is defined as . You can use the imaginary unit to write the square root of any negative number.


Simplifying Square Roots of Negative Numbers Express the number in terms of i. Factor out – 1. Product Property. Simplify. Multiply. Express in terms of i.
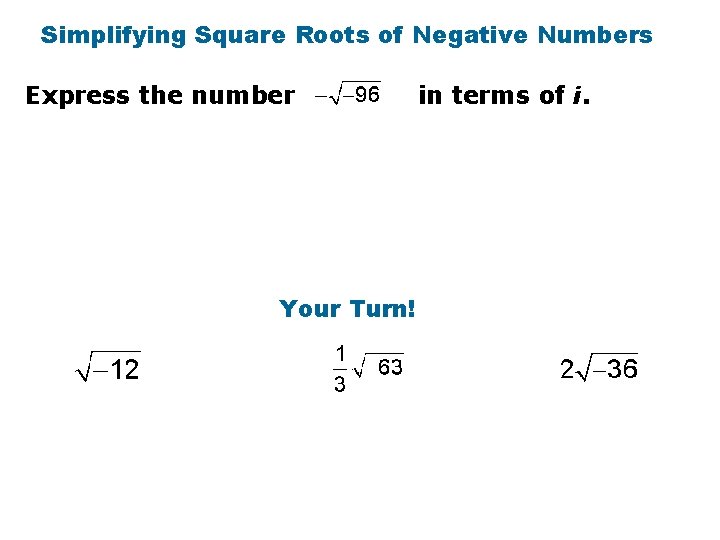
Simplifying Square Roots of Negative Numbers Express the number Your Turn! in terms of i.

Complex Numbers A complex number is a number that can be written in the form a + bi, where a and b are real numbers and i=. The set of real numbers is a subset of the set of complex numbers C. Every complex number has a real part a and an imaginary part b.

Complex Numbers Real numbers are complex numbers where b = 0. Imaginary numbers are complex numbers where a = 0 and b ≠ 0. These are sometimes called pure imaginary numbers. Two complex numbers are equal if and only if their real parts are equal and their imaginary parts are equal.

Equating Two Complex Numbers Find the values of x and y that make the equation 4 x + 10 i = 2 – (4 y)i true. Real parts 4 x + 10 i = 2 – (4 y)i Imaginary parts 4 x = 2 Equate the real parts. Solve for x. 10 = – 4 y Equate the imaginary parts. Solve for y.

Find the values of x and y that make each equation true. 2 x – 6 i = – 8 + (20 y)i Real parts 2 x – 6 i = – 8 + (20 y)i Imaginary parts 2 x = – 8 Equate the real parts. x = – 4 Solve for x. – 6 = 20 y Equate the imaginary parts. Solve for y.
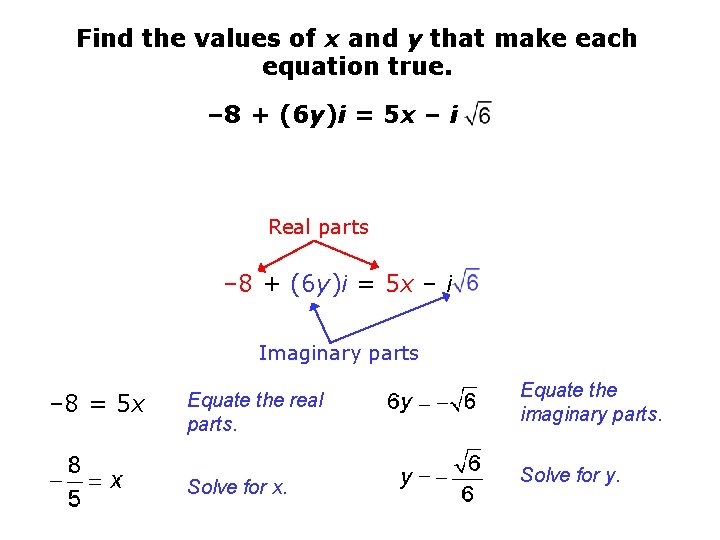
Find the values of x and y that make each equation true. – 8 + (6 y)i = 5 x – i Real parts – 8 + (6 y)i = 5 x – i Imaginary parts – 8 = 5 x Equate the real parts. Solve for x. Equate the imaginary parts. Solve for y.

Solve the following Quadratic Equation: g(x) = x 2 – 8 x + 18

Other operations with complex numbers Adding and subtracting complex numbers is similar to adding and subtracting variable expressions with like terms. Simply combine the real parts, and combine the imaginary parts. The set of complex numbers has all the properties of the set of real numbers. So you can use the Commutative, Associative, and Distributive Properties to simplify complex number expressions.

Adding and Subtracting Complex Numbers Add or subtract. Write the result in the form a + bi. (4 + 2 i) + (– 6 – 7 i) (4 – 6) + (2 i – 7 i) – 2 – 5 i Add real parts and imaginary parts.

Adding and Subtracting Complex Numbers Add or subtract. Write the result in the form a + bi. (5 – 2 i) – (– 2 – 3 i) (5 – 2 i) + 2 + 3 i Distribute. (5 + 2) + (– 2 i + 3 i) Add real parts and imaginary parts. 7+i

Adding and Subtracting Complex Numbers Add or subtract. Write the result in the form a + bi. (1 – 3 i) + (– 1 + 3 i) (1 – 1) + (– 3 i + 3 i) 0 Add real parts and imaginary parts.

Add or subtract. Write the result in the form a + bi. (– 3 + 5 i) + (– 6 i) (– 3) + (5 i – 6 i) – 3 – i Add real parts and imaginary parts.

Add or subtract. Write the result in the form a + bi. 2 i – (3 + 5 i) (2 i) – 3 – 5 i Distribute. (– 3) + (2 i – 5 i) Add real parts and imaginary parts. – 3 i

Add or subtract. Write the result in the form a + bi. (4 + 3 i) + (4 – 3 i) (4 + 4) + (3 i – 3 i) 8 Add real parts and imaginary parts.

Multiplying Complex Numbers You can multiply complex numbers by using the Distributive Property and treating the imaginary parts as like terms. Simplify by using the fact i 2 = – 1. Multiply. Write the result in the form a + bi. – 2 i(2 – 4 i) – 4 i + 8 i 2 Distribute. – 4 i + 8(– 1) Use i 2 = – 1. – 8 – 4 i Write in a + bi form.

Multiply. Write the result in the form a + bi. (3 + 6 i)(4 – i) 12 + 24 i – 3 i – 6 i 2 Multiply. 12 + 21 i – 6(– 1) Use i 2 = – 1. 18 + 21 i Write in a + bi form.

Multiply. Write the result in the form a + bi. (2 + 9 i)(2 – 9 i) 4 – 18 i + 18 i – 81 i 2 Multiply. 4 – 81(– 1) Use i 2 = – 1. 85 Write in a + bi form.

Multiply. Write the result in the form a + bi. (– 5 i)(6 i) – 30 i 2 Multiply. – 30(– 1) Use i 2 = – 1 30 Write in a + bi form.

Multiply. Write the result in the form a + bi. 2 i(3 – 5 i) 6 i – 10 i 2 Distribute. 6 i – 10(– 1) Use i 2 = – 1. 10 + 6 i Write in a + bi form.

Multiply. Write the result in the form a + bi. (4 – 4 i)(6 – i) 24 – 4 i – 24 i + 4 i 2 Distribute. 24 – 28 i + 4(– 1) Use i 2 = – 1. 20 – 28 i Write in a + bi form.

Multiply. Write the result in the form a + bi. (3 + 2 i)(3 – 2 i) 9 + 6 i – 4 i 2 Distribute. 9 – 4(– 1) Use i 2 = – 1. 13 Write in a + bi form.

The imaginary unit i can be raised to higher powers as shown below. Helpful Hint Notice the repeating pattern in each row of the table. The pattern allows you to express any power of i as one of four possible values: i, – 1, –i, or 1.
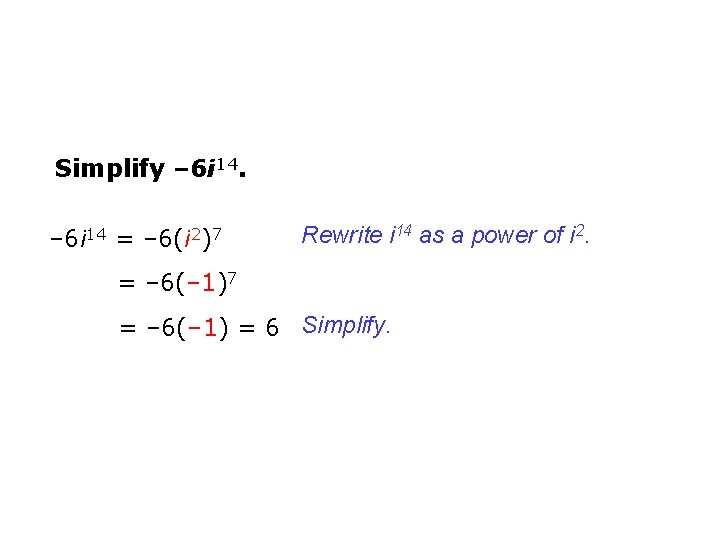
Simplify – 6 i 14 = – 6(i 2)7 Rewrite i 14 as a power of i 2. = – 6(– 1)7 = – 6(– 1) = 6 Simplify.

Simplify i 63 = i i 62 = i (i 2)31 Rewrite as a product of i and an even power of i. Rewrite i 62 as a power of i 2. = i (– 1)31 = i – 1 = –i Simplify.

Simplify . Rewrite as a product of i and an even power of i. Rewrite i 6 as a power of i 2. Simplify.

Simplify i 42 = ( i 2)21 = (– 1)21 = – 1 Rewrite i 42 as a power of i 2. Simplify.

Warm Up Express each number in terms of i. 1. 9 i 2. Find each complex conjugate. 3. 4. Find each product. 5. 6.

Today’s Objective: Perform operations with complex numbers. Just as you can represent real numbers graphically as points on a number line, you can represent complex numbers in a special coordinate plane. The complex plane is a set of coordinate axes in which the horizontal axis represents real numbers and the vertical axis represents imaginary numbers.

Complex Conjugates The solutions and are related. These solutions are a complex conjugate pair. Their real parts are equal and their imaginary parts are opposites. The complex conjugate of any complex number a + bi is the complex number a – bi. Helpful Hint When given one complex root, you can always find the other by finding its conjugate.

Finding Complex Zeros of Quadratic Functions Find each complex conjugate. B. 6 i A. 8 + 5 i 8 – 5 i Write as a + bi. Find a – bi. 0 + 6 i 0 – 6 i Write as a + bi. Find a – bi. Simplify.

Find each complex conjugate. B. A. 9 – i 9 + (–i) Write as a + bi. 9 – (–i) 9+i Find a – bi. C. – 8 i 0 + (– 8)i 0 – (– 8)i 8 i Simplify. Write as a + bi. Find a – bi. Simplify.

Lesson Check In 1. Express in terms of i. Solve each equation. 2. 3 x 2 + 96 = 0 3. x 2 + 8 x +20 = 0 4. Find the values of x and y that make the equation 3 x +8 i = 12 – (12 y)i true. 5. Find the complex conjugate of

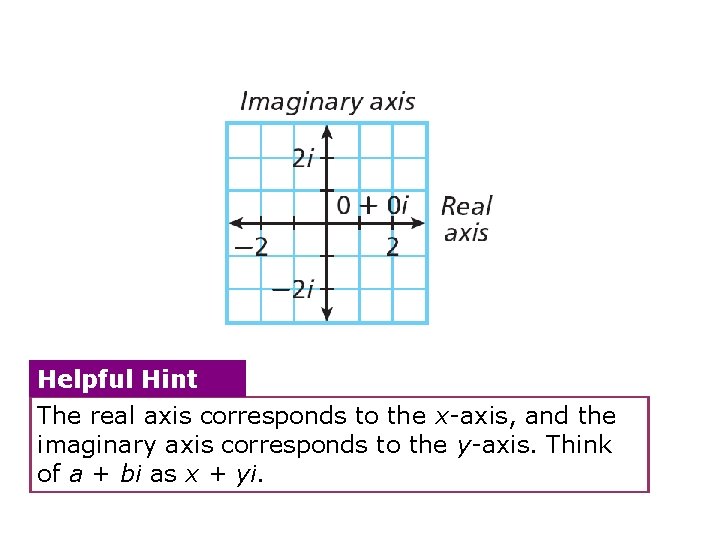
Helpful Hint The real axis corresponds to the x-axis, and the imaginary axis corresponds to the y-axis. Think of a + bi as x + yi.

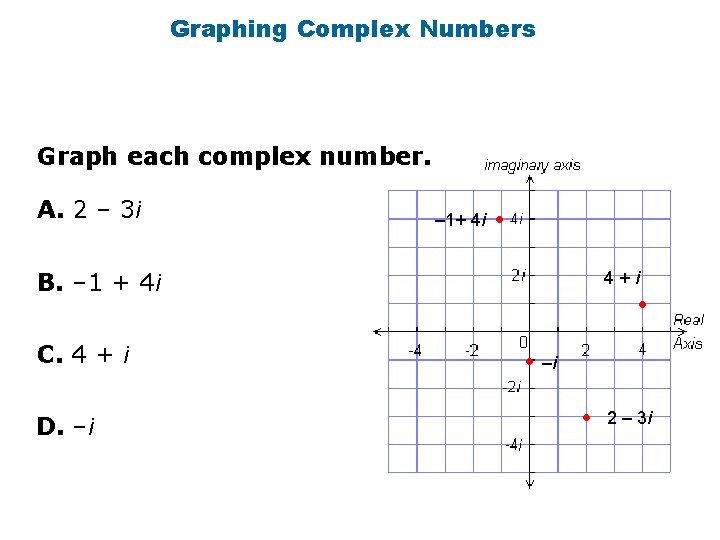
Graphing Complex Numbers Graph each complex number. A. 2 – 3 i – 1+ 4 i • B. – 1 + 4 i C. 4 + i D. –i 4+i • • –i • 2 – 3 i

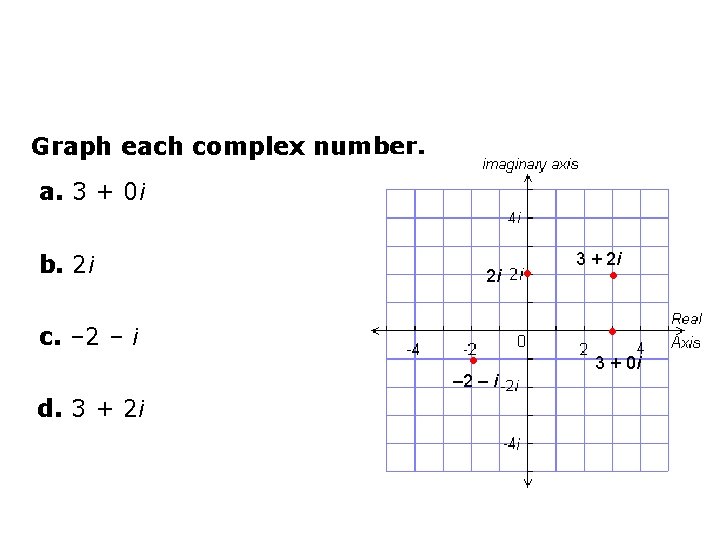
Graph each complex number. a. 3 + 0 i b. 2 i c. – 2 – i 2 i • – 2 – i d. 3 + 2 i • • 3 + 0 i

Absolute Value of a Complex Number Recall that absolute value of a real number is its distance from 0 on the real axis, which is also a number line. Similarly, the absolute value of an imaginary number is its distance from 0 along the imaginary axis.

Determining the Absolute Value of Complex Numbers Find each absolute value. A. |3 + 5 i| B. |– 13| C. |– 7 i| |– 13 + 0 i| |0 +(– 7)i| 13 7

Find each absolute value. a. |1 – 2 i| b. c. |23 i| |0 + 23 i| 23

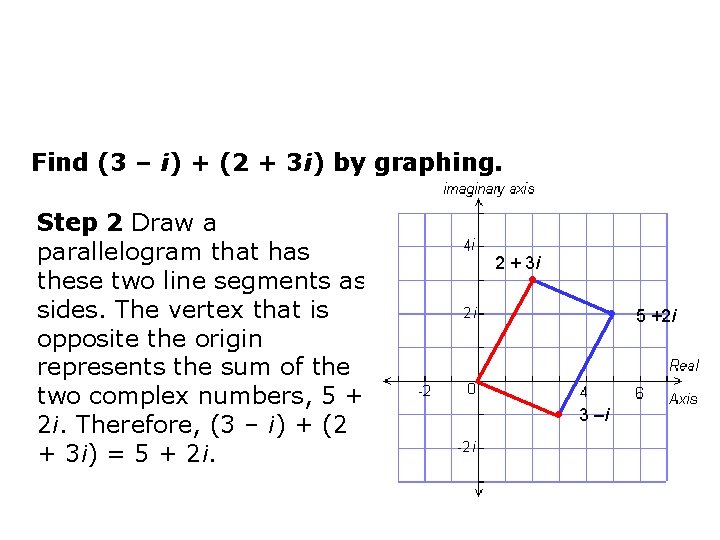
Adding Complex Numbers on the Complex Plane You can also add complex numbers by using coordinate geometry. Find (3 – i) + (2 + 3 i) by graphing. Step 1 Graph 3 – i and 2 + 3 i on the complex plane. Connect each of these numbers to the origin with a line segment. 2 + 3 i • • 3 –i

Find (3 – i) + (2 + 3 i) by graphing. Step 2 Draw a parallelogram that has these two line segments as sides. The vertex that is opposite the origin represents the sum of the two complex numbers, 5 + 2 i. Therefore, (3 – i) + (2 + 3 i) = 5 + 2 i. 2 + 3 i • • • 3 –i 5 +2 i

Find (3 – i) + (2 + 3 i) by graphing. Check Add by combining the real parts and combining the imaginary parts. (3 – i) + (2 + 3 i) = (3 + 2) + (–i + 3 i) = 5 + 2 i

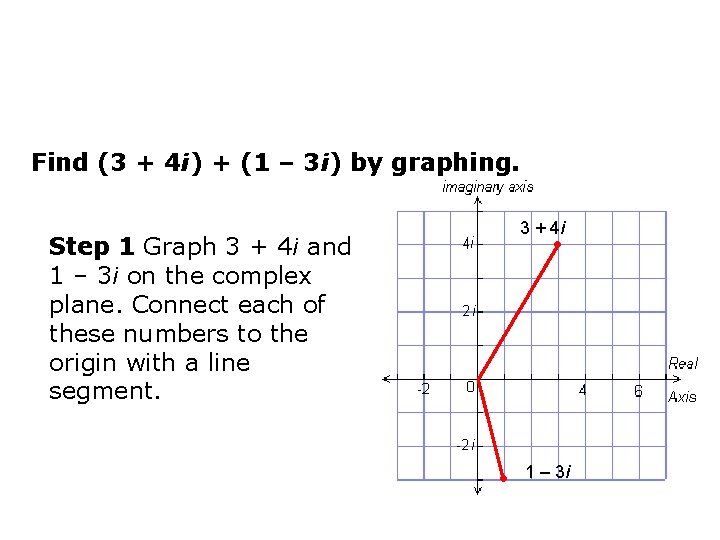
Find (3 + 4 i) + (1 – 3 i) by graphing. 3 + 4 i • Step 1 Graph 3 + 4 i and 1 – 3 i on the complex plane. Connect each of these numbers to the origin with a line segment. • 1 – 3 i

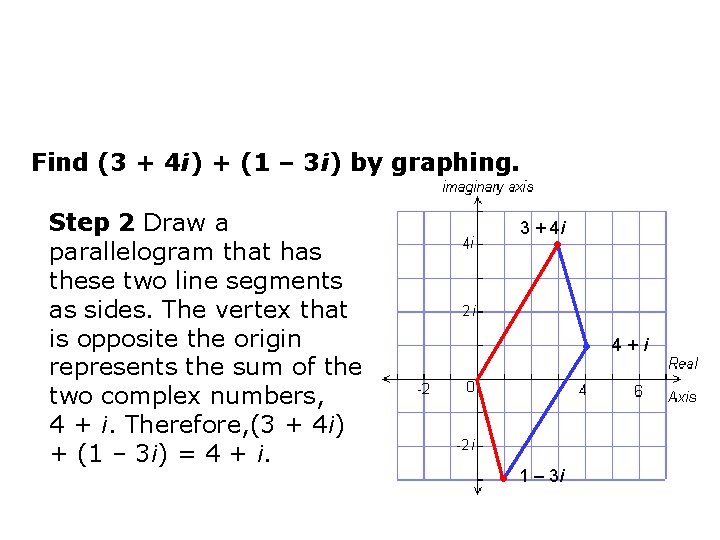
Find (3 + 4 i) + (1 – 3 i) by graphing. Step 2 Draw a parallelogram that has these two line segments as sides. The vertex that is opposite the origin represents the sum of the two complex numbers, 4 + i. Therefore, (3 + 4 i) + (1 – 3 i) = 4 + i. 3 + 4 i • • • 1 – 3 i 4+i
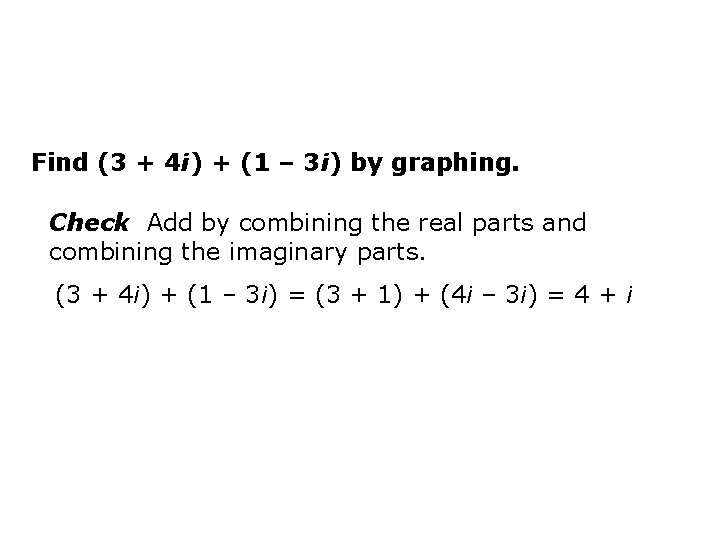
Find (3 + 4 i) + (1 – 3 i) by graphing. Check Add by combining the real parts and combining the imaginary parts. (3 + 4 i) + (1 – 3 i) = (3 + 1) + (4 i – 3 i) = 4 + i

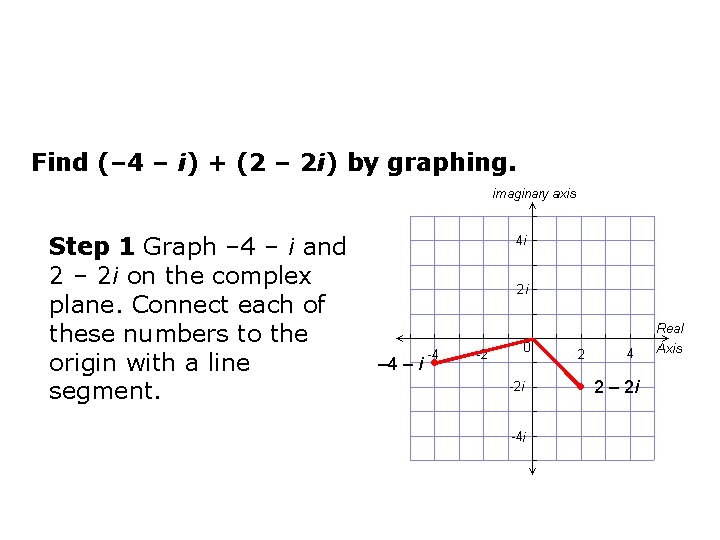
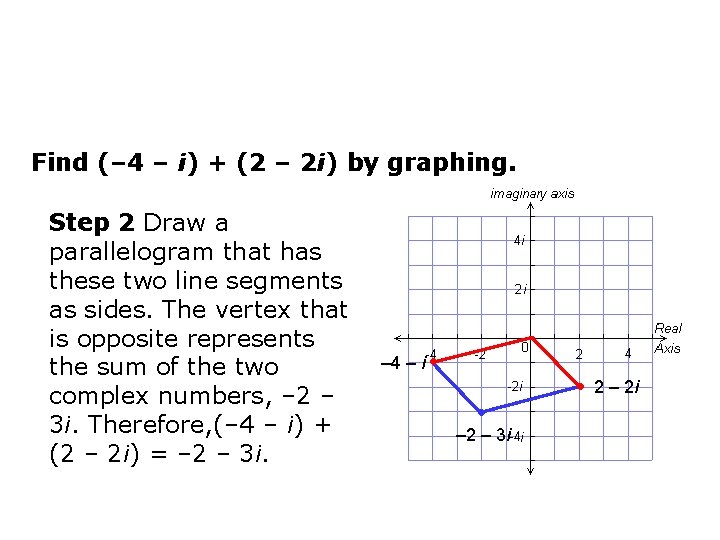
Find (– 4 – i) + (2 – 2 i) by graphing. Step 1 Graph – 4 – i and 2 – 2 i on the complex plane. Connect each of these numbers to the origin with a line segment. – 4 – i • 2 – 2 i • ● 2 – 2 i

Find (– 4 – i) + (2 – 2 i) by graphing. Step 2 Draw a parallelogram that has these two line segments as sides. The vertex that is opposite represents the sum of the two complex numbers, – 2 – 3 i. Therefore, (– 4 – i) + (2 – 2 i) = – 2 – 3 i. – 4 – i • • – 2 – 3 i • 2 – 2 i

Find (– 4 – i) + (2 – 2 i) by graphing. Check Add by combining the real parts and combining the imaginary parts. (– 4 – i) + (2 – 2 i) = (– 4 + 2) + (–i – 2 i) = – 2 – 3 i

Warm UP

Rationalizing the Denominator • Recall that expressions in simplest form cannot have square roots in the denominator. • Because the imaginary unit represents a square root, you must rationalize any denominator that contains an imaginary unit. • To do this, multiply the numerator and denominator by the complex conjugate of the denominator. Helpful Hint The complex conjugate of a complex number a + bi is a – bi. (Lesson 5 -5)

Dividing Complex Numbers Simplify. Multiply by the conjugate. Distribute. Use i 2 = – 1. Simplify.

Dividing Complex Numbers Simplify. Multiply by the conjugate. Distribute. Use i 2 = – 1. Simplify.

Simplify. Multiply by the conjugate. Distribute. Use i 2 = – 1. Simplify.

Simplify. Multiply by the conjugate. Distribute. Use i 2 = – 1. Simplify.

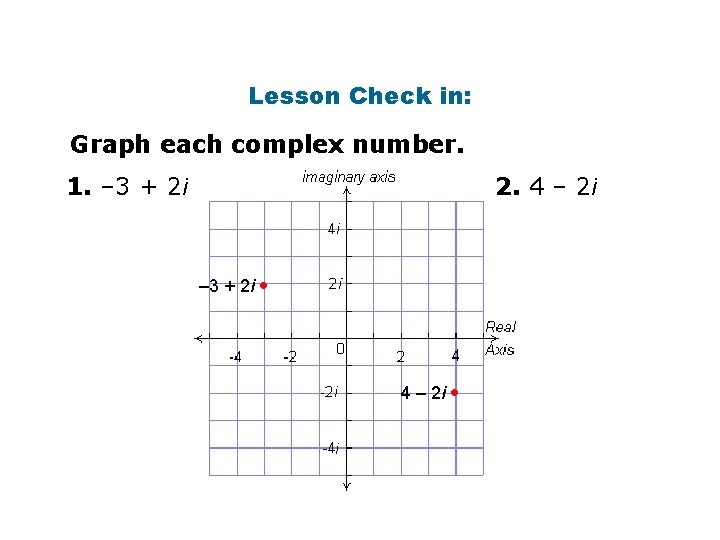
Lesson Check in: Graph each complex number. 1. – 3 + 2 i 2. 4 – 2 i – 3 + 2 i • 4 – 2 i •

3. Find |7 + 3 i|. Perform the indicated operation. Write the result in the form a + bi. 4. (2 + 4 i) + (– 6 – 4 i) – 4 5. (5 – i) – (8 – 2 i) – 3 + i 6. (2 + 5 i)(3 – 2 i) 16 + 11 i 7. 8. Simplify i 31. –i 3+i
 Math lesson
Math lesson Random sampling over joins revisited
Random sampling over joins revisited Quadratics unit test
Quadratics unit test Lic table no 817
Lic table no 817 1-817-868-2300
1-817-868-2300 Ct dot form 817
Ct dot form 817 Sprat qrp
Sprat qrp Day 1 day 2 day 817
Day 1 day 2 day 817 Unit 10, unit 10 review tests, unit 10 general test
Unit 10, unit 10 review tests, unit 10 general test Unit test algebra 2
Unit test algebra 2 The power of mathematical visualization season 1
The power of mathematical visualization season 1 Solving quadratics by square roots
Solving quadratics by square roots Solving quadratics
Solving quadratics Factoring method quadratic equations
Factoring method quadratic equations Quadratics review
Quadratics review Equal roots higher maths
Equal roots higher maths Quadratic equations factored form
Quadratic equations factored form Mr bartons maths
Mr bartons maths Quadratics jeopardy
Quadratics jeopardy Solving quadratics jeopardy
Solving quadratics jeopardy Factorising quadratics
Factorising quadratics Drfrostmaths
Drfrostmaths Quadratic functions examples word problems
Quadratic functions examples word problems The standard form of a quadratic equation is
The standard form of a quadratic equation is X^2-27 factor
X^2-27 factor Nature of roots nat 5
Nature of roots nat 5 Diamond factor method
Diamond factor method Rearranging formulae dr frost
Rearranging formulae dr frost How to factor special cases
How to factor special cases Factoring jeopardy
Factoring jeopardy What is the vertex form of a quadratic equation
What is the vertex form of a quadratic equation Facts about quadratics
Facts about quadratics Criss cross factoring
Criss cross factoring Maxmin
Maxmin Hidden quadratics
Hidden quadratics Investigating quadratics
Investigating quadratics Mystery pictures to solve
Mystery pictures to solve Quadratic formula calculator
Quadratic formula calculator Solve the following equation by completing the square
Solve the following equation by completing the square Dr frost quadratic graphs
Dr frost quadratic graphs Quadratic formula gcse
Quadratic formula gcse Factorising quadratics
Factorising quadratics Quadratic formula review
Quadratic formula review Types of roots in maths
Types of roots in maths Lesson 15 using the quadratic formula
Lesson 15 using the quadratic formula Algebra 2 quadratics review
Algebra 2 quadratics review Factoring ax^2 + bx + c
Factoring ax^2 + bx + c Inequalities dr frost
Inequalities dr frost Factorising quadratics cross method
Factorising quadratics cross method Right triangle trigonometry
Right triangle trigonometry Suatu lembaga yang
Suatu lembaga yang English system conversion
English system conversion Unit cost rekam medis
Unit cost rekam medis Unit process and unit operation
Unit process and unit operation Difference between unit process and unit operation
Difference between unit process and unit operation Setiap unit akuntansi dianggap sebagai unit yang mandiri
Setiap unit akuntansi dianggap sebagai unit yang mandiri Fe³⁺ and o²⁻
Fe³⁺ and o²⁻ Unit 9 test right triangles and trigonometry
Unit 9 test right triangles and trigonometry Unit 6 test radical functions
Unit 6 test radical functions Unit 5 comprehension test asl
Unit 5 comprehension test asl Unit 4 lesson 4 factoring to solve quadratic equations
Unit 4 lesson 4 factoring to solve quadratic equations Unit 1 study guide answer key
Unit 1 study guide answer key The victorian age 1832 to 1901 unit test
The victorian age 1832 to 1901 unit test Khubris
Khubris Mockolás
Mockolás South asia unit test
South asia unit test The number of test of adequacy is
The number of test of adequacy is A student examines the winged insect shown below
A student examines the winged insect shown below Prince escalus was related to two of the slain people
Prince escalus was related to two of the slain people Pl sql unit testing
Pl sql unit testing Stretching and shrinking investigation 3 answers
Stretching and shrinking investigation 3 answers Asl cities
Asl cities Legislative branch unit test
Legislative branch unit test Unit 31 review questions
Unit 31 review questions Hamlet final test
Hamlet final test Unit 3 quadrilaterals and coordinate proof
Unit 3 quadrilaterals and coordinate proof Reasoning and proof unit test
Reasoning and proof unit test Temperate region
Temperate region Function operations multiplication
Function operations multiplication Energy and forces unit test
Energy and forces unit test Solving inequalities unit test part 1
Solving inequalities unit test part 1 Expressions equations and inequalities unit test
Expressions equations and inequalities unit test Unit 2 study guide answer key
Unit 2 study guide answer key Romanticism vs gothic
Romanticism vs gothic Managing credit unit assessment
Managing credit unit assessment Ap psychology unit 8 motivation and emotion test
Ap psychology unit 8 motivation and emotion test Chemistry unit 3 test answer key
Chemistry unit 3 test answer key Canterbury tales test review
Canterbury tales test review Master asl unit 4 pdf
Master asl unit 4 pdf Ap psychology chapter 11
Ap psychology chapter 11 Unit test aaa
Unit test aaa Tat test ap psychology
Tat test ap psychology Correlational research psychology
Correlational research psychology Unit 6 competency test answers
Unit 6 competency test answers Focus 2 test unit 4
Focus 2 test unit 4 Unit 2 american romanticism
Unit 2 american romanticism Dr griggs the crucible
Dr griggs the crucible Africa geography unit test study guide
Africa geography unit test study guide Chain syllogism
Chain syllogism Stat root word
Stat root word Unit 1 test a spanish 2
Unit 1 test a spanish 2 6. evaluate
6. evaluate Middle ages unit test answers
Middle ages unit test answers Geometry test
Geometry test