TURNIRI uvod Vojislav Petrovi Departman za matematiku i

TURNIRI uvod Vojislav Petrović Departman za matematiku i informatiku Novi Sad vojpet@dmi. uns. ac. rs vojpet@gmail. com

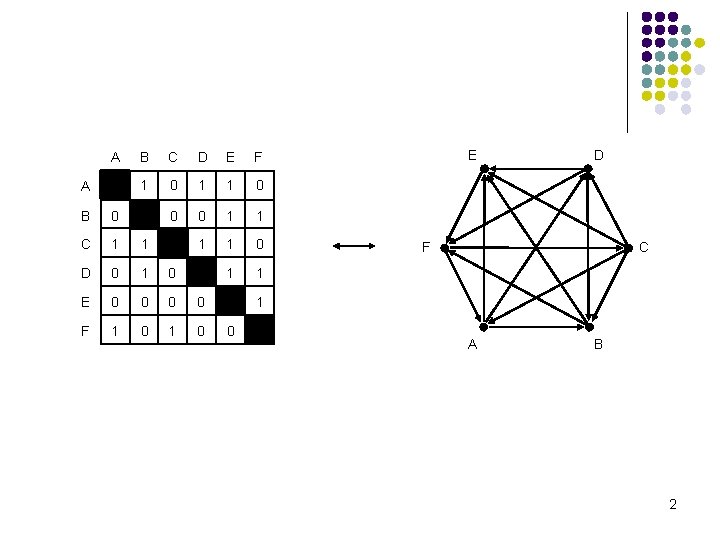
A A B C D E F 1 0 1 1 0 0 0 1 1 B 0 C 1 1 D 0 1 0 E 0 0 F 1 0 E D F C 1 0 A B 2

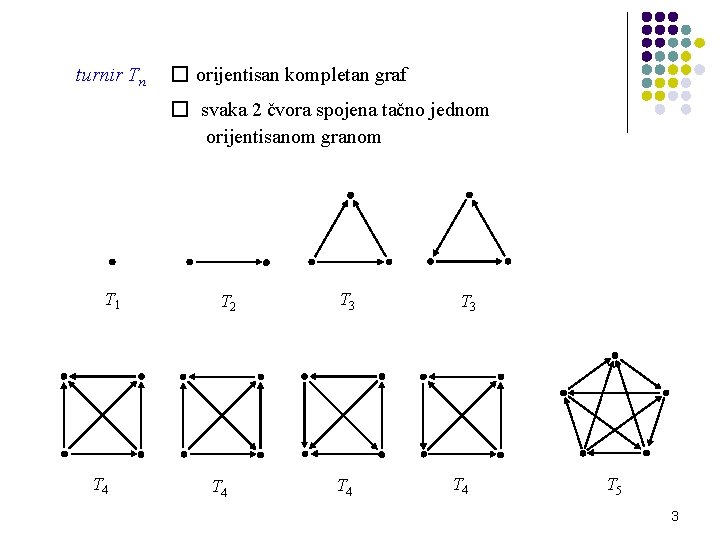
turnir Tn � orijentisan kompletan graf � svaka 2 čvora spojena tačno jednom orijentisanom granom T 1 T 4 T 2 T 4 T 3 T 4 T 5 3

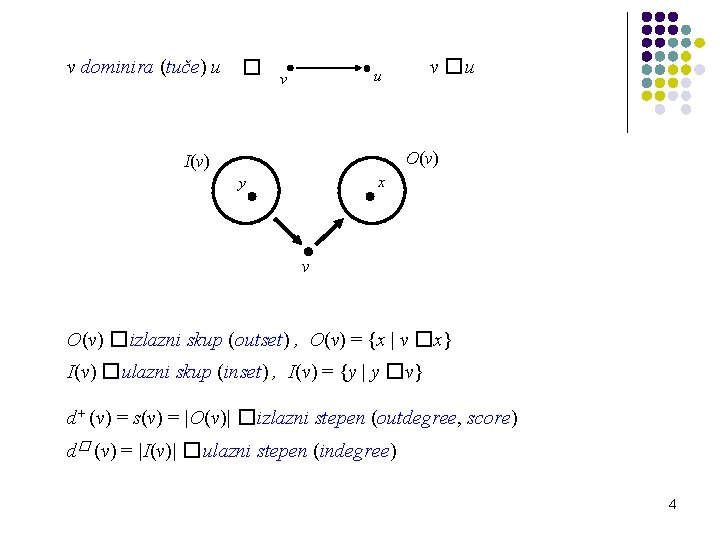
v dominira (tuče) u � v �u u v O(v) I(v) x y v O(v) �izlazni skup (outset) , O(v) = {x | v �x} I(v) �ulazni skup (inset) , I(v) = {y | y �v} d+ (v) = s(v) = |O(v)| �izlazni stepen (outdegree, score) d� (v) = |I(v)| �ulazni stepen (indegree) 4

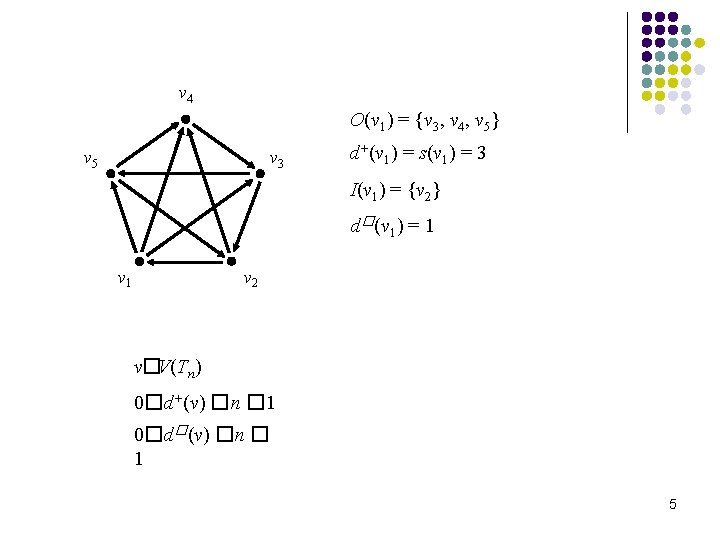
v 4 O(v 1) = {v 3, v 4, v 5} v 5 v 3 d+(v 1) = s(v 1) = 3 I(v 1) = {v 2} d�(v 1) = 1 v 2 v�V(Tn) 0�d+(v) �n � 1 0�d�(v) �n � 1 5

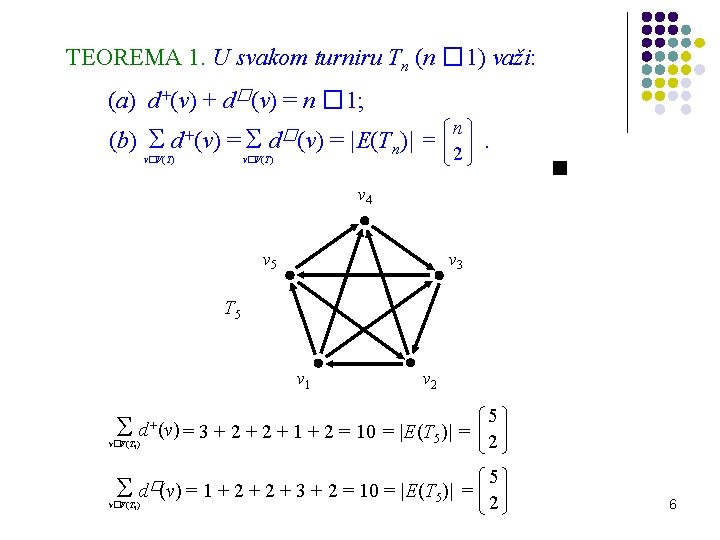
TEOREMA 1. U svakom turniru Tn (n � 1) važi: (a) d+(v) + d�(v) = n � 1; (b) Σ d+(v) = Σ d�(v) = |E(Tn)| = v�V(T) n 2 . v 4 v 5 v 3 T 5 v 1 v 2 Σ d+(v) = 3 + 2 + 1 + 2 = 10 = |E(T 5)| = v�V(T 5) Σ d�(v) v�V(T 5) 5 2 5 = 1 + 2 + 3 + 2 = 10 = |E(T 5)| = 2 6

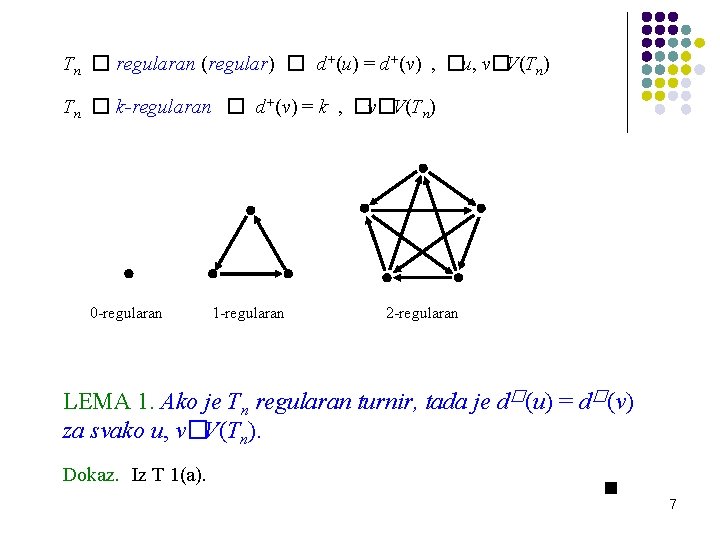
Tn � regularan (regular) � d+(u) = d+(v) , �u, v�V(Tn) Tn � k-regularan � d+(v) = k , �v�V(Tn) 0 -regularan 1 -regularan 2 -regularan LEMA 1. Ako je Tn regularan turnir, tada je d�(u) = d�(v) za svako u, v�V(Tn). Dokaz. Iz T 1(a). 7

LEMA 2. Ako je Tn regularan turnir, tada je n neparan broj. Dokaz. d+(v) = k � 0 T 1(b) � � d+(v) v�V(Tn) = nk = n 2 = n(n � 1) 2 � k= n � 1 2 k�N �{0} � n � 1 (mod 2) PITANJE 1. Da li za svaki neparan prirodan broj n postoji regularan turnir Tn ? Odgovor � DA 8

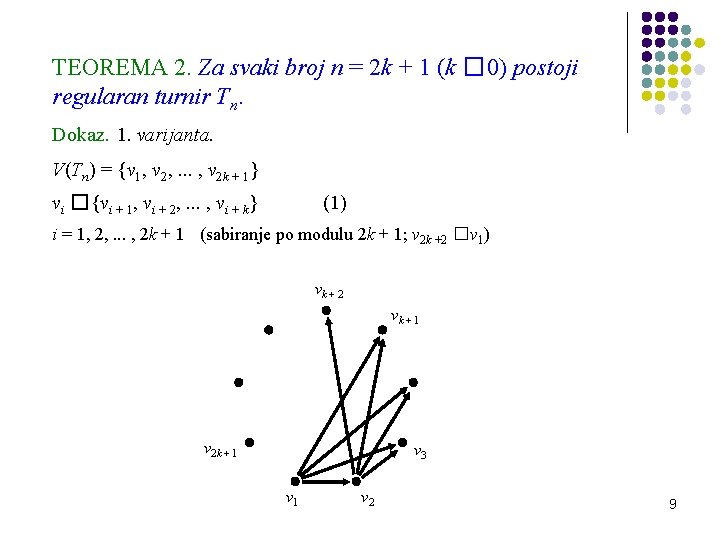
TEOREMA 2. Za svaki broj n = 2 k + 1 (k � 0) postoji regularan turnir Tn. Dokaz. 1. varijanta. V(Tn) = {v 1, v 2, . . . , v 2 k + 1} vi �{vi + 1, vi + 2, . . . , vi + k} (1) i = 1, 2, . . . , 2 k + 1 (sabiranje po modulu 2 k + 1; v 2 k +2 �v 1) vk + 2 vk + 1 v 2 k + 1 v 3 v 1 v 2 9

E(Tn) � dobro definisano {vi, vj} �{v 1, v 2, . . . , v 2 k + 1} � vi �vj �vi j �i + s (mod 2 k + 1) (2) 1 o 1 �s �k (2), 1 o � i �j �s �j + 2 k + 1 � �j + t (mod 2 k + 1) , k �t � s 2 k o (1), (2), 1 � vi �vj (1), (3) � vj �vi (3) 2 o k + 1 �s � 2 k (2), 2 o � i �j + t (mod 2 k + 1) , 1 �t �k (1), (4) � vj �vi (4) (1), (2), 2 o � vi �vj 10

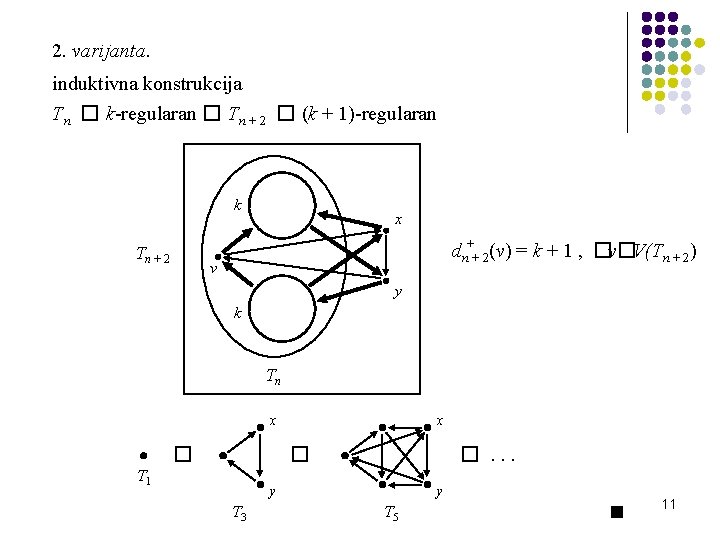
2. varijanta. induktivna konstrukcija Tn � k-regularan � Tn + 2 � (k + 1)-regularan k Tn + 2 x dn++ 2(v) = k + 1 , �v�V(Tn + 2) v y k Tn x �. . . � T 1 y T 3 y T 5 11

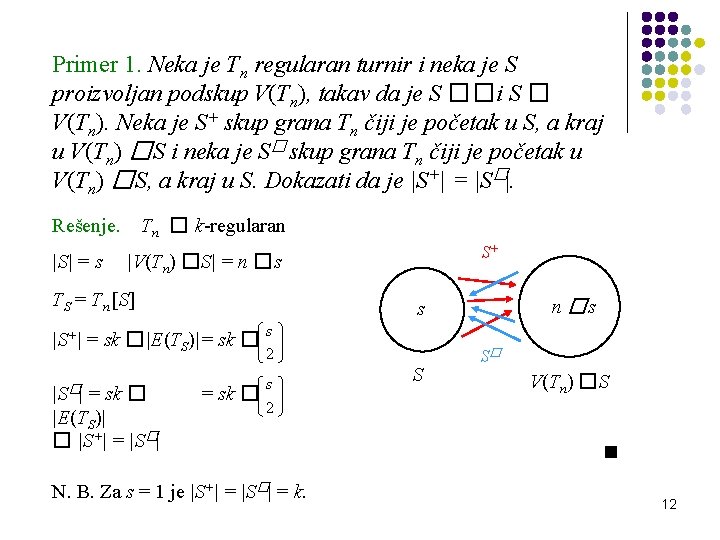
Primer 1. Neka je Tn regularan turnir i neka je S proizvoljan podskup V(Tn), takav da je S ��i S � V(Tn). Neka je S+ skup grana Tn čiji je početak u S, a kraj u V(Tn) �S i neka je S� skup grana Tn čiji je početak u V(Tn) �S, a kraj u S. Dokazati da je |S+| = |S�|. Rešenje. |S| = s Tn � k-regularan S+ |V(Tn) �S| = n �s TS = Tn [S] |S+| = sk �|E(TS)| = sk � s 2 |S�| s 2 = sk � |E(TS)| � |S+| = |S�| n �s s = sk � N. B. Za s = 1 je |S+| = |S�| = k. S S� V(Tn) �S 12

(x 1�xk) �put x 1 x 2 xk� 1 xk xi � xj i � j Pk = x 1 � x 2 �. . . � xk � 1 � xk d (Pk) � dužina puta Pk = broj grana Pk = |E(Pk)| = k � 1 d (u, v) � rastojanje od u do v = dužina najkraćeg (u�v) � def. puta d (u, u) = 0 def. ne postoji (u�v) � � d (u, v) = � put d(Tn) �dijametar turnira Tn d(Tn) = max d(u, v) u, v�V(Tn) N. B. U turniru je uvek d (v, u) �d (u, v)! 13

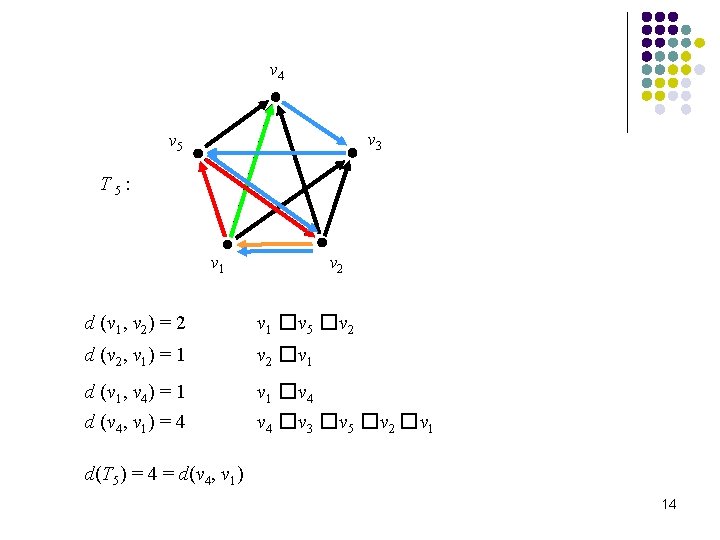
v 4 v 3 v 5 T 5: v 1 v 2 d (v 1, v 2) = 2 v 1 � v 5 � v 2 d (v 2, v 1) = 1 v 2 � v 1 d (v 1, v 4) = 1 d (v 4, v 1) = 4 v 1 � v 4 � v 3 � v 5 � v 2 � v 1 d(T 5) = 4 = d(v 4, v 1) 14

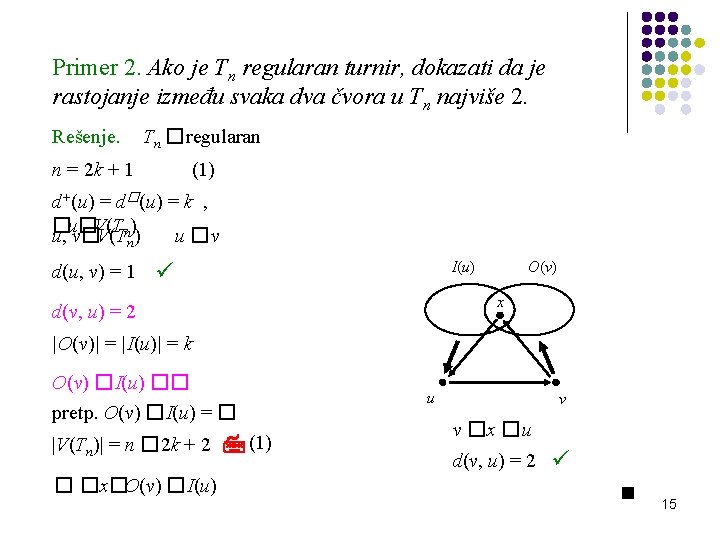
Primer 2. Ako je Tn regularan turnir, dokazati da je rastojanje između svaka dva čvora u Tn najviše 2. Rešenje. Tn �regularan n = 2 k + 1 (1) d+(u) = d�(u) = k , � u, u� v�V(T V(Tn)) u �v n d(u, v) = 1 I(u) O(v) x d(v, u) = 2 |O(v)| = |I(u)| = k O(v) �I(u) �� pretp. O(v) �I(u) = � |V(Tn)| = n � 2 k + 2 � �x�O(v) �I(u) (1) u v v �x �u d(v, u) = 2 15

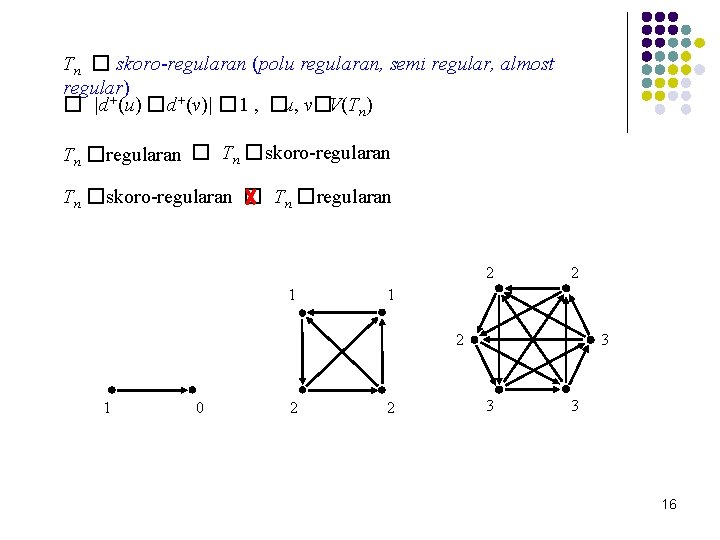
Tn � skoro-regularan (polu regularan, semi regular, almost regular) � |d+(u) �d+(v)| � 1 , �u, v�V(Tn) Tn �regularan � Tn �skoro-regularan � Tn �regularan 2 1 2 1 0 2 2 3 3 3 16

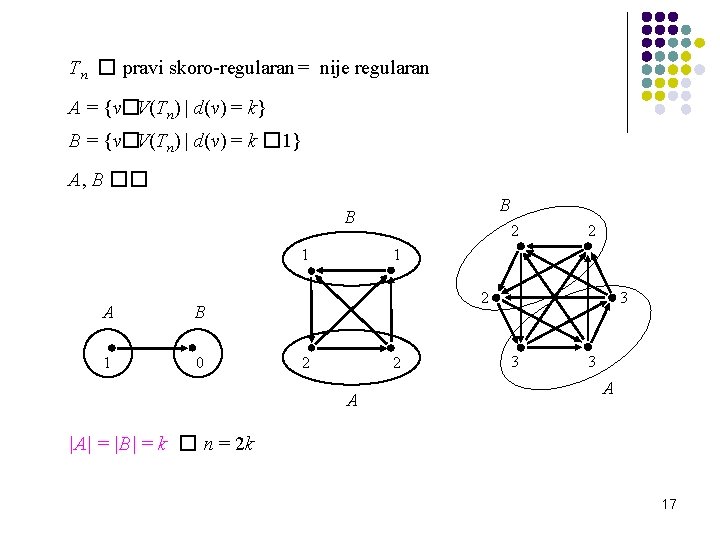
Tn � pravi skoro-regularan = nije regularan A = {v�V(Tn) | d(v) = k} B = {v�V(Tn) | d(v) = k � 1} A, B �� B B 1 A B 1 0 2 2 1 2 2 2 A 3 3 3 A |A| = |B| = k � n = 2 k 17

LEMA 3. Ako je Tn pravi skoro-regularan turnir, tada je n n paran broj i |A| = |B| = 2. Dokaz. Tn � pravi skoro-regularan turnir A = {v�V(Tn) | d(v) = k} |A| = a B = {v�V(Tn) | d(v) = k � 1} (1) � a + b = n , a > 0 , b > 0 ak + b(k � 1) �k= n+1 2 � k< n+1 2 (2) |B| = b (2) = ak + (n �a) (k � = |E(Tn)| = 1) a �n (1) n 2 = n(n � 1) 2 (3) (4) 18

PITANJE 2. Da li za svaki paran prirodan broj n postoji pravi skoro-regularan turnir Tn ? Odgovor � DA TEOREMA 3. Za svaki broj n = 2 k (k � 1) postoji pravi skoro-regularan turnir Tn. Dokaz. Kao za T 2. V(Tn) = �v 1, . . . , vk + 1, . . . , v 2 k� A = �v 1, . . . , B = �vk + 1, . . . , v 2 k� vk � 1. varijanta. vi �{vi + 1, . . . , vi + k} i = 1, . . . , k vi �{vi + 1, . . . , vi + k � 1} i = k + 1, . . . , 2 k (sabiranje po modulu 2 k ; v 2 k +1 �v 1) vk + 2 vk + 1 vk (1) v 2 k v 3 v 1 v 2 20

E(Tn) � dobro definisano {vi, vj} �{v 1, v 2, . . . , v 2 k} � vi �vj �vi A = �v 1, . . . , B = �vk + 1, . . . , v 2 k� vk � (a) vi, vj�A � vi, vj�B , i � (1) j j = i + t , 1 � t � k � � vi � vj 1 i = j �t �j + 2 k � �j + s (mod 2 k) k + 1 �s � 2 k � t 1 (1) � vj �vi (b) vi�A � vj�B � i �j (1) vj �vi kao u (a) j � i � � vi � vj k v 1 �vk + 1 v 3 �vk + 2 vk �v 2 k (1) vi �vj kao u (a) j � i � k � vj � vi vk + 2 �v 1 vk + 4 �v 3 v 2 k �v 2 (k � 3) 21

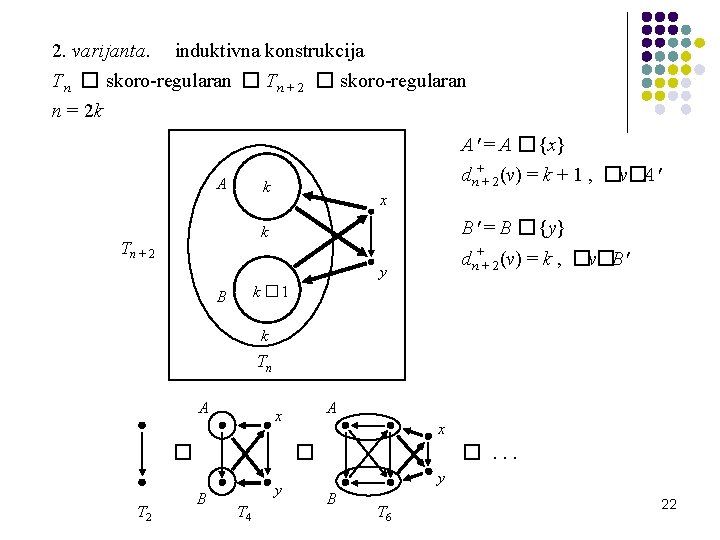
2. varijanta. induktivna konstrukcija Tn � skoro-regularan � Tn + 2 � skoro-regularan n = 2 k A' = A �{x} A dn++ 2(v) = k + 1 , �v�A' k x B' = B �{y} k Tn + 2 dn++ 2(v) = k , �v�B' y k � 1 B k Tn A � T 2 A x x �. . . � B y T 4 y B T 6 22

ZADATAK 1. Ako je Tn pravi skoro regularan turnir i S �V(Tn), šta se može reći o razlici |S+| �|S�|? (Videti primer 1. ) 23

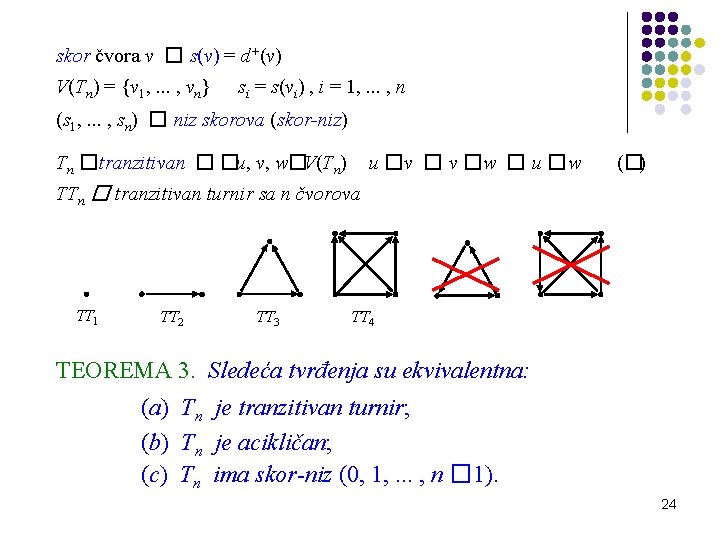
skor čvora v � s(v) = d+(v) V(Tn) = {v 1, . . . , vn} si = s(vi) , i = 1, . . . , n (s 1, . . . , sn) � niz skorova (skor-niz) Tn �tranzitivan � �u, v, w�V(Tn) u �v � v �w � u �w (�) TTn � tranzitivan turnir sa n čvorova TT 1 TT 2 TT 3 TT 4 TEOREMA 3. Sledeća tvrđenja su ekvivalentna: (a) Tn je tranzitivan turnir; (b) Tn je acikličan; (c) Tn ima skor-niz (0, 1, . . . , n � 1). 24

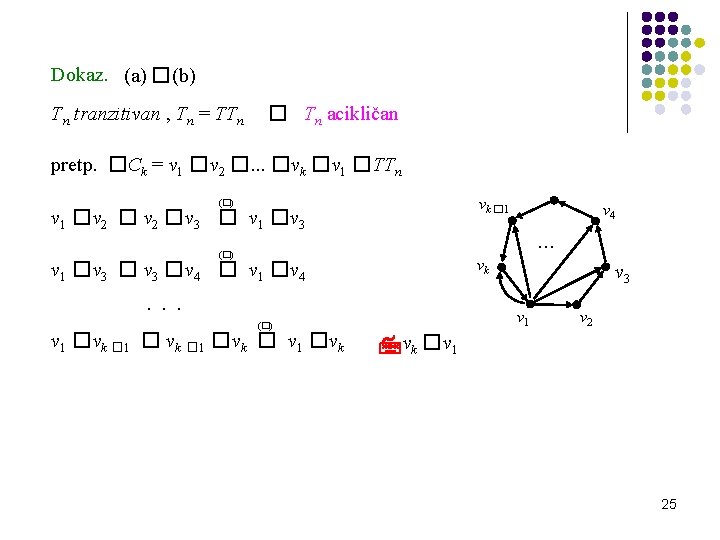
Dokaz. (a) �(b) Tn tranzitivan , Tn = TTn � Tn acikličan pretp. �Ck = v 1 �v 2 �. . . �vk �v 1 �TTn vk � 1 (�) v 1 � v 2 � v 3 � v 1 � v 3 . . . (�) vk v 1 � v 3 � v 4 � v 1 � v 4. . . v 3 v 1 (�) v 1 � vk � v 1 � vk v 4 v 2 vk �v 1 25

Primer 3. Na jednom turniru učestvovalo je n (n � 3) ekipa i pritom je svaka odigrala sa svakom po jedan meč koji se završio pobedom jedne od ekipa. Za neke tri ekipe A, B, C, A je pobedila B, B je pobedila C i C je pobedila A. Dokazati da su na kraju turnira bile bar dve ekipe koje su imale isti broj pobeda. Rešenje. Tn A �B �C �A V(Tn) = �A, B, C, . . . � T 3(b) � Tn nije tranzitivan , Tn �TTn T 3(c) � skor-niz Tn �(0, 1, . . . , n � 1) � �X, Y�V(Tn) , s(X) = s(Y) 28

Hamiltonov put u Tn � (orijentisan) put koji sadrži sve čvorove Tn TEOREMA 4. (Rédei 1934) Svaki turnir Tn sadrži Hamiltonov put. Dokaz. indukcijom po n n=1 n=2 T 1 T 2 ind. hipoteza Svaki turnir Tm (m < n, n > 2) sadrži Hamiltonov put. Tn , n > 2 V(Tn) = {v 1, . . . , vn} Tn � 1 = Tn � v n ind. hip. � Tn � 1 sadrži Hamiltonov put Pn � 1 = v 1 �v 2 �. . . �vn � 1 v 2 vn � 1 29

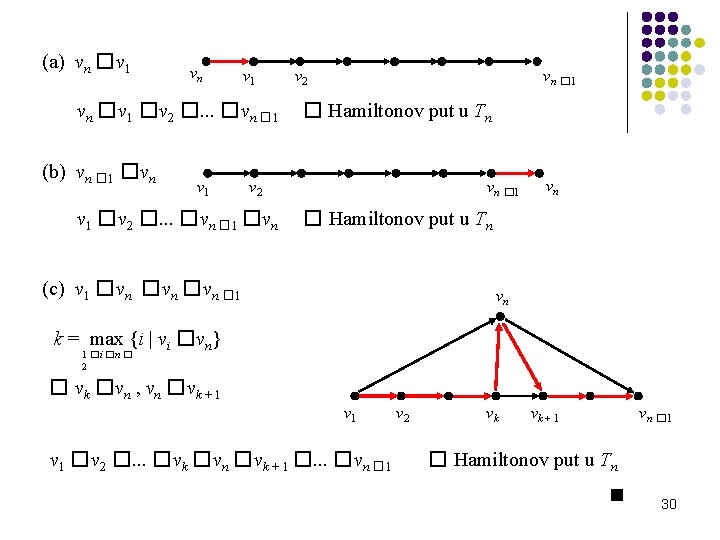
(a) vn �v 1 �v 2 �. . . �vn � 1 (b) vn � 1 �vn v 1 v 2 vn � 1 � Hamiltonov put u Tn v 2 v 1 �v 2 �. . . �vn � 1 �vn vn � 1 vn � Hamiltonov put u Tn (c) v 1 �vn �vn � 1 vn k = max {i | vi �vn} 1 �i �n � 2 � vk � vn , vn � vk + 1 v 1 �v 2 �. . . �vk �vn �vk + 1 �. . . �vn � 1 v 2 vk vn � 1 vk + 1 � Hamiltonov put u Tn 30

ZADATAK 2. Neka je s 1, s 2, . . . , sn niz skorova (izlaznih stepena) turnira Tn. Šta se može reći o tom turniru ako jednakost k k Σ si = 2 i=1 važi za svako k, 1 �k �n? ZADATAK 3. Dokazati da u svakom turniru sa 8 čvorova postoje 4 čvora x, y, z, t, takva da je x �{y, z, t}, y �{z, t}, z � t. ZADATAK 4. Dokazati da svaki turnir sa 2 k � 1 (k � 1) čvorova sadrži tranzitivan podturnir sa k čvorova. . ZADATAK 5. Dokazati da je turnir tranzitivan ako i samo ako ima jedinstven Hamiltonov put. 31

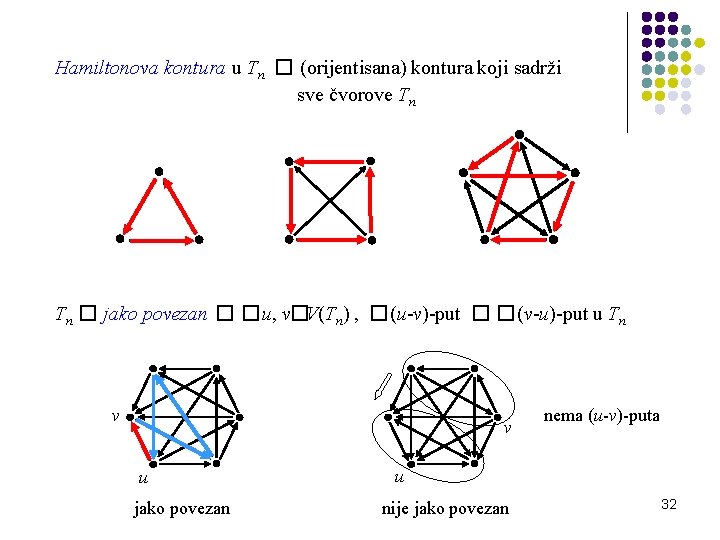
Hamiltonova kontura u Tn � (orijentisana) kontura koji sadrži sve čvorove Tn Tn � jako povezan � �u, v�V(Tn) , �(u-v)-put � �(v-u)-put u Tn v v u jako povezan nema (u-v)-puta u nije jako povezan 32

TEOREMA 5. (Camion 1959) Turnir Tn (n � 3) sadrži Hamiltonovu konturu ako i samo ako je jako povezan. Dokaz. V(Tn) = {v 1, . . . , vn} (�) Tn sadrži Hamiltonovu konturu Tn �jako povezan vj vi + 1 Cn = v 1 �v 2 �. . . �vn �v 1 vj + 1 vi , vj�V(Tn) vi �vi + 1 �. . . �vj � (vi - vj)-put vj �vj + 1 �. . . �vi � (vj - vi)-put vi Cn vn v 1 v 2 (indeksi po mod n ; vn + 1 = v 1. . . ) � Tn jako povezan 33

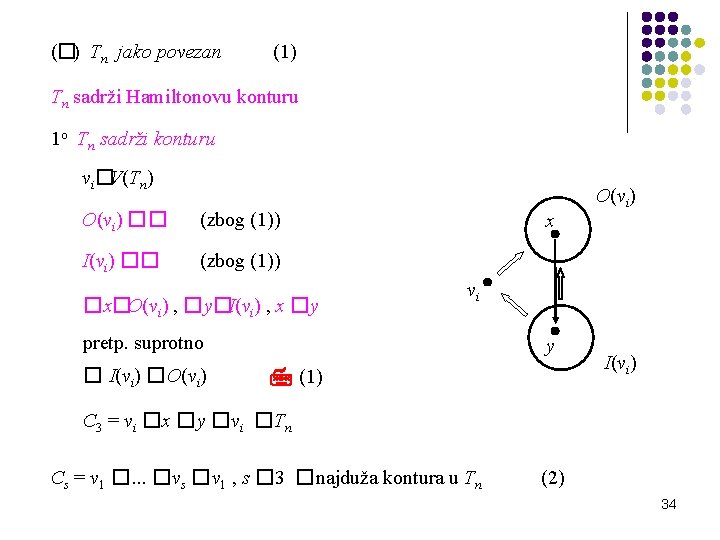
(�) Tn jako povezan (1) Tn sadrži Hamiltonovu konturu 1 o Tn sadrži konturu vi�V(Tn) O(vi) �� (zbog (1)) I(vi) �� (zbog (1)) �x�O(vi) , �y�I(vi) , x �y x vi pretp. suprotno � I(vi) �O(vi) y (1) I(vi) C 3 = v i � x � y � v i � Tn Cs = v 1 �. . . �vs �v 1 , s � 3 �najduža kontura u Tn (2) 34

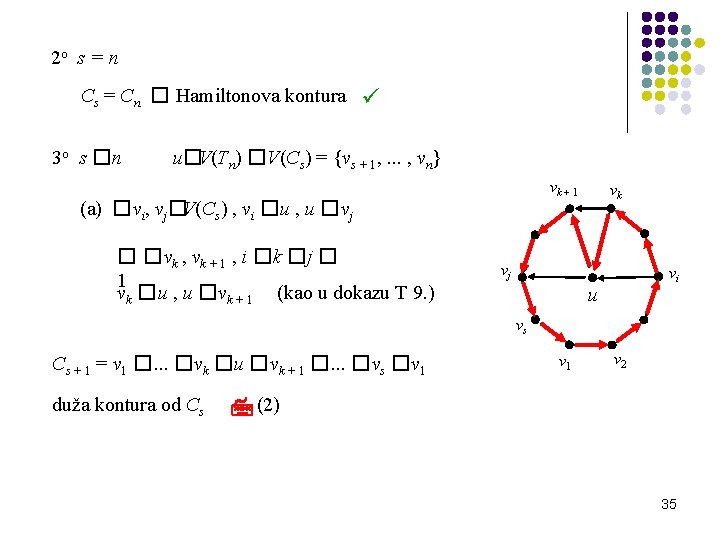
2 o s = n Cs = Cn � Hamiltonova kontura 3 o s �n u�V(Tn) �V(Cs) = {vs + 1, . . . , vn} vk + 1 (a) �vi, vj�V(Cs) , vi �u , u �vj � � vk , vk + 1 , i � k � j � 1 vk �u , u �vk + 1 (kao u dokazu T 9. ) vk vj vi u vs Cs + 1 = v 1 �. . . �vk �u �vk + 1 �. . . �vs �v 1 duža kontura od Cs v 1 v 2 (2) 35

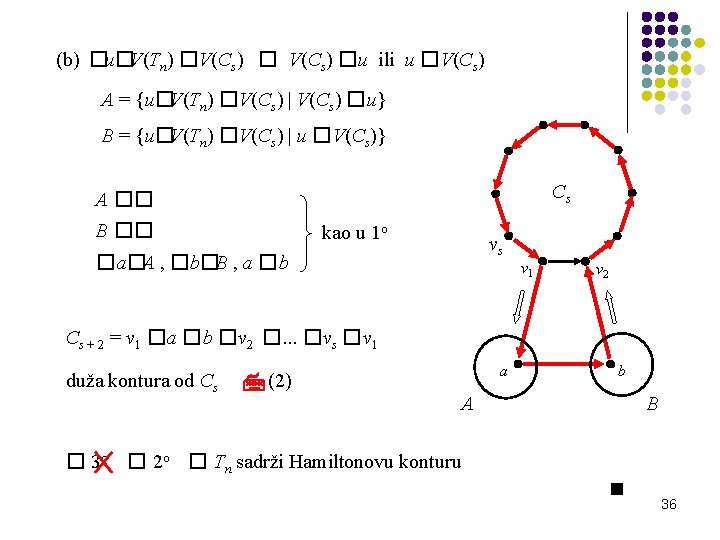
(b) �u�V(Tn) �V(Cs) �u ili u �V(Cs) A = {u�V(Tn) �V(Cs) | V(Cs) �u} B = {u�V(Tn) �V(Cs) | u �V(Cs)} Cs A �� B �� kao u 1 o vs �a�A , �b�B , a �b v 1 v 2 Cs + 2 = v 1 �a �b �v 2 �. . . �vs �v 1 duža kontura od Cs (2) a b B A � 3 o � 2 o � Tn sadrži Hamiltonovu konturu 36

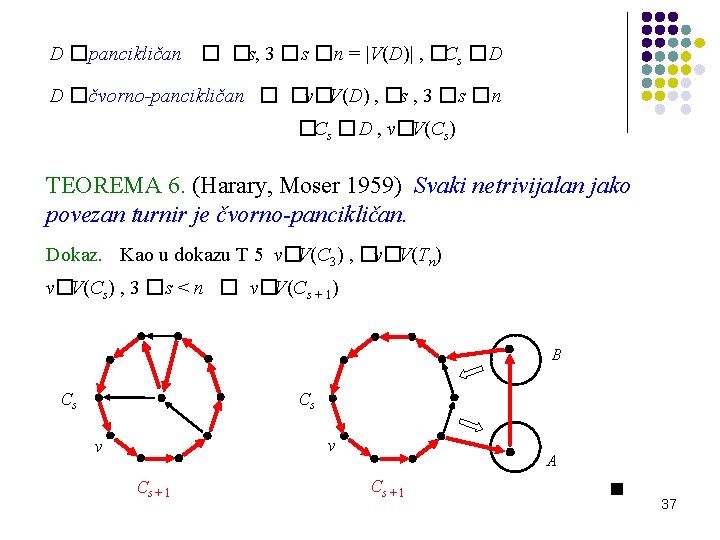
D �pancikličan � �s, 3 �s �n = |V(D)| , �Cs �D D �čvorno-pancikličan � �v�V(D) , �s , 3 �s �n �Cs �D , v�V(Cs) TEOREMA 6. (Harary, Moser 1959) Svaki netrivijalan jako povezan turnir je čvorno-pancikličan. Dokaz. Kao u dokazu T 5 v�V(C 3) , �v�V(Tn) v�V(Cs) , 3 �s < n � v�V(Cs + 1) B Cs Cs v v Cs + 1 A Cs + 1 37

RAZNI ZADACI 1. Dokazati da u svakom turnir Tn postoje čvorovi u i v, takvi da je d+(u) � n � 1 2 i d�(u) � . 2. Na jednom turniru svaki igrač odigrao je sa svakim po jedan meč koji se završio pobedom jednog od njih. Na kraju turnira ispostavilo se da je igrač A imao k, k � 2, pobeda više od igrača B. Dokazati da se može naći grupa igrača S, takva da je �S��k � 1, da je igrač A pobedio sve iz S i da je igrač B izgubio od svih iz S. 3. Ako za čvorove u i v turnira T važi d+(u) �d+(v), tada u T postoji (u-v)-put dužine najviše 2. Dokazati. 4. Dokazati da u svakom turniru T postoji čvor u, takav da je d(u, v) � 2 za svaki čvor v�V(T). (d(u, v) �rastojanje od u do v; d(u, u) = 0. ) 38

5. Za svaka dva čvora x i y turnira T postoji tačno jedan čvor u, takav da u �{x, y} i tačno jedan čvor v, takav da {x, y} �v. Dokazati sledeća tvrđenja: (a) T je regularan; (b)* T ima tačno 7 čvorova. 6. Dokazati da se svaki turnir Tn (n � 3) može transformisati u jako povezan promenom orijentacije najviše jedne grane. 7. Dokazati da svaki jako povezan turnir Tn (n � 4) sadrži čvor v, takav da se promenom orijentacija svih grana incidentnih sa v dobija opet jako povezan turnir. 8. Dokazati da u svakom jako povezanom turniru Tn (n � 4) postoje dva čvora x i y, takvi da su oba turnira Tn �x i Tn �y jako povezana. 39