POVRINE RAVNIH FIGURA Vojislav Petrovi Departman za matematiku

POVRŠINE RAVNIH FIGURA Vojislav Petrović Departman za matematiku i informatiku, PMF Novi Sad vojpet@gmail. com

razloživa jednakost F 1 , F 2 ravne figure P(F 1) , P(F 2) površine F 1 i F 2 F 1 = X 1 X 2 . . . Xn int Xi int Xj = , i j F 2 = Y 1 Y 2 . . . Yn int Yi int Yj = , i j i 1, 2, . . . , n , P(Xi) = P(Yi) P(F 1) = P(F 2) 2

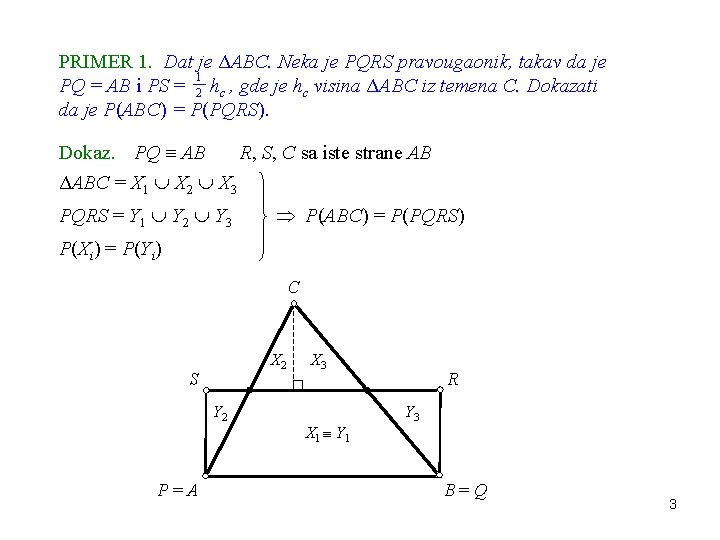
PRIMER 1. Dat je ΔABC. Neka je PQRS pravougaonik, takav da je 1 PQ = AB i PS = 2 hc , gde je hc visina ΔABC iz temena C. Dokazati da je P(ABC) = P(PQRS). Dokaz. PQ AB R, S, C sa iste strane AB ΔABC = X 1 X 2 X 3 PQRS = Y 1 Y 2 Y 3 P(ABC) = P(PQRS) P(Xi) = P(Yi) C X 2 S Y 2 P=A X 3 X 1 Y 1 R Y 3 B=Q 3

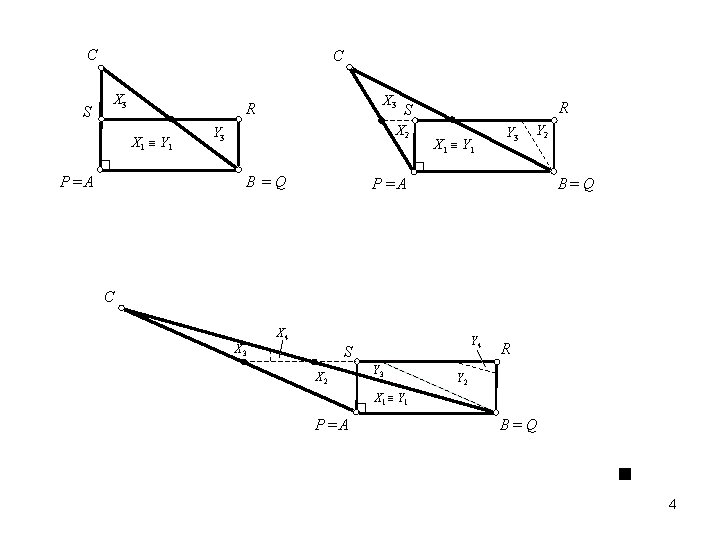
C S C X 3 X 1 Y 1 P =A X 3 R X 2 Y 3 B =Q R S X 1 Y 1 Y 3 Y 2 P =A B= Q C X 4 Y 4 S X 3 X 2 Y 3 R Y 2 X 1 Y 1 P =A B= Q 4

POSLEDICA 1. Površina trougla jednaka je poluproizvodu stranice i odgovarajuće visine. POSLEDICA 2. Trouglovi koji imaju par jednakih stranica i par jednakih, njima odgovarajućih, visina, imaju jednake površine. POSLEDICA 3. Ako je CC 1 težišna linija u ABC, tada je P(AC 1 C) = P(BC 1 C). 5

PRIMER 2. Neka je ABCD trapez sa osnovicama AB i CD i neka je E tačka prave AB, takva da je A B E i BE = CD. Dokazati da je P(ABCD) = P(AEC) = P(AED). Dokaz. ABCD = X 1 X 2 D AEC = Y 1 Y 2 = X 1 Y 2 P(X 2) = P(Y 2) X 2 (Posl. 2) X 1 = Y 1 P(ABCD) = P(X 1) + P(X 2) = P(X 1) + P(Y 2) C Y 2 A B E = P(AEC) Posl. 2 = P(AED) POSLEDICA 4. Površina trapeza jednaka je poluproizvodu zbira osnovica i visine trapeza. 6

dopunska jednakost F 1 , F 2 ravne figure P(F 1) , P(F 2) površine F 1 i F 2 G 1 = F 1 X 1 . . . Xn int F 1 int Xi = , int Xi int Xj = , i j G 2 = F 2 Y 1 . . . Yn int F 2 int Yi = , int Yi int Yj = , i j P(G 1) = P(G 2) i 1, 2, . . . , n , P(Xi) = P(Yi) P(F 1) = P(F 2) 7

PRIMER 3. Neka je ABCD trapez sa osnovicama AB i CD čije se dijagonale seku u tački O. Dokazati da je P(ADO) = P(BCO). Dokaz. F 1 = ADO F 2 = BCO X 1 = Y 1 = ABO G 1 = F 1 X 1 = ABD G 2 = F 2 Y 1 = F 2 X 1 = ABC D C F 1 O F 2 X 1 = Y 1 A B Posl. 2 P(G 1) = P(G 2) P(F 1) = P(F 2) P(ADO) = P(BCO) 8

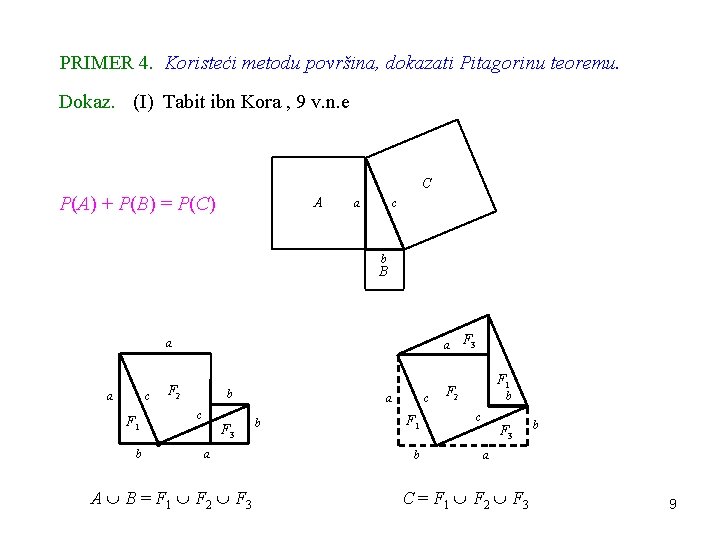
PRIMER 4. Koristeći metodu površina, dokazati Pitagorinu teoremu. Dokaz. (I) Tabit ibn Kora , 9 v. n. e C P(A) + P(B) = P(C) A a c b B a a c F 1 b a F 2 b c F 3 a A B = F 1 F 2 F 3 a b c F 1 b F 3 F 1 F 2 b c F 3 b a C = F 1 F 2 F 3 9

(II) Bhaskara , 7 v. n. e C A P(A) + P(B) = P(C) a c F b B G kvadrat stranice (a + b) a b F b a b F F c a a A C a F c c F F b a G = C 4 F b b F F a B b b G = (A B) 4 F P(C) = P(A) + P(B) N. B. http: //www. cut-the-knot. org/pythagoras/ više od 100 dokaza 10

PRIMER 5. Kroz tačku O, koja leži unutar paralelograma ABCD, povučene su prave s i t, pri čemu je s AB i t AD. Prava s seče stranice AD i BC redom u tačkama S i Q, a prava t stranice AB i CD redom u tačkama P i R. Dokazati da je P(PBQO) = P(RDSO) ako i samo ako O AC. Dokaz. ( ) O AC R D F 1 = PBQO F 2 = RDSO Y 2 F 2 t P(F 1) = P(F 2) X 1 = APO Y 1 = ASO X 2 = CQO Y 2 = CRO G 1 = F 1 X 2 = ABC G 2 = F 2 Y 1 Y 2 = ADC ABCD paralelogram P(G 1) = P(G 2) APOS paralelogram P(X 1) = P(Y 1) OQCR paralelogram P(X 2) = P(Y 2) S s Y 1 O X 1 A P X 2 C Q F 1 B (1) (2) (3) (1), (2), (3) P(F 1) = P(F 2) P(PBQO) = P(RDSO) 11

( ) P(PBQO) = P(RDSO) (4) pretp. O AC O int ABC O int ADC F 1 = PBQO X 1 = APO Y 1 = ASO R D F 2 = RDSO X 2 = CQO Y 2 = CRO Y 2 F 2 X 2 S Y 1 A C O X 1 P Q F 1 B G 1 = F 1 X 2 = ABCO G 2 = F 2 Y 1 Y 2 = ADCO P(G 1) < P(G 2) (5) (6) (4) P(F 1) = P(F 2) APOS paralelogram P(X 1) = P(Y 1) OQCR paralelogram P(X 2) = P(Y 2) (6), (7), (8) P(G 1) = P(G 2) (5) (7) (8) 12

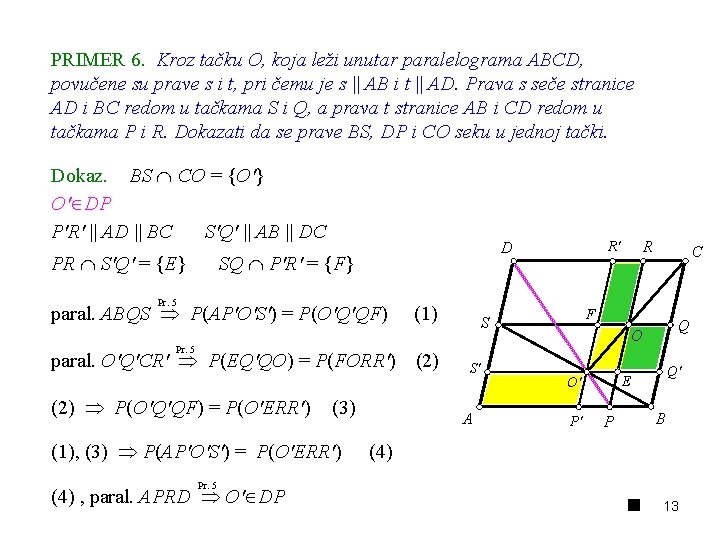
PRIMER 6. Kroz tačku O, koja leži unutar paralelograma ABCD, povučene su prave s i t, pri čemu je s AB i t AD. Prava s seče stranice AD i BC redom u tačkama S i Q, a prava t stranice AB i CD redom u tačkama P i R. Dokazati da se prave BS, DP i CO seku u jednoj tački. Dokaz. BS CO = {O'} O' DP P'R' AD BC S'Q' AB DC PR S'Q' = {E} D SQ P'R' = {F} Pr. 5 paral. ABQS P(AP'O'S') = P(O'Q'QF) Pr. 5 paral. O'Q'CR' P(EQ'QO) = P(FORR') (2) P(O'Q'QF) = P(O'ERR') (3) (1), (3) P(AP'O'S') = P(O'ERR') (1) (2) A C F S S' R R' Q O P' Q' E O' B P (4) Pr. 5 (4) , paral. APRD O' DP 13

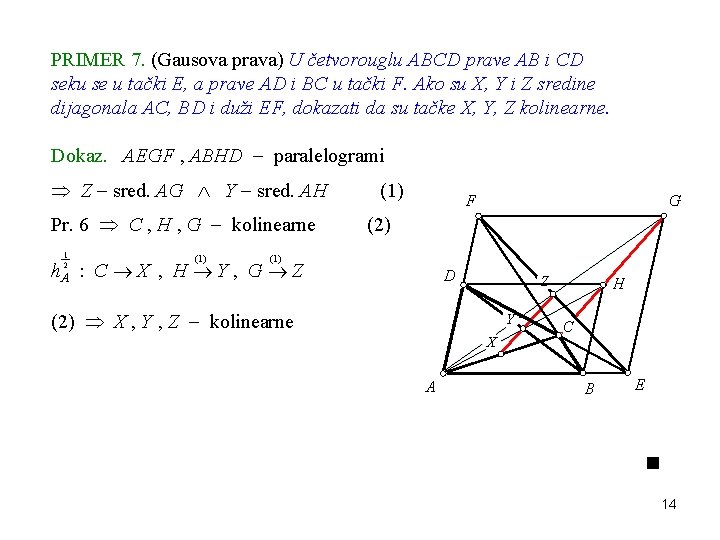
PRIMER 7. (Gausova prava) U četvorouglu ABCD prave AB i CD seku se u tački E, a prave AD i BC u tački F. Ako su X, Y i Z sredine dijagonala AC, BD i duži EF, dokazati da su tačke X, Y, Z kolinearne. Dokaz. AEGF , ABHD paralelogrami Z sred. AG Y sred. AH Pr. 6 C , H , G kolinearne 1 2 (1) F G (2) (1) h. A : C X , H Y , G Z D Z (2) X , Y , Z kolinearne Y X A H C B E 14

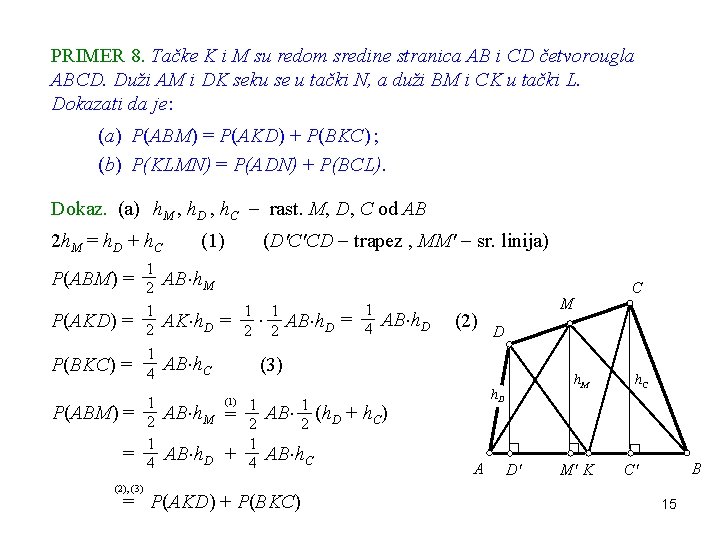
PRIMER 8. Tačke K i M su redom sredine stranica AB i CD četvorougla ABCD. Duži AM i DK seku se u tački N, a duži BM i CK u tački L. Dokazati da je: (a) P(ABM) = P(AKD) + P(BKC) ; (b) P(KLMN) = P(ADN) + P(BCL). Dokaz. (a) h. M , h. D , h. C rast. M, D, C od AB 2 h. M = h. D + h. C AB h. M P(AKD) = 1 2 P(BKC) = 1 4 AB h. C P(ABM) = = 1 2 1 4 (D'C'CD trapez , MM' sr. linija) (1) AK h. D = 1 2 AB h. D = 1 4 AB h. D (2) M D (3) (1) AB h. M = AB h. D + 1 2 1 4 AB 1 2 AB h. C h. M h. D (h. D + h. C) A C D' M' K h. C B C' (2), (3) = P(AKD) + P(BKC) 15

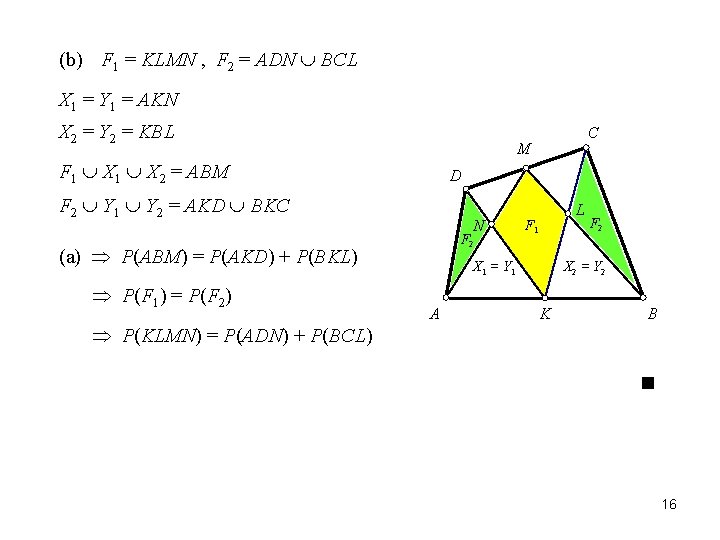
(b) F 1 = KLMN , F 2 = ADN BCL X 1 = Y 1 = AKN X 2 = Y 2 = KBL M F 1 X 2 = ABM D F 2 Y 1 Y 2 = AKD BKC N F 2 (a) P(ABM) = P(AKD) + P(BKL) P(F 1) = P(F 2) P(KLMN) = P(ADN) + P(BCL) C L F 1 X 1 = Y 1 A F 2 X 2 = Y 2 K B 16

PRIMER 9. Tačke K, L, M, N dele svaku od stranica AB i CD konveksnog četvorougla ABCD na po tri jednaka dela kao na slici. Dokazati da je 1 P(KLMN) = 3 P(ABCD). Dokaz. PKLMN = P 2 + Q 2 (1) PABCD = (P 1 + P 2 + P 3) + (Q 1 + Q 2 + Q 3) (2) h. N , h. M , h. C rast. N, M, C od AB 2 h. M = h. N + h. C 2 P 2 = P 1 + P 3 (3) P 1 (4) (2), (3), (4) PABCD = 3 P 2 + 3 Q 2 A Q 3 Q 2 Q 1 . . . slično 2 Q 2 = Q 1 + Q 3 N D K C M P 2 P 3 L B = 3 PKLMN = 1 3 PABCD 17

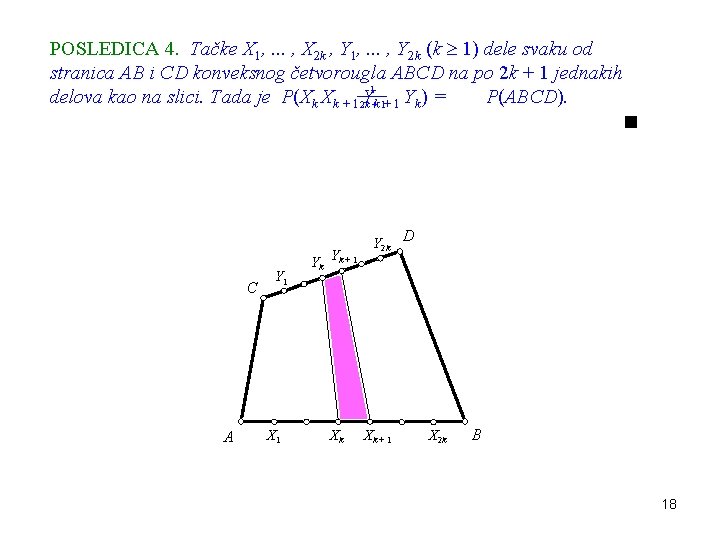
POSLEDICA 4. Tačke X 1, . . . , X 2 k , Y 1, . . . , Y 2 k (k 1) dele svaku od stranica AB i CD konveksnog četvorougla ABCD na po 2 k + 1 jednakih 1 delova kao na slici. Tada je P(Xk Xk + 12 k. Y+k 1+ 1 Yk) = P(ABCD). C A Y 1 X 1 Yk Yk + 1 Xk Y 2 k D Xk + 1 X 2 k B 18

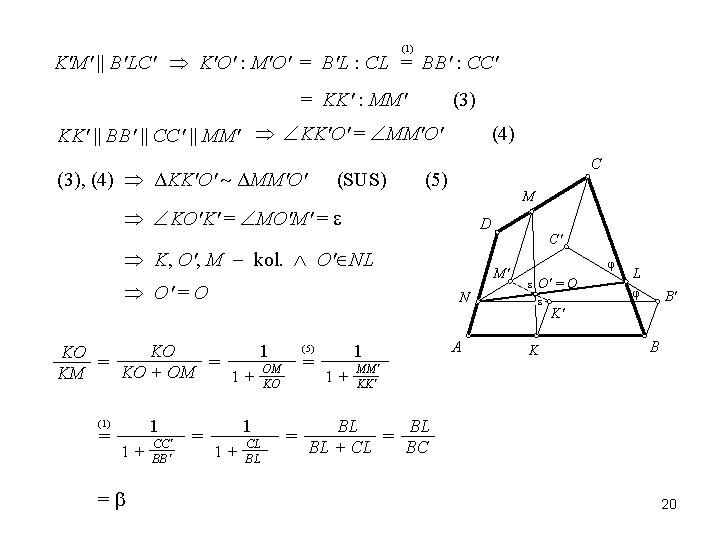
LEMA 1. Na stranicama AB, BC, CD, DA konveksnog četvorougla ABCD uočene su redom tačke K, L, M, N, takve da je AK : AB = DM : DC = i AN : AD = BL : BC = . Ako se duži KM i NL seku u tački O, tada je NO : NL = i KO : KM = . Dokaz. (I) ABB'N , DCC'N paralelogrami BB'L CC'L (SUS) (1) BLB' = CLC' = B', L, C' kolinearne K' NB' , KK' AN BB' M' NC' , MM' DN CC' NK' : NB' = AK : AB = α = DM : DC = NM' : NC' M K'M' || B'LC' K'M' NL = {O'} D (2) NO' : NL = NK' : NB' = α O' = O K, O', M kolinearne C (2) C' M' N φ O O' L φ B' K' A K B 19

(1) K'M' || B'LC' K'O' : M'O' = B'L : CL = BB' : CC' = KK' : MM' (3) KK' BB' CC' MM' KK'O' = MM'O' (3), (4) ΔKK'O' ΔMM'O' (SUS) (4) C (5) M KO'K' = MO'M' = D K, O', M kol. O' NL M' O' = O N KO 1 KO = = OM KO + OM KM 1 + KO 1 (1) = 1+ = CC' BB' = 1 1+ CL BL = A 1 (5) 1+ C' φ O' = O K L φ B' K' B MM' KK' BL BL = BL + CL = BC 20

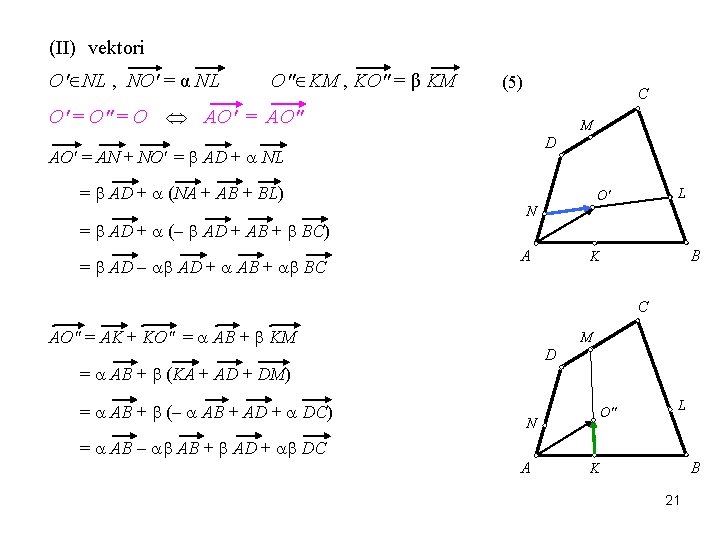
(II) vektori O' NL , NO' = α NL O" KM , KO" = β KM (5) C O' = O" = O AO' = AO" M D AO' = AN + NO' = AD + NL = AD + (NA + AB + BL) = AD + ( AD + AB + BC) = AD AD + AB + BC L O' N A B K C AO" = AK + KO" = AB + KM M D = AB + (KA + AD + DM) = AB + ( AB + AD + DC) O" N L = AB AB + AD + DC A B K 21

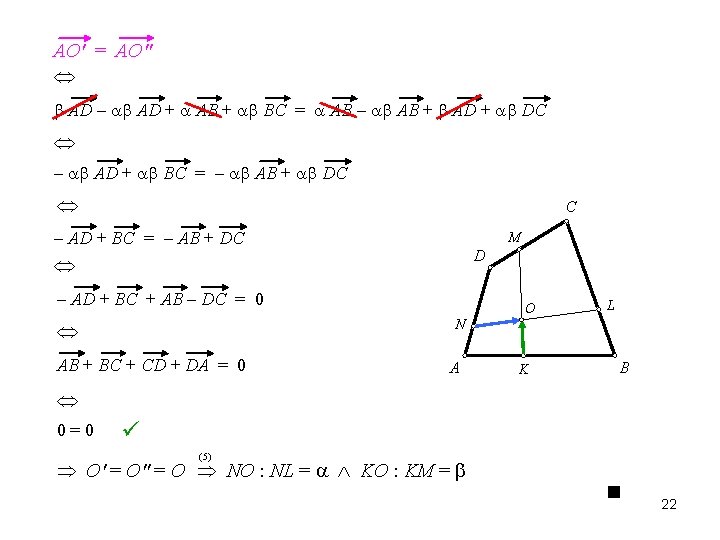
AO' = AO" AD AD + AB + BC = AB AB + AD + DC AD + BC = AB + DC C AD + BC = AB + DC M D AD + BC + AB DC = 0 O L N AB + BC + CD + DA = 0 A K B 0=0 (5) O' = O" = O NO : NL = KO : KM = 22

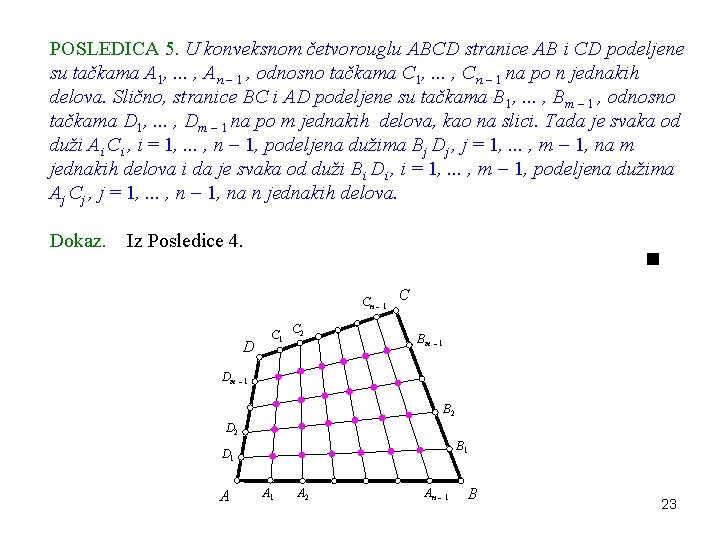
POSLEDICA 5. U konveksnom četvorouglu ABCD stranice AB i CD podeljene su tačkama A 1, . . . , An 1 , odnosno tačkama C 1, . . . , Cn 1 na po n jednakih delova. Slično, stranice BC i AD podeljene su tačkama B 1, . . . , Bm 1 , odnosno tačkama D 1, . . . , Dm 1 na po m jednakih delova, kao na slici. Tada je svaka od duži Ai Ci , i = 1, . . . , n 1, podeljena dužima Bj Dj , j = 1, . . . , m 1, na m jednakih delova i da je svaka od duži Bi Di , i = 1, . . . , m 1, podeljena dužima Aj Cj , j = 1, . . . , n 1, na n jednakih delova. Dokaz. Iz Posledice 4. Cn 1 D C 1 C 2 C Bm 1 Dm 1 B 2 D 2 B 1 D 1 A A 1 A 2 An 1 B 23

POSLEDICA 6. Neka je n neparan broj veći od 1. Svaka stranica konveksnog četvorougla ABCD podeljena n jednakih delova i odgovarjuće tačke spojene dužima kao na slici. Tada je površina "srednjeg" četvorougla jednaka 1 n 2 P(ABCD). Dokaz. Iz Posledica 4 i 5. Cn D C 1 1 C Bn 1 Dn 1 B 1 D 1 A A 1 An 1 B 24

PRIMER 10. Tačke K, L, M, N redom sredine stranica AB, BC, CD, DA konveksnog četvorougla ABCD i neka se duži KM i NL seku u tački O. Dokazati da je P(AKON) + P(CMOL) = P(BLOK) + P(DNOM). Dokaz. P 1 = P(AKO) Q 1 = P(KBO) P 2 = P(LCO) Q 2 = P(BLO) P 3 = P(CMO) Q 3 = P(MDO) P 4 = P(MDO) Q 4 = P(DNO) Posl. 3 Pi = Qi , i = 1, 2, 3, 4 D Q 3 N C M P 3 P 2 Q 4 O P 4 A Q 2 Q 1 P 1 (1) L B K P(AKON) + P(CMOL) = (P 1 + P 4) + (P 2 + P 3) (1) = (Q 1 + Q 4) + (Q 2 + Q 3) = (Q 1 + Q 2) + (Q 3 + Q 4) = P(BLOK) + P(DNOM) 25

POSLEDICA 7. Neka je m i n pozitivni parni brojevi. Stranice AB i CD konveksnog četvorougla ABCD podeljene su na po m jednakih delova, a stranice BC i AD na po n jednakih delova. Zatim su odgovarajuće tačke spojene dužima i dobijena polja obojena kao na slici. Tada je zbir površina belih polja jednak zbiru površina crvenih. Dokaz. Iz Primera 9. Cn 1 D C 1 C Bm 1 Dm 1 B 1 D 1 A A 1 An 1 B 26

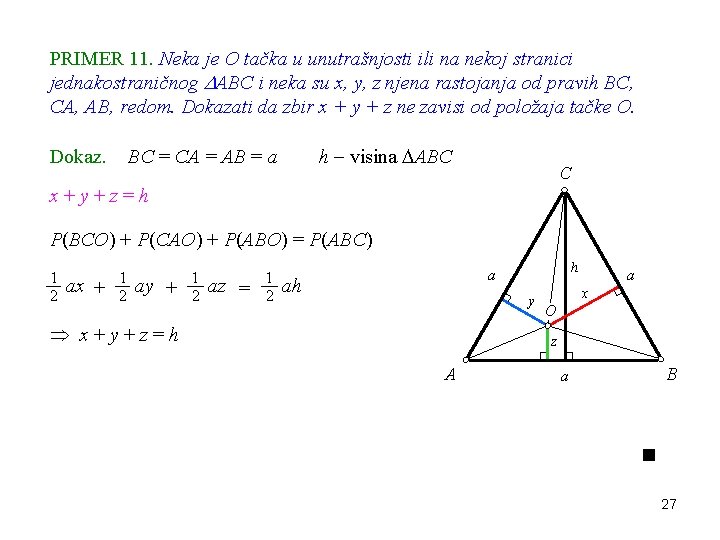
PRIMER 11. Neka je O tačka u unutrašnjosti ili na nekoj stranici jednakostraničnog ABC i neka su x, y, z njena rastojanja od pravih BC, CA, AB, redom. Dokazati da zbir x + y + z ne zavisi od položaja tačke O. Dokaz. h visina ABC BC = CA = AB = a C x+y+z=h P(BCO) + P(CAO) + P(ABO) = P(ABC) 1 2 ax + 1 2 ay + 1 2 az = 1 2 h a ah y x+y+z=h a x O z A B a 27

POSLEDICA 8. Proizvoljna tačka O koja pripada u unutrašnjosti pravilnog šestougla ABCDEF spojena je dužima s temenima šestougla i dobijeni trouglovi naizmenično obojeni kao na slici. Tada je zbir površina zelenih trouglova jednak zbiru površina belih. Dokaz. AB = BC = CD = DE = EF = EA = a P(ABO) + P(CDO) + P(EFO) = a 2 (x 1 + x 2 + x 3) P(BCO) + P(DEO) + P(FAO) = a 2 (y 1 + y 2 + y 3) X 1 X 2 X 3 Y 1 Y 2 Y 3 jednakostr. (str. 3 a) (3) Pr. 10 (1) (2) Y 1 E a = visina Y 1 Y 2 Y 3 x 3 (4) (1), (2), (4) P(ABO) + P(CDO) + P(EFO) = P(BCO) + P(DEO) + P(FAO) X 2 a O x 1 a A Y 3 a x 2 y 1 y 3 a a a y 2 F a D a a a (3) = y 1 + y 2 + y 3 a a x 1 + x 2 + x 3 = visina X 1 X 2 X 3 Pr. 10 X 1 C a a X 3 a B a a Y 2 28

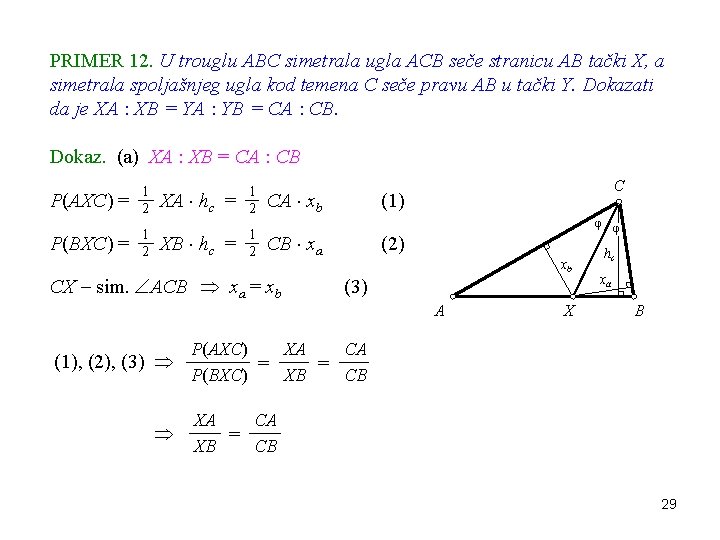
PRIMER 12. U trouglu ABC simetrala ugla ACB seče stranicu AB tački X, a simetrala spoljašnjeg ugla kod temena C seče pravu AB u tački Y. Dokazati da je XA : XB = YA : YB = CA : CB. Dokaz. (a) XA : XB = CA : CB P(AXC) = 1 2 P(BXC) = 1 2 XA hc = 1 2 CA xb XB hc = 1 2 CB xa CX sim. ACB xa = xb C (1) φ φ (2) xb (3) A (1), (2), (3) X hc xa B P(AXC) XA CA = = P(BXC) XB CB XA CA = XB CB 29

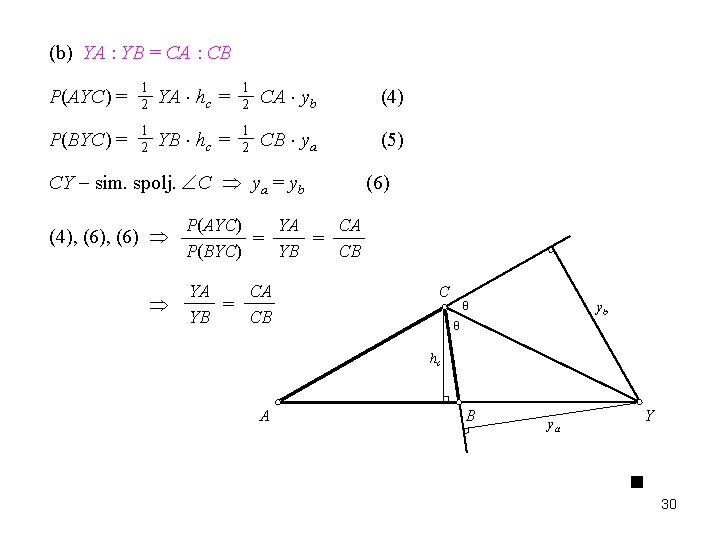
(b) YA : YB = CA : CB P(AYC) = 1 2 YA hc = 1 2 CA yb (4) P(BYC) = 1 2 YB hc = 1 2 CB ya (5) CY sim. spolj. C ya = yb (4), (6) (6) P(AYC) YA CA = = P(BYC) YB CB YA CA = YB CB C yb θ θ hc A B Y ya 30

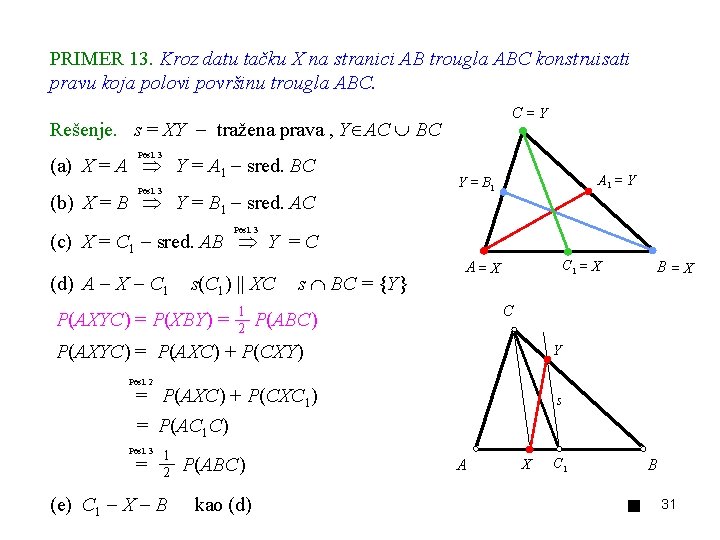
PRIMER 13. Kroz datu tačku X na stranici AB trougla ABC konstruisati pravu koja polovi površinu trougla ABC. C=Y Rešenje. s = XY tražena prava , Y AC BC Posl. 3 (a) X = A Y = A 1 sred. BC Posl. 3 (b) X = B Y = B 1 sred. AC A 1 = Y Y = B 1 Posl. 3 (c) X = C 1 sred. AB Y = C (d) A X C 1 s(C 1) || XC P(AXYC) = P(XBY) = 1 2 s BC = Y C 1 = X A= X B=X C P(ABC) P(AXYC) = P(AXC) + P(CXY) Y Posl. 2 = P(AXC) + P(CXC 1) s = P(AC 1 C) Posl. 3 = 1 2 (e) C 1 X B P(ABC) kao (d) A X C 1 B 31

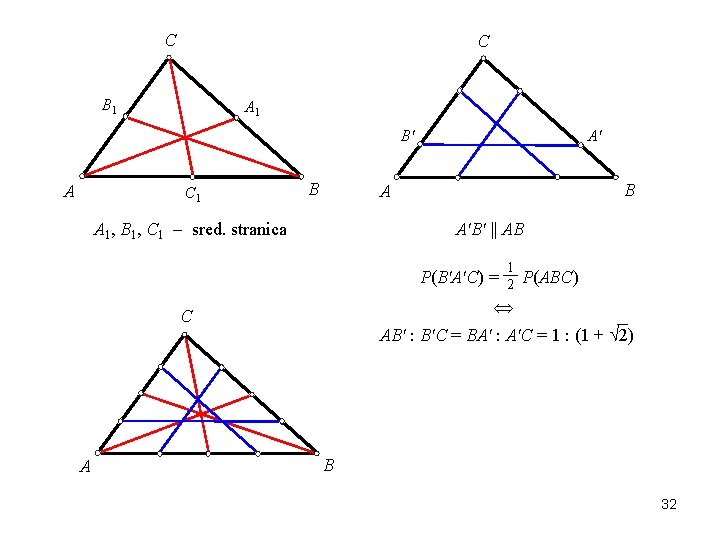
C C B 1 A 1 B' A C 1 B A' B A A 1, B 1, C 1 sred. stranica A'B' || AB P(B'A'C) = P(ABC) C A 1 2 AB' : B'C = BA' : A'C = 1 : (1 + 2) B 32

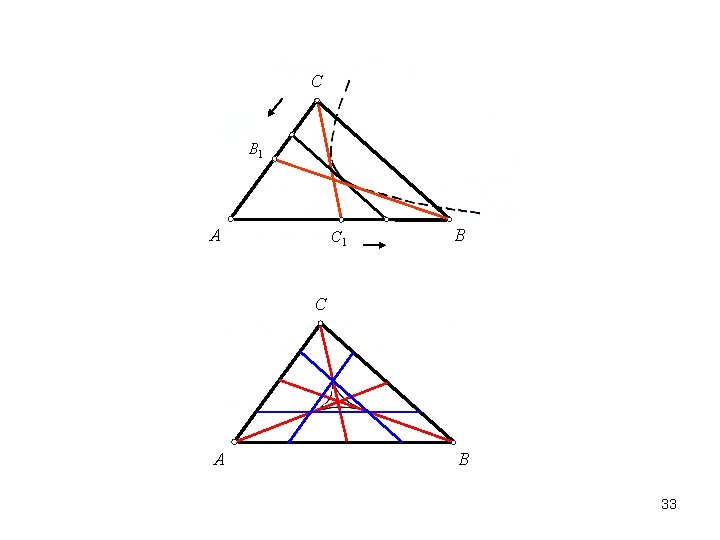
C B 1 A C 1 B C A B 33

PRIMER 14. Ako prava s polovi i obim i površinu ABC, dokazati da s prolazi kroz centar upisane kružnice u ABC. Dokaz. BC = a , CA = b , AB = c CX + CY = YA + AB + BX = P(YXC) = P(ABXY) s BC = {X} , s AC = {Y} a+b+c 2 (1) (2) s sim. C = {O} O centar up. kružn. u ΔABC r = r' 2 P(YXC) = (CX + CY)r C b γ 2 a Y (3) r r r' 2 P(ABXY) = 2(P(ABO) + P(BXO) + P(AYO)) = AB r' + BX r + AY r γ 2 (4) A O X B c (2), (3), (4) (CX + CY BX AY)r = AB r' (CX + CY (a CX) (b CY))r = cr' (1) (2(CX + CY) a b)r = cr' (a + b + c a b)r = cr' cr = cr' r = r' O centar up. kružn. u ΔABC 34 s

POSLEDICA 9. Neka je s prava koja prolazi kroz centar upisane kružnice u ΔABC. Ako s polovi obim trougla, tada ona polovi i njegovu površinu i obratno. Dokaz. Kao u primeru 13. 35

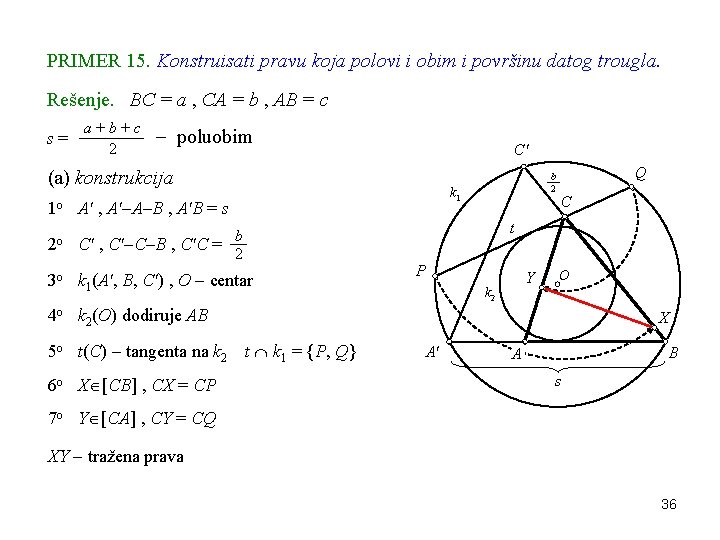
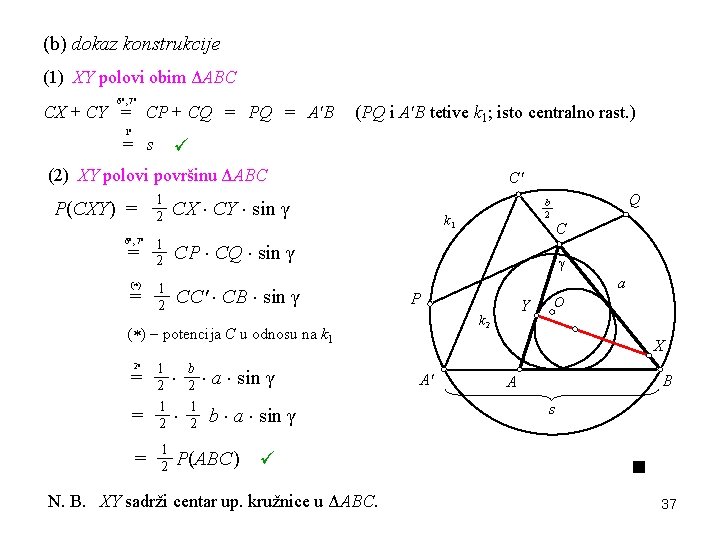
PRIMER 15. Konstruisati pravu koja polovi i obim i površinu datog trougla. Rešenje. BC = a , CA = b , AB = c s= a+b+c 2 poluobim C' (a) konstrukcija 1 o A' , A' A B , A'B = s 2 o b C' , C' C B , C'C = 2 3 o k 1(A', B, C') , O centar Q b 2 k 1 C t P Y k 2 O 4 o k 2(O) dodiruje AB 5 o t(C) tangenta na k 2 t k 1 = {P, Q} 6 o X [CB] , CX = CP X A' B A s 7 o Y [CA] , CY = CQ XY tražena prava 36

(b) dokaz konstrukcije (1) XY polovi obim ΔABC 6 o, 7 o CX + CY = CP + CQ = PQ = A'B 1 o = s (PQ i A'B tetive k 1; isto centralno rast. ) (2) XY polovi površinu ΔABC P(CXY) = 6 o, 7 o = ( ) = 1 2 CX CY sin γ 1 2 CP CQ sin γ 1 2 CC' CB sin γ C' k 1 = 1 2 b 2 = 1 2 P(ABC) a sin γ b a sin γ N. B. XY sadrži centar up. kružnice u ΔABC. C γ a P Y k 2 ( ) potencija C u odnosu na k 1 2 o Q b 2 O X A' B A s 37

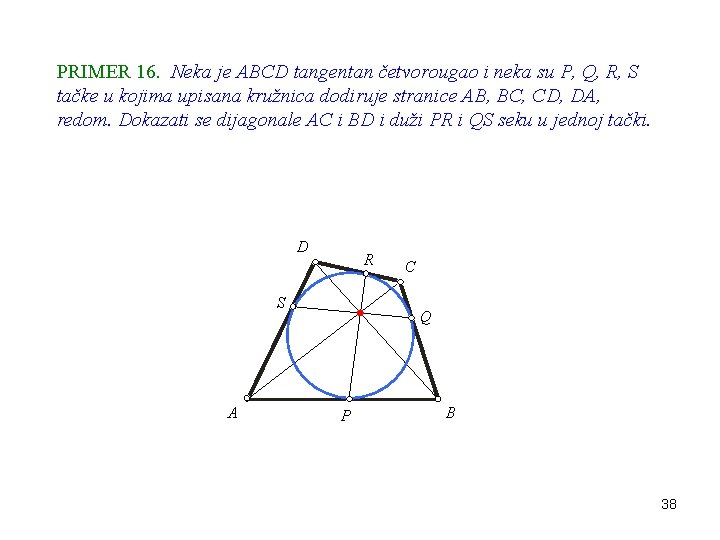
PRIMER 16. Neka je ABCD tangentan četvorougao i neka su P, Q, R, S tačke u kojima upisana kružnica dodiruje stranice AB, BC, CD, DA, redom. Dokazati se dijagonale AC i BD i duži PR i QS seku u jednoj tački. D R S A C Q P B 38

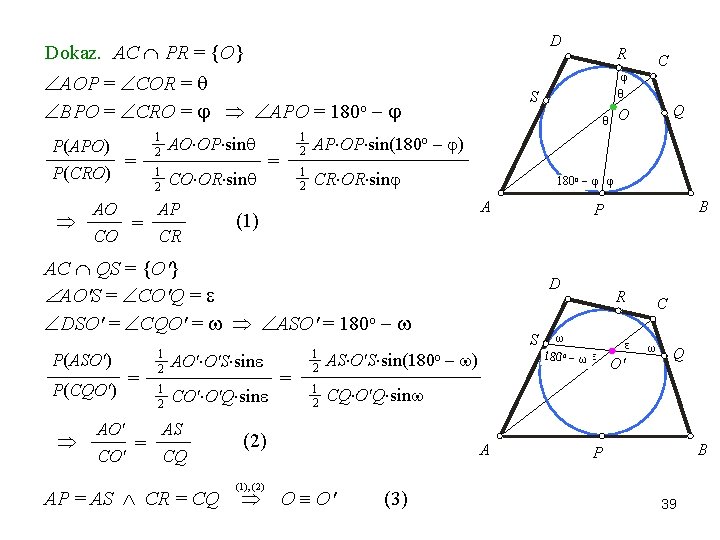
D Dokaz. AC PR = {O} AOP = COR = BPO = CRO = APO = 180 o P(APO) = P(CRO) 1 2 AO OP sin 1 2 CO OR sin AO AP = CO CR = AP OP sin(180 o ) 1 2 CR OR sin 180 o φ φ A AC QS = {O'} AO'S = CO'Q = DSO' = CQO' = ASO' = 180 o P(ASO') P(CQO') = AO' O'S sin 1 2 CO' O'Q sin AO' AS = CO' CQ AP = AS CR = CQ = 1 2 AS O'S sin(180 o 1 2 CQ O'Q sin (2) (1), (2) S ) (3) B P D A O O' Q O θ 1 2 C φ θ S (1) 1 2 R R ω 180 o ω ε ε O' C ω Q B P 39

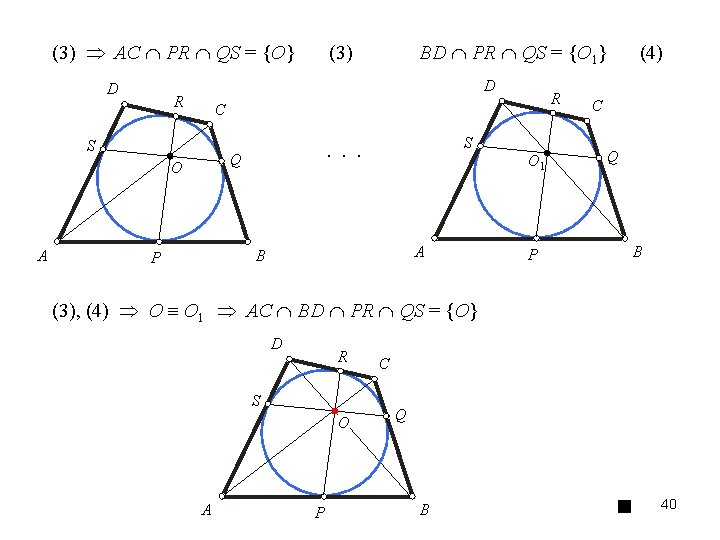
(3) AC PR QS = {O} D D R R C S S . . . Q O A BD PR QS = {O 1} (3) O 1 A B P (4) C Q B P (3), (4) O O 1 AC BD PR QS = {O} D R S O A P C Q B 40

PRIMER 17. (Njutn) Dokazati da sredine dijagonala tangentnog četvorougla i centar upisane kružnice pripadaju jednoj pravoj. D C K O A L B Dokaz. ABCD tangentan K , L sred. AC , BD O centar upisane kružn. D C (a) ABCD paralelogram (romb) K=L=O A B 41

(b) ABCD nije pralelogram AB || CD PABCD = P D K sred. AC P(ABK) = P(BCK) = P 1 P(ADK) = P(CDK) = P 2 P(ABK) + P(CDK) = P 1 + P 2 = 1 2 C P 2 P (1) K P 1 A L sred. BD D P(ABL) = P(ADL) = P 3 P(BCL) = P(CDL) = P 4 P(ABL) + P(ADL) = P 3 + P 4 = B 1 2 P P 3 L (2) C P 4 P 3 A B 42

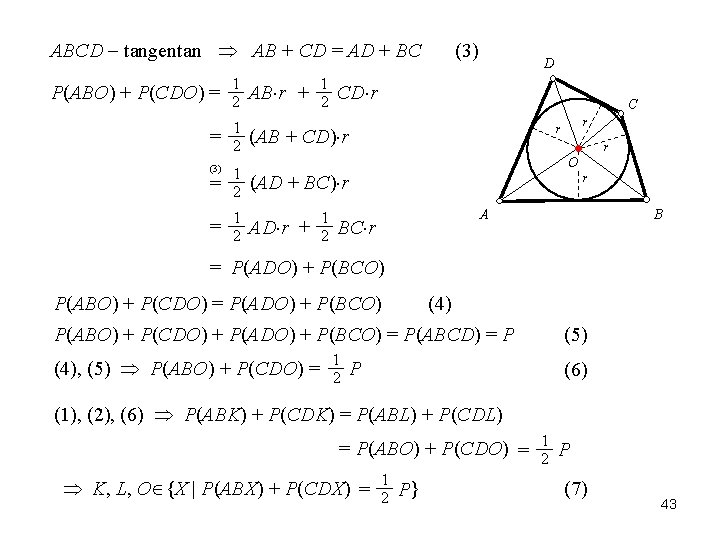
ABCD tangentan AB + CD = AD + BC P(ABO) + P(CDO) = 1 2 (3) = 1 2 AB r + 1 2 (3) D CD r C r r (AB + CD) r r O r (AD + BC) r AD r + 1 2 A BC r B = P(ADO) + P(BCO) P(ABO) + P(CDO) = P(ADO) + P(BCO) (4) P(ABO) + P(CDO) + P(ADO) + P(BCO) = P(ABCD) = P (4), (5) P(ABO) + P(CDO) = 1 2 (5) P (6) (1), (2), (6) P(ABK) + P(CDK) = P(ABL) + P(CDL) = P(ABO) + P(CDO) = K, L, O {X | P(ABX) + P(CDX) = 1 2 P} 1 2 P (7) 43

ABCD proizvoljan četvorougao , AB || CD , AB CD = {S} 1 2 GMT = {X int ABCD | P(ABX) + P(CDX) = X GMT P(ABX) + P(CDX) = 1 2 P P} = ? (8) P = P(ABCD) D C l A'S = AB , D'S = DC X P(ABX) = P(A'SX) P(CDX) = P(SD'X) (8) P(A'SX) + P(SD'X) = 1 2 P' P P(A'SD'X) = P(A'SX) + P(SD'X) = P(A'SD') + P(A'D'X) D' A 1 2 P S A' (9) P(A'SD') = P' = const. (9), (10) P(A'D'X) = P(A'SD'X) P(A'SD') = X int ABCD X l , l || A'D' B 1 2 (10) P P' = const. (11) (7), (11) K, L, O l K, L, O kolinearne 44

K, L, O int ABCD P(ABK) + P(CDK) = P(ABL) + P(CDL) = P(ABO) + P(CDO) = 1 2 P K, L, O l K, L, O kolinearne D C K A O l L B 45