Structural Equation Modeling SEM Essentials Purpose of this

Structural Equation Modeling (SEM) Essentials Purpose of this module is to provide a very brief presentation of the things one needs to know about SEM before learning how apply SEM. by Jim Grace 1

Where You can Learn More about SEM Grace (2006) Structural Equation Modeling and Natural Systems. Cambridge Univ. Press. Shipley (2000) Cause and Correlation in Biology. Cambridge Univ. Press. Kline (2005) Principles and Practice of Structural Equation Modeling. (2 nd Edition) Guilford Press. Bollen (1989) Structural Equations with Latent Variables. John Wiley and Sons. Lee (2007) Structural Equation Modeling: A Bayesian Approach. John Wiley and Sons. 2

Outline I. Essential Points about SEM II. Structural Equation Models: Form and Function 3

I. SEM Essentials: 1. SEM is a form of graphical modeling, and therefore, a system in which relationships can be represented in either graphical or equational form graphical form y 1 = γ 11 x 1 + ζ 1 x 1 1 y 1 2. An equation is said to be structural if there exists sufficient evidence from all available sources to support the interpretation that x 1 has a causal effect on y 1. 4

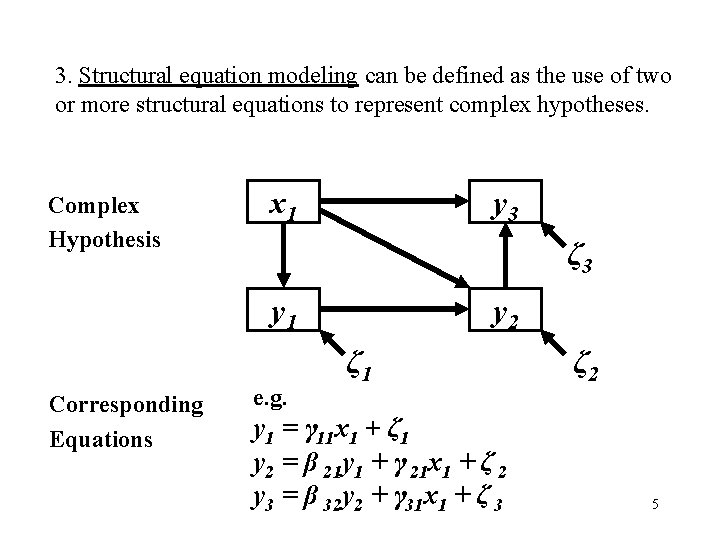
3. Structural equation modeling can be defined as the use of two or more structural equations to represent complex hypotheses. Complex Hypothesis x 1 y 3 ζ 3 y 1 Corresponding Equations e. g. y 2 ζ 1 y 1 = γ 11 x 1 + ζ 1 y 2 = β 21 y 1 + γ 21 x 1 + ζ 2 y 3 = β 32 y 2 + γ 31 x 1 + ζ 3 ζ 2 5

4. Some practical criteria for supporting an assumption of causal relationships in structural equations: a. manipulations of x can repeatably be demonstrated to be followed by responses in y, and/or b. we can assume that the values of x that we have can serve as indicators for the values of x that existed when effects on y were being generated, and/or c. if it can be assumed that a manipulation of x would result in a subsequent change in the values of y Relevant References: Pearl (2000) Causality. Cambridge University Press. Shipley (2000) Cause and Correlation in Biology. Cambridge 6

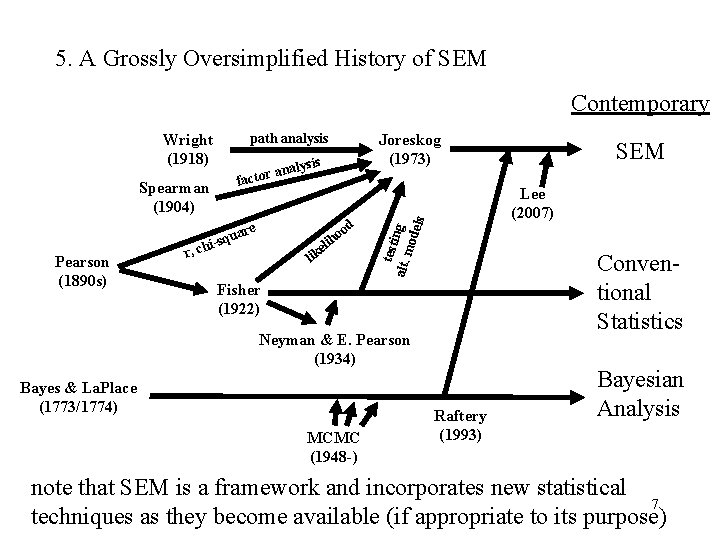
5. A Grossly Oversimplified History of SEM Contemporary path analysis Wright (1918) alysis n a r to fac d re oo h i l ke ua i-sq r, ch li Conventional Statistics Fisher (1922) Neyman & E. Pearson (1934) Bayes & La. Place (1773/1774) MCMC (1948 -) SEM Lee (2007) test alt. ing mod els Spearman (1904) Pearson (1890 s) Joreskog (1973) Raftery (1993) Bayesian Analysis note that SEM is a framework and incorporates new statistical 7 techniques as they become available (if appropriate to its purpose)

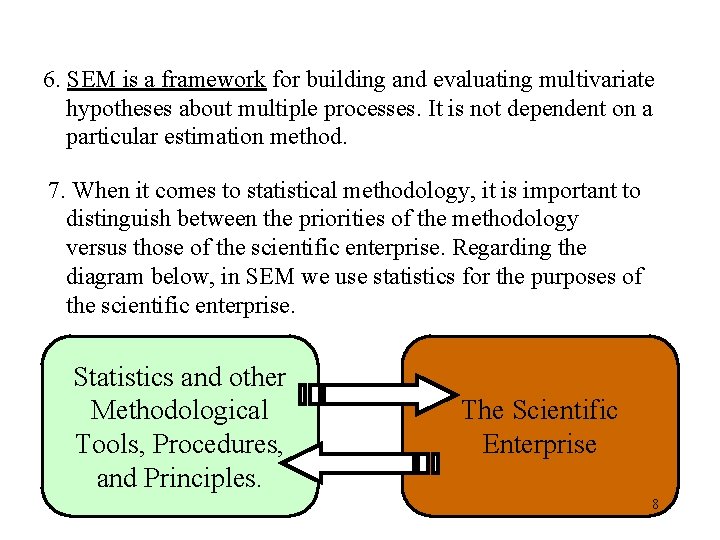
6. SEM is a framework for building and evaluating multivariate hypotheses about multiple processes. It is not dependent on a particular estimation method. 7. When it comes to statistical methodology, it is important to distinguish between the priorities of the methodology versus those of the scientific enterprise. Regarding the diagram below, in SEM we use statistics for the purposes of the scientific enterprise. Statistics and other Methodological Tools, Procedures, and Principles. The Scientific Enterprise 8

The Methodological Side of SEM 9

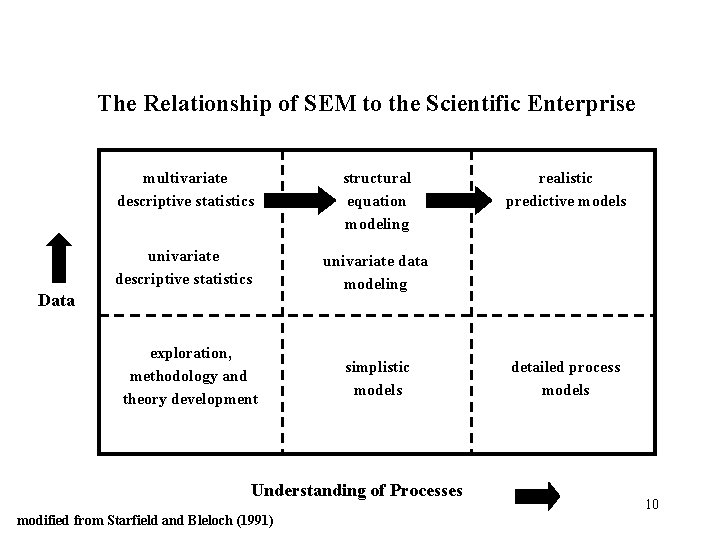
The Relationship of SEM to the Scientific Enterprise multivariate descriptive statistics structural equation modeling univariate descriptive statistics univariate data modeling Data exploration, methodology and theory development simplistic models Understanding of Processes modified from Starfield and Bleloch (1991) realistic predictive models detailed process models 10

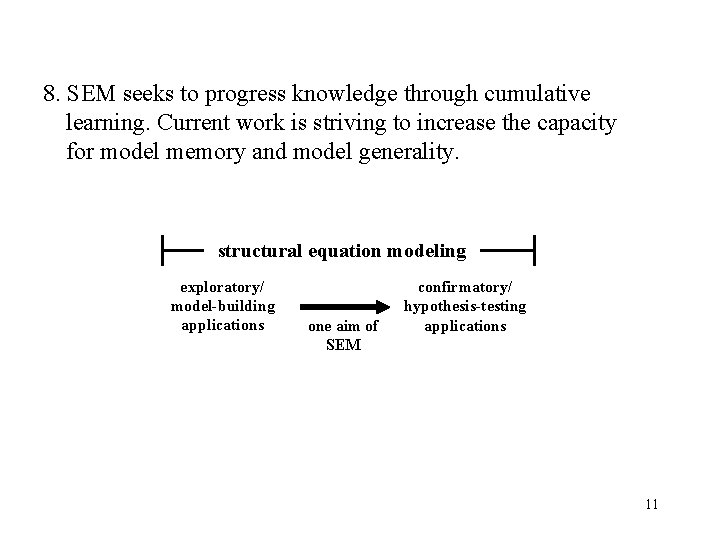
8. SEM seeks to progress knowledge through cumulative learning. Current work is striving to increase the capacity for model memory and model generality. structural equation modeling exploratory/ model-building applications one aim of SEM confirmatory/ hypothesis-testing applications 11

9. It is not widely understood that the univariate model, and especially ANOVA, is not well suited for studying systems, but rather, is designed for studying individual processes, net effects, or for identifying predictors. 10. The dominance of the univariate statistical model in the natural sciences has, in my personal view, retarded the progress of science. 12

11. An interest in systems under multivariate control motivates us to explicitly consider the relative importances of multiple processes and how they interact. We seek to consider simultaneously the main factors that determine how system responses behave. 12. SEM is one of the few applications of statistical inference where the results of estimation are frequently “you have the wrong model!”. This feedback comes from the unique feature that in SEM we compare patterns in the data to those implied by the model. This is an extremely important form of learning about systems. 13

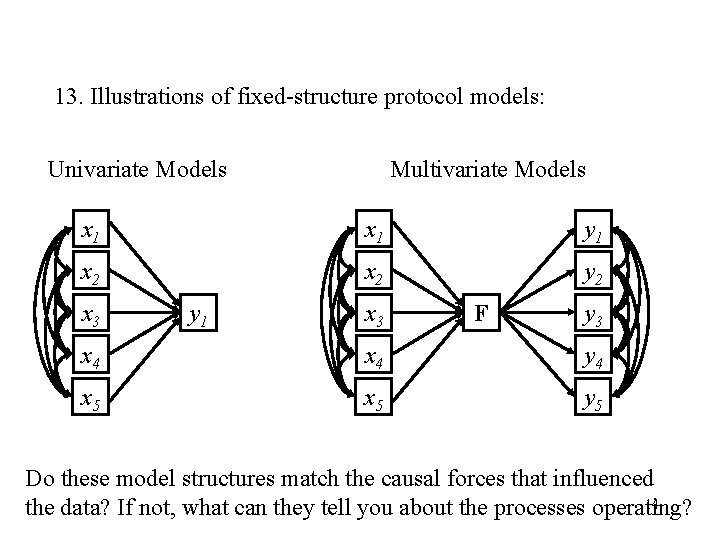
13. Illustrations of fixed-structure protocol models: Univariate Models Multivariate Models x 1 y 1 x 2 y 2 x 3 y 1 x 3 F y 3 x 4 y 4 x 5 y 5 Do these model structures match the causal forces that influenced 14 the data? If not, what can they tell you about the processes operating?

14. Structural equation modeling and its associated scientific goals represent an ambitious undertaking. We should be both humbled by the limits of our successes and inspired by the learning that takes place during the journey. 15

II. Structural Equation Models: Form and Function A. Anatomy of Observed Variable Models 16

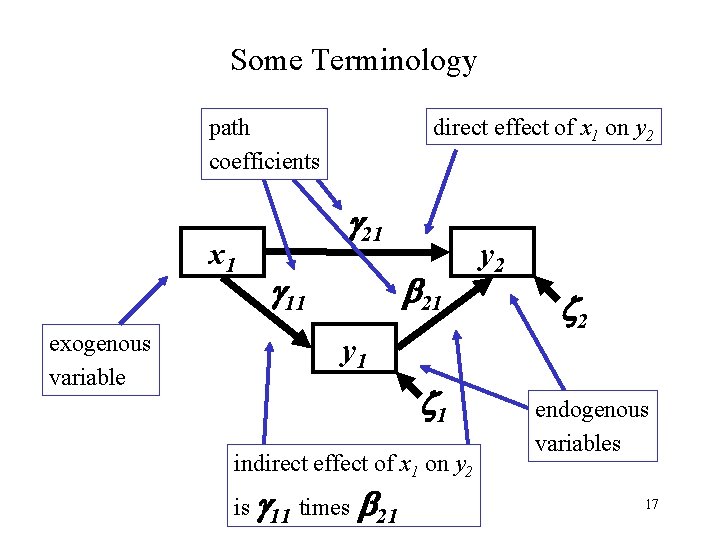
Some Terminology path coefficients x 1 exogenous variable direct effect of x 1 on y 2 21 11 21 y 1 1 indirect effect of x 1 on y 2 is 11 times 21 y 2 2 endogenous variables 17

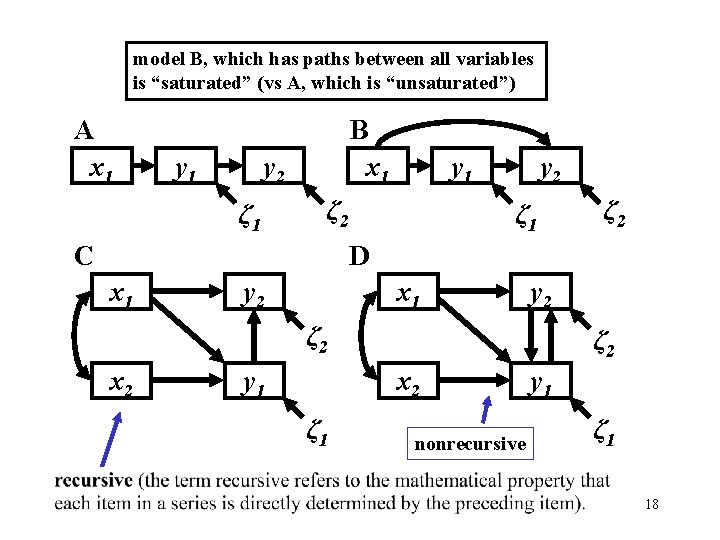
model B, which has paths between all variables is “saturated” (vs A, which is “unsaturated”) A x 1 y 1 B x 1 y 2 ζ 1 y 1 ζ 2 C y 2 ζ 1 ζ 2 D x 1 y 2 ζ 2 x 2 y 1 ζ 2 x 2 ζ 1 nonrecursive y 1 ζ 1 18

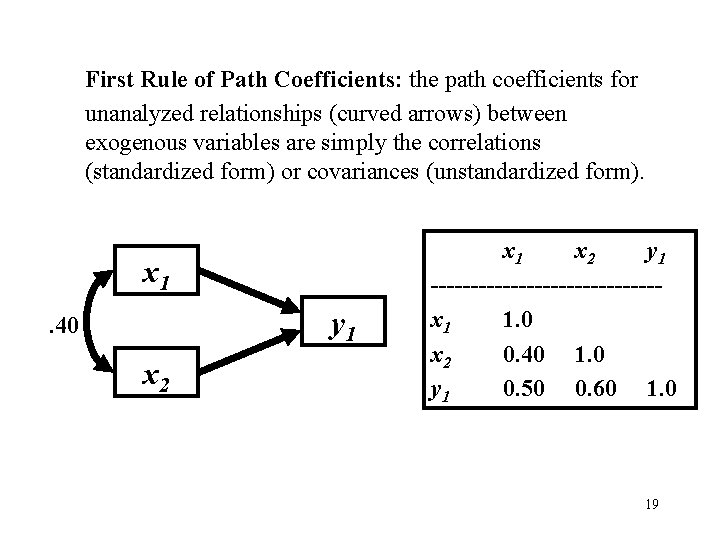
First Rule of Path Coefficients: the path coefficients for unanalyzed relationships (curved arrows) between exogenous variables are simply the correlations (standardized form) or covariances (unstandardized form). x 1 y 1 . 40 x 2 x 1 x 2 y 1 --------------x 1 1. 0 x 2 0. 40 1. 0 y 1 0. 50 0. 60 1. 0 19

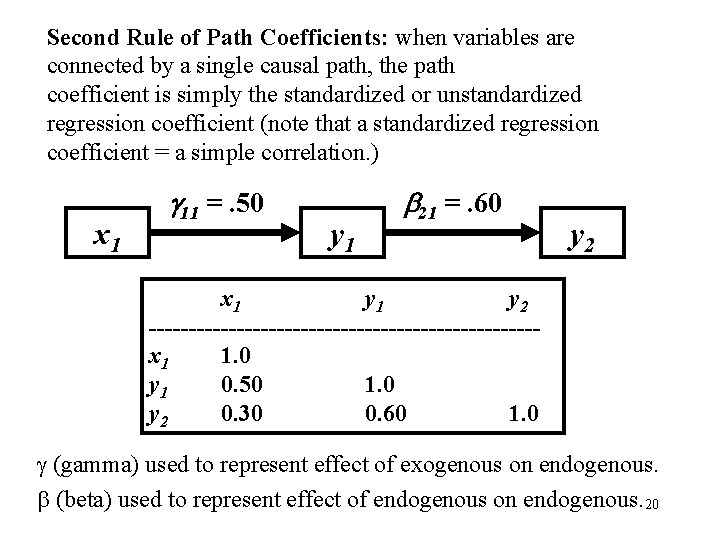
Second Rule of Path Coefficients: when variables are connected by a single causal path, the path coefficient is simply the standardized or unstandardized regression coefficient (note that a standardized regression coefficient = a simple correlation. ) x 1 11 =. 50 y 1 21 =. 60 y 2 x 1 y 2 ------------------------x 1 1. 0 y 1 0. 50 1. 0 y 2 0. 30 0. 60 1. 0 (gamma) used to represent effect of exogenous on endogenous. (beta) used to represent effect of endogenous on endogenous. 20

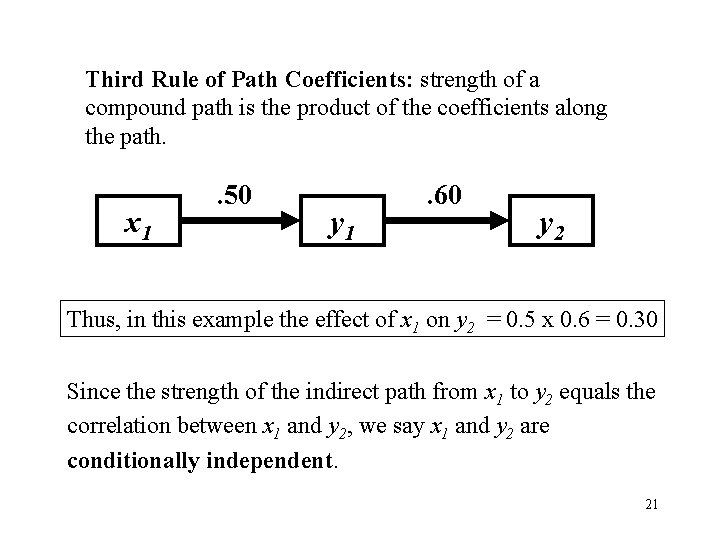
Third Rule of Path Coefficients: strength of a compound path is the product of the coefficients along the path. x 1 . 50 y 1 . 60 y 2 Thus, in this example the effect of x 1 on y 2 = 0. 5 x 0. 6 = 0. 30 Since the strength of the indirect path from x 1 to y 2 equals the correlation between x 1 and y 2, we say x 1 and y 2 are conditionally independent. 21

What does it mean when two separated variables are not conditionally independent? x 1 y 2 ------------------------x 1 1. 0 y 1 0. 55 1. 0 y 2 0. 50 0. 60 1. 0 x 1 r =. 55 y 1 r =. 60 y 2 0. 55 x 0. 60 = 0. 33, which is not equal to 0. 50 22

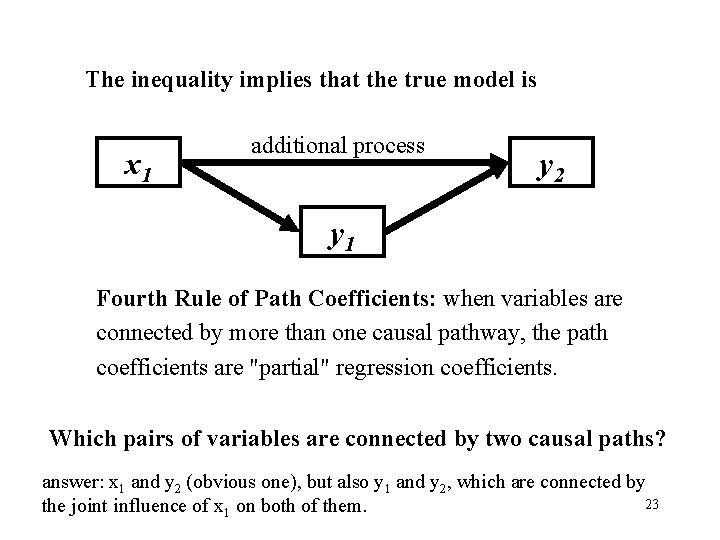
The inequality implies that the true model is x 1 additional process y 2 y 1 Fourth Rule of Path Coefficients: when variables are connected by more than one causal pathway, the path coefficients are "partial" regression coefficients. Which pairs of variables are connected by two causal paths? answer: x 1 and y 2 (obvious one), but also y 1 and y 2, which are connected by 23 the joint influence of x 1 on both of them.

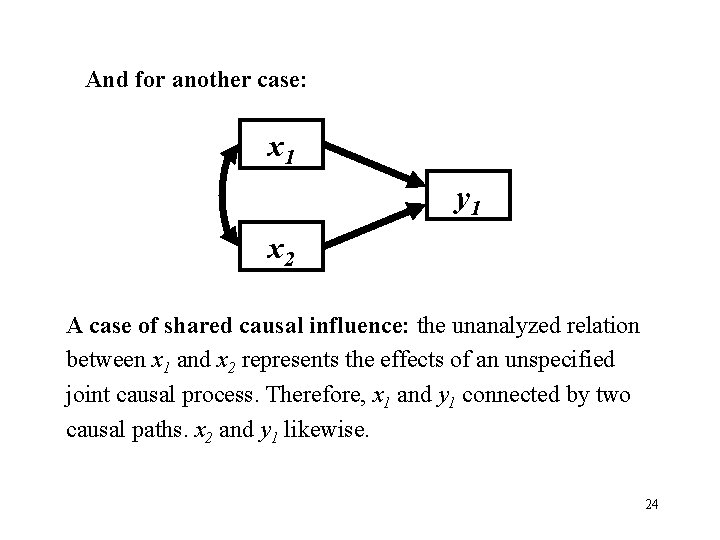
And for another case: x 1 y 1 x 2 A case of shared causal influence: the unanalyzed relation between x 1 and x 2 represents the effects of an unspecified joint causal process. Therefore, x 1 and y 1 connected by two causal paths. x 2 and y 1 likewise. 24

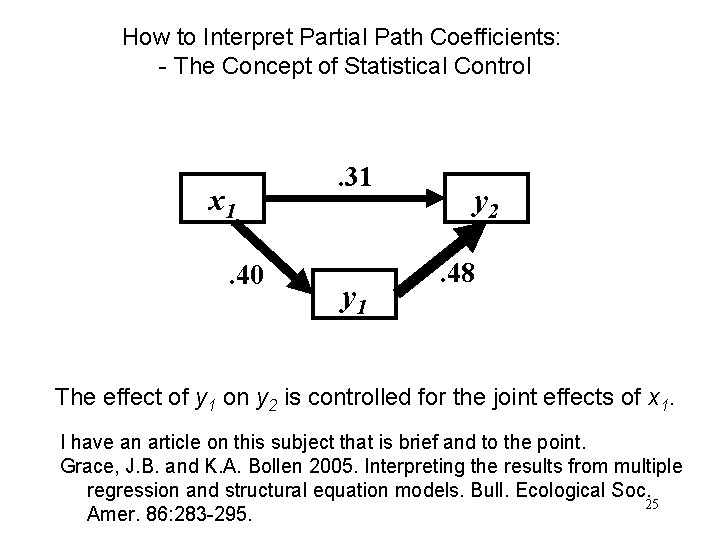
How to Interpret Partial Path Coefficients: - The Concept of Statistical Control x 1. 40 . 31 y 2. 48 The effect of y 1 on y 2 is controlled for the joint effects of x 1. I have an article on this subject that is brief and to the point. Grace, J. B. and K. A. Bollen 2005. Interpreting the results from multiple regression and structural equation models. Bull. Ecological Soc. 25 Amer. 86: 283 -295.

Interpretation of Partial Coefficients Analogy to an electronic equalizer from Sourceforge. net With all other variables in model held to their means, how much does a response variable change when a predictor is varied? 26

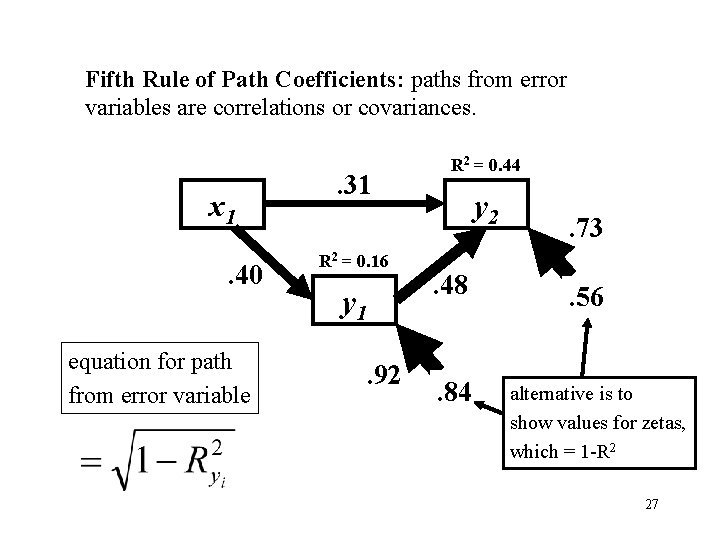
Fifth Rule of Path Coefficients: paths from error variables are correlations or covariances. x 1. 40 equation for path from error variable . 31 R 2 = 0. 16 y 1. 92 R 2 = 0. 44 y 2. 48 1. 84 . 73 2. 56 alternative is to show values for zetas, which = 1 -R 2 27

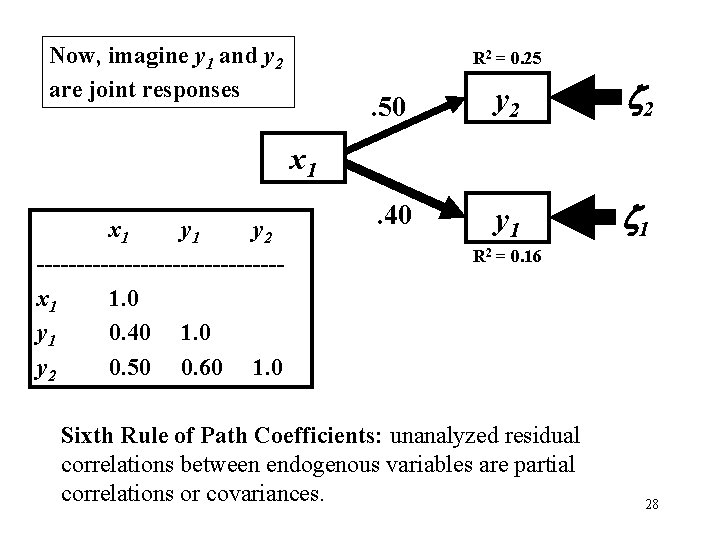
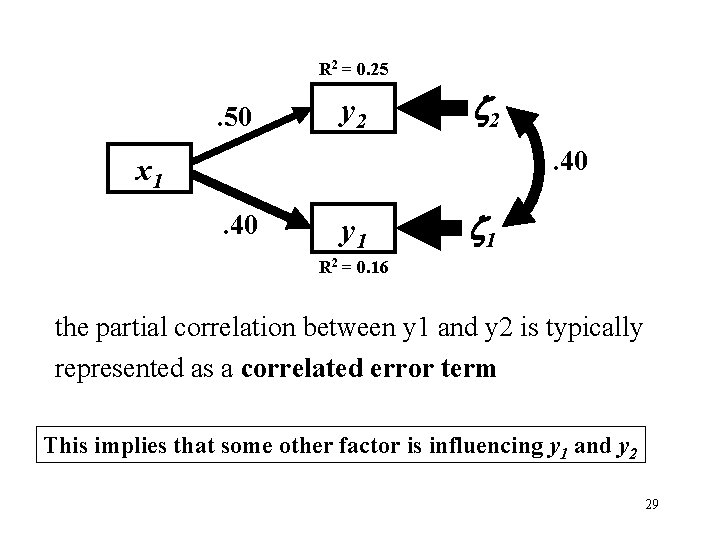
Now, imagine y 1 and y 2 are joint responses R 2 = 0. 25 . 50 y 2 2 . 40 y 1 1 x 1 y 2 ---------------x 1 1. 0 y 1 0. 40 1. 0 y 2 0. 50 0. 60 1. 0 R 2 = 0. 16 Sixth Rule of Path Coefficients: unanalyzed residual correlations between endogenous variables are partial correlations or covariances. 28

R 2 = 0. 25 . 50 y 2 2. 40 x 1. 40 y 1 1 R 2 = 0. 16 the partial correlation between y 1 and y 2 is typically represented as a correlated error term This implies that some other factor is influencing y 1 and y 2 29

Seventh Rule of Path Coefficients: total effect one variable has on another equals the sum of its direct and indirect effects. x 1 . 15. 64 . 80 x 2 -. 11 y 2. 27 ζ 2 y 1 Total Effects: x 1 x 2 y 1 ---------------y 1 0. 64 -0. 11 --y 2 0. 32 -0. 03 0. 27 ζ 1 Eighth Rule of Path Coefficients: sum of all pathways between two variables (causal and noncausal) equals the correlation/covariance. note: correlation between x 1 and y 1 = 0. 55, which equals 0. 64 - 0. 80*0. 11 30

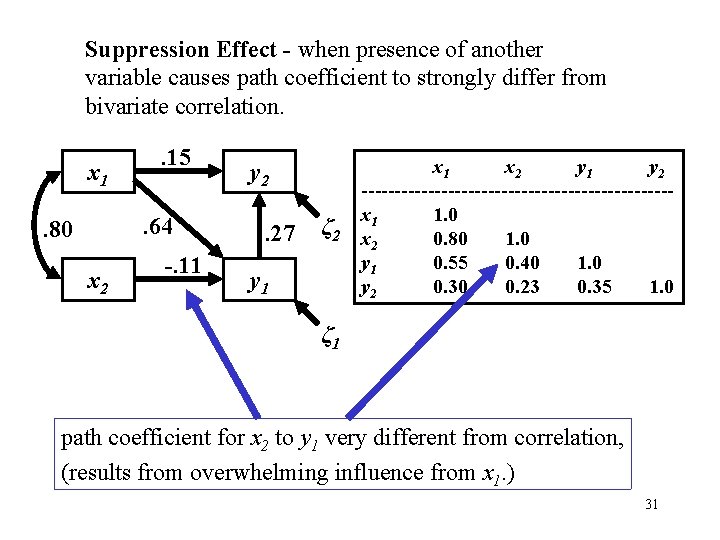
Suppression Effect - when presence of another variable causes path coefficient to strongly differ from bivariate correlation. x 1 . 15. 64 . 80 x 2 -. 11 y 2. 27 ζ 2 y 1 x 2 y 1 y 2 -----------------------x 1 1. 0 x 2 0. 80 1. 0 y 1 0. 55 0. 40 1. 0 y 2 0. 30 0. 23 0. 35 1. 0 ζ 1 path coefficient for x 2 to y 1 very different from correlation, (results from overwhelming influence from x 1. ) 31

II. Structural Equation Models: Form and Function B. Anatomy of Latent Variable Models 32

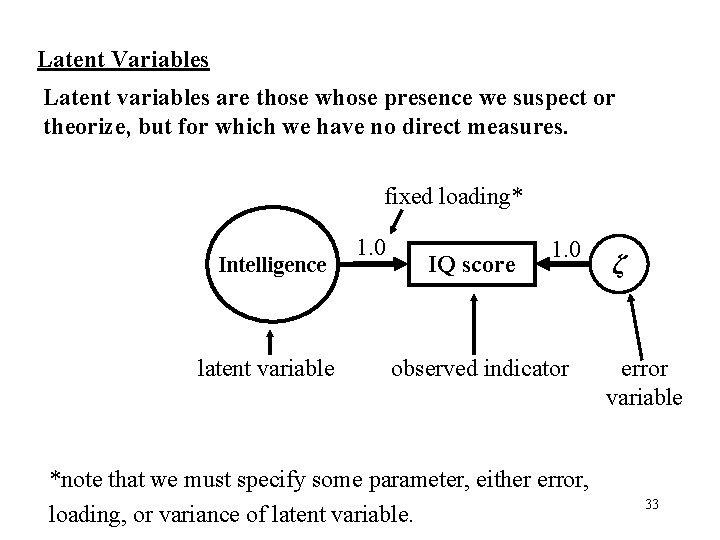
Latent Variables Latent variables are those whose presence we suspect or theorize, but for which we have no direct measures. fixed loading* Intelligence latent variable 1. 0 IQ score 1. 0 observed indicator *note that we must specify some parameter, either error, loading, or variance of latent variable. ζ error variable 33

Latent Variables (cont. ) Purposes Served by Latent Variables: (1) Specification of difference between observed data and processes of interest. (2) Allow us to estimate and correct for measurement error. (3) Represent certain kinds of hypotheses. 34

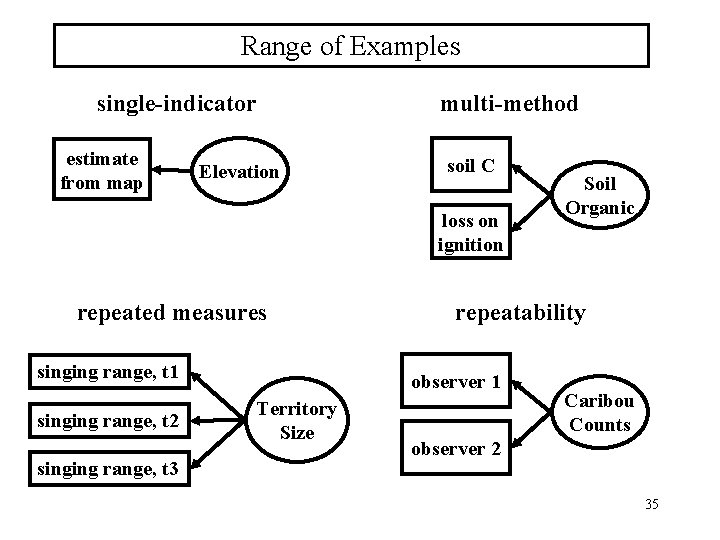
Range of Examples single-indicator estimate from map Elevation multi-method soil C loss on ignition repeated measures singing range, t 1 singing range, t 2 singing range, t 3 repeatability observer 1 Territory Size Soil Organic Caribou Counts observer 2 35

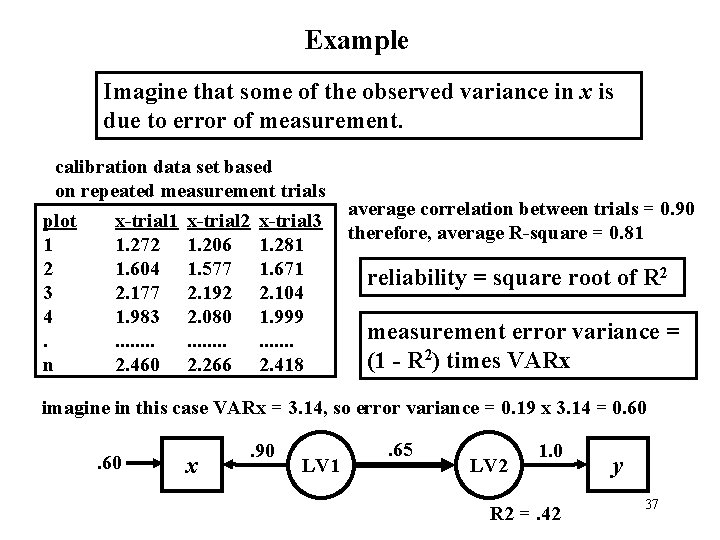
The Concept of Measurement Error the argument for universal use of latent variables 1. Observed variable models, path or other, assume all independent variables are measured without error. 2. Reliability - the degree to which a measurement is repeatable (i. e. , a measure of precision). illustration y x 0. 60 y R 2 = 0. 30 x error in measuring x is ascribed to error in predicting/explaining y 36

Example Imagine that some of the observed variance in x is due to error of measurement. calibration data set based on repeated measurement trials plot x-trial 1 x-trial 2 x-trial 3 1 1. 272 1. 206 1. 281 2 1. 604 1. 577 1. 671 3 2. 177 2. 192 2. 104 4 1. 983 2. 080 1. 999. . . n 2. 460 2. 266 2. 418 average correlation between trials = 0. 90 therefore, average R-square = 0. 81 reliability = square root of R 2 measurement error variance = (1 - R 2) times VARx imagine in this case VARx = 3. 14, so error variance = 0. 19 x 3. 14 = 0. 60 x . 90 LV 1 . 65 LV 2 1. 0 R 2 =. 42 y 37

II. Structural Equation Models: Form and Function C. Estimation and Evaluation 38

1. The Multiequational Framework (a) the observed variable model We can model the interdependences among a set of predictors and responses using an extension of the general linear model that accommodates the dependences of response variables on other response variables. y = α + Βy + Γx + ζ α = p x 1 vector of intercepts Φ = cov (x) = q x q matrix of covariances among xs Β = p x p coefficient matrix of ys on ys Ψ = cov (ζ) = q x q matrix of y = p x 1 vector of responses Γ = p x q coefficient matrix of ys on xs covariances among errors x = q x 1 vector of exogenous predictors ζ = p x 1 vector of errors for the elements of y 39

(b) the latent variable model η = α + Β η + Γξ + ζ The LISREL Equations Jöreskög 1973 where: η is a vector of latent responses, ξ is a vector of latent predictors, Β and Γ are matrices of coefficients, ζ is a vector of errors for η, and α is a vector of intercepts for η (c) the measurement model x = Λxξ + δ y = Λyη + ε where: Λx is a vector of loadings that link observed x variables to latent predictors, Λy is a vector of loadings that link observed y variables to latent responses, and δ and ε are vectors are errors 40

2. Estimation Methods (a) decomposition of correlations (original path analysis) (b) least-squares procedures (historic or in special cases) (c) maximum likelihood (standard method) (d) Markov chain Monte Carlo (MCMC) methods (including Bayesian applications) 41

Bayesian References: Bayesian SEM: Lee, SY (2007) Structural Equation Modeling: A Bayesian Approach. Wiley & Sons. Bayesian Networks: Neopolitan, R. E. (2004). Learning Bayesian Networks. Upper Saddle River, NJ, Prentice Hall Publs. 42

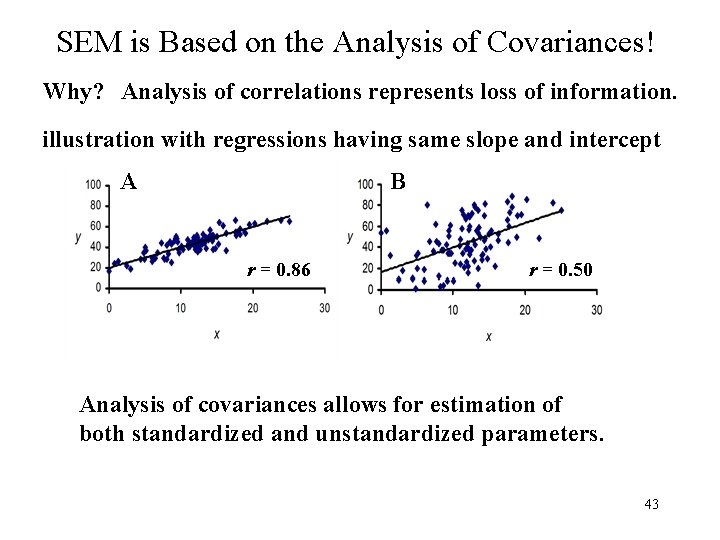
SEM is Based on the Analysis of Covariances! Why? Analysis of correlations represents loss of information. illustration with regressions having same slope and intercept A B r = 0. 86 r = 0. 50 Analysis of covariances allows for estimation of both standardized and unstandardized parameters. 43

2. Estimation (cont. ) – analysis of covariance structure The most commonly used method of estimation over the past 3 decades has been through the analysis of covariance structure (think – analysis of patterns of correlations among variables). compare Observed Correlations* S = { } 1. 0. 24 1. 0. 01. 70 1. 0 Model-Implied Correlations Σ = { } σ11 σ12 σ22 σ13 σ23 σ33 * typically the unstandardized correlations, or covariances 44

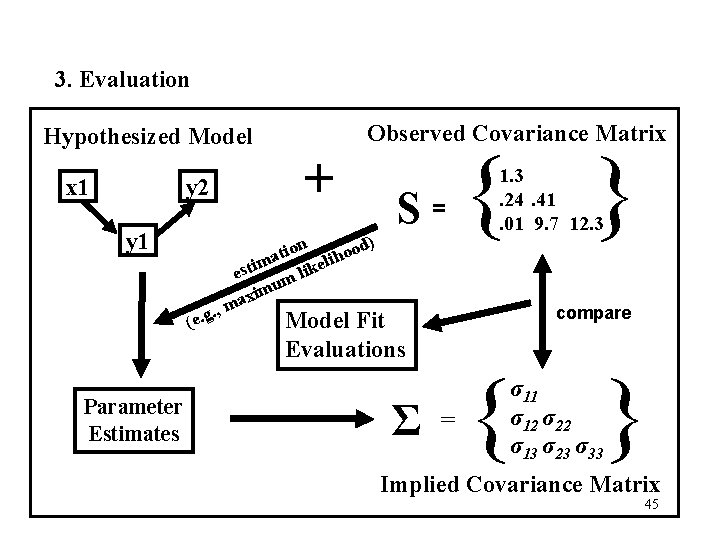
3. Evaluation Hypothesized Model x 1 y 2 y 1 + tion lihood a m e esti m lik mu i x a. , m (e. g Parameter Estimates Observed Covariance Matrix ) S= compare Model Fit Evaluations Σ { } 1. 3. 24. 41. 01 9. 7 12. 3 = { } σ11 σ12 σ22 σ13 σ23 σ33 Implied Covariance Matrix 45

Model Identification - Summary 1. For the model parameters to be estimated with unique values, they must be identified. As in linear algebra, we have a requirement that we need as many known pieces of information as we do unknown parameters. 2. Several factors can prevent identification, including: a. too many paths specified in model b. certain kinds of model specifications can make parameters unidentified c. multicollinearity d. combination of a complex model and a small sample 3. Good news is that most software checks for identification (in something called the information matrix) and lets you know which parameters are not identified. 46

Fitting Functions The most commonly used fitting function in maximum likelihood estimation of structural equation models is based on the log likelihood ratio, which compares the likelihood for a given model to the likelihood of a model with perfect fit. Note that when sample matrix and implied matrix are equal, terms 1 and 3 = 0 and terms 2 and 4 = 0. Thus, perfect model fit yields a value of FML of 0. 47

Fitting Functions (cont. ) Maximum likelihood estimators, such as FML, possess several important properties: (1) asymptotically unbiased, (2) scale invariant, and (3) best estimators. Assumptions: (1) and S matrices are positive definite (i. e. , that they do not have a singular determinant such as might arise from a negative variance estimate, an implied correlation greater than 1. 0, or from one row of a matrix being a linear function of another), and (2) data follow a multinormal distribution. 48

Assessment of Fit between Sample Covariance and Model. Implied Covariance Matrix The Χ 2 Test One of the most commonly used approaches to performing such tests (the model Χ 2 test) utilizes the fact that the maximum likelihood fitting function FML follows a X 2 (chi-square) distribution. X 2 = n-1(FML) Here, n refers to the sample size, thus X 2 is a direct function of sample size. 49

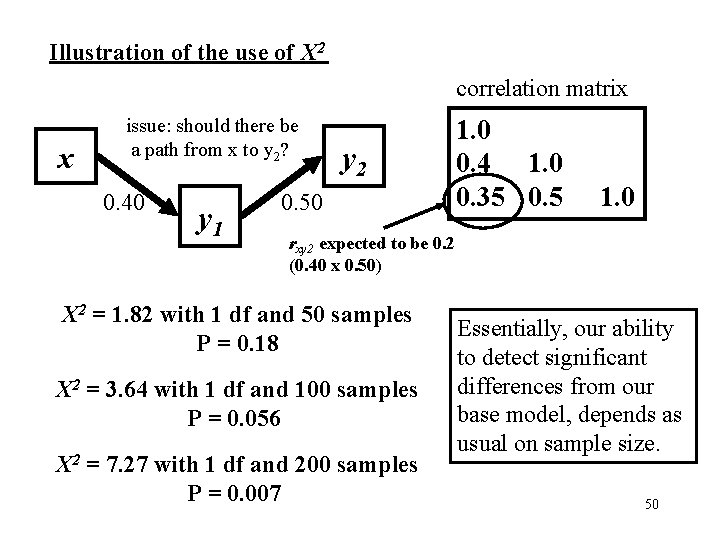
Illustration of the use of Χ 2 correlation matrix x issue: should there be a path from x to y 2? 0. 40 y 1 y 2 0. 50 1. 0 0. 4 1. 0 0. 35 0. 5 1. 0 rxy 2 expected to be 0. 2 (0. 40 x 0. 50) X 2 = 1. 82 with 1 df and 50 samples P = 0. 18 X 2 = 3. 64 with 1 df and 100 samples P = 0. 056 X 2 = 7. 27 with 1 df and 200 samples P = 0. 007 Essentially, our ability to detect significant differences from our base model, depends as usual on sample size. 50

Additional Points about Model Fit Indices: 1. The chi-square test appears to be reasonably effective at sample sizes less than 200. 2. There is no perfect answer to the model selection problem. 3. No topic in SEM has had more attention than the development of indices that can be used as guides for model selection. 4. A lot of attention is being paid to Bayesian model selection methods at the present time. 5. In SEM practice, much of the weight of evidence falls on the investigator to show that the results are repeatable (predictive of the next sample). 51

Alternatives when data extremely nonnormal Robust Methods: Satorra, A. , & Bentler, P. M. (1988). Scaling corrections for chi -square statistics in covariance structure analysis. 1988 Proceedings of the Business and Economics Statistics Section of the American Statistical Association, 308 -313. Bootstrap Methods: Bollen, K. A. , & Stine, R. A. (1993). Bootstrapping goodnessof-fit measures in structural equation models. In K. A. Bollen and J. S. Long (Eds. ) Testing structural equation models. Newbury Park, CA: Sage Publications. Alternative Distribution Specification: - Bayesian and other: 52

Diagnosing Causes of Lack of Fit (misspecification) Modification Indices: Predicted effects of model modification on model chi-square. Residuals: Most fit indices represent average of residuals between observed and predicted covariances. Therefore, individual residuals should be inspected. Correlation Matrix to be Analyzed y 1 y 2 x --------y 1 1. 00 y 2 0. 50 1. 00 x 0. 40 0. 35 1. 00 Fitted Correlation Matrix y 1 y 2 x --------y 1 1. 00 y 2 0. 50 1. 00 x 0. 40 0. 20 1. 00 residual = 0. 15 53

The topic of model selection, which focuses on how you choose among competing models, is very important. Please refer to additional tutorials for considerations of this topic. 54

While we have glossed over as many details as we could, these fundamentals will hopefully help you get started with SEM. Another gentle introduction to SEM oriented to the community ecologist is Chapter 30 in Mc. Cune, B. and J. B. Grace 2004. Analysis of Ecological Communities. MJM. (sold at cost with no profit) 55