Stats 330 Lecture 23 Department of Statistics 2012

Stats 330: Lecture 23 © Department of Statistics 2012 STATS 330 Lecture 23: Slide 1

Plan of the day In today’s lecture we continue our discussion of the multiple logistic regression model Topics covered – Models and submodels – Residuals for Multiple Logistic Regression – Diagnostics in Multiple Logistic Regression – No analogue of R 2 Reference: Coursebook, sections 5. 2. 3, 5. 2. 3 © Department of Statistics 2012 STATS 330 Lecture 23: Slide 2

Comparison of models • Suppose model 1 and model 2 are two models, with model 2 a submodel of model 1 • If Model 2 is in fact correct, then the difference in the deviances will have approximately a chi-squared distribution • df equals the difference in df of the separate models • Approximation OK for grouped and ungrouped data © Department of Statistics 2012 STATS 330 Lecture 23: Slide 3

Example: kyphosis data • Is age alone an adequate model? > age. glm<-glm(Kyphosis~Age+I(Age^2), family=binomial, data=kyphosis. df) Null deviance: 83. 234 on 80 degrees of freedom Residual deviance: 72. 739 on 78 degrees of freedom AIC: 78. 739 Full model has deviance 54. 428 on 76 df Chisq is 72. 739 - 54. 428 = 18. 311 on 78 -76=2 df > 1 -pchisq(18. 311, 2) [1] 0. 0001056372 Highly significant: need at least one of start and number © Department of Statistics 2012 STATS 330 Lecture 23: Slide 4

Anova in R Two-model form: comparing > anova(age. glm, kyphosis. glm, test=“Chi”) Analysis of Deviance Table Model 1: Model 2: Resid. 1 2 Kyphosis ~ Age + I(Age^2) + Start + Number Df Resid. Dev Df Deviance P(>|Chi|) 78 72. 739 76 54. 428 2 18. 311 0. 0001056 *** © Department of Statistics 2012 STATS 330 Lecture 23: Slide 5

Residuals • Two kinds of residuals – Pearson residuals • useful for grouped data only • similar to residuals in linear regression, actual minus fitted value – Deviance residuals • useful for grouped and ungrouped data • Measure contribution of each covariate pattern to the deviance © Department of Statistics 2012 STATS 330 Lecture 23: Slide 6

Pearson residuals Pearson residual for pattern i is Probability predicted by model Standardized to have approximately unit variance, so big if more than 2 in absolute value © Department of Statistics 2012 STATS 330 Lecture 23: Slide 7

Deviance residuals (i) • For grouped data, the deviance is © Department of Statistics 2012 STATS 330 Lecture 23: Slide 8

Deviance residuals (i) • Thus, the deviance can be written as the sum of squares of M quantities d 1, …, d. M , one for each covariate pattern • Each di is the contribution to the deviance from the ith covariate pattern • If deviance residual is big (more than about 2 in magnitude), then the covariate pattern has a big influence on the likelihood, and hence the estimates © Department of Statistics 2012 STATS 330 Lecture 23: Slide 9

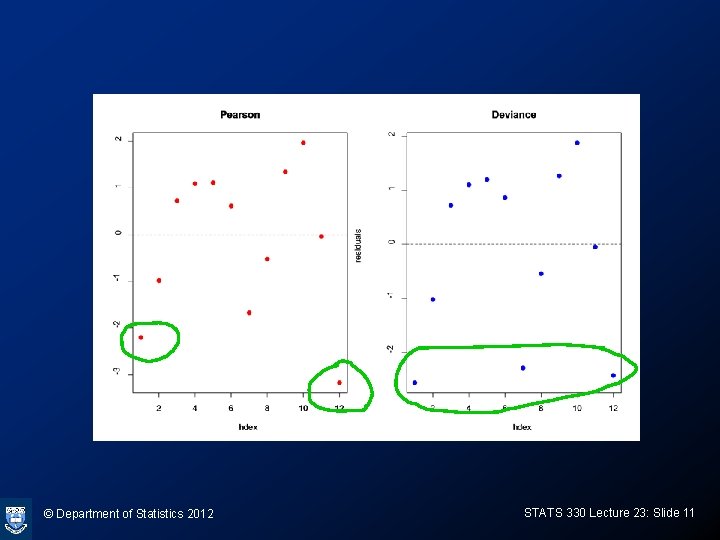
Calculating residuals > pearson. residuals<-residuals(budworm. glm, type="pearson") > deviance. residuals<-residuals(budworm. glm, type="deviance") > par(mfrow=c(1, 2)) > plot(pearson. residuals, ylab="residuals", main="Pearson") > abline(h=0, lty=2) > plot(deviance. residuals, ylab="residuals", main="Deviance") > abline(h=0, lty=2) © Department of Statistics 2012 STATS 330 Lecture 23: Slide 10

© Department of Statistics 2012 STATS 330 Lecture 23: Slide 11

Diagnostics: outlier detection • Large residuals indicate covariate patterns poorly fitted by the model • Large Pearson residuals indicate a poor match between the “maximum model probabilities” and the logistic model probabilities, for grouped data • Large deviance residuals indicate influential points • Example: budworm data © Department of Statistics 2012 STATS 330 Lecture 23: Slide 12

Diagnostics: detecting nonlinear regression functions • For a single x, plot the logits of the maximal model probabilities against x • For multiple x’s, plot Pearson residuals against fitted probabilities, against individual x’s • If the data has most ni’s equal to 1, so can’t be grouped, try gam (cf kyphosis data) © Department of Statistics 2012 STATS 330 Lecture 23: Slide 13

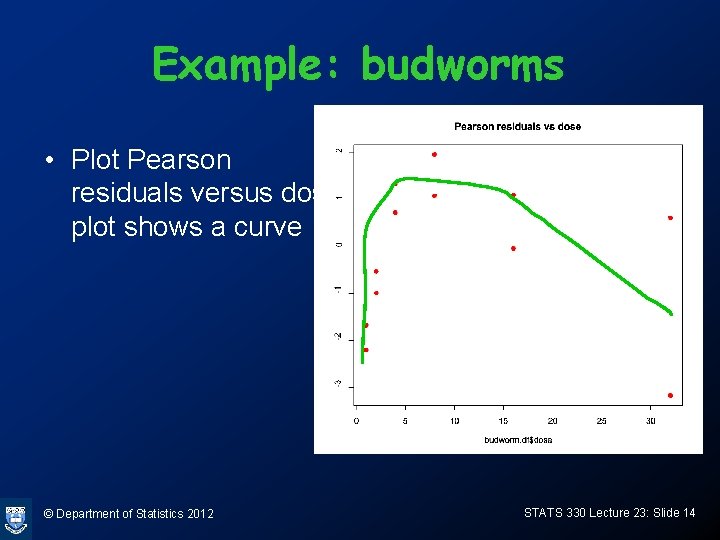
Example: budworms • Plot Pearson residuals versus dose, plot shows a curve © Department of Statistics 2012 STATS 330 Lecture 23: Slide 14

Diagnostics: influential points Will look at 3 diagnostics – Hat matrix diagonals – Cook’s distance – Leave-one-out Deviance Change © Department of Statistics 2012 STATS 330 Lecture 23: Slide 15

Example: vaso-constriction data Data from study of reflex vaso-constriction (narrowing of the blood vessels) of the skin of the fingers – Can be caused by sharp intake of breath © Department of Statistics 2012 STATS 330 Lecture 23: Slide 16

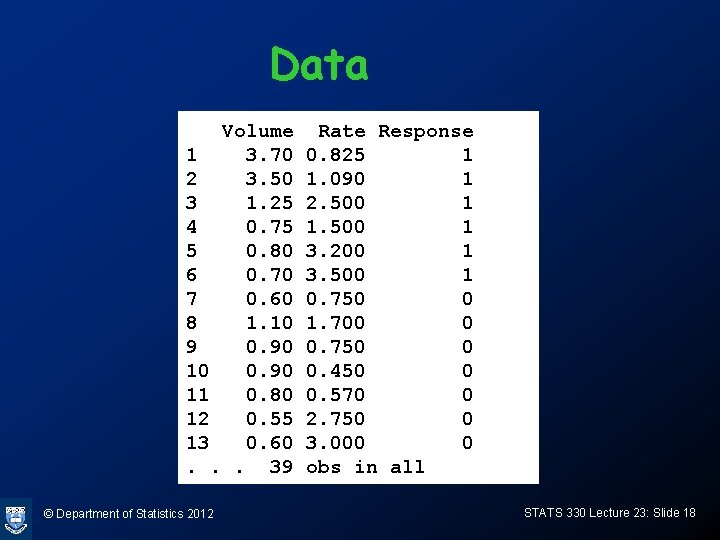
Example: vaso-constriction data Variables measured: Response = 0/1 1=vaso-constriction occurs, 0 = doesn’t occur Volume: volume of air breathed in Rate: rate of intake of breath © Department of Statistics 2012 STATS 330 Lecture 23: Slide 17

Data Volume 1 3. 70 2 3. 50 3 1. 25 4 0. 75 5 0. 80 6 0. 70 7 0. 60 8 1. 10 9 0. 90 10 0. 90 11 0. 80 12 0. 55 13 0. 60. . . 39 © Department of Statistics 2012 Rate Response 0. 825 1 1. 090 1 2. 500 1 1. 500 1 3. 200 1 3. 500 1 0. 750 0 1. 700 0 0. 750 0 0. 450 0 0. 570 0 2. 750 0 3. 000 0 obs in all STATS 330 Lecture 23: Slide 18

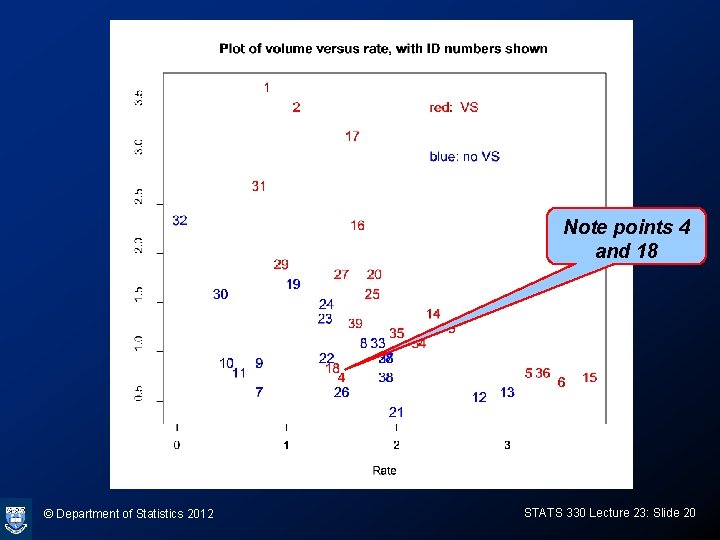
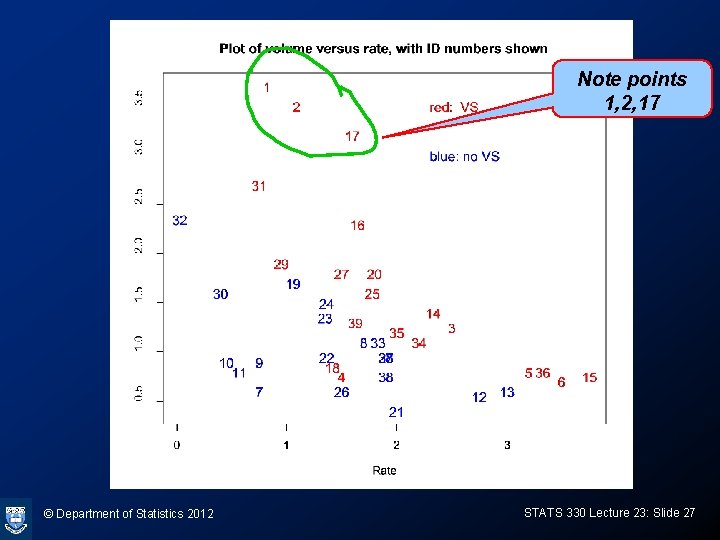
Plot of data > plot(Rate, Volume, type="n", cex=1. 2) > text(Rate, Volume, 1: 39, col=ifelse(Response==1, “red", “blue"), cex=1. 2) > text(2. 3, 3. 5, “blue: no VS", col=“blue", adj=0, cex=1. 2) > text(2. 3, 3. 0, “red: VS", col=“red", adj=0, cex=1. 2) © Department of Statistics 2012 STATS 330 Lecture 23: Slide 19

Note points 4 and 18 © Department of Statistics 2012 STATS 330 Lecture 23: Slide 20

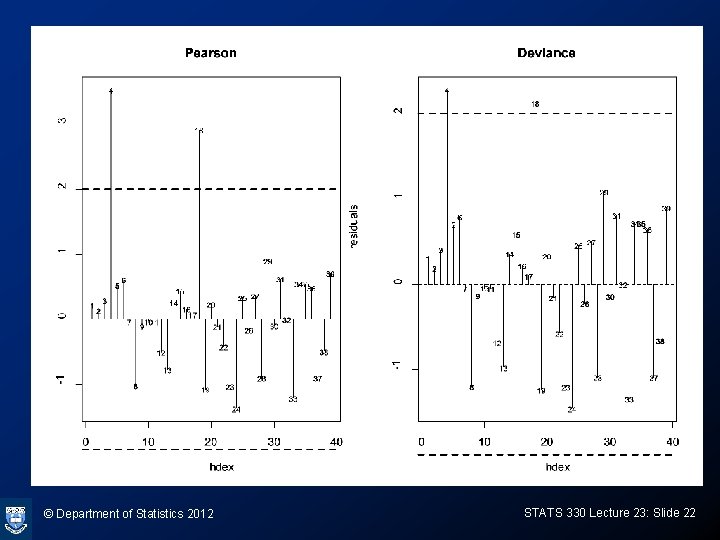
Enhanced residual plots > vaso. glm = glm(Response ~ log(Volume) + log(Rate), family=binomial, data=vaso. df) > pear. r<-residuals(vaso. glm, type="pearson") > dev. r<-residuals(vaso. glm, type="deviance") > par(mfrow=c(1, 2)) > plot(pear. r, ylab="residuals", main="Pearson", type="n") > text(pear. r, cex=0. 7) > abline(h=0, lty=2) > abline(h=2, lty=2, lwd=2) > abline(h=-2, lty=2, lwd=2) > plot(dev. r, ylab="residuals", main="Deviance", type="h") > text(dev. r, cex=0. 7) > abline(h=0, lty=2) > abline(h=2, lty=2, lwd=2) > abline(h=-2, lty=2, lwd=2) © Department of Statistics 2012 STATS 330 Lecture 23: Slide 21

© Department of Statistics 2012 STATS 330 Lecture 23: Slide 22

Diagnostics: Hat matrix diagonals • Can define hat matrix diagonals (HMD’s) pretty much as in linear models • HMD big if HMD > 3 p/M (M= no of covariate patterns) • Draw index plot of HMD’s © Department of Statistics 2012 STATS 330 Lecture 23: Slide 23

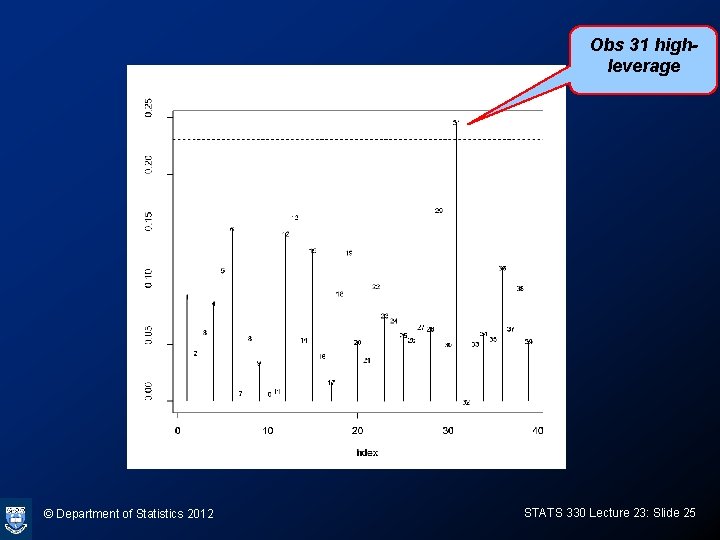
Plotting HMD’s > > HMD<-hatvalues(vaso. glm) plot(HMD, ylab="HMD's", type="h") text(HMD, cex=0. 7) abline(h=3*3/39, lty=2) © Department of Statistics 2012 STATS 330 Lecture 23: Slide 24

Obs 31 highleverage © Department of Statistics 2012 STATS 330 Lecture 23: Slide 25

Hat matrix diagonals • In ordinary regression, the hat matrix diagonals measure how “outlying” the covariates for an observation are • In logistic regression, the HMD’s measure the same thing, but are down-weighted according to the estimated probability for the observation. The weights gets small if the probability is close to 0 or 1. • In the vaso-constriction data, points 1, 2, 17 had very small weights, since the probabilities are close to 1 for these points. © Department of Statistics 2012 STATS 330 Lecture 23: Slide 26

Note points 1, 2, 17 © Department of Statistics 2012 STATS 330 Lecture 23: Slide 27

Diagnostics: Cooks distance • Can define an analogue of Cook’s distance for each point CD = (Pearson resid )2 x HMD/(p*(1 -HMD)2) p = number of coeficients • CD big if more than about 10% quantile of the chisquared distribution on k+1 df, divided by k+1 • Calculate with qchisq(0. 1, k+1)/(k+1) • But not that reliable as a measure © Department of Statistics 2012 STATS 330 Lecture 23: Slide 28

Cooks D: calculating and plotting p<-3 CD<-cooks. distance(vaso. glm) plot(CD, ylab="Cook's D", type="h", main="index plot of Cook's distances") text(CD, cex=0. 7) bigcook<-qchisq(0. 1, p)/p abline(h=bigcook, lty=2) © Department of Statistics 2012 STATS 330 Lecture 23: Slide 29

Points 4 and 18 influential © Department of Statistics 2012 STATS 330 Lecture 23: Slide 30

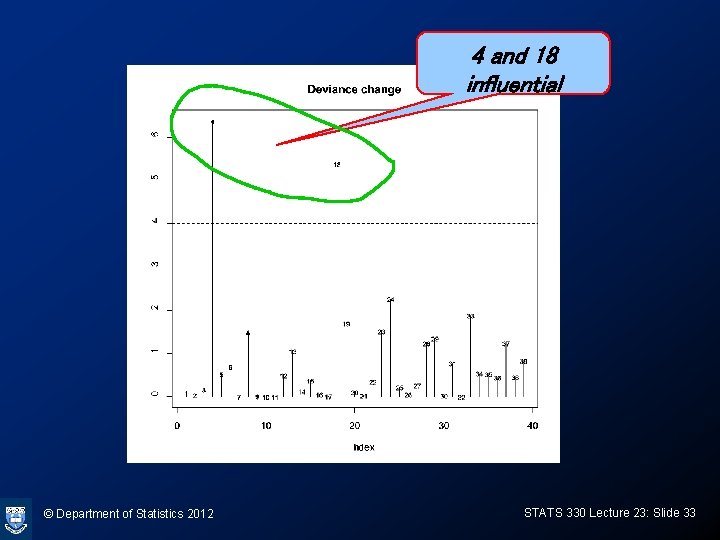
Diagnostics: leave-one-out deviance change • If the ith covariate pattern is left out, the change in the deviance is approximately (Dev. Res) 2 + (Pearson. Res)2 HMD/(1 -HMD) Big if more than about 4 © Department of Statistics 2012 STATS 330 Lecture 23: Slide 31

Deviance change: calculating and plotting > dev. r<-residuals(vaso. glm, type="deviance") > Dev. change<-dev. r^2 + pear. r^2*HMD/(1 -HMD) > plot(Dev. change, ylab="Deviance change", type="h") > text(Dev. change, cex=0. 7) > bigdev<-4 > abline(h=bigdev, lty=2) © Department of Statistics 2012 STATS 330 Lecture 23: Slide 32

4 and 18 influential © Department of Statistics 2012 STATS 330 Lecture 23: Slide 33

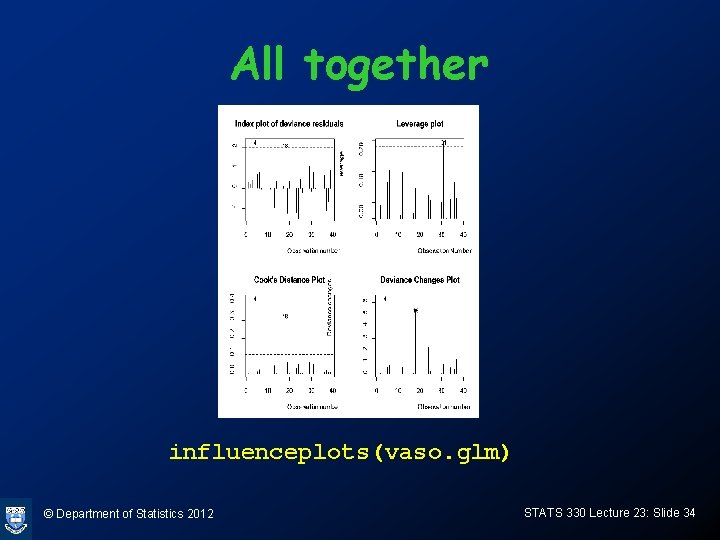
All together influenceplots(vaso. glm) © Department of Statistics 2012 STATS 330 Lecture 23: Slide 34

Should we delete points? • How influential are the 3 points? • Can delete each in turn and examine changes in coefficients, predicted probabilities • First, coefficients: Deleting: None 31 4 18 All 3 (Intercept) -2. 875 -3. 041 -5. 206 -4. 758 -24. 348 log(Volume) 5. 179 4. 966 8. 468 7. 671 39. 142 log(Rate) 4. 562 4. 765 7. 455 6. 880 31. 642 © Department of Statistics 2012 STATS 330 Lecture 23: Slide 35

Should we delete points (2)? • Next, fitted probabilities: Fitted at None 31 point 31 0. 722 0. 627 point 4 0. 075 0. 073 point 18 0. 106 0. 100 delete points 4 18 4 and 18 0. 743 0. 707 0. 996 0. 010 0. 015 0. 000 0. 018 0. 026 0. 000 All 3 0. 996 0. 000 • Conclusion: points 4 and 18 have a big effect. © Department of Statistics 2012 STATS 330 Lecture 23: Slide 36

Should we delete points (3)? • Should we delete? • They could be genuine – no real evidence they are wrong • If we delete them, we increase the regression coefficients, make fitted probabilities more extreme • Overstate the predictive ability of the model © Department of Statistics 2012 STATS 330 Lecture 23: Slide 37

Residuals for ungrouped data • If all cases have distinct covariate patterns, then the residuals lie along two curves (corresponding to success and failure) and have little or no diagnostic value. • Thus, there is a pattern even if everything is OK. © Department of Statistics 2012 STATS 330 Lecture 23: Slide 38

Formulas • Pearson residuals: for ungrouped data, residual for i th case is © Department of Statistics 2012 STATS 330 Lecture 23: Slide 39

Formulas (cont) • Deviance residuals: for ungrouped data, residual for i th case is © Department of Statistics 2012 STATS 330 Lecture 23: Slide 40

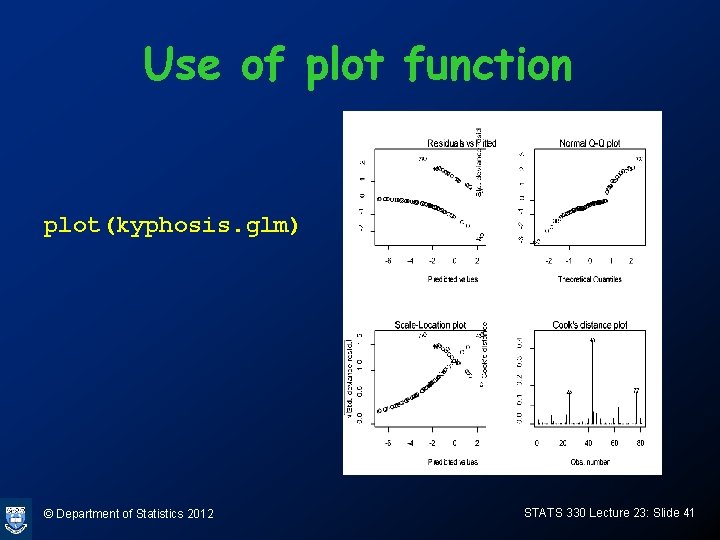
Use of plot function plot(kyphosis. glm) © Department of Statistics 2012 STATS 330 Lecture 23: Slide 41

Analogue of R 2? • There is no satisfactory analogue of R 2 for logistic regression. • For the “small m big n” situation we can use the residual deviance, since we can obtain an approximate p-value. • For other situations we can use the Hosmer –Lemeshow statistic (next slide) © Department of Statistics 2012 STATS 330 Lecture 23: Slide 42

Hosmer-Lemeshow statistic • How can we judge goodness of fit for ungrouped data? • Can use the Hosmer-Lemeshow statistic, which groups the data into cases having similar fitted probabilities – Sort the cases in increasing order of fitted probabilities – Divide into 10 (almost) equal groups – Do a chi-square test to see if the number of successes in each group matches the estimated probability © Department of Statistics 2012 STATS 330 Lecture 23: Slide 43

Kyphosis data Divide probs into 10 classes : lowest 10%, next 10%. . . Class 1 Class 2 Class 3 Class 4 Class 5 Observed 0’s 9 8 8 7 8 Observed 1’s 0 0 0 1 0 Total obs 9 8 8 Expected 1’s 0. 022 0. 082 0. 199 0. 443 0. 776 Class 7 Class 8 Class 9 Class 10 Observed 0’s 8 5 5 3 3 Observed 1’s 0 3 3 5 5 Total obs 8 8 8 Expected 1’s 1. 023 1. 639 2. 496 3. 991 6. 328 Note: Expected = Total. obs x average prob © Department of Statistics 2012 STATS 330 Lecture 23: Slide 44

In R, using the kyphosis data Result of fitting model > HLstat(kyphosis. glm) Value of HL statistic = P-value = 0. 592 6. 498 A p-value of less than 0. 05 indicates problems. No problem indicated for the kyphosis data – logistic appears to fit OK. The function HLstat is in the “ 330 functions” © Department of Statistics 2012 STATS 330 Lecture 23: Slide 45