Statistic multivariat prezentat de Valentin Clocotici Analiza factorial

Statistică multivariată prezentată de Valentin Clocotici

Analiza factorială (1) Cursul nr. 10 05 -Mar-21 2

Analiza datelor – metode factoriale • Prin analiza datelor se înţeleg de obicei metodele statisticii descriptive multidimensionale. • Metodele se grupează în: – metode factoriale, – metode de clasificare. • Metodele factoriale îşi au originea în tehnicile de analiză factorială propuse şi dezvoltate de psihologi (la începutul sec. XX). Ele utilizează metode din algebra liniară şi produc reprezentări grafice care ajută la înţelegerea structurii datelor. • Metodele de clasificare sunt mai recente, de natură algoritmică, şi produc clase care permit gruparea obiectelor studiate. • Cele două familii de metode sunt, mai degrabă, complementare, decât concurente, producând viziuni care întregesc înţelegerea domeniului studiat. 05 -Mar-21 3

Analiza factorială Scopul: Înţelegerea cauzelor • Analiza factorială, spre deosebire de alte metode statistice, nu studiază relaţia dintre variabilele dependente şi cele independente observate. • Analiza factorială îşi propune să studieze pattern-ul relaţiilor dintre variabilele observate (considerate variabile dependente), cu scopul de a descoperi ceva din natura variabilelor independente care afectează variabilele dependente, chiar dacă variabilele independente nu au fost observate direct. • Astfel, răspunsurile obţinute prin analiza factorială sunt mai mult ipotetice, tentative de descoperire a dependenţelor. • Variabilele independente obţinute sunt numite factori. 05 -Mar-21 4

Analiza factorială • O analiză factorială trebuie să ofere răspunsuri la patru întrebări majore: – Câţi factori diferiţi sunt necesari pentru a explica pattern ul relaţiilor? – Care este natura acestor factori? – Cât de bine sunt explicate datele observate de factorii reţinuţi? – Cât de multă varianţă pur aleatorie sau fixă include fiecare variabilă observată? • Utilizare directă – identificarea grupurilor de variabile intercorelate, – reducerea numărului de variabile. • Utilizare indirectă: – o metodă de transformare a datelor. Datele transformate au proprietăţi pe care datele iniţiale nu le aveau. Datele pot fi transformate eficient înainte de a încerca o clasificare. 05 -Mar-21 5

Analiza factorială Reducerea dimensiunii • Presupunem că într-un studiu observaţional s-au înregistrat valori pentru un număr mare, p, de variabile (de exemplu, întrun studiu sociologic s-au înregistrat răspunsurile la 100 de întrebări; există deci 100 de variabile urmărite în studiu şi este foarte dificil să se înţeleagă relaţiile dintre aceste variabile). • Pentru determinarea structurii (pattern-ului) acestor variabile, ca şi pentru structura proprie observaţiilor efectuate, este de dorit să aibă loc o reducere a dimensiunilor (mai puţine variabile, mai puţine observaţii). • Dacă acest proces se efectuează în mod mecanic, prin renunţarea la unele variabile, este normal să aibă loc o simplificare exagerată, cu o pierdere de informaţii esenţiale. • Din acest motiv este de preferat ca reducerea dimensiunii să aibă loc în urma unei analize globale. 05 -Mar-21 6

Analiza factorială • Metodele factoriale pot fi privite ca tehnici de reducere a dimensiunii problemei studiate, considerându-se însă întregul set de date observate. • Ideea este aceea de a crea un număr mai mic de noi variabile care să explice cât mai mult din varianţa variabilelor iniţiale, pornind de la argumentul intuitiv că dacă variabilele iniţiale sunt puternic corelate, atunci ele exprimă “cam acelaşi lucru”, deci se poate reduce numărul lor. • Mai mult, dacă anumite variabile sunt puternic corelate, se poate ca acest fapt să se datoreze unei variabile ascunse care le influenţează puternic; această nouă variabilă poate înlocui grupul iniţial. 05 -Mar-21 7

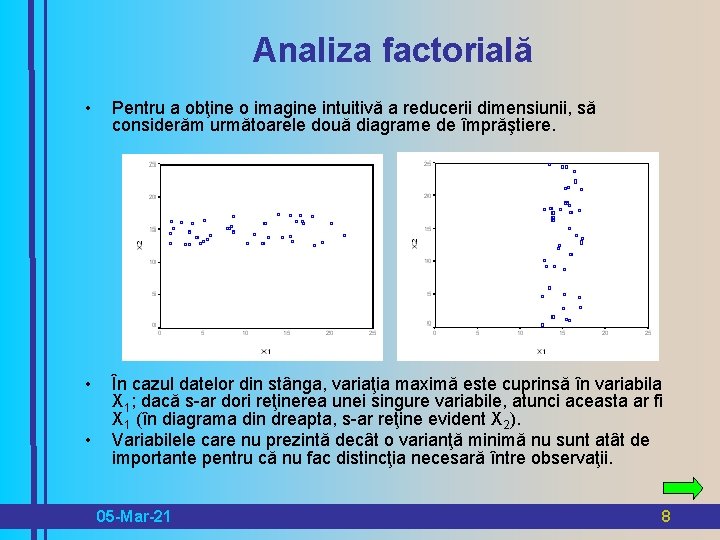
Analiza factorială • Pentru a obţine o imagine intuitivă a reducerii dimensiunii, să considerăm următoarele două diagrame de împrăştiere. • În cazul datelor din stânga, variaţia maximă este cuprinsă în variabila X 1; dacă s-ar dori reţinerea unei singure variabile, atunci aceasta ar fi X 1 (în diagrama din dreapta, s-ar reţine evident X 2). Variabilele care nu prezintă decât o varianţă minimă nu sunt atât de importante pentru că nu fac distincţia necesară între observaţii. • 05 -Mar-21 8

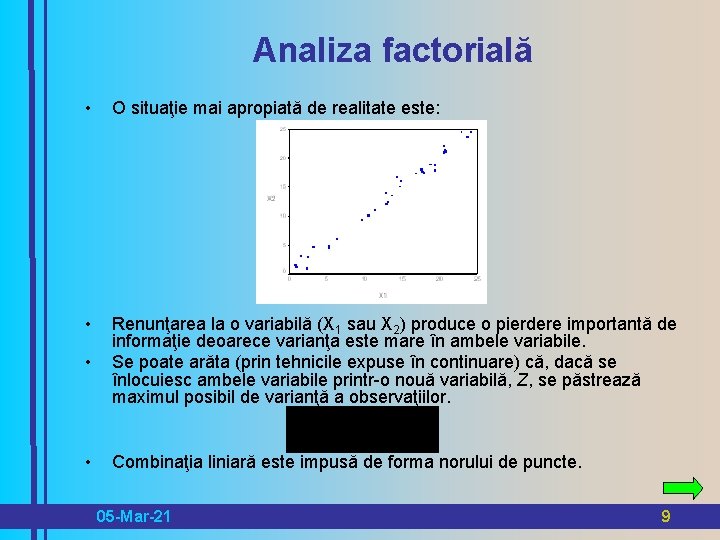
Analiza factorială • O situaţie mai apropiată de realitate este: • • Renunţarea la o variabilă (X 1 sau X 2) produce o pierdere importantă de informaţie deoarece varianţa este mare în ambele variabile. Se poate arăta (prin tehnicile expuse în continuare) că, dacă se înlocuiesc ambele variabile printr-o nouă variabilă, Z, se păstrează maximul posibil de varianţă a observaţiilor. • Combinaţia liniară este impusă de forma norului de puncte. 05 -Mar-21 9

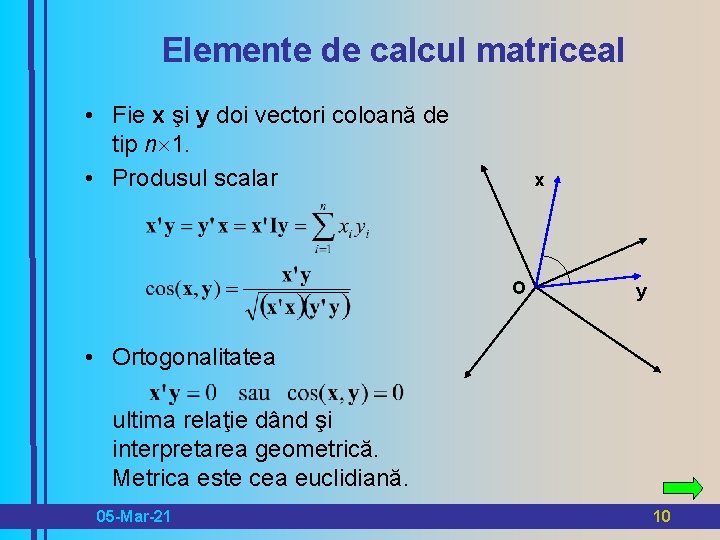
Elemente de calcul matriceal • Fie x şi y doi vectori coloană de tip n 1. • Produsul scalar x O y • Ortogonalitatea ultima relaţie dând şi interpretarea geometrică. Metrica este cea euclidiană. 05 -Mar-21 10

Elemente de calcul matriceal • Formă pătratică: este funcţia reală de argumente xi unde A este o matrice simetrică de tip (n, n) iar x este un vector coloană de tip (n, 1) • O formă pătratică se zice – Pozitiv definită dacă x’Ax > 0 pentru orice x 0 – Semipozitiv definită dacă x’Ax 0 pentru orice x (poate exista x 0 încât x’Ax = 0). 05 -Mar-21 11

Elemente de calcul matriceal • Exemple: x’Ix este o formă pătratică pozitiv definită; X’X şi XX’ sunt matrice simetrice semipozitiv definite (asociate cu forme pătratice semipozitiv definite). • Combinaţie liniară: fie x 1, x 2, …, xp vectori coloană de tip (n, 1) şi c 1, c 2, …, cp constante reale. Vectorul combinaţie liniară este c 1 x 1 + c 2 x 2 + … + cpxp • Independenţă liniară: vectorii x 1, x 2, …, xp sunt liniar independenţi (sau independenţi) dacă c 1 x 1 + c 2 x 2 + … + cpxp = 0 implică c 1=c 2=…=cp=0 05 -Mar-21 12

Elemente de calcul matriceal • Fie A o matrice pătratică de tip (p, p), un scalar şi x un vector nenul de tip (p, 1), astfel încât Ax = x atunci A(sx) = (sx) pentru orice scalar s (deci x este determinat până la un factor) şi, prin urmare, putem impune ca x să fie de lungime 1 (x’x=1). Deci (A – I)x = 0 cu x’x = 1 • Se ajunge la ecuaţia caracteristică det (A – I) = 0 de unde se poate determina . • Ca definiţii, se numeşte valoare proprie a lui A iar x se numeste vector propriu a lui A corespunzător valorii proprii . 05 -Mar-21 13

Elemente de calcul matriceal Proprietăţi – Suma valorilor proprii este egală cu urma matricei A (suma termenilor de pe diagonala principală). tr A = aii – Produsul valorilor proprii este egal cu determinantul matricei A. – Dacă A este o matrice pătrată şi P este nesingulară, atunci A şi PAP-1 au aceleaşi valori proprii. – Aceeaşi proprietate are loc şi dacă P este ortogonală (P’P = I, deci P’ = P-1). 05 -Mar-21 14

Elemente de calcul matriceal Proprietăţi – Dacă A este simetrică, atunci toate valorile proprii sunt reale şi orice doi vectori proprii (corespunzând la valorii proprii distincte) sunt ortogonali. – Dacă A este simetrică, numărul valorilor proprii nenule este egal cu rangul matricei. – Dacă A este simetrică şi pozitiv definită, atunci toate valorile proprii sunt pozitive. – Dacă A este simetrică şi semipozitiv definită, atunci toate valorile proprii sunt nenegative. 05 -Mar-21 15

Analiza factorială – metoda generală • Întrebare: – Este posibil să reconstituim cele np valori xij ale unui tablou Xn p pornind de la un număr mai mic de date? • Răspunsul poate fi afirmativ: dacă X = u 1 v 1’, unde un 1 şi vp 1, atunci se poate reconstitui X din cele n+p valori ale lui u 1 şi v 1. Se spune că X este de rang 1. • În practică este foarte improbabilă o asemenea descompunere şi se va căuta o ajustare de rang q, de forma unde E este o matrice reziduală, cu termeni suficient de mici astfel încât cele np valori din X să fie reconstituite suficient de bine din cele q(n+p) valori ale vectorilor u şi v , =1, …, q. 05 -Mar-21 16

Analiza factorială – metoda generală • Problema se va rezolva cu ajutorul reprezentărilor geometrice. • Tabloul X poate fi privit drept mulţimea coordonatelor punct în R n – a n puncte în spaţiul cu p dimensiuni, R p (fiecare linie a tabloului este un punct în acest spaţiu), sau – ca p puncte în spaţiul cu n dimensiuni, R n (fiecare coloană a tabloului este un punct în acest spaţiu). • Ambele spaţii se consideră dotate cu metrica euclidiană uzuală. 05 -Mar-21 punct în R p 17

Analiza factorială – metoda generală Ajustarea printr-un subspaţiu vectorial din R p • Ideea este aceea determina un subspaţiu vectorial de dimensiune q < p în care să fie conţinută X (matricea X este gândită ca mulţimea a n vectori – coloanele matricei). • În acest caz, cele n puncte din X pot fi reconstituite plecând de la – coordonatele pe noile q axe, adică nq valori, – componentele noilor axe în spaţiul iniţial, adică pq valori. • Se utilizează astfel nq + pq valori. – Dacă, de exemplu, n = 1000, p = 100 şi q = 4, se vor reconstitui cele np = 105 valori din numai 4400 de valori. 05 -Mar-21 18

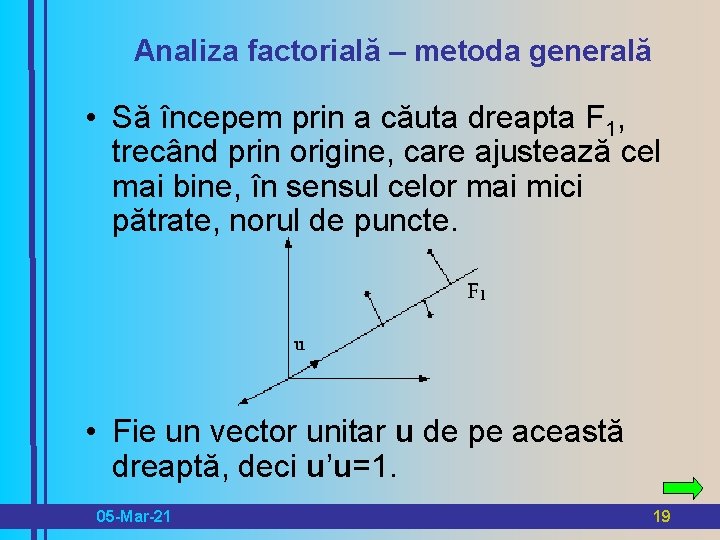
Analiza factorială – metoda generală • Să începem prin a căuta dreapta F 1, trecând prin origine, care ajustează cel mai bine, în sensul celor mai mici pătrate, norul de puncte. • Fie un vector unitar u de pe această dreaptă, deci u’u=1. 05 -Mar-21 19

Analiza factorială • Rezultă că fiecare linie din Xu este produsul scalar al punctului respectiv cu u şi deci lungimea proiecţiei punctului pe F 1. • Prin urmare, minimizarea sumei distanţelor la F 1 (criteriul celor mai mici pătrate) revine la maximizarea sumei proiecţiilor. • Deci determinarea lui F 1 conduce la maximizarea sumei pătratelor acestor proiecţii, adică se caută u care maximizează (Xu)’(Xu)=u’X’Xu, cu restricţia u’u=1. 05 -Mar-21 20

Analiza factorială • Prin metoda multiplicatorului Lagrange, se consideră L = u’X’Xu - ( u’u-1) şi anularea derivatelor parţiale în raport cu u conduce la 2 X’Xu-2 u=0, de unde X’Xu = u ceea ce arată că u este un vector propriu al matricei X’X. Atunci, u’X’Xu = u’u şi, din restricţia impusă, rezultă u’X’Xu = , adică maximul căutat este egal cu o valoare proprie a lui X’X. • Prin urmare, u este acel vector propriu u 1 care corespunde celei mari valori proprii 1. 05 -Mar-21 21

Analiza factorială • În general, se arată că o bază ortonormată a subspaţiului vectorial cu q dimensiuni, care ajustează norul de puncte în sensul celor mai mici pătrate, este constituită din cei q vectori proprii care corespund celor mai mari q valori proprii ale matricei simetrice X’X. • Notăm cu u 1, u 2, …, uq vectorii proprii şi 1, 2, …, q valorile proprii corespunzătoare. • De remarcat că matricea X’X este simetrică şi semipozitiv definită, deci toate valorile proprii sunt reale nenegative, iar vectorii proprii sunt ortogonali. 05 -Mar-21 22

Analiza factorială Ajustarea printr‑un subspaţiu vectorial din R n • În R n, coloanele matricei Xn p definesc un nor de p puncte. • Raţionând analog (pe matricea X’) se ajunge la: – cel mai bun subspaţiu cu q dimensiuni este generat de vectorii proprii v 1, v 2, …, vq care corespund la valorile proprii (descrescătoare) 1, 2, …, q ale matricei XX’. 05 -Mar-21 23

Analiza factorială Relaţia dintre cele două subspaţii din R p şi R n • Din definiţia vectorului propriu v , avem XX’v = v de unde, prin înmulţire la stânga cu X’, X’XX’ v = X’v adică (X’X)(X’ v ) = (X’v ) • Deci fiecărui vector propriu v a lui XX’ îi corespunde un vector propriu egal cu X’v a matricei X’X iar este valoare proprie pentru X’X. Adică { ) { } • Analog se demonstrează şi incluziunea inversă. 05 -Mar-21 24

Analiza factorială Relaţia dintre subspaţiile din R p şi R n • Se arată astfel identitatea celor două mulţimi de valori proprii, = 1, …, r, unde r este rang(X), r min(p, n). • Intre vectorii proprii există relaţiile (cu observaţia că egalitatea are loc până la un factor) ua = k X’v va = k’ X’u unde k şi k’ sunt constante necunoscute. • Din u’ u = v’ v = 1 rezultă • Dar v’ XX’v = = de unde 05 -Mar-21 25

Analiza factorială • Intre vectorii proprii din cele două spaţii există astfel relaţiile • Axa F , care poartă vectorul unitar u , este numită a -a axă factorială din R p. Analog pentru G în R n. • Coordonatele punctelor pe axa din R p (şi respectiv din R n) sunt, prin construcţie, componentele lui Xu (respectiv X’v ). • Relaţiile precedente arată proporţionalitatea care există între coordonatele punctelor pe o axă dintr-un spaţiu şi componentele unitare (cosinuşii directori) ai axei în celălalt spaţiu. 05 -Mar-21 26

Analiza factorială 05 -Mar-21 27

Analiza factorială • O reconstituire aproximativă X* este obţinută prin limitarea la primele q axe factoriale (reamintim că valorile proprii au fost luate în ordine descrescătoare, deci q+1, …, p sunt valorile cele mai mici): • Calitatea globală a reconstituirii poate fi măsurată prin cantitatea numită rata de inerţie (măsoară partea din varianţa norului de puncte imputabilă subspaţiului cu q dimensiuni). 05 -Mar-21 28

Analiza factorială • Fiecare valoare proprie măsoară suma pătratelor distanţelor la origine ale proiecţiilor pe axa factorială respectivă. Prin urmare, reconstituirea va fi cu atât mai bună cu cât suma valorilor proprii reţinute va constitui o parte notabilă a sumei tuturor valorilor proprii. • Se poate verifica şi egalitatea care oferă un suport intuitiv faptului că t reflectă calitatea globală a reconstituirii. 05 -Mar-21 29

Analiza factorială Analize particulare • Atunci când nu este vorba strict de o aproximare numerică şi ne încadrăm în analiza statistică, dispunem de informaţii suplimentare asupra naturii datelor. • Considerarea acestor informaţii conduce la transformări prealabile ale datelor iniţiale, astfel încât aplicarea metodei generale la datele transformate permite interpretări mai adecvate structurii datelor. • Se obţin astfel analize factoriale particulare, cele mai importante sunt enumerate în continuare: – – Analiza în componente principale, Analiza în componente principale normate, Analiza rangurilor, Analiza corespondenţelor. 05 -Mar-21 30

Analiza factorială • Ideea de bază care stă la baza tuturor acestor analize este aceea că – un tabel de valori poate produce (prin liniile, respectiv coloanele sale) reprezentări sub forma norilor de puncte în două spaţii. – Ajustările punctelor din cele două spaţii sunt legate prin relaţii simple, interpretabile. • De regulă, analizele vor produce diagrame care evidenţiază structura norilor de puncte. • Metodele pot fi gândite şi ca metode algebrice care permit alegerea sistemului de referinţă şi a punctului de vedere, astfel încât imaginea norului de puncte să fie cât mai clară, mai relevantă pentru structurarea punctelor. 05 -Mar-21 31

Analiza factorială • In imaginile prezentate se încearcă vizualizări ale unei aceleiaşi structuri de puncte, pentru a ilustra, dacă mai este necesar, dependenţa dintre înţelegerea structurii şi punctul de vedere (sau transformarea prealabilă). Din păcate trebuie să ne limităm doar la cazul 3 D. a) 05 -Mar-21 b) c) 32

Analiza factorială Analiza în componente principale • Iniţiată de Pearson (1901) şi dezvoltată de Hotelling (1933). • Tabloul de plecare R este oarecare: rij semnifică, în mod uzual, a i-a observaţie a variabilei j. • Variabilele pot fi eterogene în privinţa mediilor (de ex. unităţi de măsură diferite, ordine de mărime diferite etc. ). • Efectul eterogenităţii se anulează prin transformarea unde este media variabilei j. • Analiza generală se va aplica tabloului X astfel obţinut (X este matricea de covarianţă a variabilelor). 05 -Mar-21 33

Analiza factorială Analiza în componente principale normate • Dacă variabilele sunt eterogene în medie şi în dispersie, se vor norma valorile prin unde sj este abaterea standard pentru variabila j. • Analiza generală se va aplica tabloului X, cu observaţia că că matricea X’X implicată în calcule este tocmai matricea de corelaţie a variabilelor. 05 -Mar-21 34

Analiza factorială Analiza rangurilor • Matricea de observaţii R este înlocuită în prealabil prin matricea rangurilor, P, caz impus în situaţia în care variabilele sunt ordinale (contează ordinea valorilor şi nu se poate defini distanţa dintre valori). • Cu alte cuvinte, fiecare valoare rij este înlocuită cu pij = (rangul valorii rij în cele n valori ale variabilei j). • În acest caz toate variabilele au aceeaşi medie, m=(n + 1)/2 şi aceeaşi dispersie, s 2=(n 2 -1)/12. • Analiza în componente principale normate aplicată tabloului P este numită analiza rangurilor. • Matricea X’X este, în această analiză, matricea de corelaţie a rangurilor (Spearman). 05 -Mar-21 35

Analiza factorială Analiza corespondenţelor • Se aplică atunci când tabloul iniţial este un tablou de frecvenţe (fij), sau un tablou de numere pozitive. • Datele iniţiale se transformă prin unde • Analiza generală se aplică tabloului X astfel obţinut. • Este de remarcat rolul simetric jucat în acest caz de indicii i şi j, ceea ce este perfect pentru analizarea tabelelor de frecvenţe încrucişate. 05 -Mar-21 36

Analiza în componente principale (normate) ACP/ACPN • Numele metodei provine din aceea că factorii (obţinuţi prin analiza generală) sunt numiţi şi componente principale. • Deşi pentru identificarea factorilor se aplică metoda generală asupra matricei de covarianţă (corelaţie) a variabilelor implicate, în continuare se prezintă şi o metodă alternativă, care poate oferi o viziune mai intuitivă asupra calculelor efectuate. • Se doreşte reducerea numărului de variabile dar cu păstrarea a cât mai mult (în limita posibilităţilor) din varianţa datelor iniţiale. • Pentru aceasta se introduce o nouă variabilă, Z, ca o combinaţie liniară a variabilelor iniţiale: unde a 1, …, ap sunt ponderi asociate variabilelor iniţiale. • De notat că ecuaţia precedentă este doar aparent similară unei ecuaţii de regresie, deoarece nu se cunosc valori observate pentru variabila Z, nu există termen liber şi nici erori (reziduuri). 05 -Mar-21 37

ACP/ACPN • Scopul analizei în componente principale este acela determina acele ponderi ai care maximizează varianţa variabilei Z. • Cum varianţa poate tinde la infinit pentru valori ale ponderilor convenabil alese, metoda determină doar ponderile supuse restricţiei că vectorul a este normalizat, adică • O dată calculate ponderile a, variabila Z este numită prima componentă principală. 05 -Mar-21 38

ACP/ACPN • Fie C matricea de covarianţă (ACP) sau de corelaţie (ACPN) a variabilelor X. Varianţa lui Z este atunci a’Ca. • Se doreşte maximizarea varianţei lui Z cu restricţia a’a = 1. • Prin metoda multiplicatorilor lui Lagrange se va căuta maximul funcţiei F(a) = a’Ca - (a’a – 1) • De unde rezultă, ca în metoda generală, că a este vector propriu al matricei C, corespunzător valorii proprii . • Cum Var(Z) = , rezultă că a corespunde celei mari valori proprii . 05 -Mar-21 39

ACP/ACPN • A doua componentă principală este definită drept combinaţia liniară a variabilelor X cu următoarea cea mai mare varianţă: Z 2 = a 12 X 1 + a 22 X 2 + … + ap 2 Xp • Se ajunge astfel la a doua valoare proprie ca mărime etc. De remarcat că aij reprezintă ponderea variabilei i în componenta principală cu numărul j. • Se arată, în continuare, că factorii obţinuţi (componentele principale) sunt necorelate între ele. • Astfel, din exprimarea matriceală z = Ax a componentelor principale şi din faptul că matricea vectorilor proprii este ortogonală, A’A = I, rezultă A’z = A’Ax = Ix = x. 05 -Mar-21 40

ACP/ACPN • Se observă astfel că şi variabilele iniţiale pot fi exprimate drept combinaţii liniare ale componentelor principale. • Din relaţia x = A’z rezultă că matricea C de covarianţă a lui x este C = A’Czz. A. unde Czz este covarianţa componentelor principale. • Utilizând rezultatul, cunoscut din algebra liniară, că C = A’ A, unde este matricea diagonală a valorilor proprii, rezultă că Czz este o matrice diagonală, adică toate componentele principale sunt necorelate între ele. • Se observă astfel că prin trecerea la componentele principale se elimină redundanţa din date. 05 -Mar-21 41

ACP/ACPN Analiza în R p • Cele n puncte ale acestui spaţiu sunt indivizi (observaţii) şi se doreşte o reprezentare a apropierilor dintre aceste puncte într-un spaţiu de dimensiune mai mică. • Prin transformările prealabile are loc o translaţie a norului de puncte într-un reper având ca origine centrul de greutate al norului. • In ACPN se modifică şi scala pe fiecare axă. 05 -Mar-21 42

ACP/ACPN Analiza în R n • Cele p puncte sunt aici variabilele, transformările prealabile au însă o interpretare diferită: – transformarea din ACP este o proiecţie paralelă cu prima bisectoare – transformarea din ACPN este o deformare a norului de puncte care aduce fiecare punct variabilă la distanţa 1 de origine (pe sfera unitate). • Distanţa dintre două puncte este d 2(j, j’) = 2(1 – cor(j, j’)), adică proximităţile dintre puncte se pot interpreta în termenii corelaţiilor dintre variabile. • Coordonatele punctelor variabile pe o axă sunt coeficienţii de corelaţie dintre variabile şi factorul respectiv (considerat ca o nouă variabilă). • Prin urmare se poate interpreta un factor (axă) drept o combinaţie a variabilelor cele mai corelate cu el. 05 -Mar-21 43