Two New Classes of Hamiltonian Graphs Valentin Polishchuk

Two New Classes of Hamiltonian Graphs Valentin Polishchuk Helsinki Institute for Information Technology, University of Helsinki Joint work with Esther Arkin and Joseph Mitchell Applied Math and Statistics, Stony Brook University

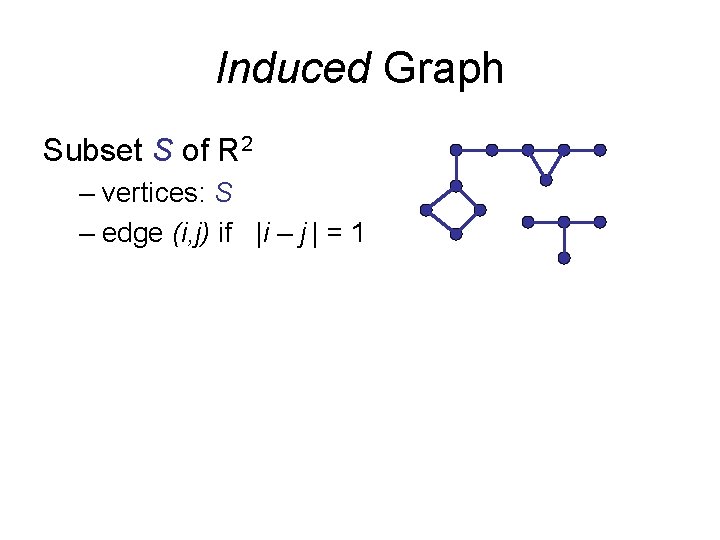
Induced Graph Subset S of R 2 – vertices: S – edge (i, j) if |i – j | = 1

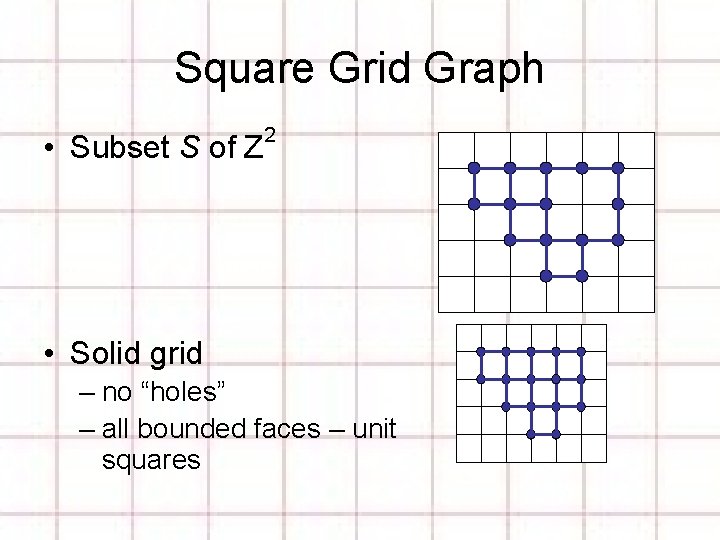
Square Grid Graph • Subset S of Z 2 • Solid grid – no “holes” – all bounded faces – unit squares

Hamiltonicity of Square Grids • NP-complete in general [Itai, Papadimitriou, and Szwarcfiter ’ 82] • Solid grids – polynomial [Umans and Lenhart ’ 96]

Tilings • Square grid – unit squares

Tilings • Square grid – unit squares • Triangular grid – unit equilateral triangles

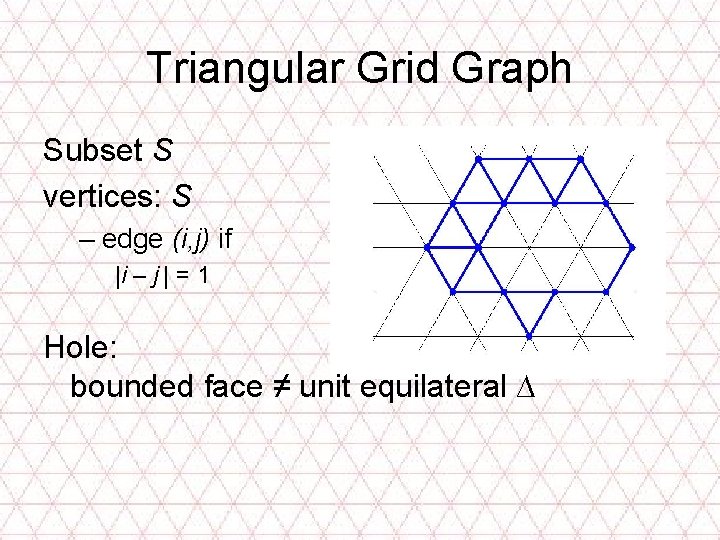
Triangular Grid Graph Subset S vertices: S – edge (i, j) if |i – j | = 1 Hole: bounded face ≠ unit equilateral ∆

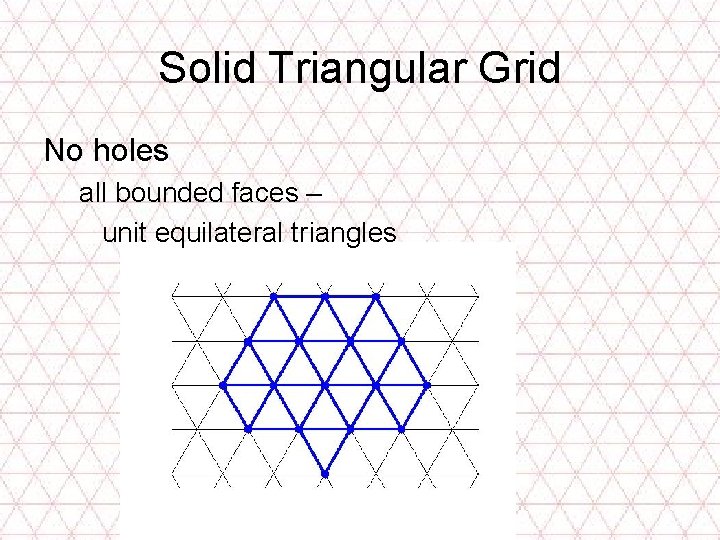
Solid Triangular Grid No holes all bounded faces – unit equilateral triangles

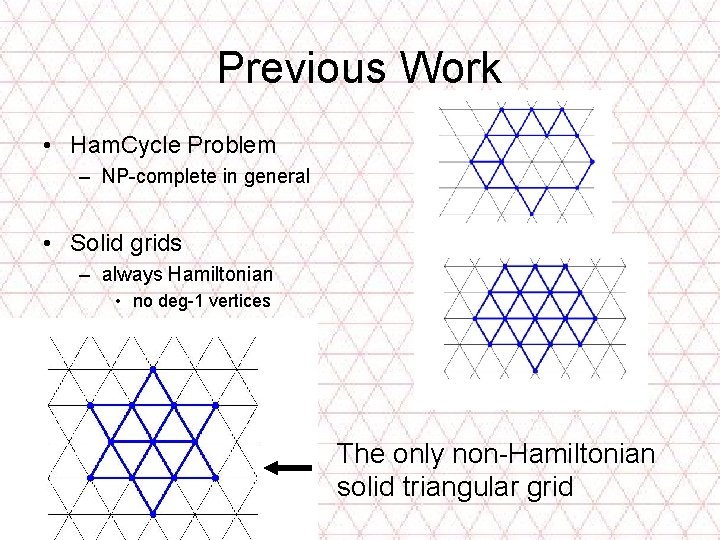
Previous Work • Ham. Cycle Problem – NP-complete in general • Solid grids – always Hamiltonian • no deg-1 vertices The only non-Hamiltonian solid triangular grid

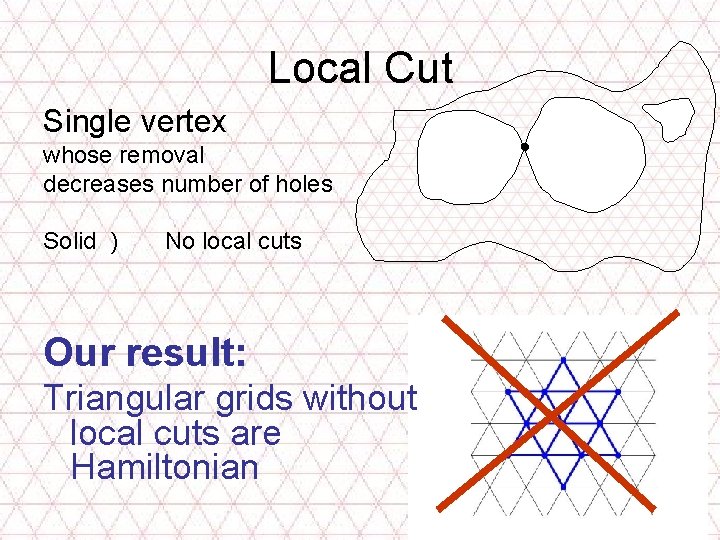
Local Cut Single vertex whose removal decreases number of holes Solid ) No local cuts Our result: Triangular grids without local cuts are Hamiltonian

Idea • B: – Cycle around the outer boundary – Cycles around holes’ boundaries • Use modifications – cycles go through all internal vertices • Exists “facing” rhombus – no local cuts = graph is “thick” – merge facing cycles • Decrease number of cycles • Get Hamiltonian Cycle

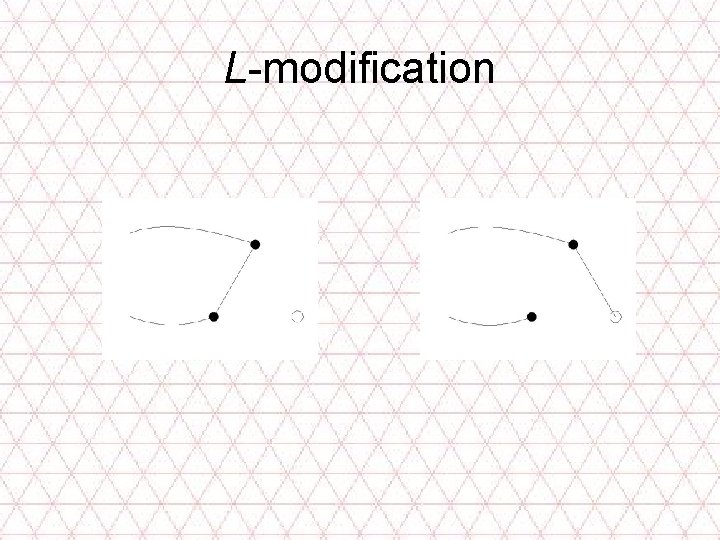
L-modification

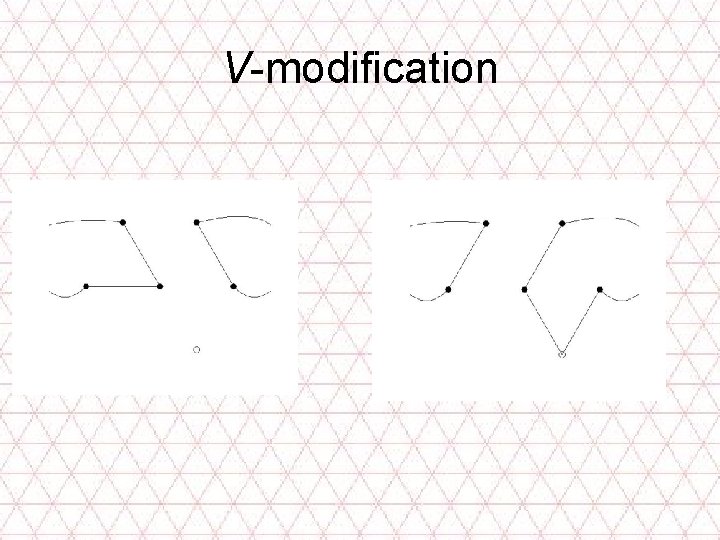
V-modification

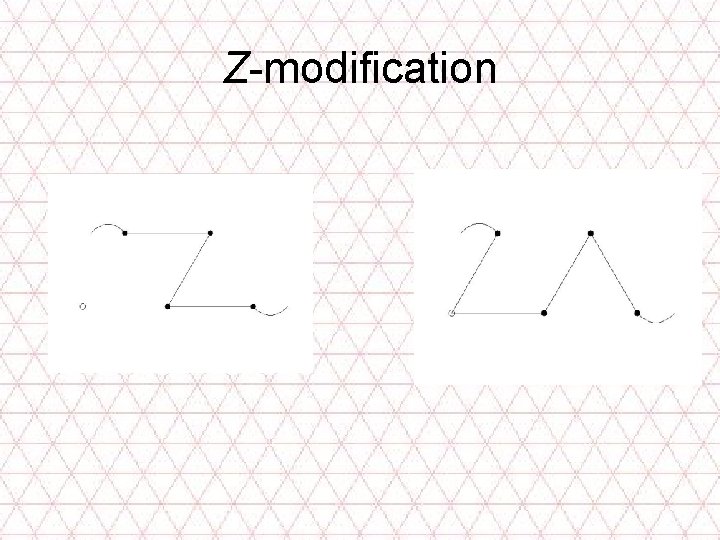
Z-modification

Priority: L , V , Z • L • V • Z

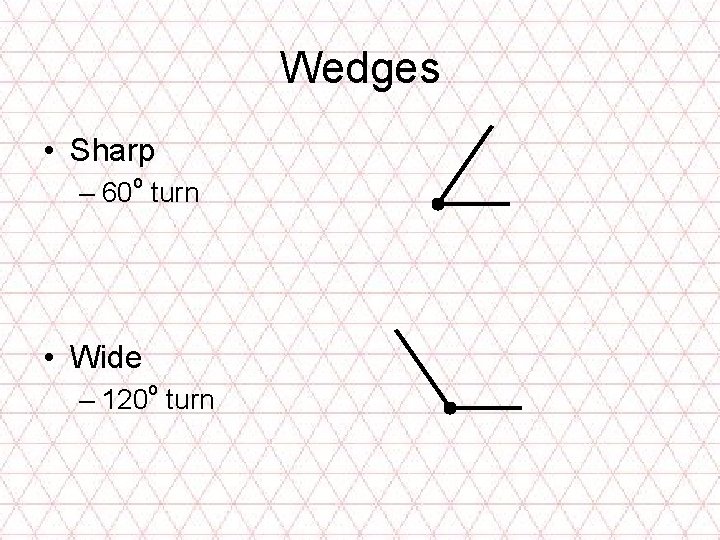
Wedges • Sharp o – 60 turn • Wide o – 120 turn

The Main Lemma Until B passes through ALL internal vertices – either L, V, or Z may be applied small print: unless G is the Star of David

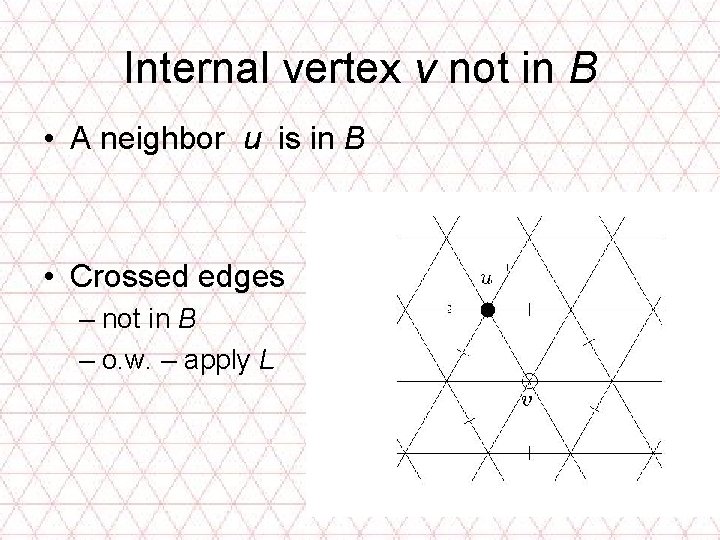
Internal vertex v not in B • A neighbor u is in B • Crossed edges – not in B – o. w. – apply L

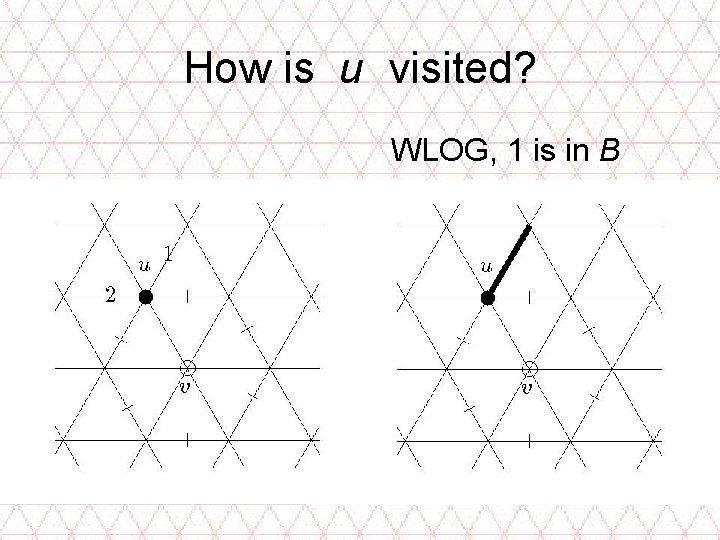
How is u visited? WLOG, 1 is in B

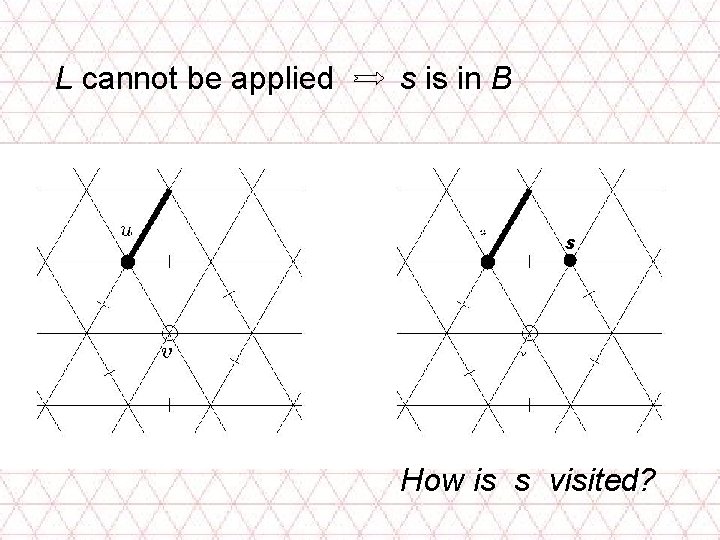
L cannot be applied s is in B s How is s visited?

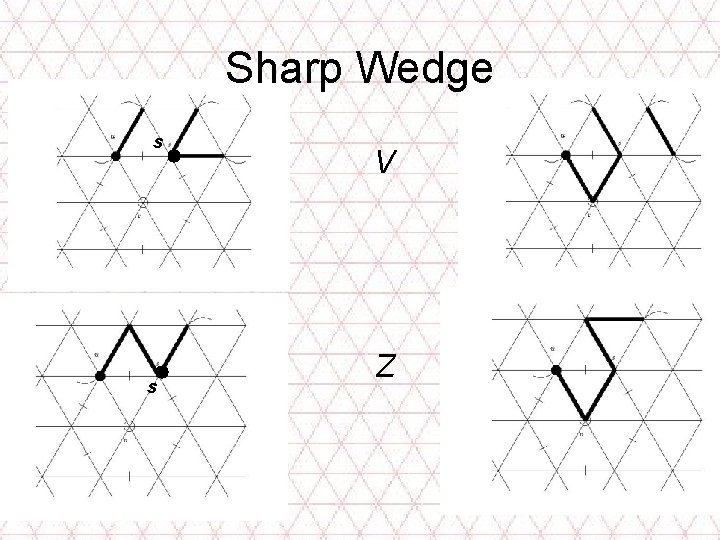
Sharp Wedge s s V Z

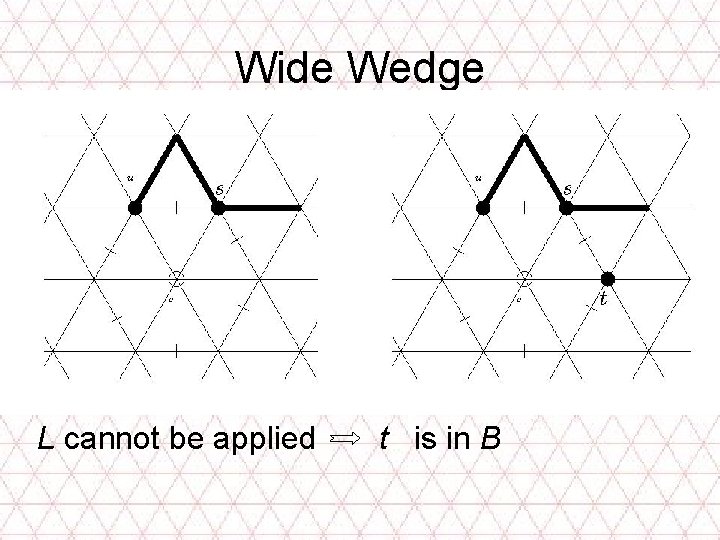
Wide Wedge L cannot be applied t is in B

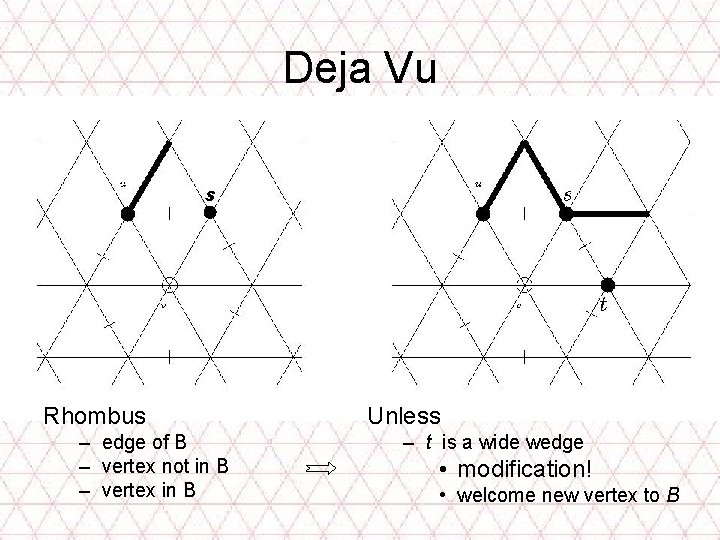
Deja Vu s Rhombus – edge of B – vertex not in B – vertex in B Unless – t is a wide wedge • modification! • welcome new vertex to B

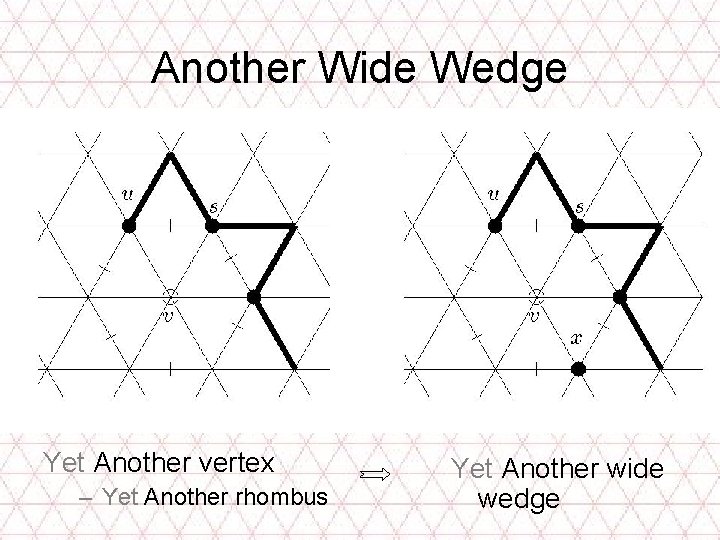
Another Wide Wedge Yet Another vertex – Yet Another rhombus Yet Another wide wedge

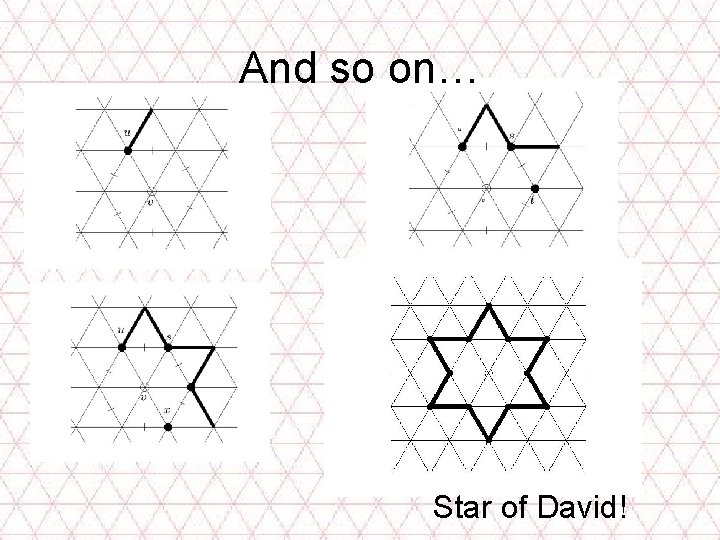
And so on… Star of David!

Cycle Cover → Ham. Cycle • Cycles around the outer boundary • Cycles around holes’ boundaries • Use modifications – cycles go through all internal vertices • Exists “facing” rhombus – no local cuts = graph is “thick” – merge facing cycles • Decrease number of cycles • Get Hamiltonian Cycle

Hamiltonian Cycles in High-Girth Graphs

Ham. Cycle Problem is NP-complete • Classic • Girth? – – 4 3 • NP-complete [GJ] [CLRS] [Garey, Johnson, Tarjan’ 76] – planar – cubic – girth-5 Higher girth?

Multi-Hamiltonicity • 1 HC 2 HCs cubic [Smith], any vert – odd-deg r-regular, r > 300 [Thomassen’ 98], r > 48 4 -regular? conjecture maxdeg ≥ f( maxdeg/mindeg ) bipartite, mindeg in a part = 3 • 1 HC exp(maxdeg) HCs [Thomason’ 78] [Ghandehari and Hatami] [Sheehan’ 75] [Horak and Stacho’ 00] [Thomassen’ 96] – bipartite • 1 HC cubic exp(girth) HCs or [Thomassen’ 96] bipartite, mindeg in a part = 4 Planar maxdeg 3, high-girth? >1 HC? Small # of HCs?

Our Contribution Planar maxdeg 3 arbitrarily large girth • Ham. Cycle Problem is NP-complete • Exactly 3 Ham. Cycles arbitrarly large # of vertices

The Other Tiling: Infinite Hexagonal Grid • Induced graphs – hexagonal grids Is Ham. Cycle Problem NP-hard for hexagonal grids?

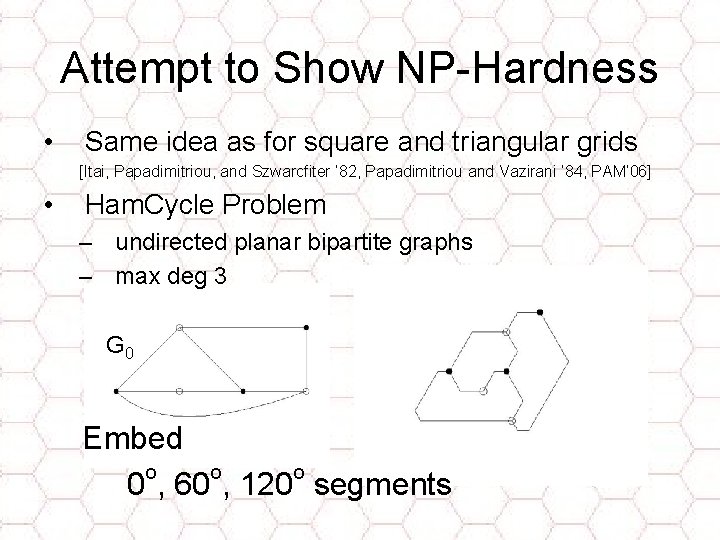
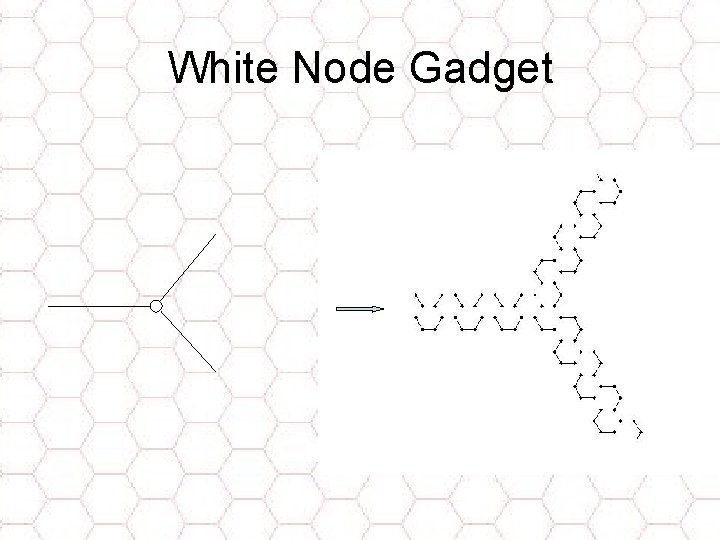
Attempt to Show NP-Hardness • Same idea as for square and triangular grids [Itai, Papadimitriou, and Szwarcfiter ‘ 82, Papadimitriou and Vazirani ’ 84, PAM’ 06] • Ham. Cycle Problem – undirected planar bipartite graphs – max deg 3 G 0 Embed o o o 0 , 60 , 120 segments

(Try to) Embed in Hex Grid

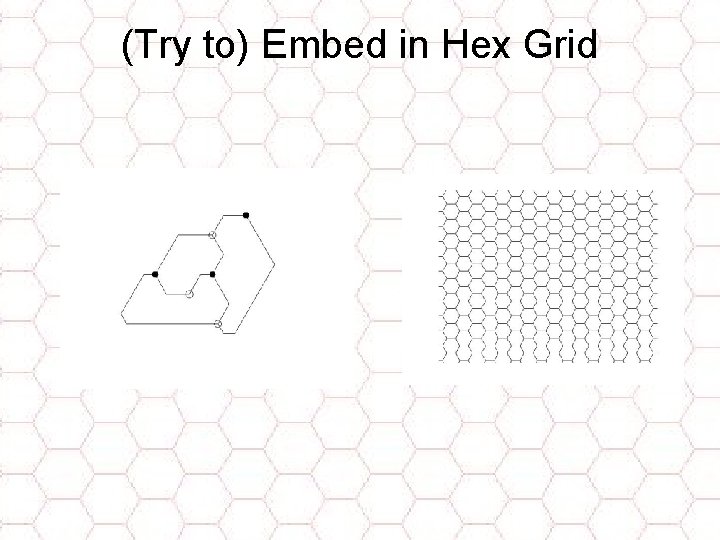
Edges – Tentacles

Traversing Tentacles

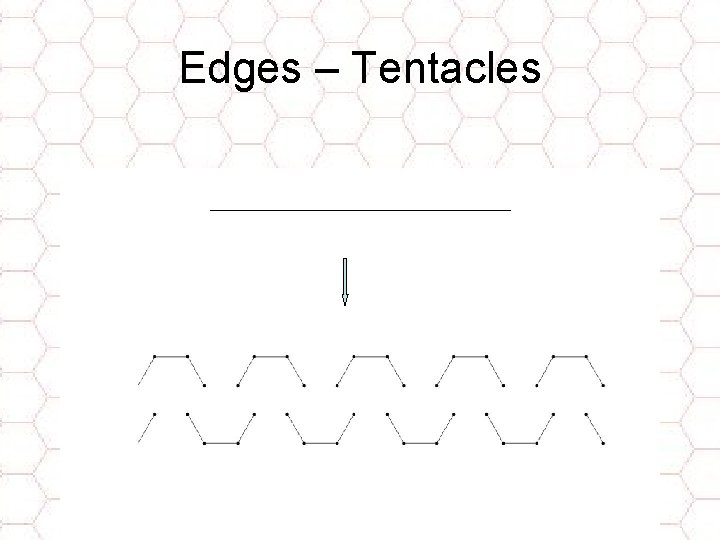
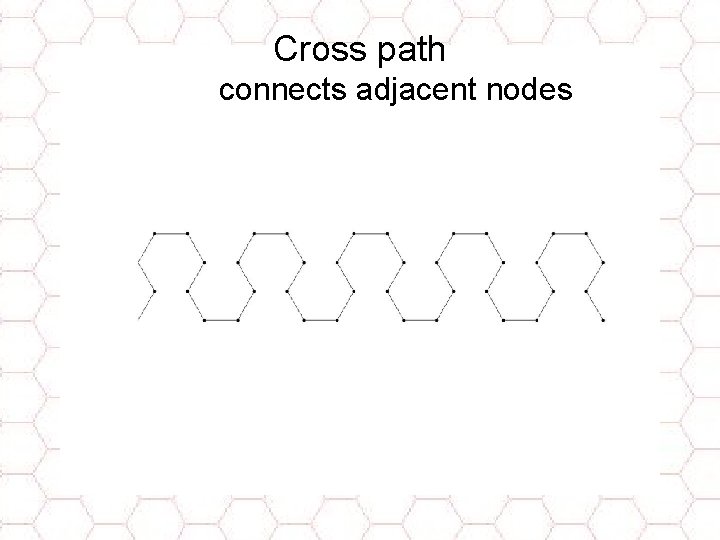
Cross path connects adjacent nodes

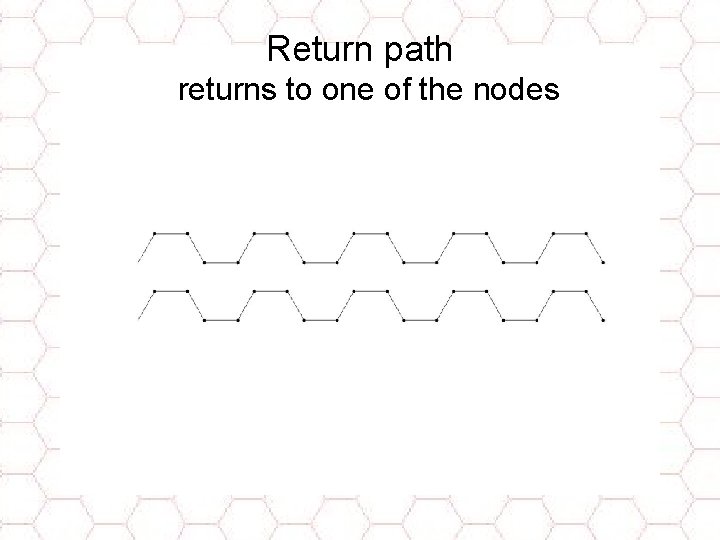
Return path returns to one of the nodes

White Node Gadget

Middle Vertex: 2 edges…

Middle Vertex: 2 edges…

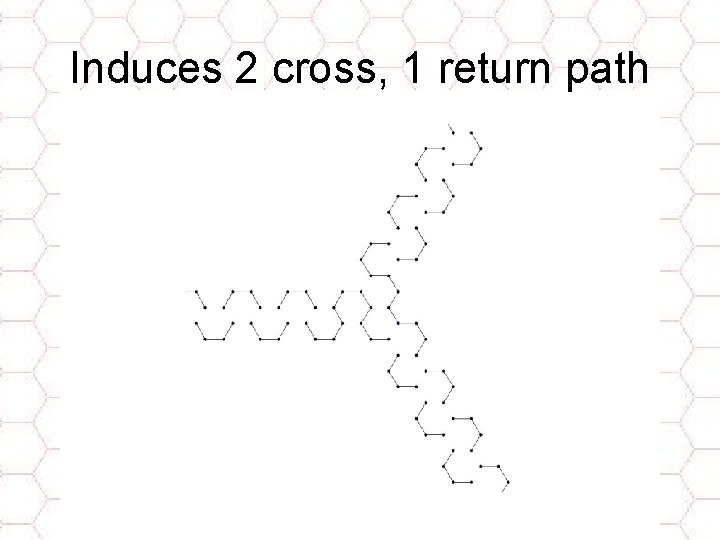
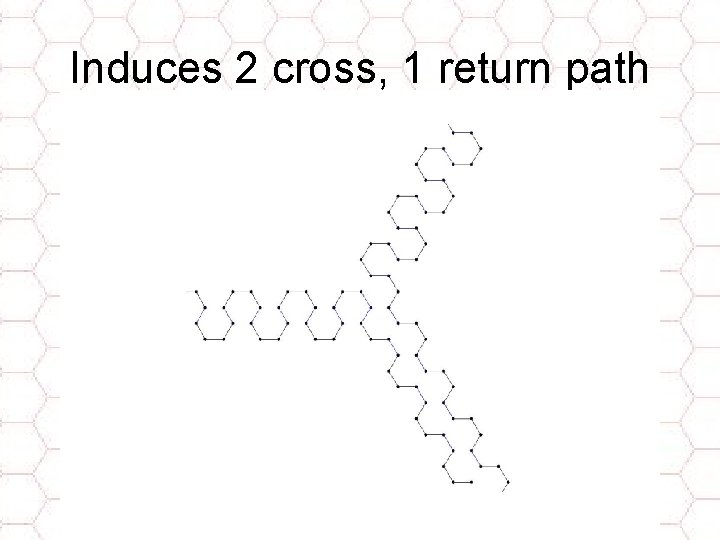
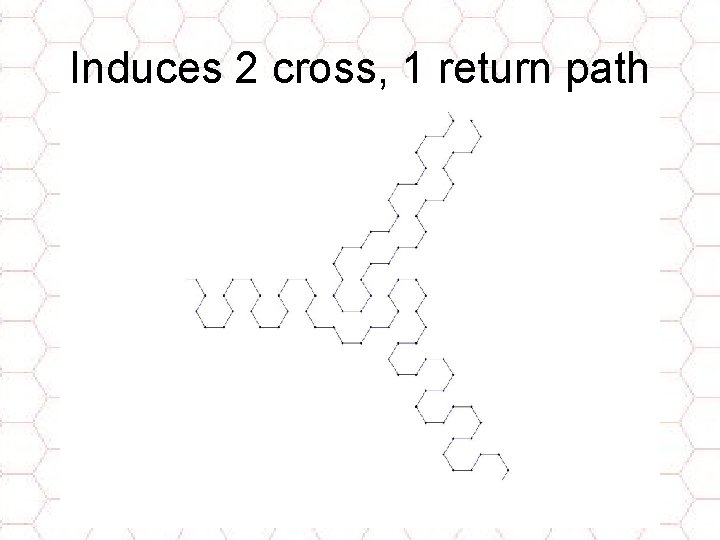
Induces 2 cross, 1 return path

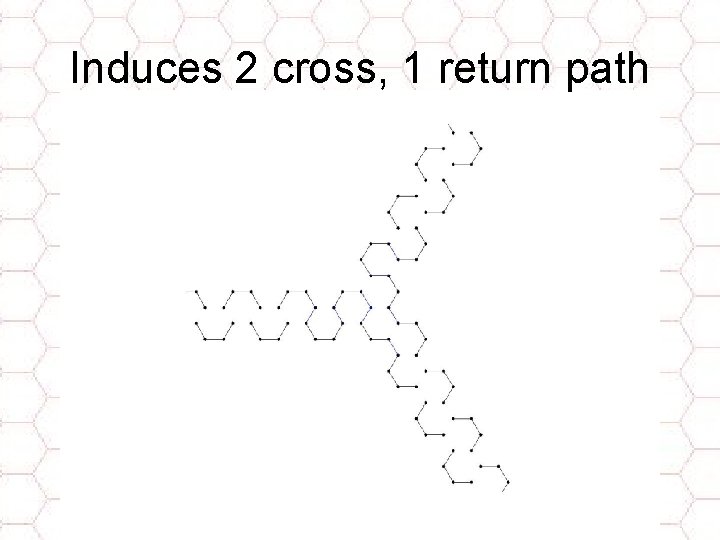
Induces 2 cross, 1 return path

Induces 2 cross, 1 return path

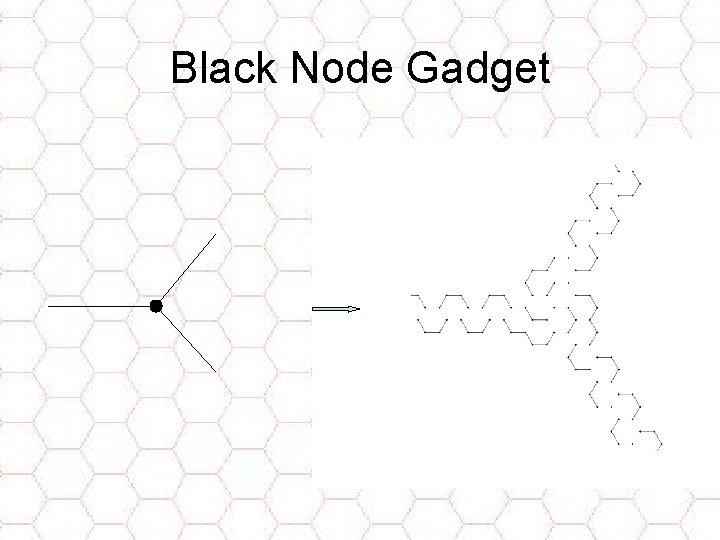
Black Node Gadget

Middle Vertex: 2 edges…

Middle Vertex: 2 edges…

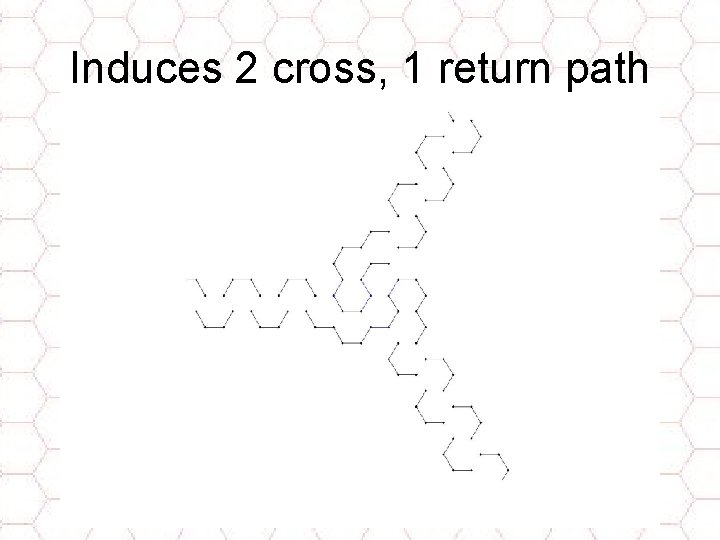
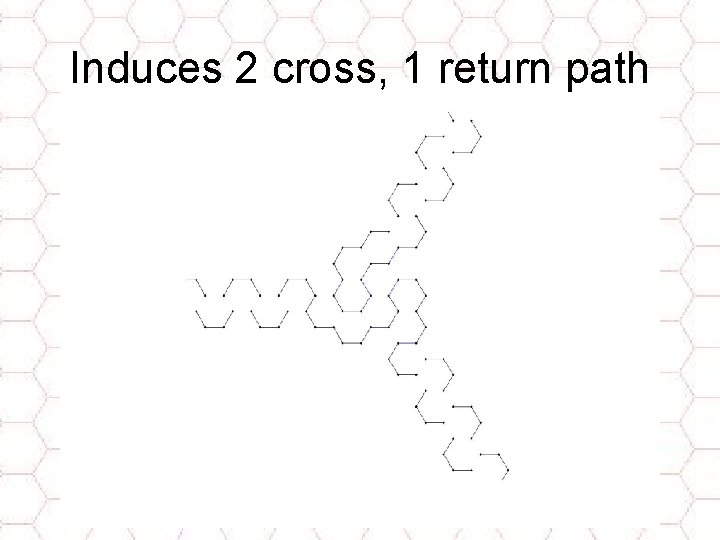
Induces 2 cross, 1 return path

Induces 2 cross, 1 return path

Induces 2 cross, 1 return path

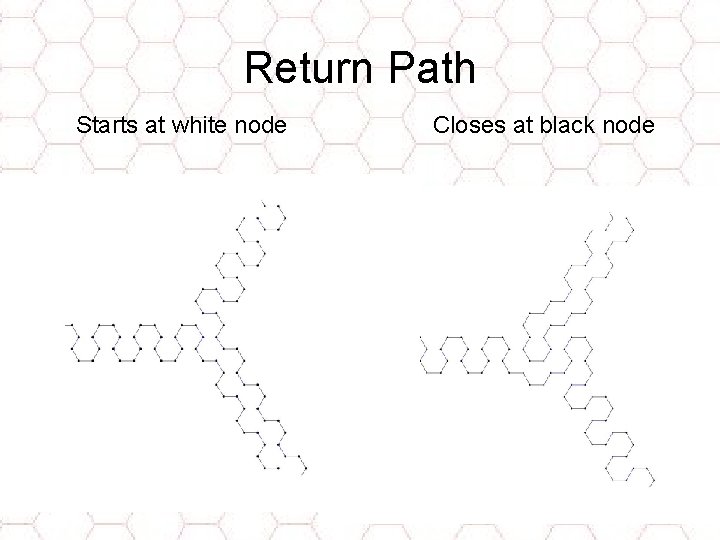
Return Path Starts at white node Closes at black node

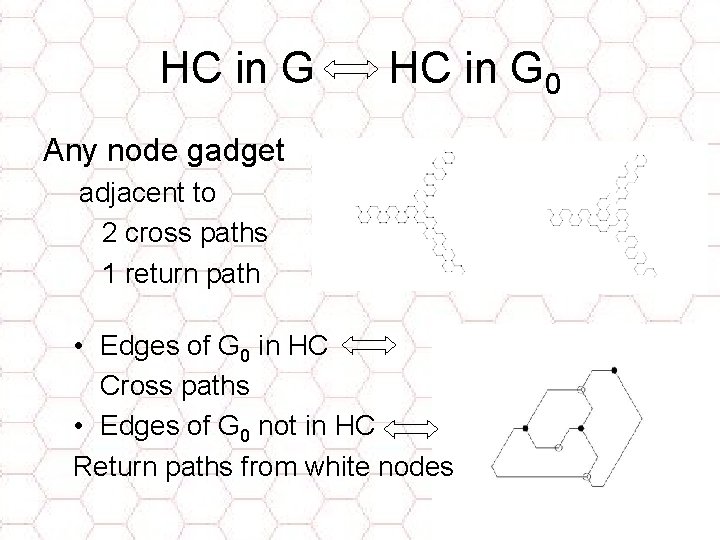
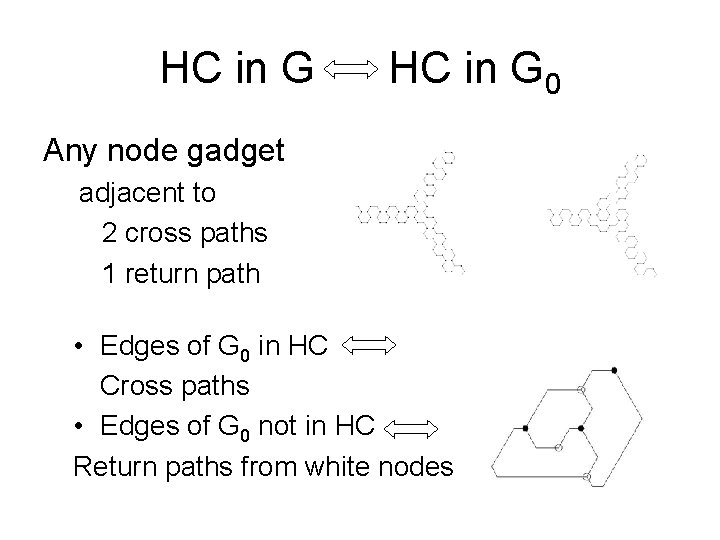
HC in G 0 Any node gadget adjacent to 2 cross paths 1 return path • Edges of G 0 in HC Cross paths • Edges of G 0 not in HC Return paths from white nodes

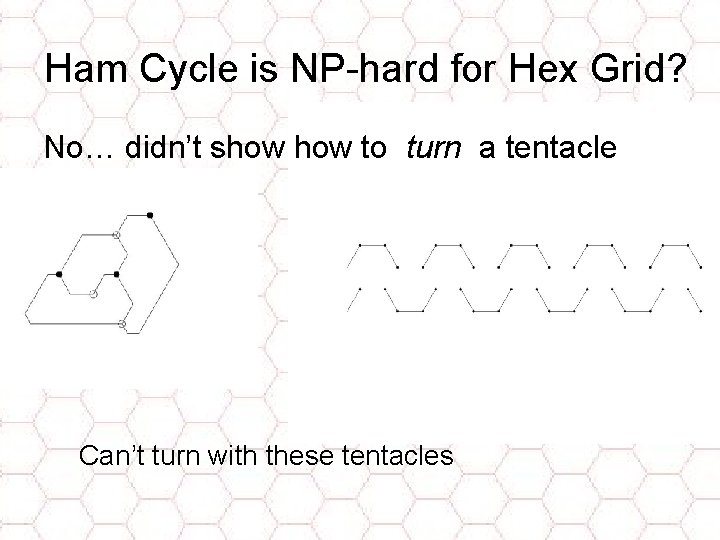
Ham Cycle is NP-hard for Hex Grid? No… didn’t show to turn a tentacle Can’t turn with these tentacles

No Longer in a Hex Grid

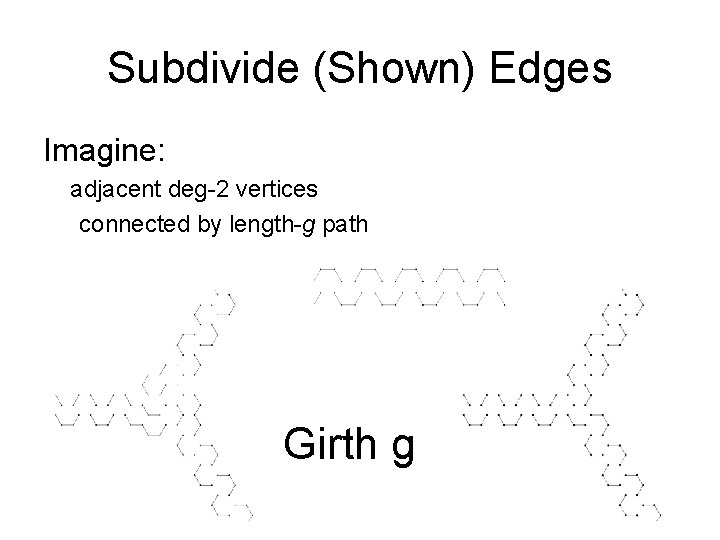
Subdivide (Shown) Edges Imagine: adjacent deg-2 vertices connected by length-g path Girth g

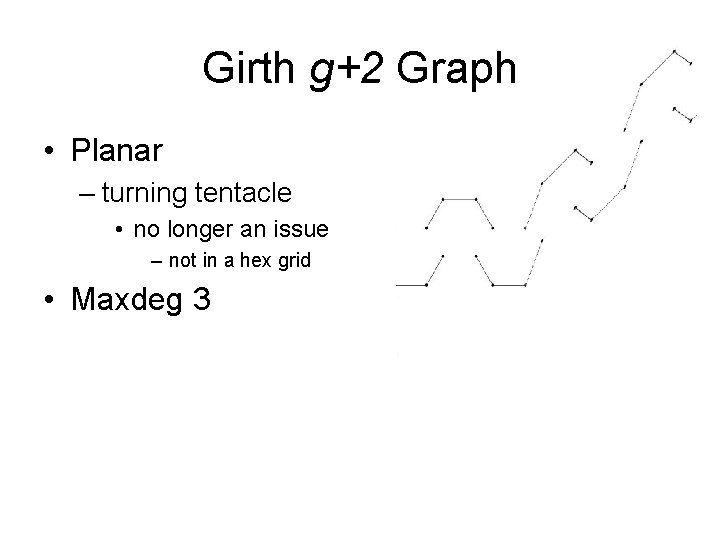
Girth g+2 Graph • Planar – turning tentacle • no longer an issue – not in a hex grid • Maxdeg 3

HC in G 0 Any node gadget adjacent to 2 cross paths 1 return path • Edges of G 0 in HC Cross paths • Edges of G 0 not in HC Return paths from white nodes

Theorem 1 For any g ≥ 6 Ham. Cycle is NP-hard in planar deg ≤ 3 non-bipartite girth-g graphs

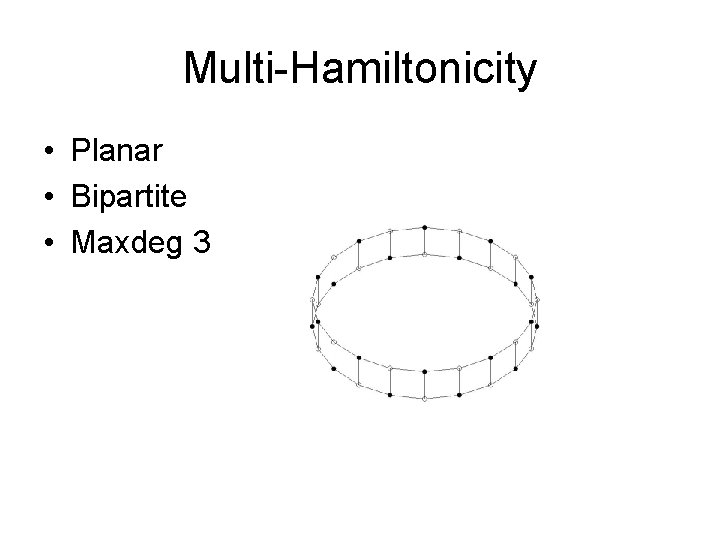
Multi-Hamiltonicity • Planar • Bipartite • Maxdeg 3

Exactly 3 Ham. Cycles

Theorem 2 For any g ≥ 6 exists planar deg ≤ 3 non-bipartite girth-g graph with exactly 3 Ham. Cycles

Summary • Trangular grids no local cut ) Hamiltonian • maxdeg-3 planar girth-g – Ham. Cycle Problem is NP-complete – exists graphs with exactly 3 Ham. Cycles

Open • Ham. Cycle Problem in hexagonal grids