Paths and Circuits Lecture 52 Section 11 2

The Seven Bridges of Königsberg ¢ In the city of Königsberg, two branches of

The Seven Bridges of Königsberg ¢ There were seven bridges crossing the river at

The Seven Bridges of Königsberg ¢ The challenge was to start at one point,

Euler’s Solution ¢ Euler abstracted the bridges as a graph with four vertices and

Euler’s Solution ¢ Each vertex represents a land mass and each edge represents a

Walks and Paths A walk from vertex v to vertex w is a finite

Walks and Paths A simple path is a path that does not repeat any

Synopsis walk = from A to B, no restrictions. ¢ path = walk, no

Euler Circuits An Euler circuit is a circuit that contains every vertex and every

Connected Graphs A graph is connected if, for every pair of vertices v and

Euler’s Solution Theorem: A graph has an Euler circuit if and only if it

The Two Bridges of Ashland ¢ At Randolph-Macon College, they have been trying to

Proof ¢ Proof ( ): Suppose a graph G has an Euler circuit. l

Proof Thus, v had an even number of edges. l Obviously, G must be

Proof ¢ Proof ( ): Now suppose that G is connected and that every

Proof w has even degree, so there is at least one more edge available

Proof Suppose there are edges that were not used. l Follow the original circuit

Proof Continue in this way, splicing circuits into the existing circuit, until there are

Euler Paths Theorem: A graph G has an Euler path from v to w

Hamiltonian Circuits A Hamiltonian circuit is a simple circuit that includes every vertex of

Hamiltonian Circuits ¢ Theorem: If a graph G has a nontrivial Hamiltonian circuit, then

Hamiltonian Circuits ¢ The following graph does not have a Hamiltonian circuit.

Slides: 64

Download presentation

Paths and Circuits Lecture 52 Section 11. 2 Wed, Apr 26, 2006

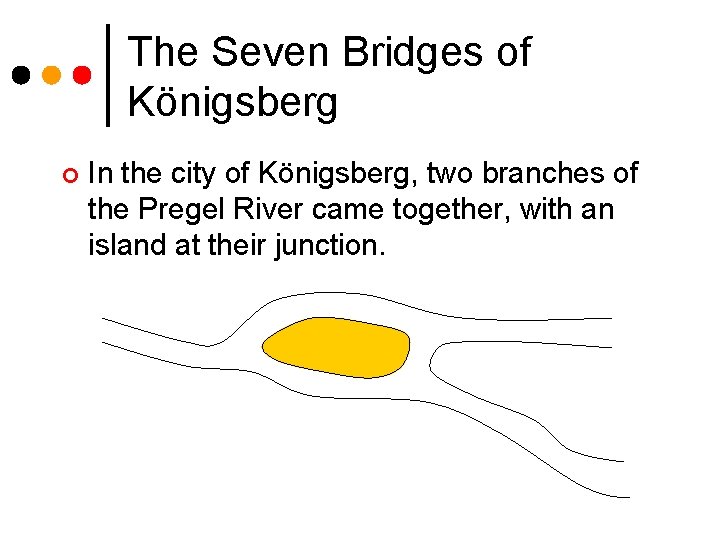
The Seven Bridges of Königsberg ¢ In the city of Königsberg, two branches of the Pregel River came together, with an island at their junction.

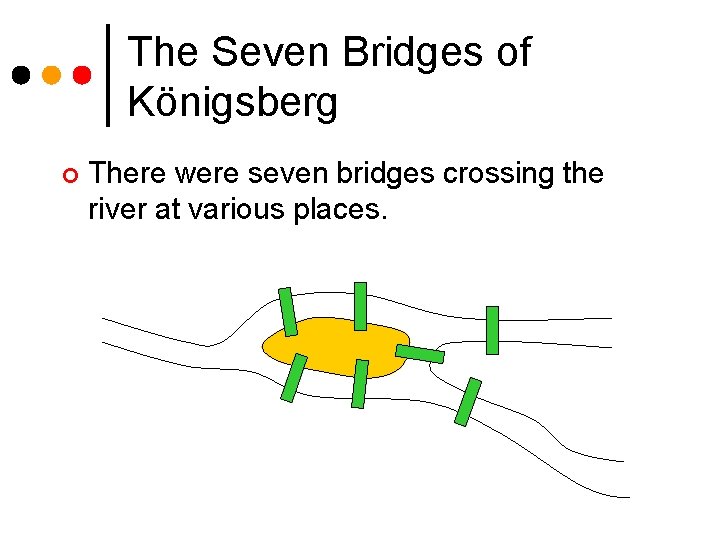
The Seven Bridges of Königsberg ¢ There were seven bridges crossing the river at various places.

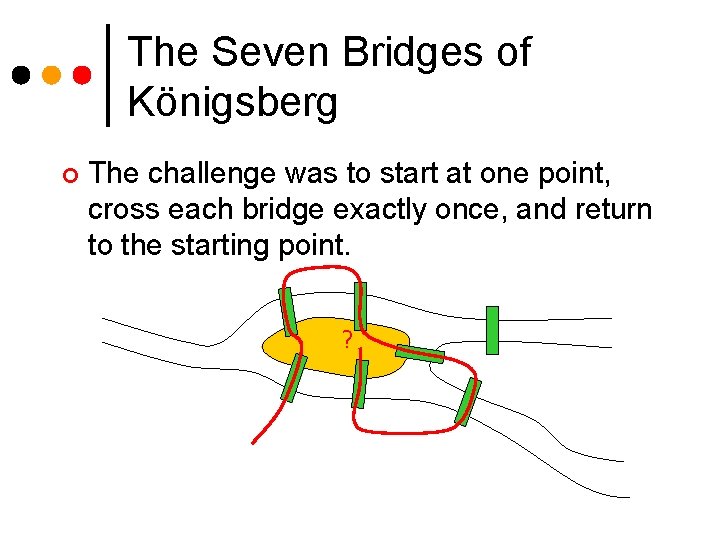
The Seven Bridges of Königsberg ¢ The challenge was to start at one point, cross each bridge exactly once, and return to the starting point. ?

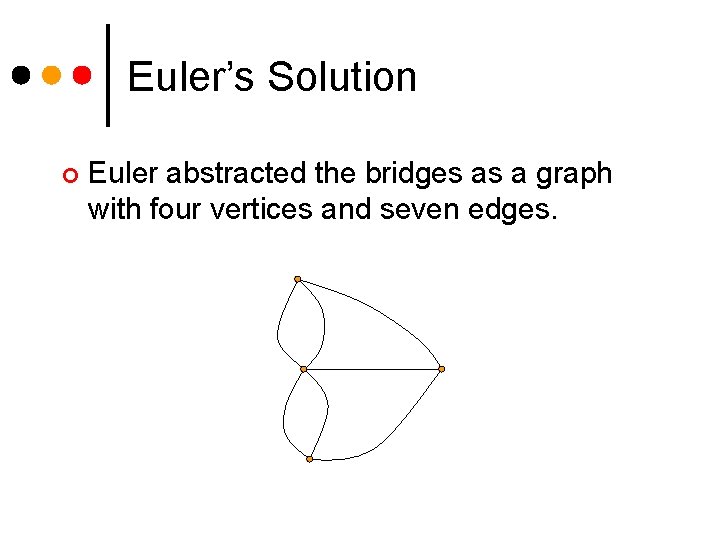
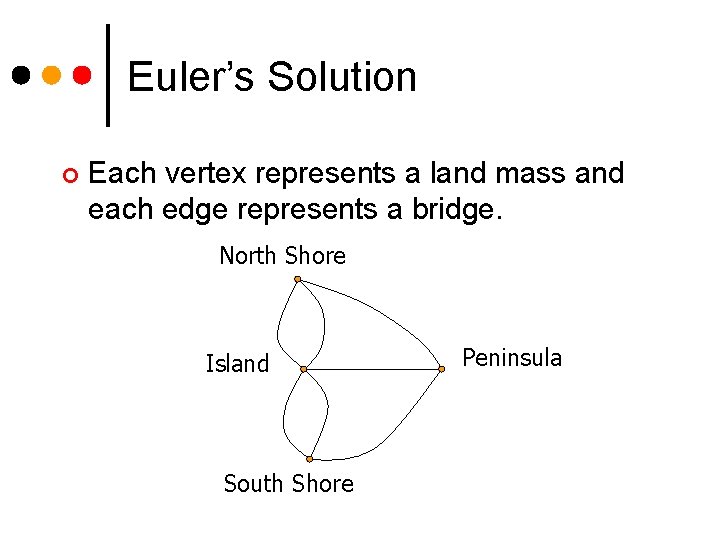
Euler’s Solution ¢ Euler abstracted the bridges as a graph with four vertices and seven edges.

Euler’s Solution ¢ Each vertex represents a land mass and each edge represents a bridge. North Shore Island South Shore Peninsula

Walks and Paths A walk from vertex v to vertex w is a finite alternating sequence of adjacent vertices and edges from v to w: v 0 e 1 v 1 e 2 … en – 1 vn – 1 en vn, where v 0 = v and vn = w. ¢ A path from v to w is a walk that does not repeat any edge. ¢

Walks and Paths A simple path is a path that does not repeat any vertices. ¢ A closed walk is a walk that starts and ends at the same vertex. ¢ A circuit is a closed path. ¢ A simple circuit is a circuit that does not repeat any vertex. ¢

Synopsis walk = from A to B, no restrictions. ¢ path = walk, no repeated edge. ¢ closed = from A to A. ¢ circuit = closed walk. ¢ simple = no repeated vertex. ¢

Euler Circuits An Euler circuit is a circuit that contains every vertex and every edge of the graph. ¢ The problem of the Seven Bridges of Königsberg is to find an Euler circuit. ¢

Connected Graphs A graph is connected if, for every pair of vertices v and w, there is a walk from v to w. ¢ A connected component of a graph is a maximal connected subgraph. ¢

Euler’s Solution Theorem: A graph has an Euler circuit if and only if it is connected and every vertex has even degree. ¢ Thus, an Euler circuit over the Seven Bridges of Königsberg does not exist. ¢

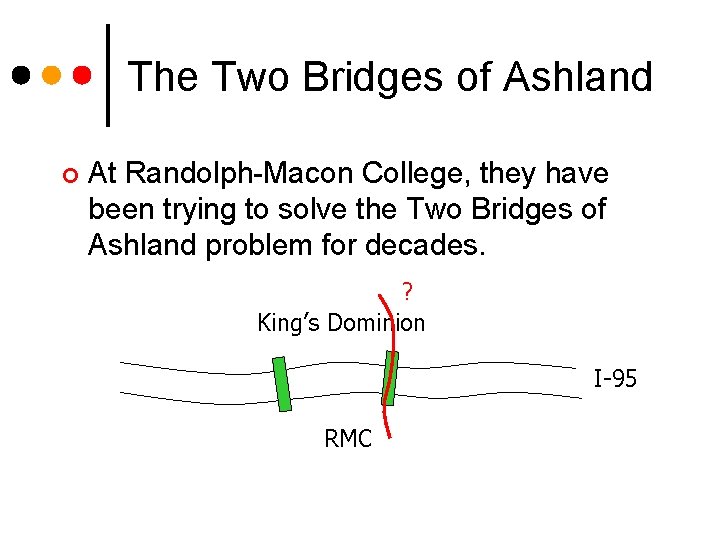
The Two Bridges of Ashland ¢ At Randolph-Macon College, they have been trying to solve the Two Bridges of Ashland problem for decades. ? King’s Dominion I-95 RMC

Proof ¢ Proof ( ): Suppose a graph G has an Euler circuit. l Let v V(G). l Then as we travel the circuit, each time we pass through v, we “use up” two of the edges incident to v. l When we finish the circuit, we have used all the edges incident to v. l

Proof Thus, v had an even number of edges. l Obviously, G must be connected. l

Proof ¢ Proof ( ): Now suppose that G is connected and that every vertex of G has even degree. l Choose a vertex v at which to begin. l deg(v) > 0 since G is connected, so follow one of the edges incident to v. l Let w be the next vertex. l We used one of w’s edges to get there. l

Proof w has even degree, so there is at least one more edge available that we can follow. l This happens at every vertex that we visit. l Thus, the circuit is forced to terminate only when we return to the starting vertex v. l This procedure alone does not necessarily produce an Euler circuit. l

Proof Suppose there are edges that were not used. l Follow the original circuit until a vertex is reached that is incident to one of the unused edges. l Apply the original procedure to produce a circuit that starts and ends at this vertex. l “Splice” it into the original circuit. l

Proof Continue in this way, splicing circuits into the existing circuit, until there are no unused edges remaining. l The result is an Euler circuit. l

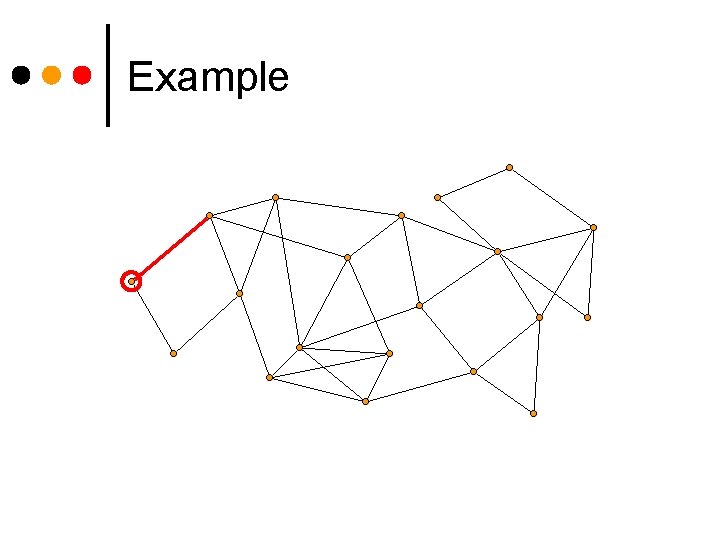
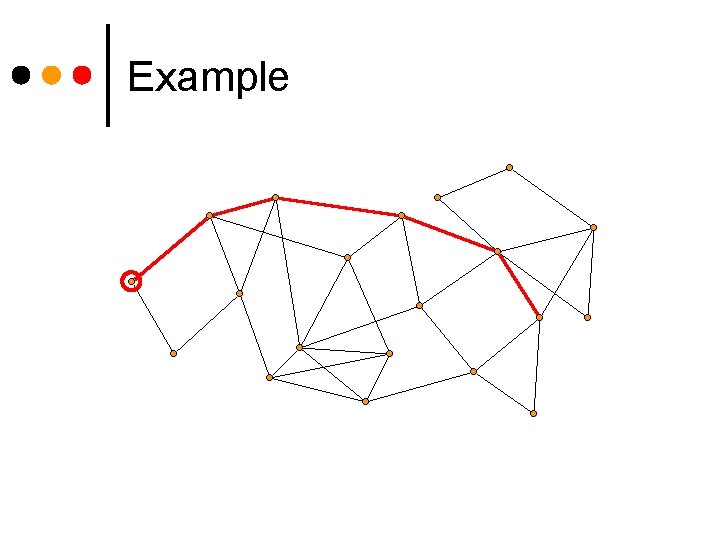
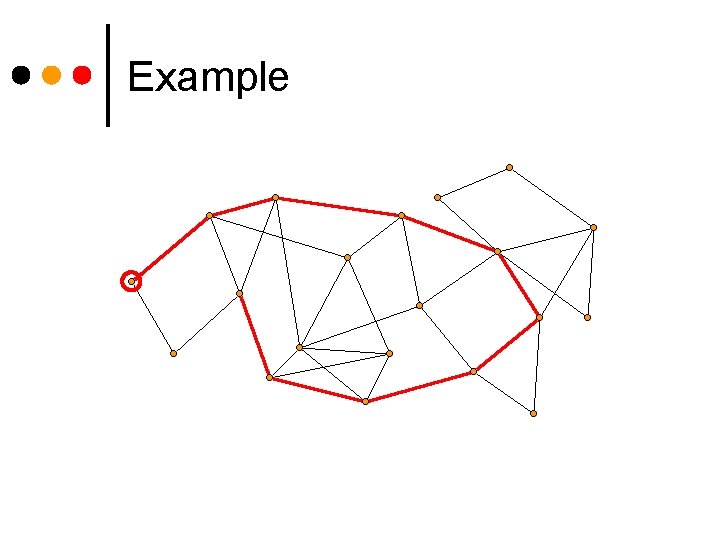
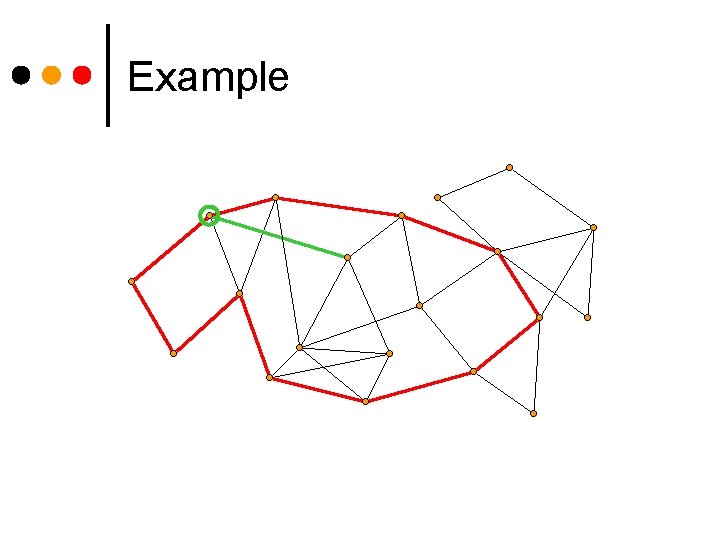
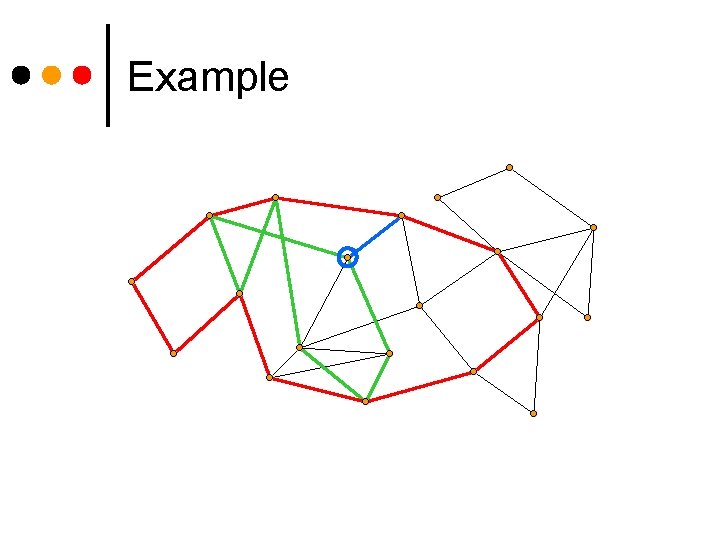
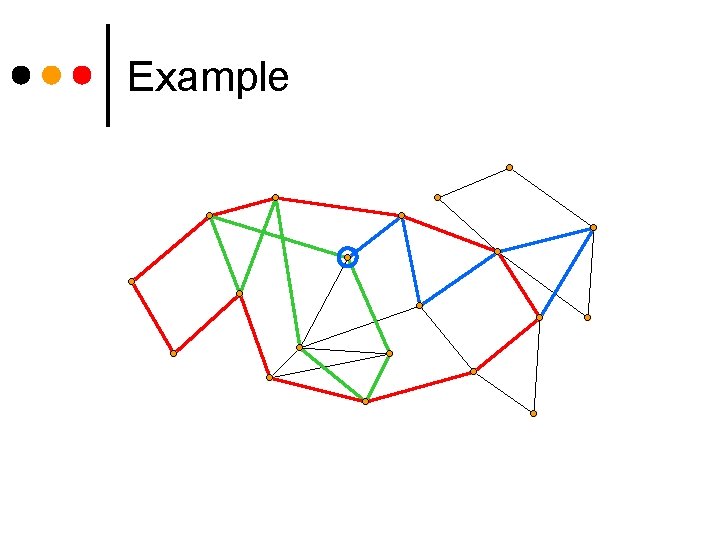
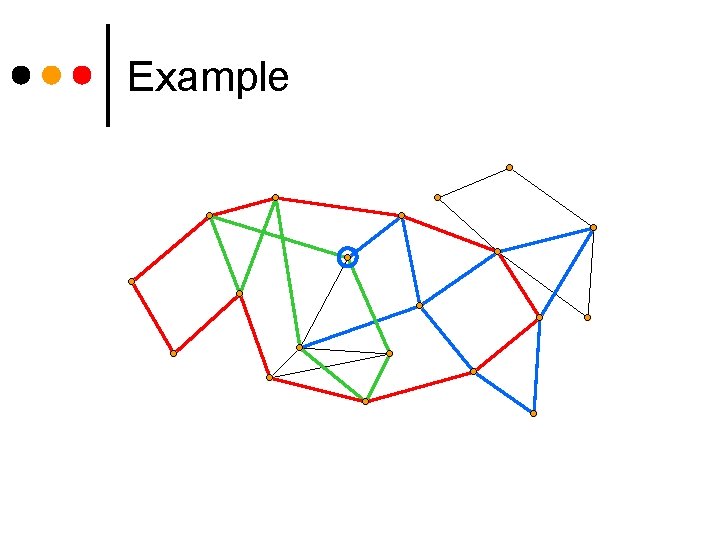
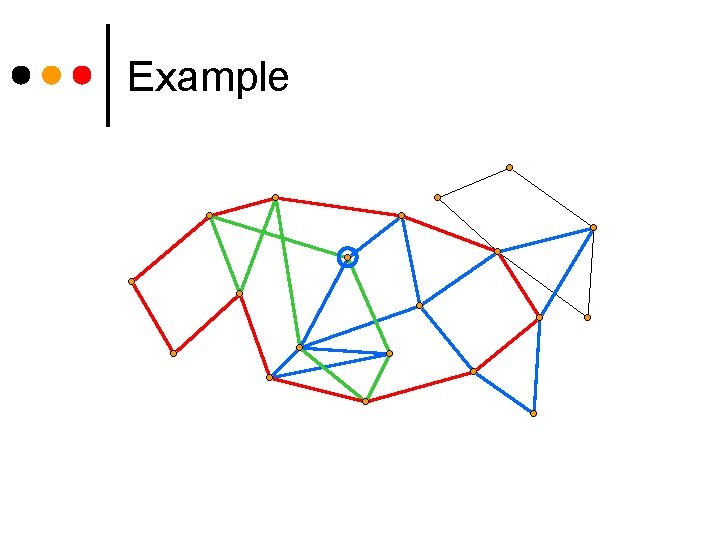
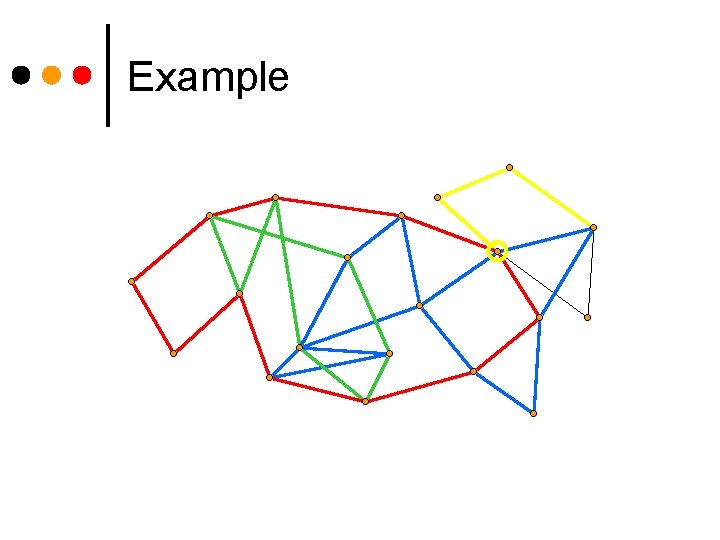
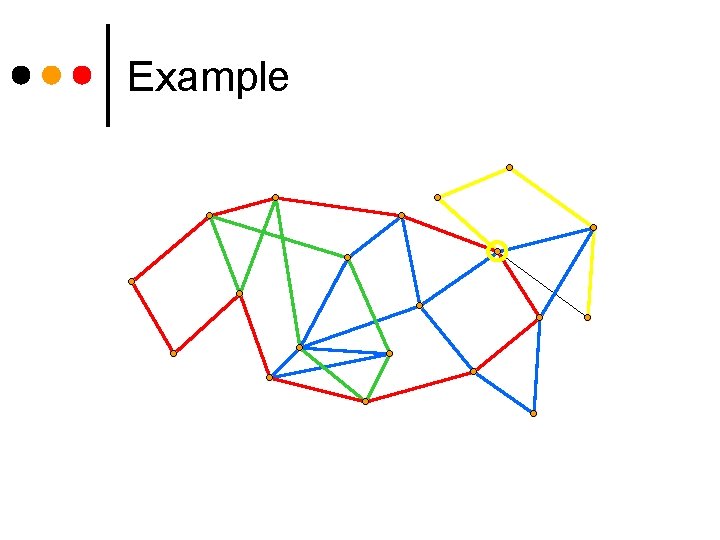
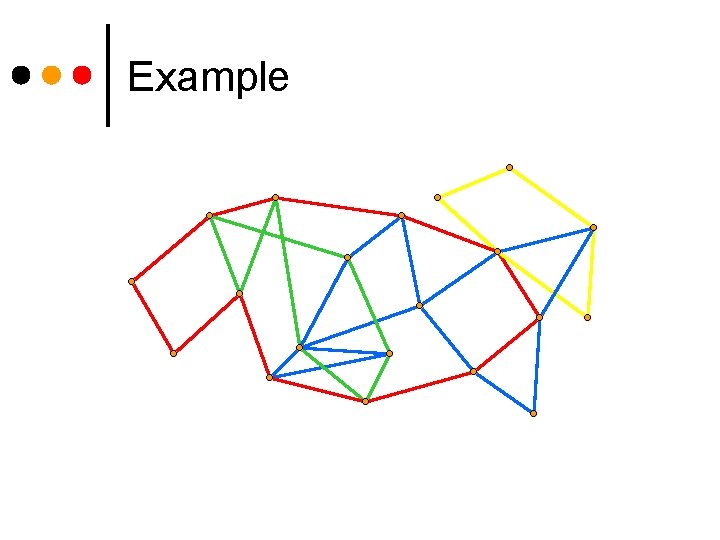
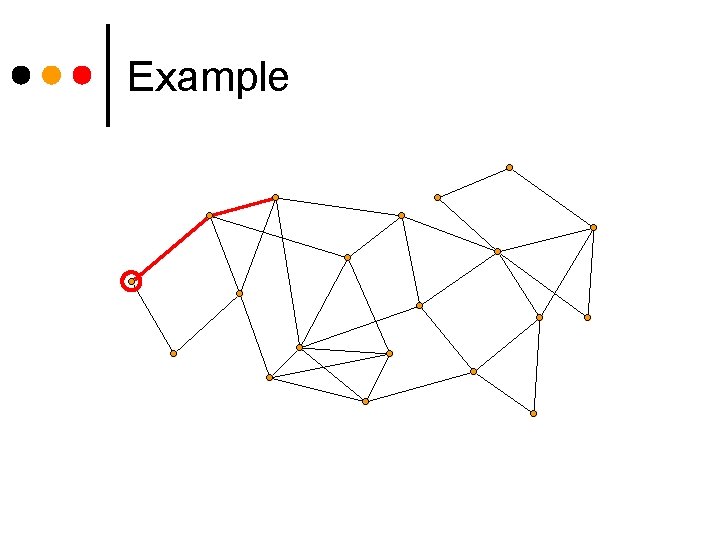
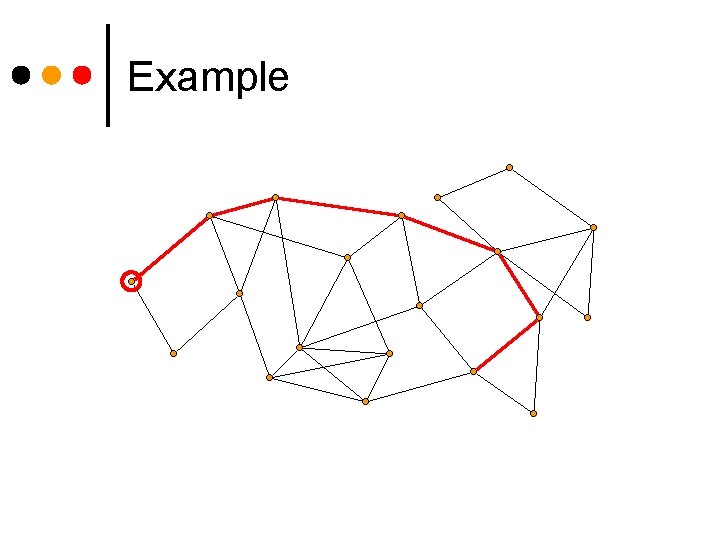
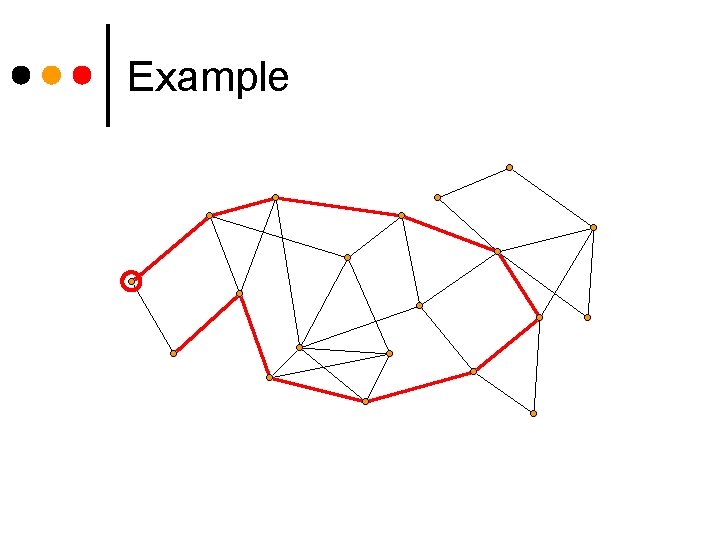
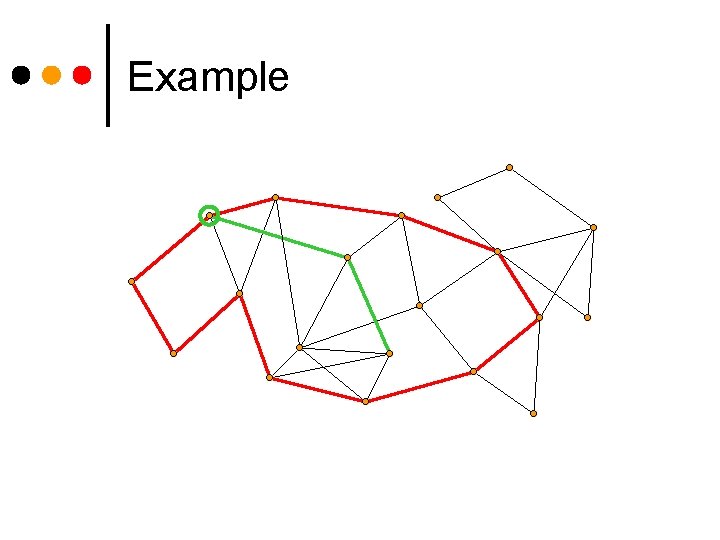
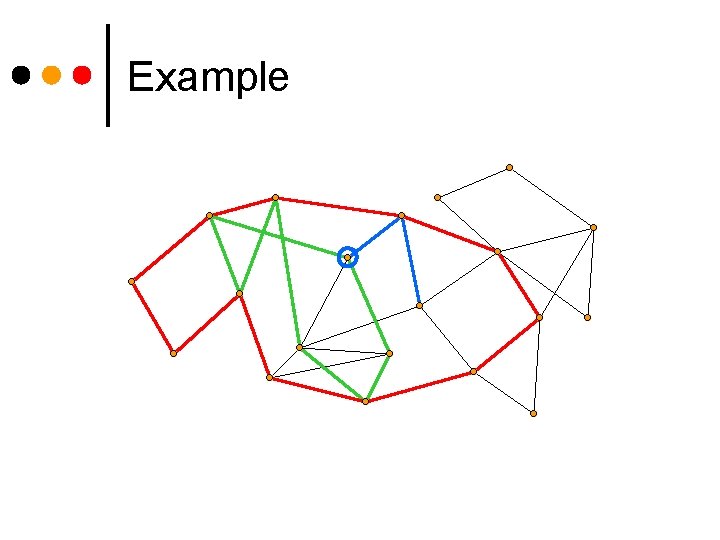
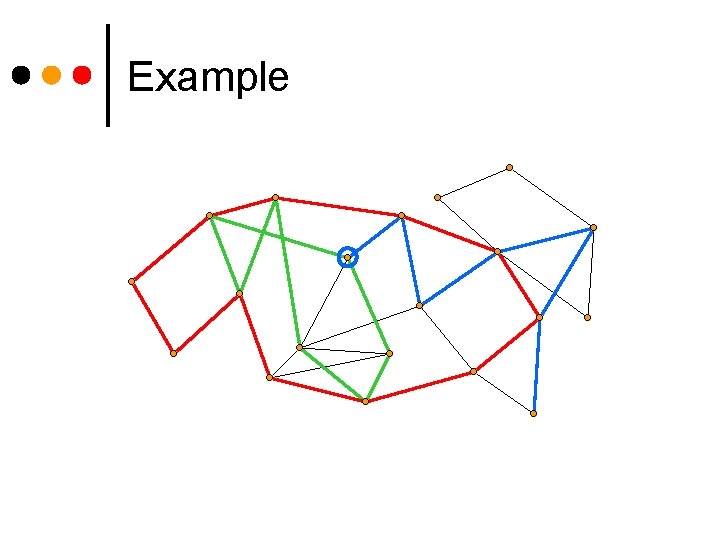
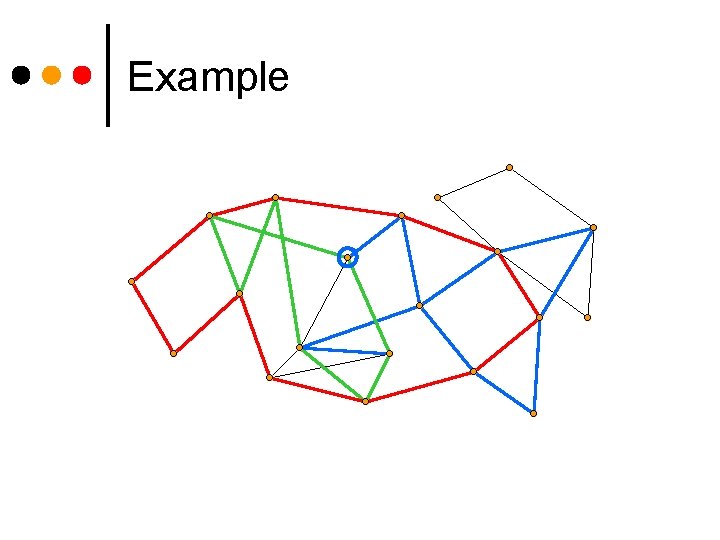
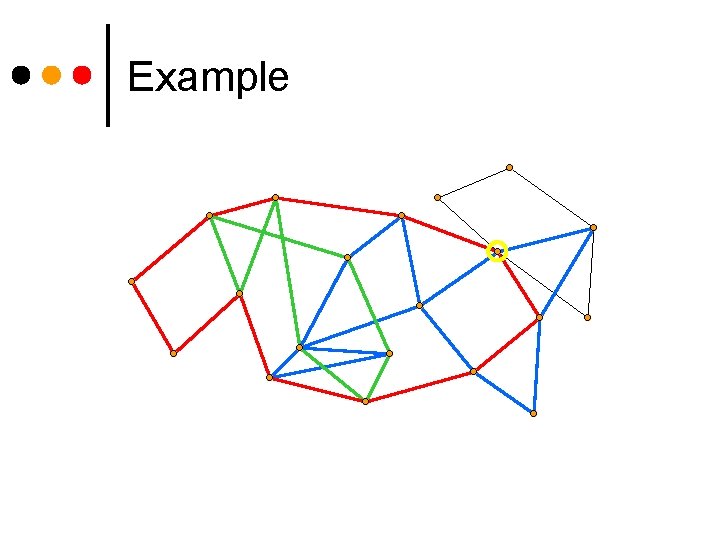
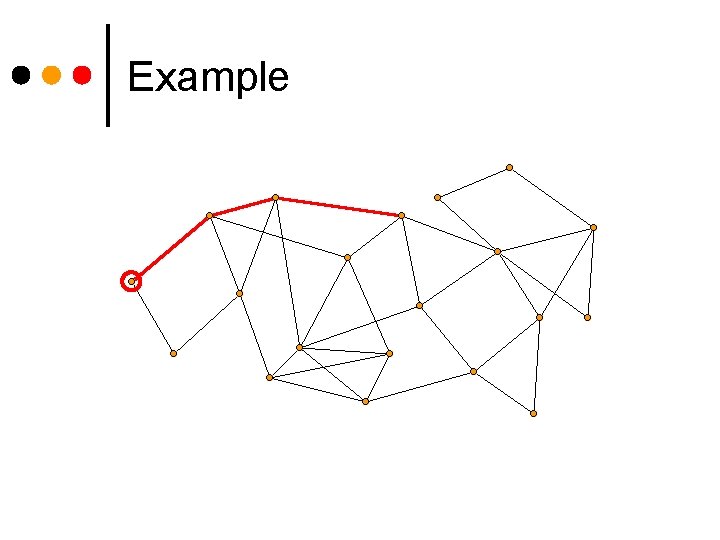
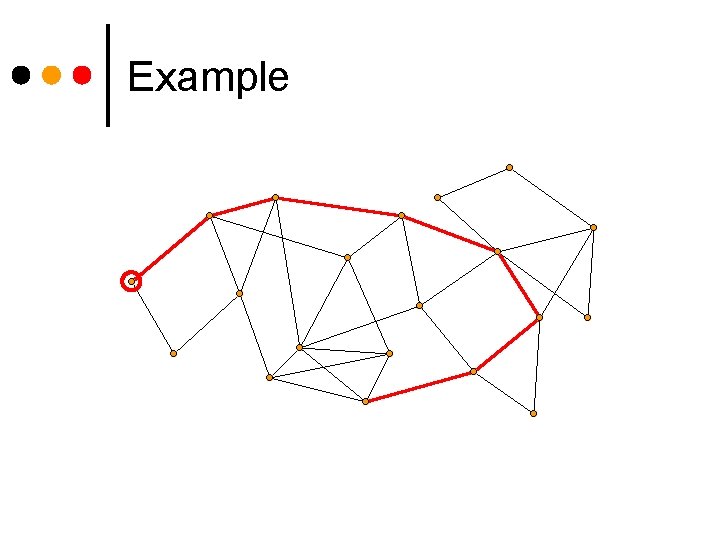
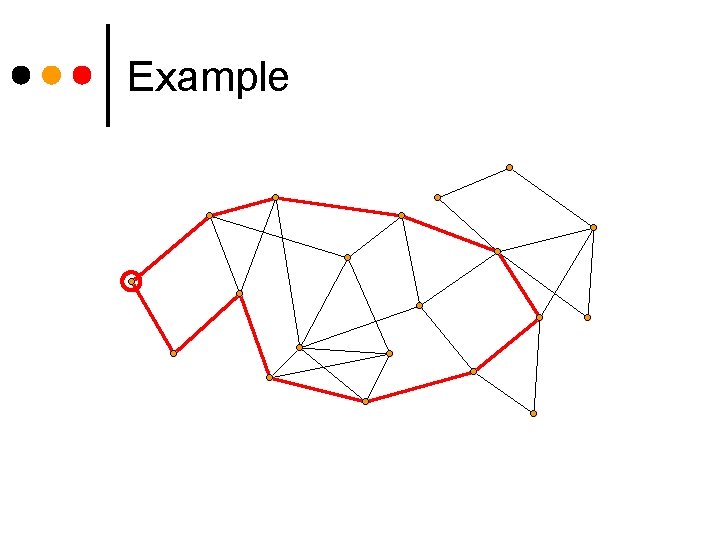
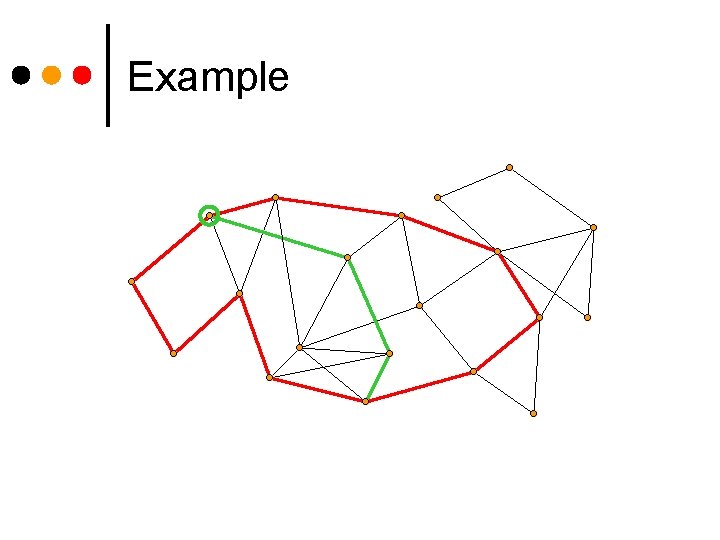
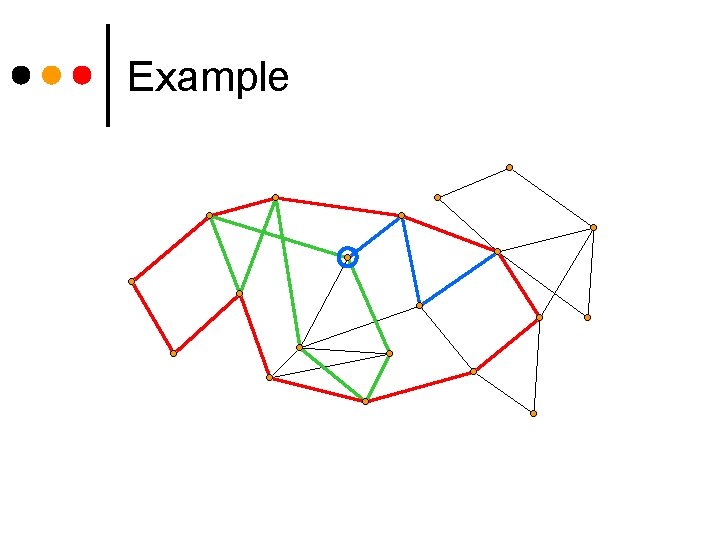
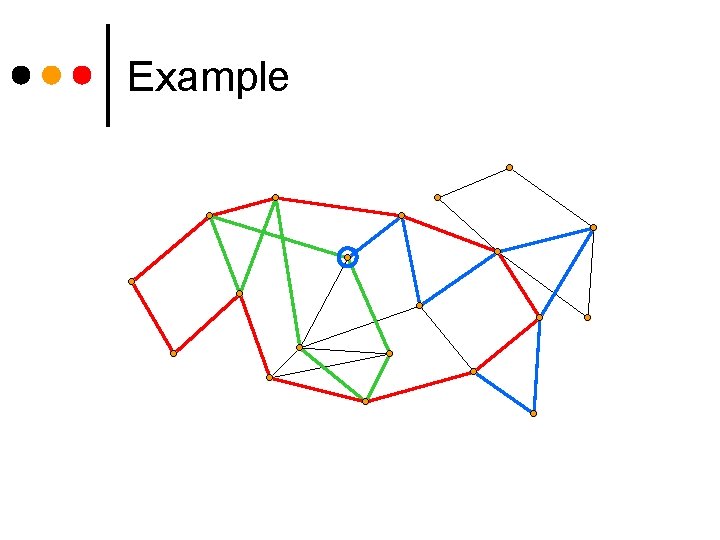
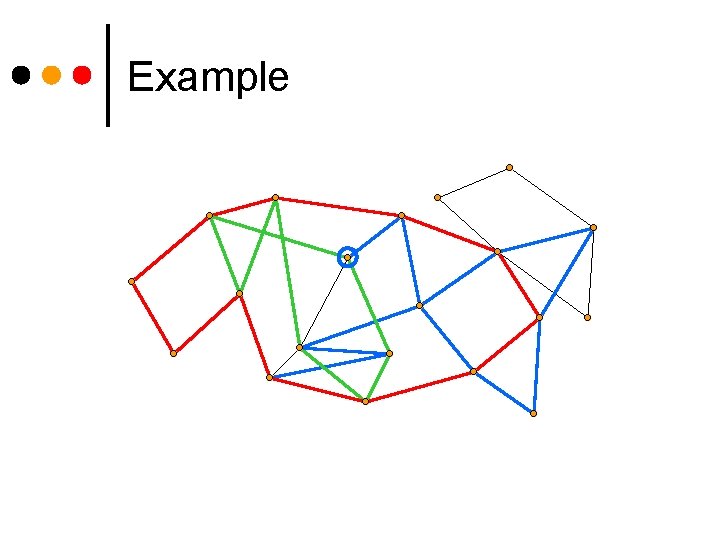
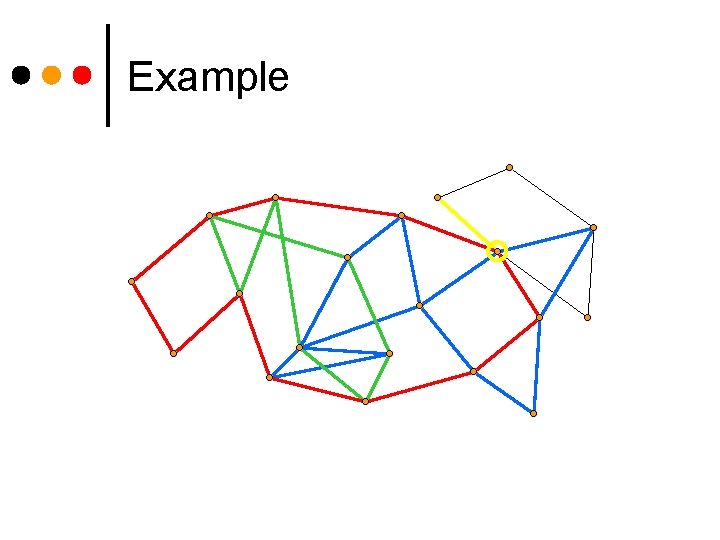
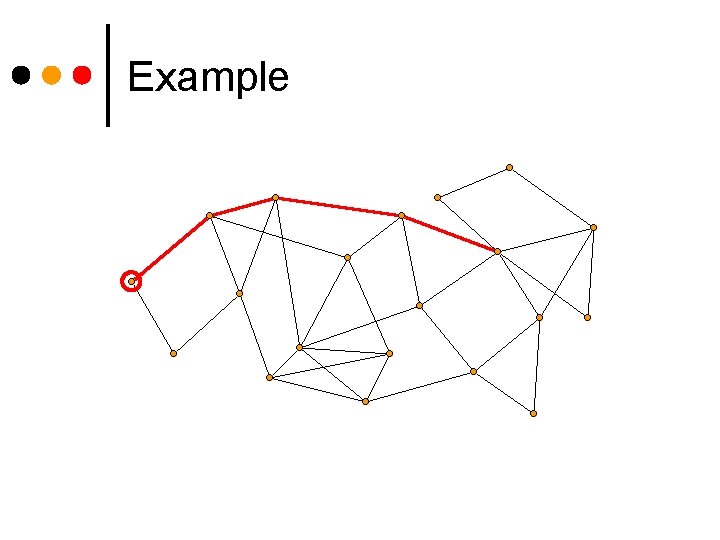
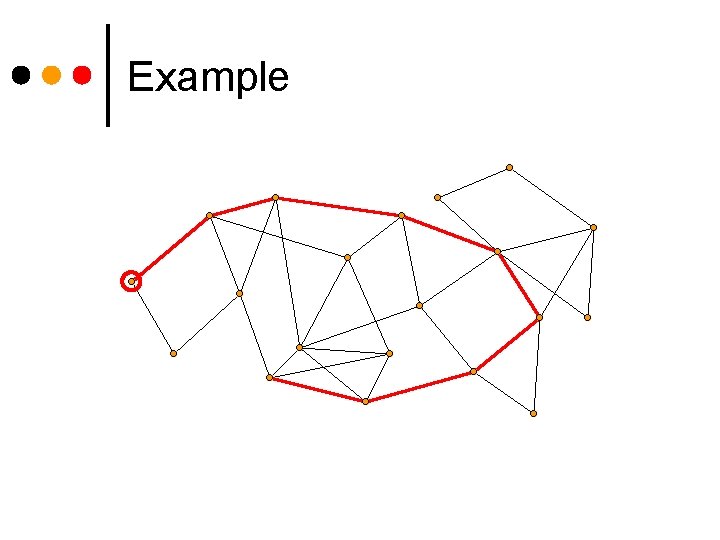
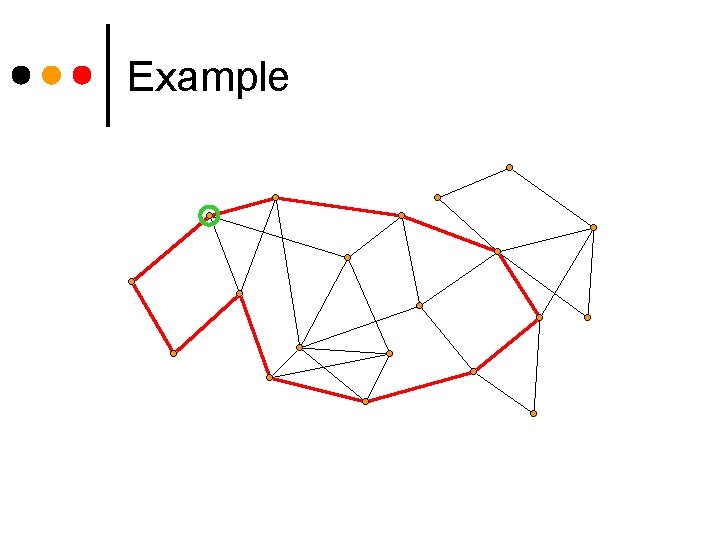
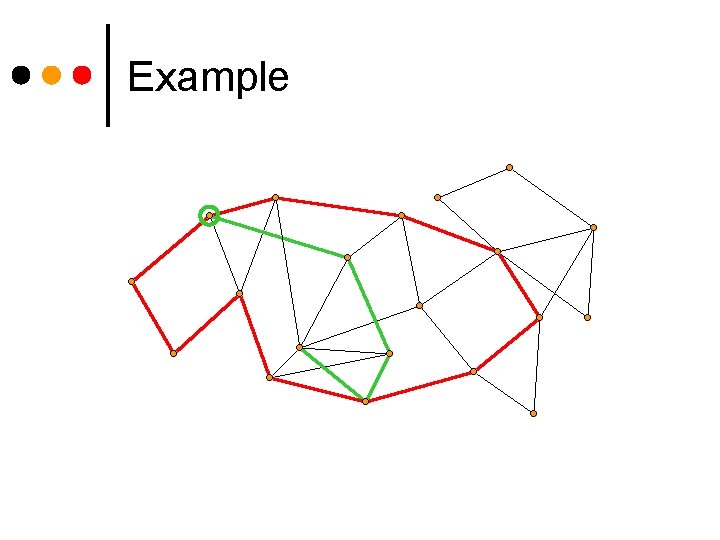
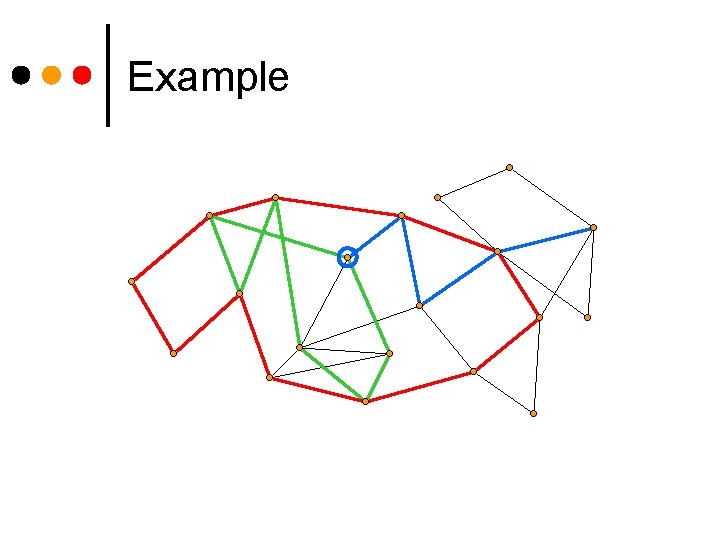
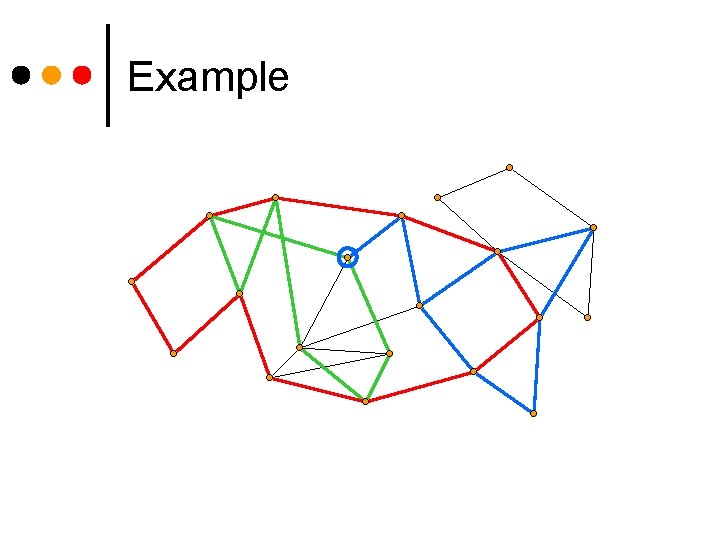
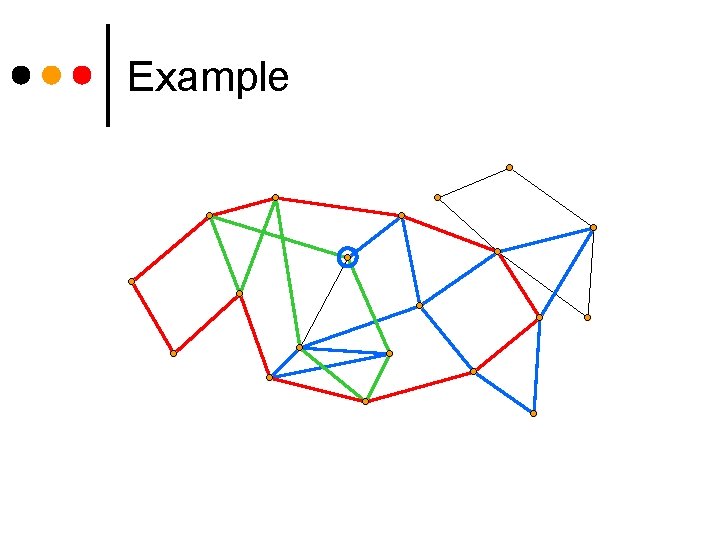
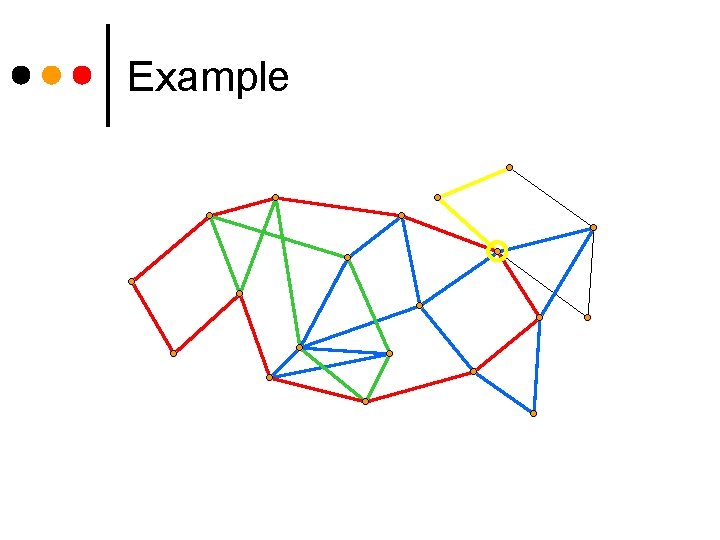
Example

Euler Paths Theorem: A graph G has an Euler path from v to w if G is connected, v and w have odd degree, and all other vertices have even degree. ¢ Proof: ¢ Add an edge from v to w. l Then the graph has an Euler circuit. l Remove the new edge from the circuit. l

Hamiltonian Circuits A Hamiltonian circuit is a simple circuit that includes every vertex of the graph. ¢ The Traveling Salesman Problem seeks a Hamiltonian circuit of minimal length. ¢

Hamiltonian Circuits ¢ Theorem: If a graph G has a nontrivial Hamiltonian circuit, then G has a subgraph H such that V(H) = V(G). l H is connected. l |E(H)| = |V(G)|. l deg(v) = 2 for all v V(H). l ¢ These conditions are necessary, but not sufficient.

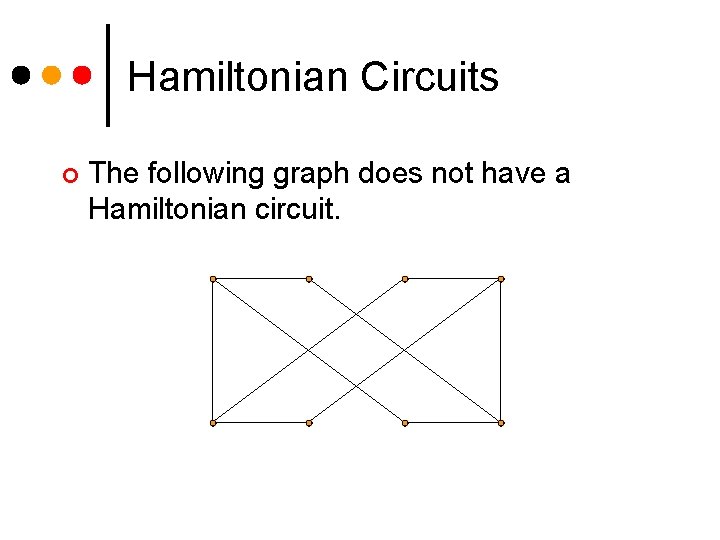
Hamiltonian Circuits ¢ The following graph does not have a Hamiltonian circuit.