Circuits Circuits We will build circuits for addition

Circuits

Circuits • We will build circuits for addition, multiplication and other arithmetic operations. • This is actually used! Everywhere!
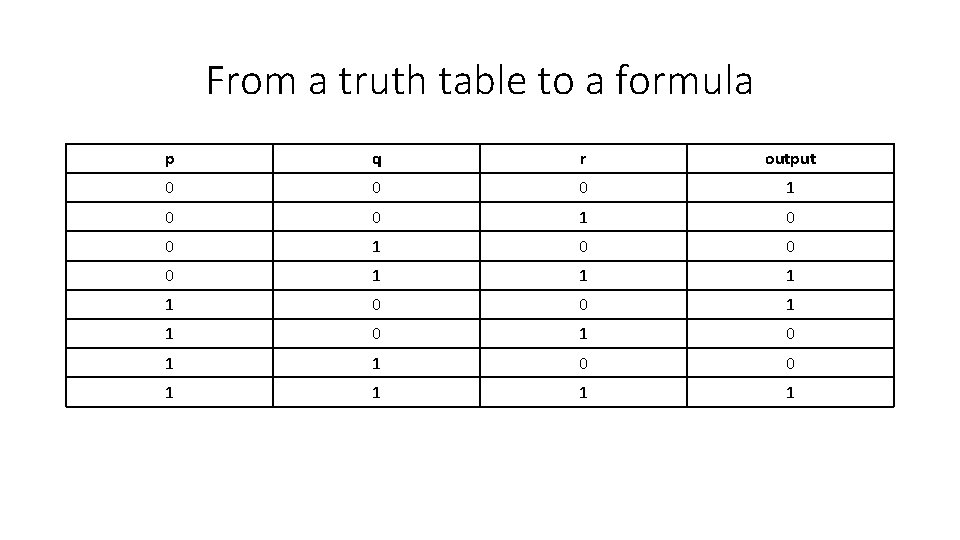
From a truth table to a formula p q r output 0 0 0 1 0 0 0 1 1 0 1 1 0 0 1 1

From a truth table to a formula p q r output 0 0 0 1 0 0 0 1 1 0 1 1 0 0 1 1 • Let us focus entirely on the rows that output 1!
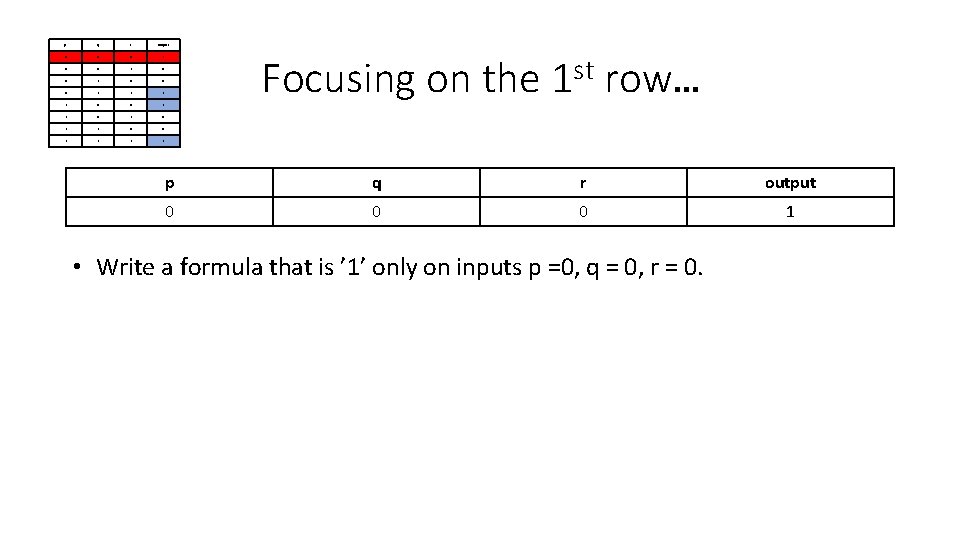
p q r output 0 0 0 1 0 0 0 1 1 0 1 1 0 0 1 1 Focusing on the st 1 row… p q r output 0 0 0 1 • Write a formula that is ’ 1’ only on inputs p =0, q = 0, r = 0.

p q r output 0 0 0 1 0 0 0 1 1 0 1 1 0 0 1 1 Focusing on the st 1 row… p q r output 0 0 0 1
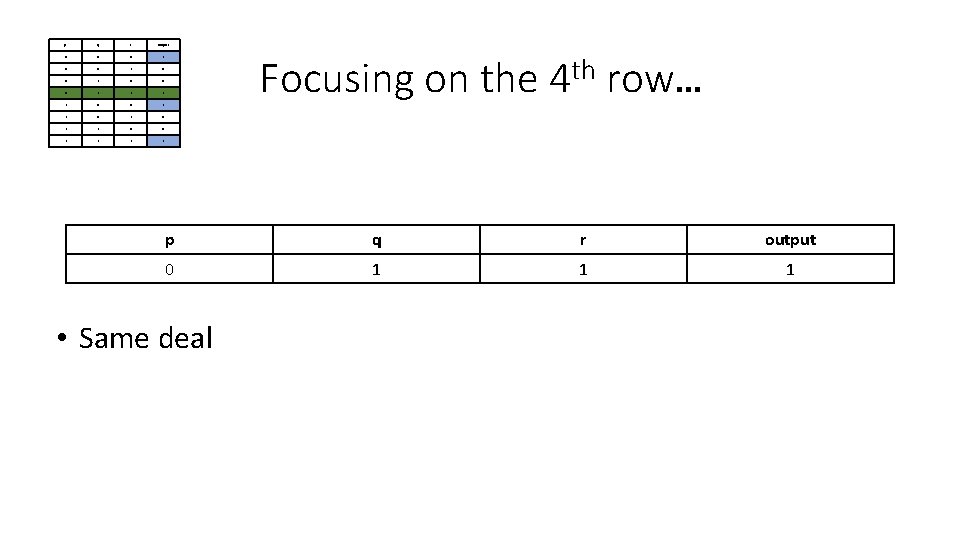
p q r output 0 0 0 1 0 0 0 1 1 0 1 1 0 0 1 1 Focusing on the th 4 row… p q r output 0 1 1 1 • Same deal
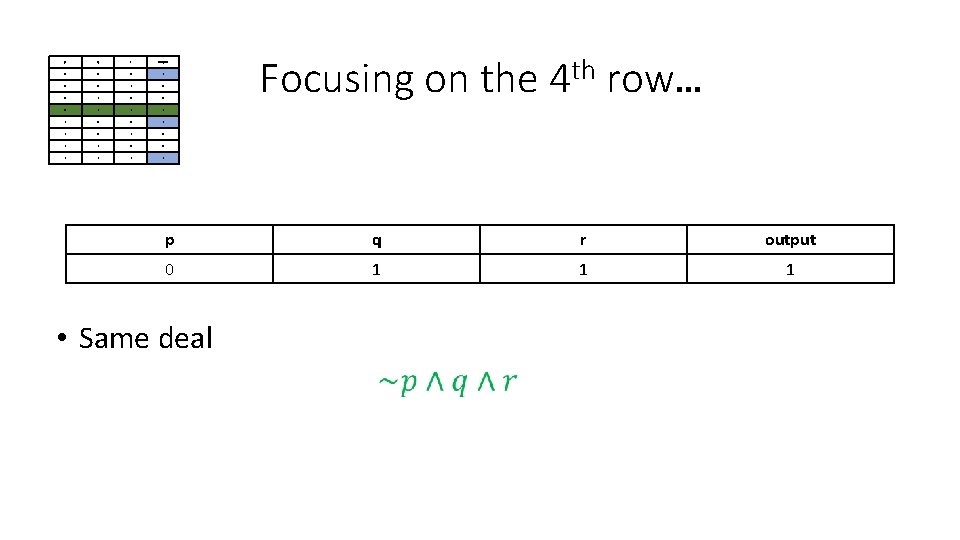
p q r output 0 0 0 1 0 0 0 1 1 0 1 1 0 0 1 1 Focusing on the th 4 row… p q r output 0 1 1 1 • Same deal
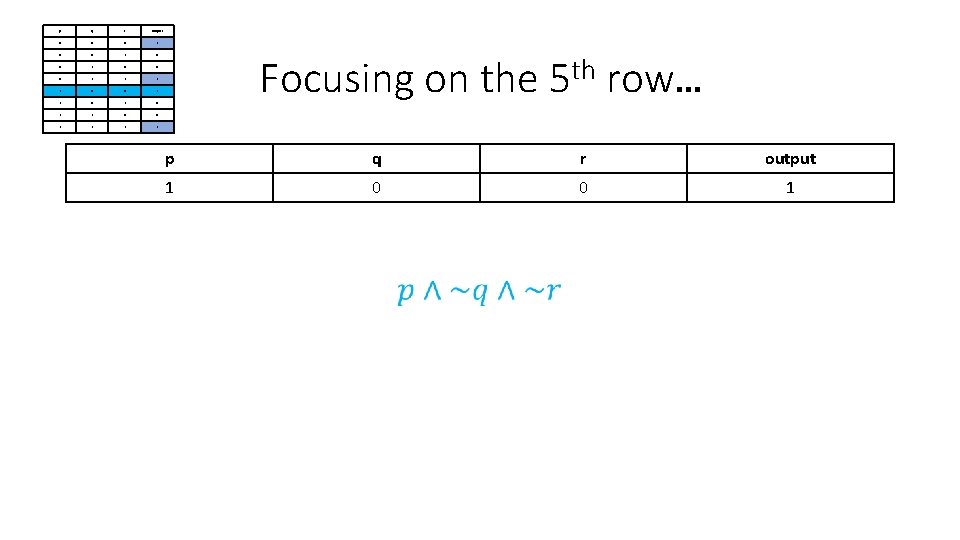
p q r output 0 0 0 1 0 0 0 1 1 0 1 1 0 0 1 1 Focusing on the th 5 row… p q r output 1 0 0 1
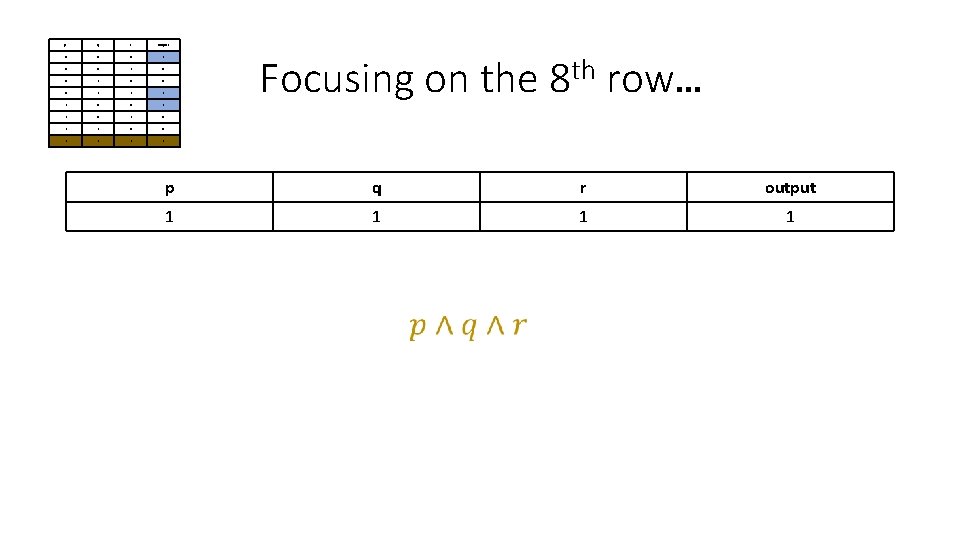
p q r output 0 0 0 1 0 0 0 1 1 0 1 1 0 0 1 1 Focusing on the th 8 row… p q r output 1 1

How do we combine those simple formulae?

How do we combine those simple formulae? p q r output 0 0 0 1 0 0 0 1 1 0 1 1 0 0 1 1 • Outputs 1 if and only if the truth table outputs 1!

How do we combine those simple formulae? p q r output 0 0 0 1 0 0 0 1 1 0 1 1 0 0 1 1 • Outputs 1 if and only if the truth table outputs 1! • We want to do this in hardware!

Logical gates • The smallest pieces of hardware that we will examine are called logical gates. • Every gate that we encounter will take bits as inputs and will emit one bit as output. Gate • Those gates can connect to each other in various different ways in order to create more complex circuits

Our first gate 0 1 1 0 • This gate is known as the inverter. • It corresponds exactly to the negation operation in propositional logic! • Where 1, set True. • Where 0, set False

Our second gate 0 0 1 1 1 • Corresponds to: Conjunction Disjunction

Our second gate (AND gate) 0 0 1 1 1 • Corresponds to: Conjunction Disjunction

Our third gate (OR gate) • Corresponds to logical disjunction (OR) 0 0 1 1 1 0 1 1
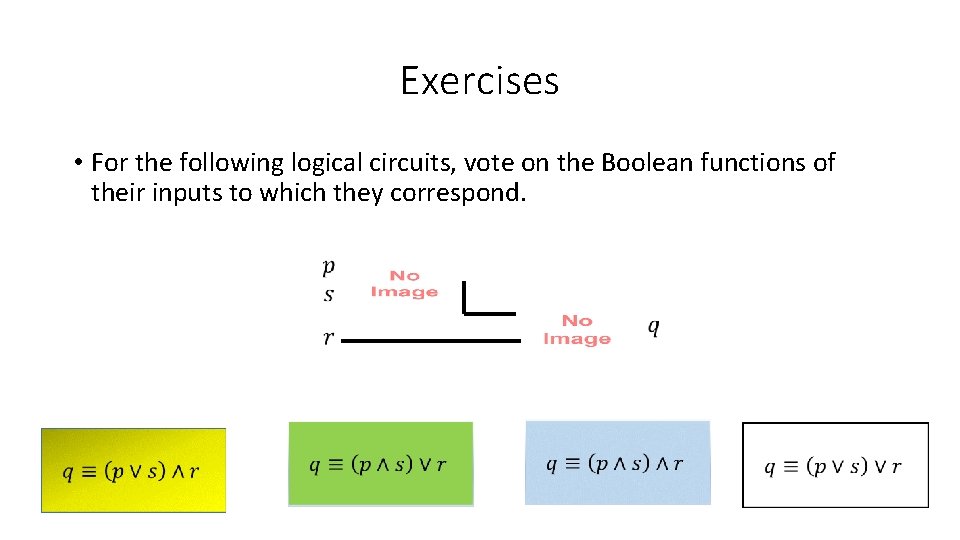
Exercises • For the following logical circuits, vote on the Boolean functions of their inputs to which they correspond.
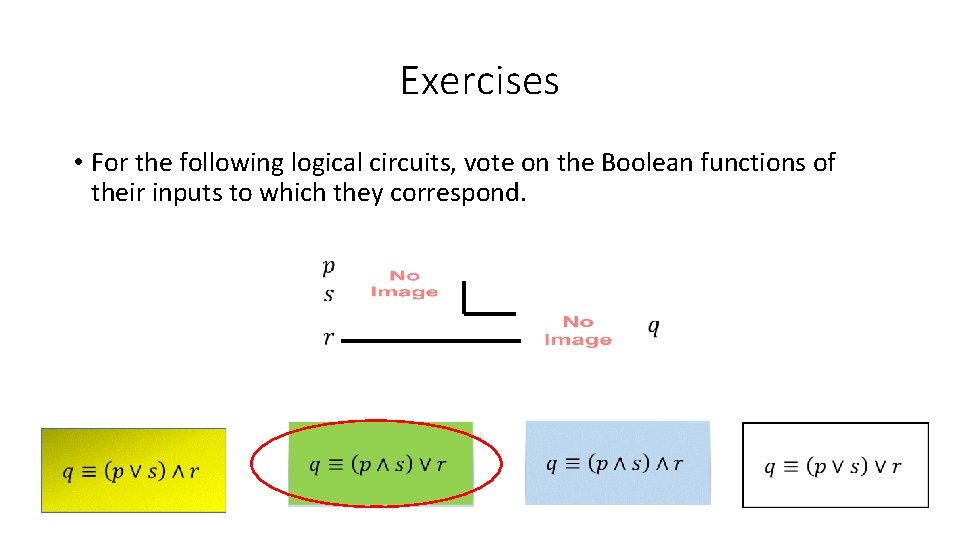
Exercises • For the following logical circuits, vote on the Boolean functions of their inputs to which they correspond.
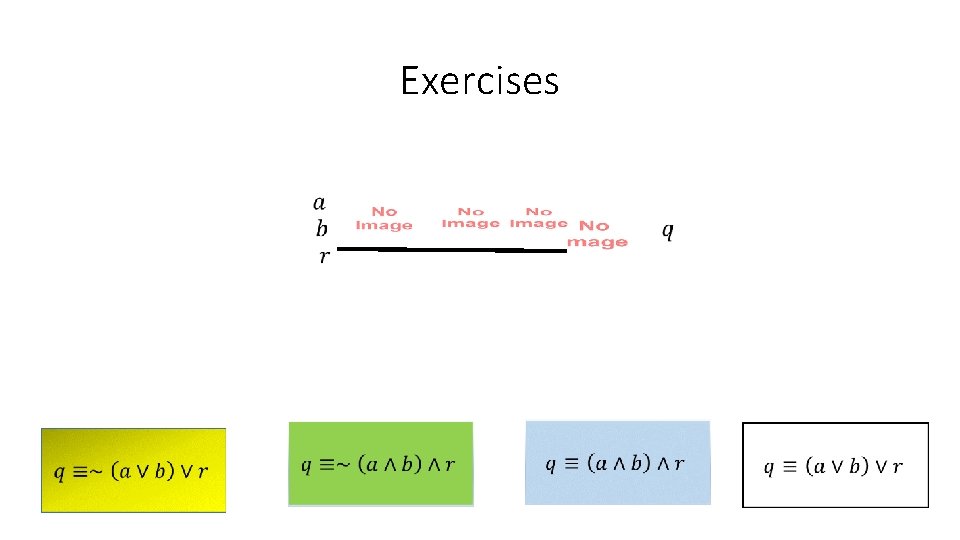
Exercises
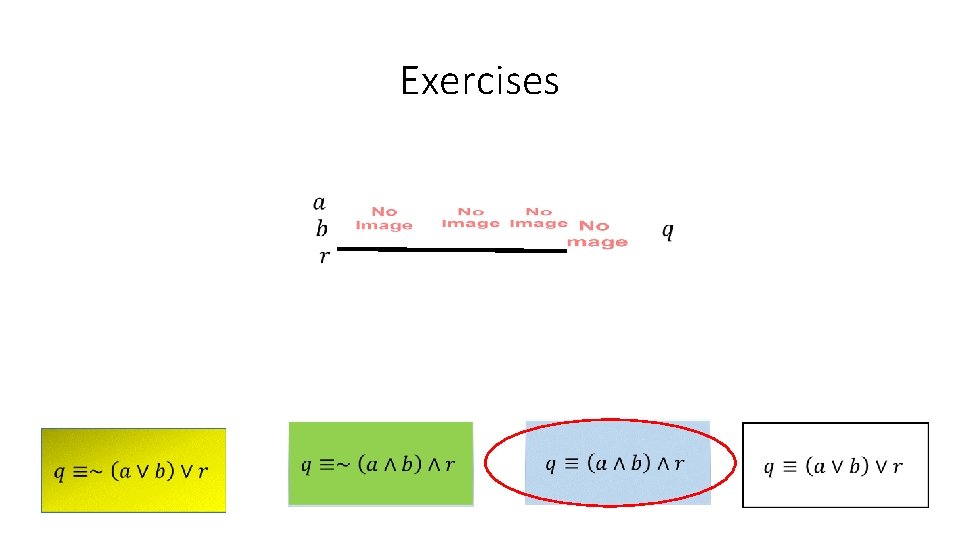
Exercises
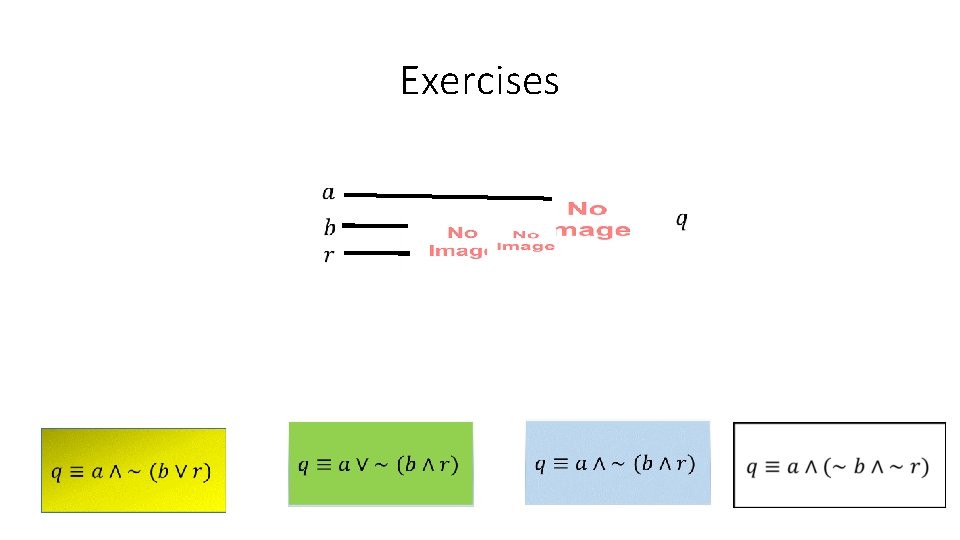
Exercises
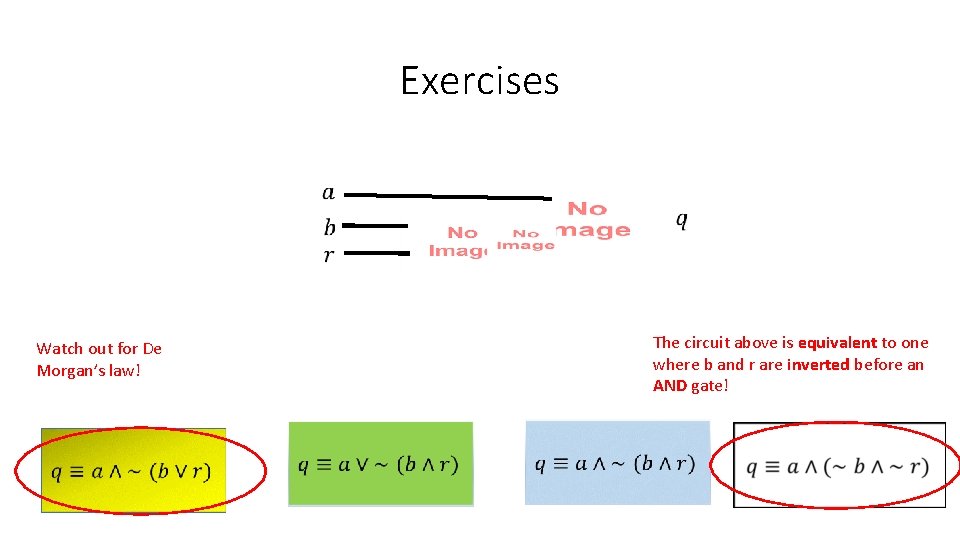
Exercises The circuit above is equivalent to one where b and r are inverted before an AND gate! Watch out for De Morgan’s law!

Coming back to our original truth table…

Coming back to our original truth table… • For each small formula we have a circuit, and we will combine with a 4 -input OR gate!
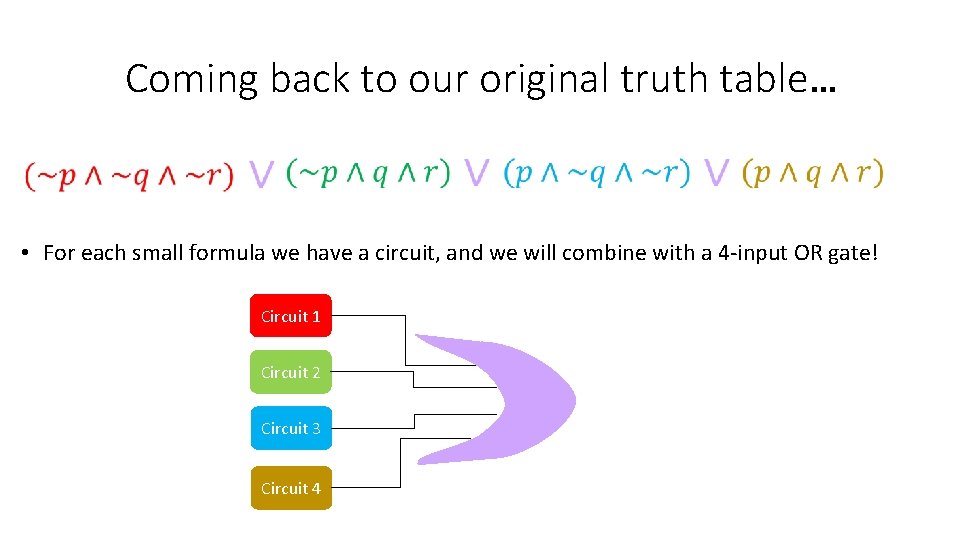
Coming back to our original truth table… • For each small formula we have a circuit, and we will combine with a 4 -input OR gate! Circuit 1 Circuit 2 Circuit 3 Circuit 4
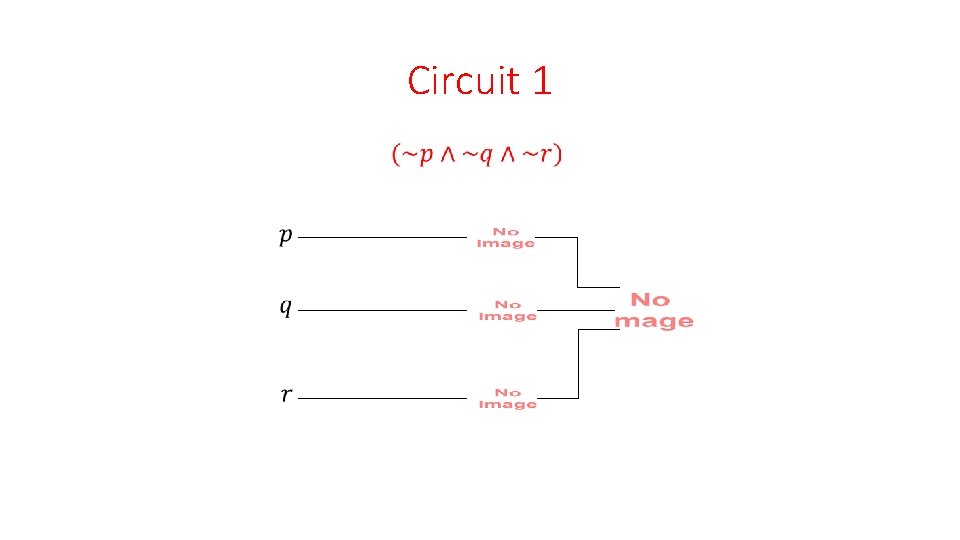
Circuit 1
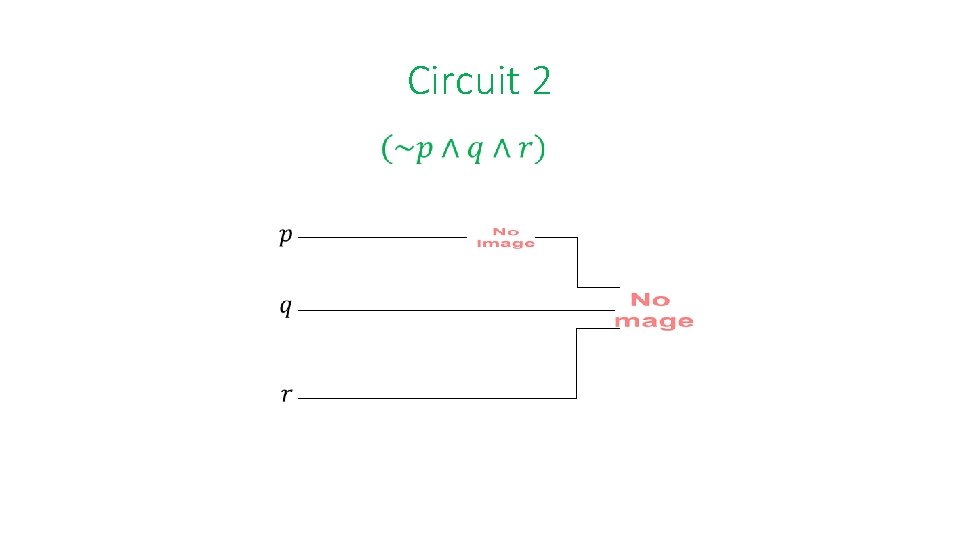
Circuit 2
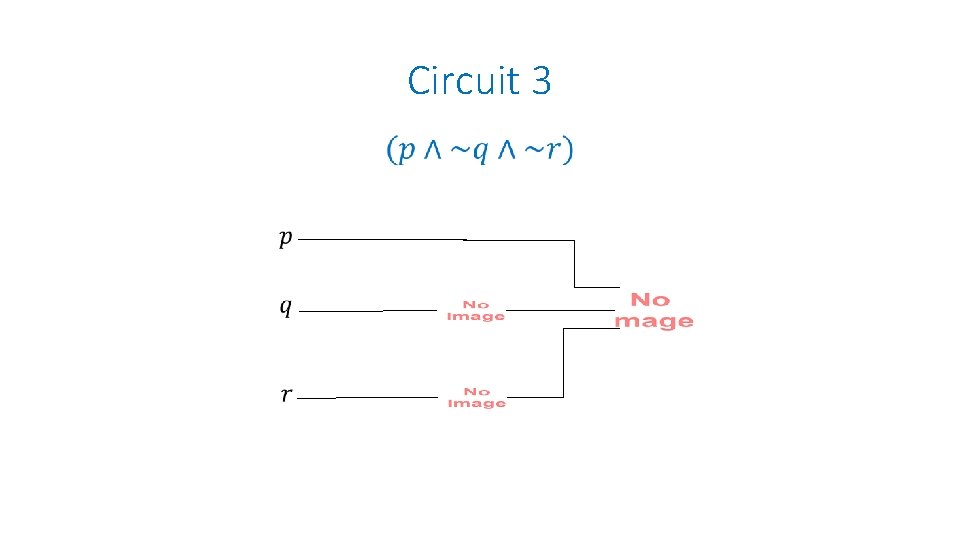
Circuit 3
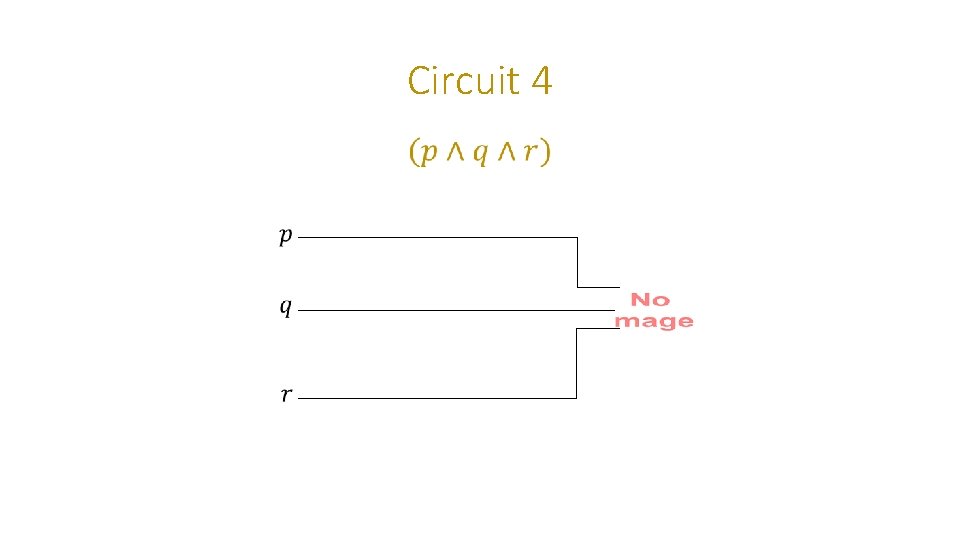
Circuit 4

Building Adder Circuits • We want to build circuits that add arbitrarily large binary numbers. • E. g 1001 Inputs +0011 Output 1100

Half-Adder •
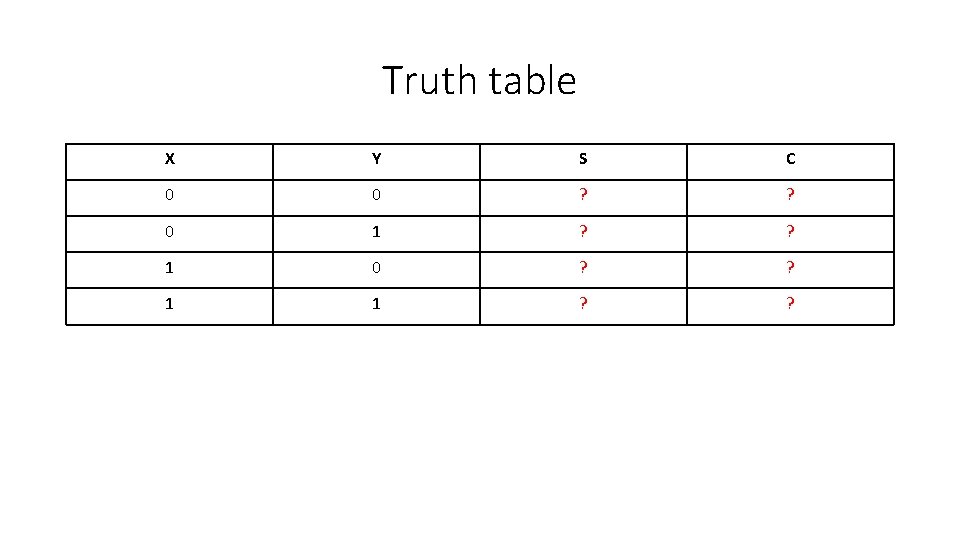
Truth table X Y S C 0 0 ? ? 0 1 ? ? 1 0 ? ? 1 1 ? ?
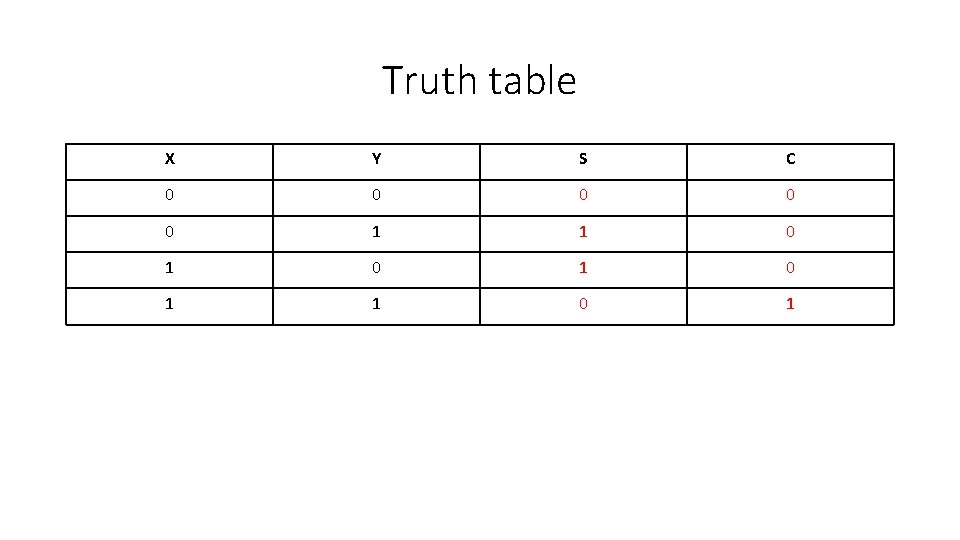
Truth table X Y S C 0 0 0 1 1 0 1 0 1
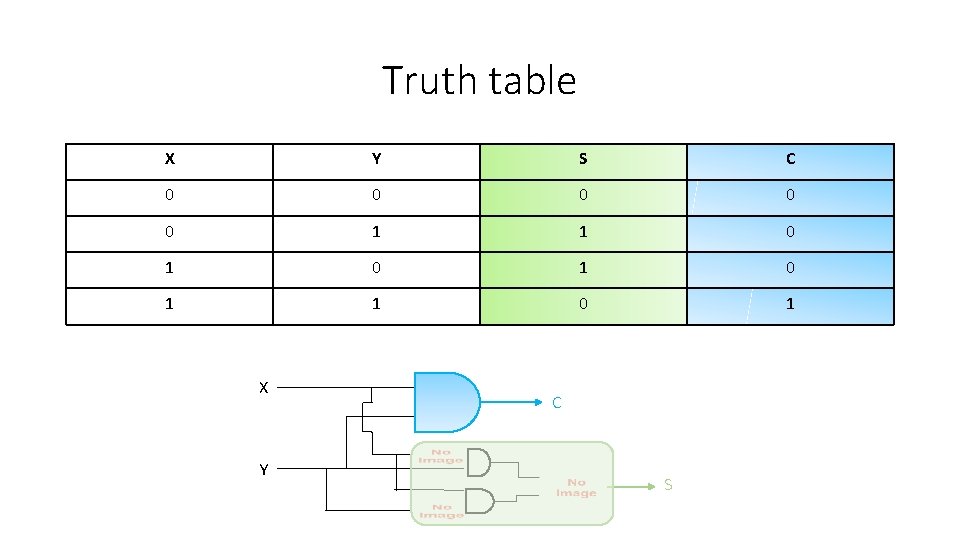
Truth table X Y S C 0 0 0 1 1 0 1 0 1 X Y C S
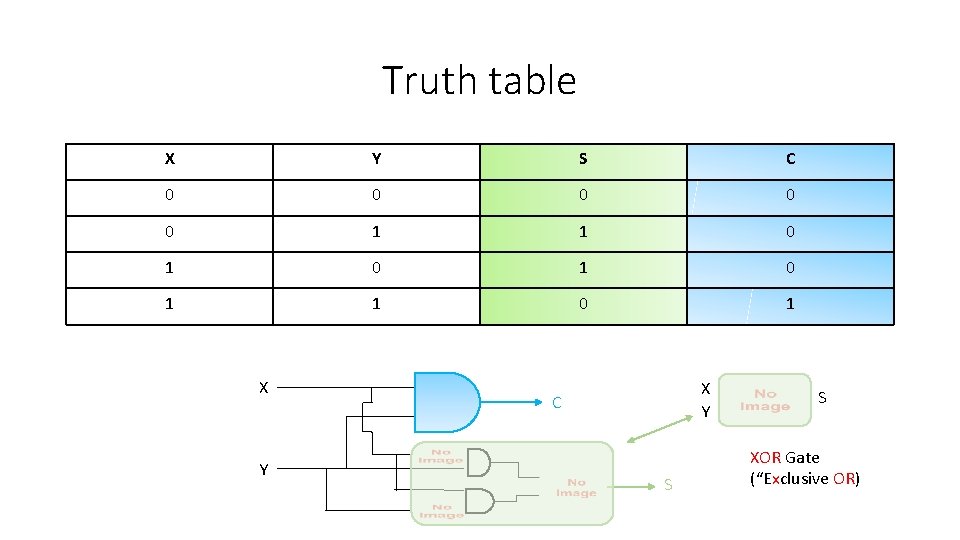
Truth table X Y S C 0 0 0 1 1 0 1 0 1 X Y C S S XOR Gate (“Exclusive OR)
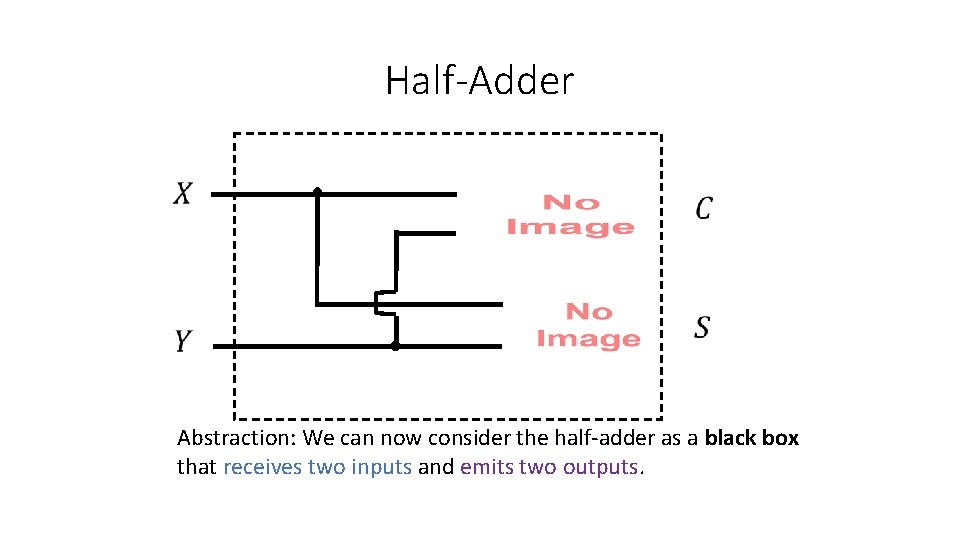
Half-Adder Abstraction: We can now consider the half-adder as a black box that receives two inputs and emits two outputs.
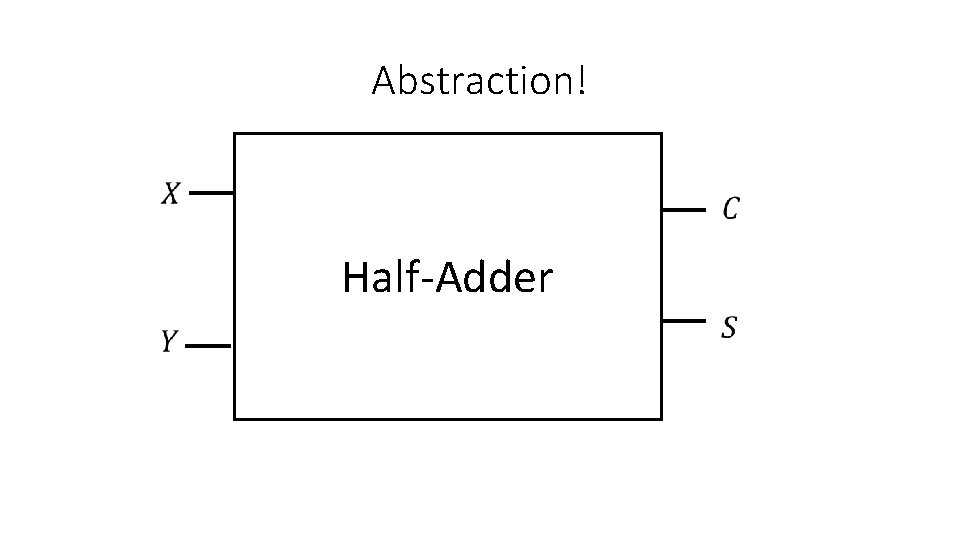
Abstraction! Half-Adder

Full-Adder • Now, let’s consider the complete case, where we want to build a circuit that computes the sum of two 2 -digit binary numbers: P Q + W X C S 1 S 2 • To do this, we also need the ability to add 3 digits, because: C 1 P Q + W X C S 1 S 2

Full-Adder • Now, let’s consider the complete case, where we want to build a circuit that computes the sum of two 2 -digit binary numbers: P Q + W X C S 1 S 2 • To do this, we also need the ability to add 3 digits, because: C 1 We will call a circuit P Q that adds 3 digits a full adder + W X C S 1 S 2
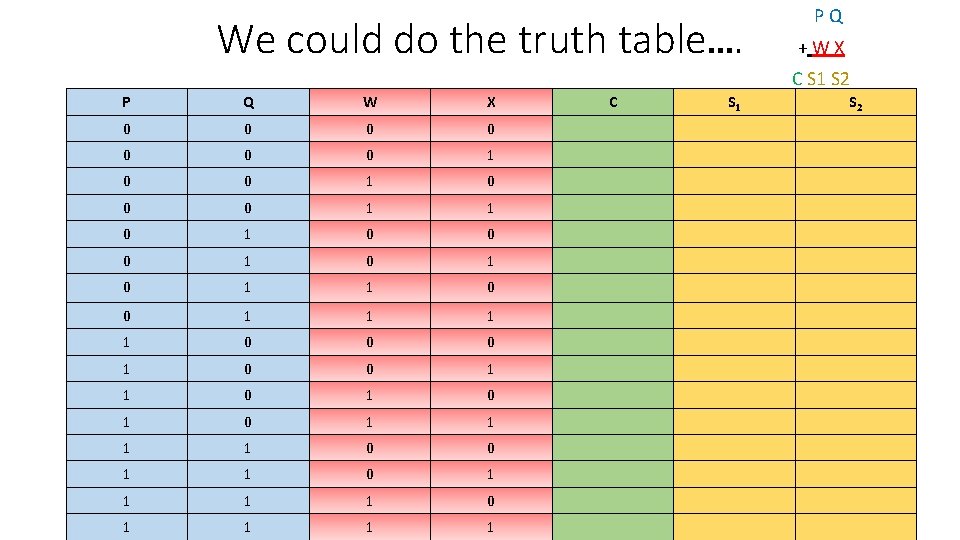
We could do the truth table…. P Q + W X C S 1 S 2 P Q W X 0 0 0 0 1 1 0 0 0 1 0 1 1 0 0 0 1 1 0 1 0 1 1 0 0 1 1 1 1 0 1 1 C S 1 S 2
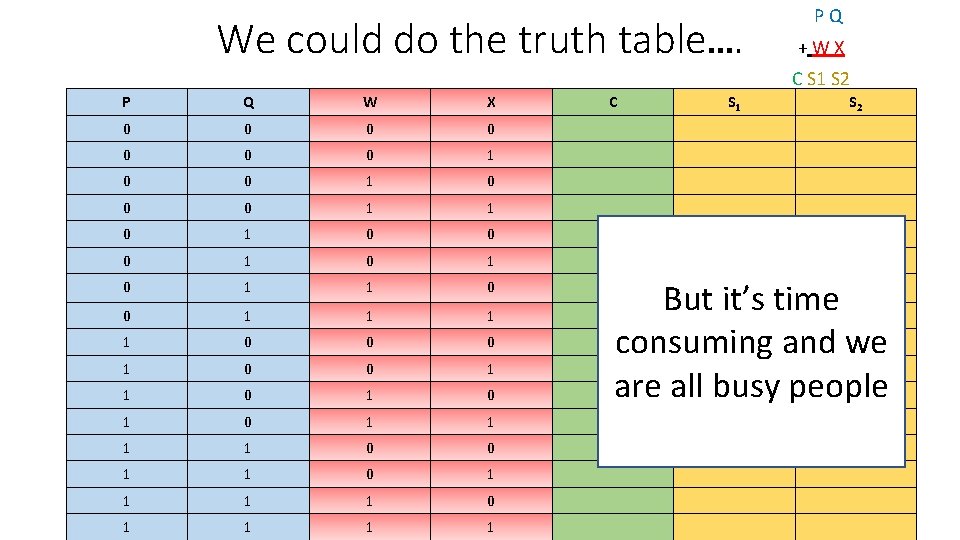
We could do the truth table…. P Q + W X C S 1 S 2 P Q W X 0 0 0 0 1 1 0 0 0 1 0 1 1 0 0 0 1 1 0 1 0 1 1 0 0 1 1 1 1 0 1 1 C S 1 S 2 But it’s time consuming and we are all busy people
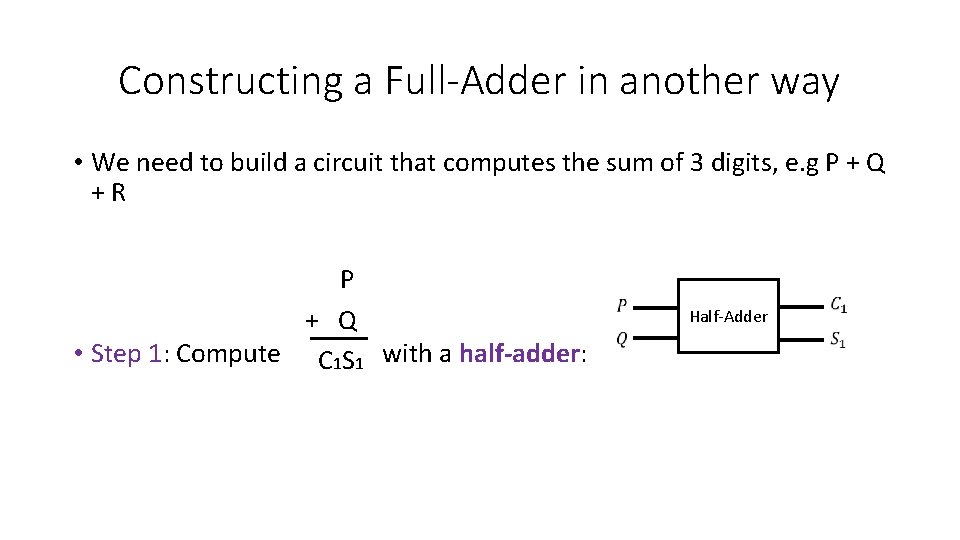
Constructing a Full-Adder in another way • We need to build a circuit that computes the sum of 3 digits, e. g P + Q + R P + Q • Step 1: Compute with a half-adder: C 1 S 1 Half-Adder
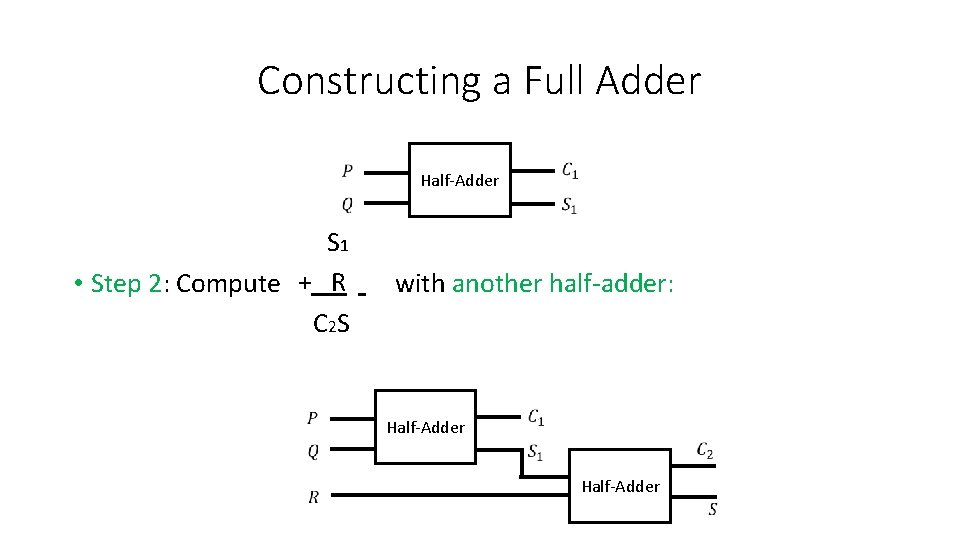
Constructing a Full Adder Half-Adder S 1 + R • Step 2: Compute with another half-adder: C 2 S Half-Adder
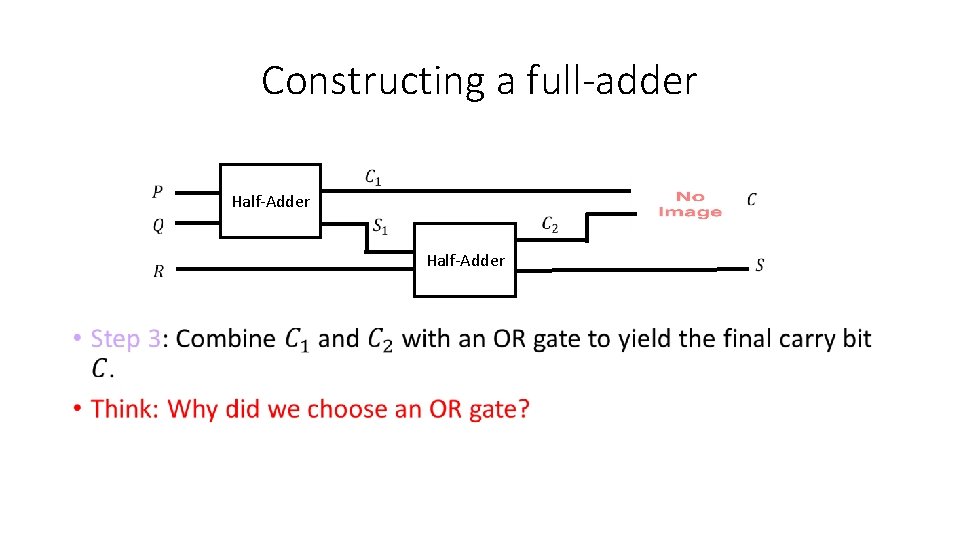
Constructing a full-adder • Half-Adder
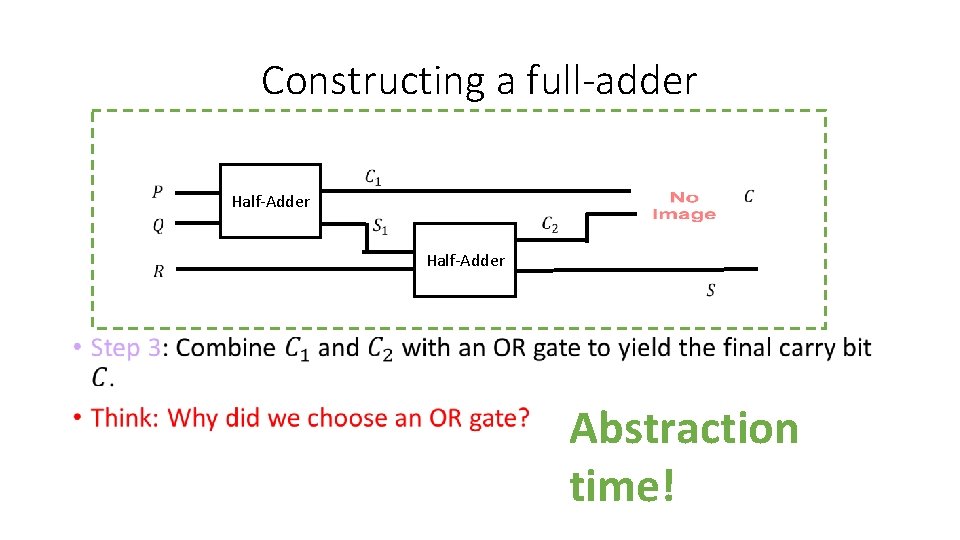
Constructing a full-adder Half-Adder • Abstraction time!
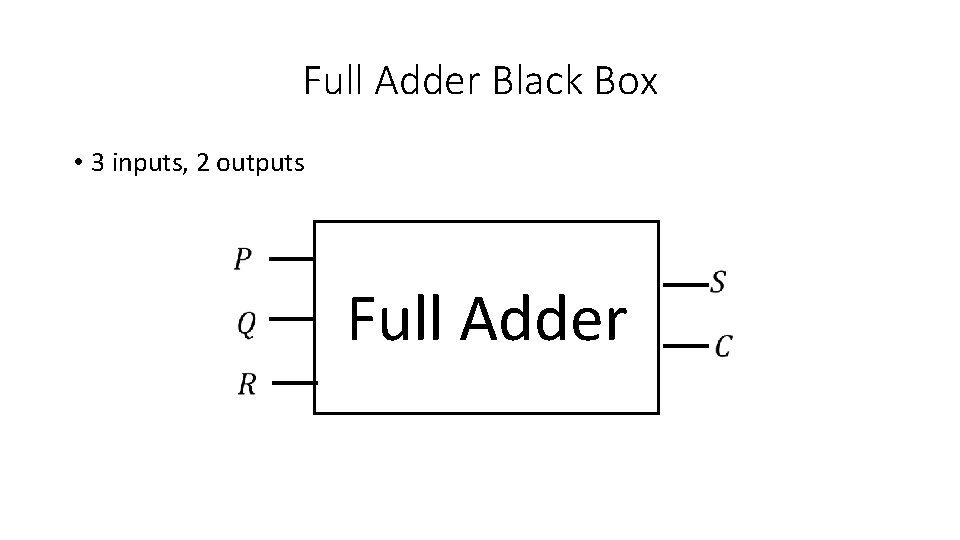
Full Adder Black Box • 3 inputs, 2 outputs Full Adder
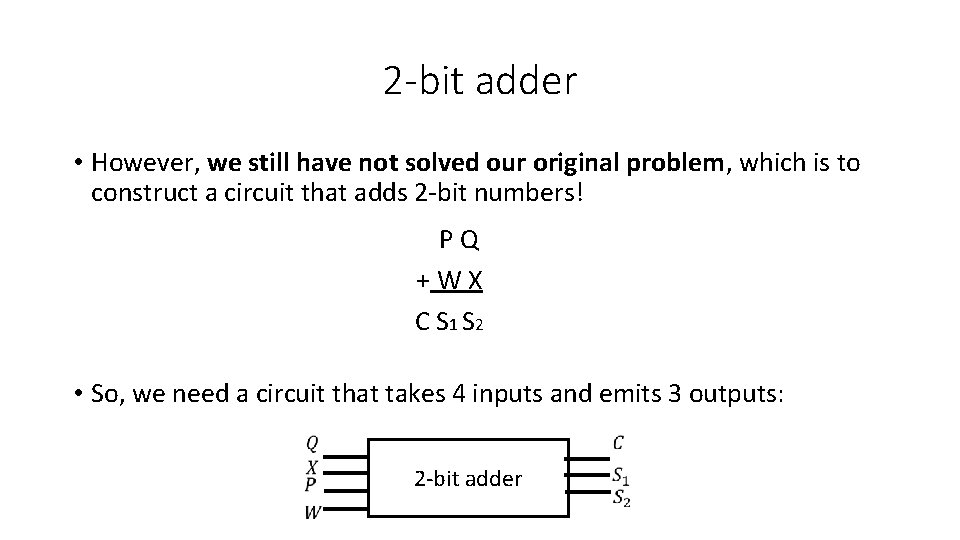
2 -bit adder • However, we still have not solved our original problem, which is to construct a circuit that adds 2 -bit numbers! P Q + W X C S 1 S 2 • So, we need a circuit that takes 4 inputs and emits 3 outputs: 2 -bit adder
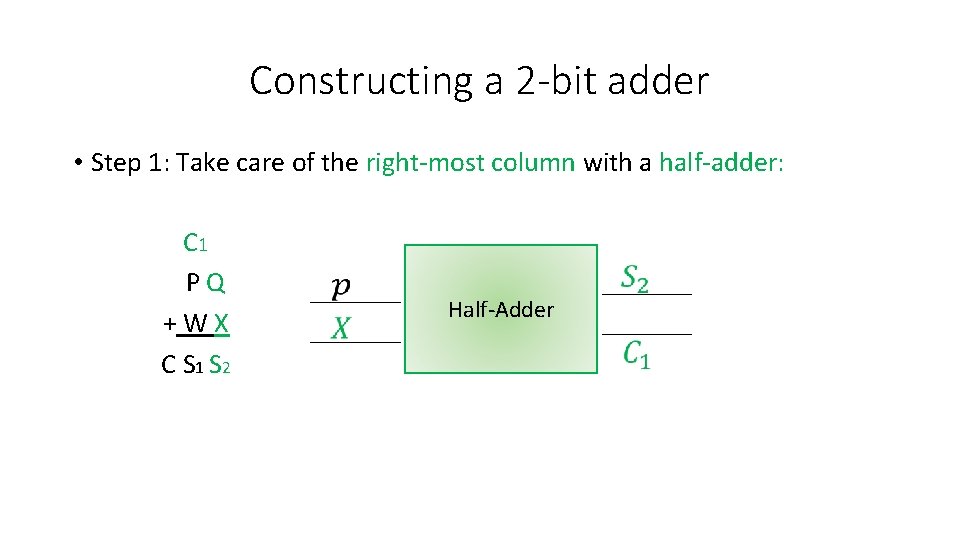
Constructing a 2 -bit adder • Step 1: Take care of the right-most column with a half-adder: C 1 P Q + W X C S 1 S 2 Half-Adder
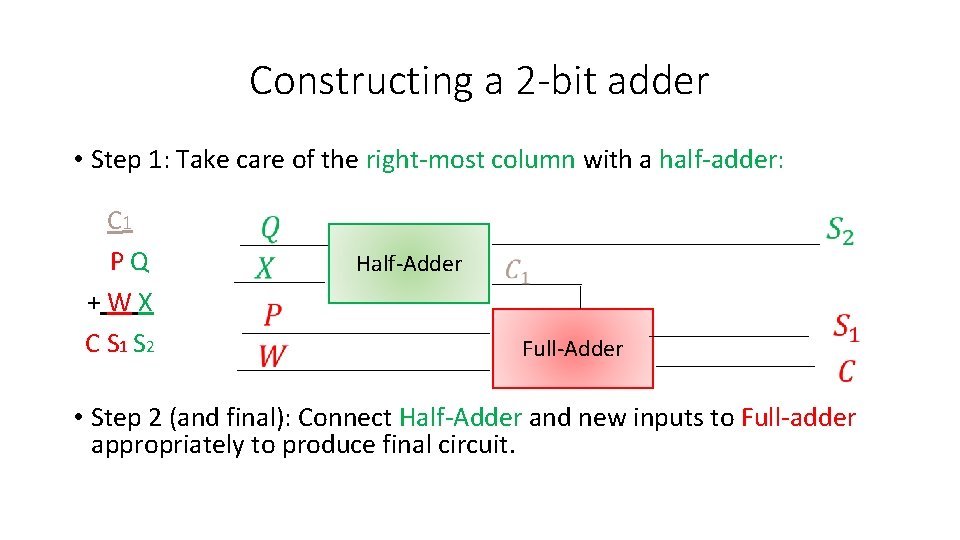
Constructing a 2 -bit adder • Step 1: Take care of the right-most column with a half-adder: C 1 P Q + W X C S 1 S 2 Half-Adder Full-Adder • Step 2 (and final): Connect Half-Adder and new inputs to Full-adder appropriately to produce final circuit.
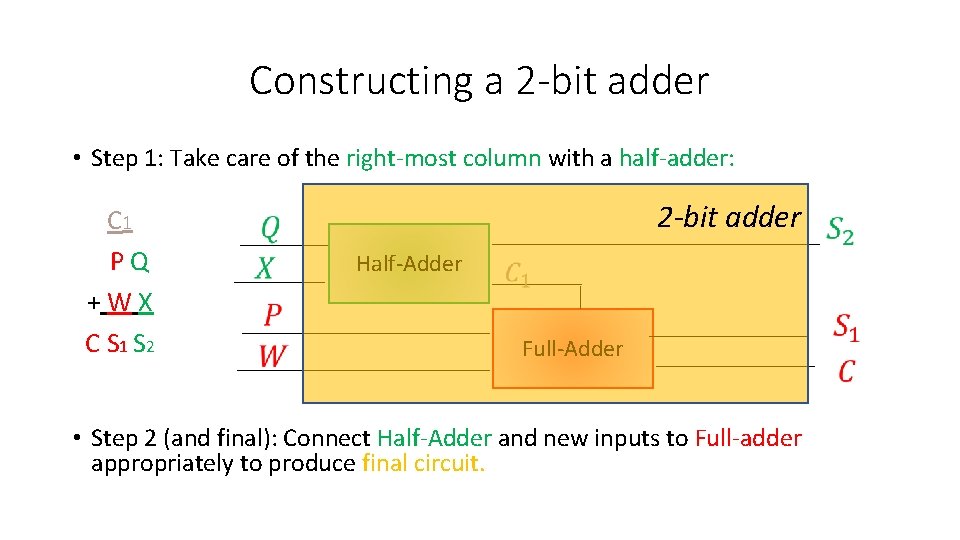
Constructing a 2 -bit adder • Step 1: Take care of the right-most column with a half-adder: C 1 P Q + W X C S 1 S 2 2 -bit adder Half-Adder Full-Adder • Step 2 (and final): Connect Half-Adder and new inputs to Full-adder appropriately to produce final circuit.
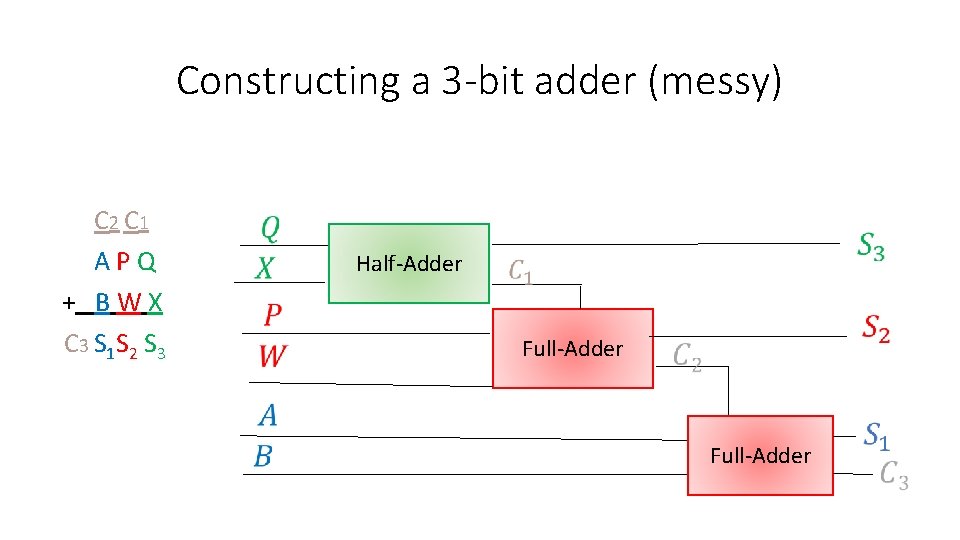
Constructing a 3 -bit adder (messy) C 2 C 1 A P Q + B W X C 3 S 1 S 2 S 3 Half-Adder Full-Adder
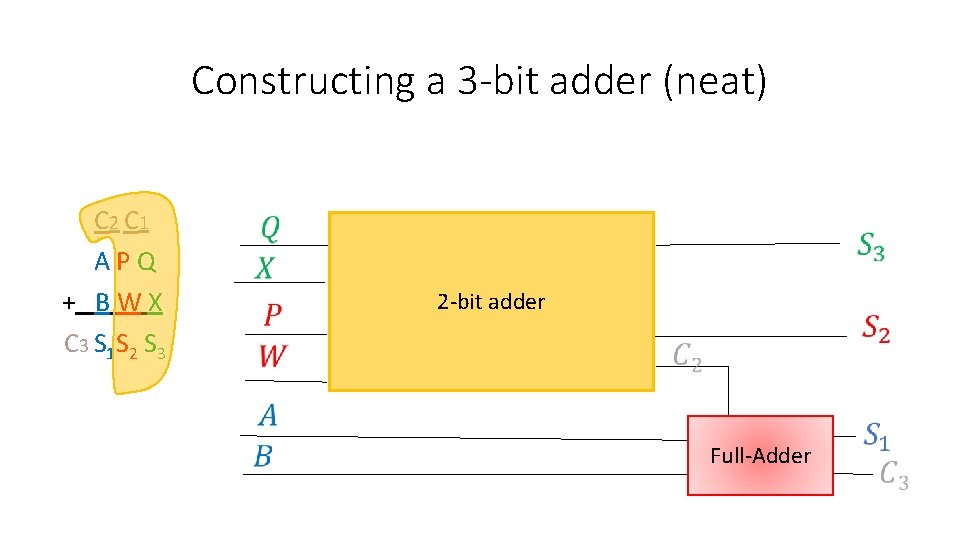
Constructing a 3 -bit adder (neat) C 2 C 1 A P Q + B W X C 3 S 1 S 2 S 3 2 -bit adder Full-Adder
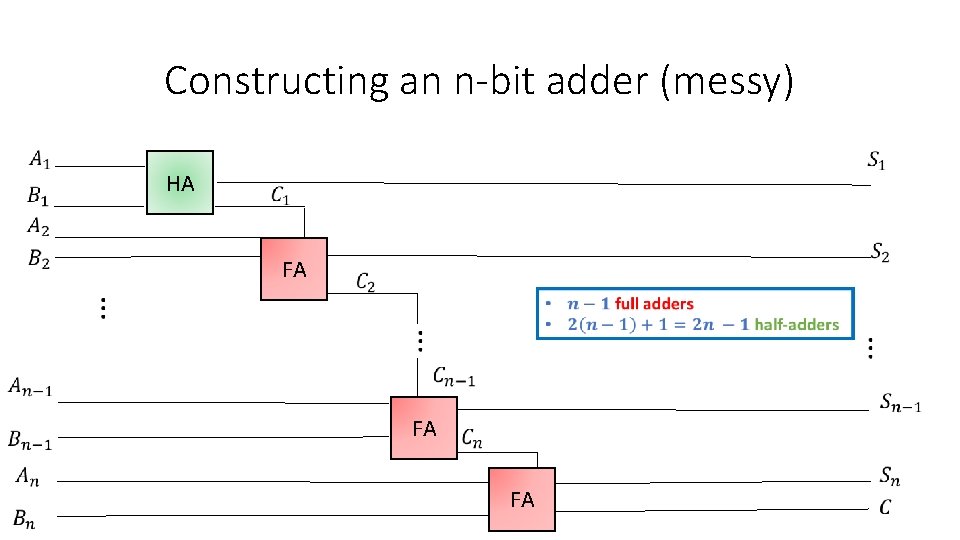
Constructing an n-bit adder (messy) HA FA FA
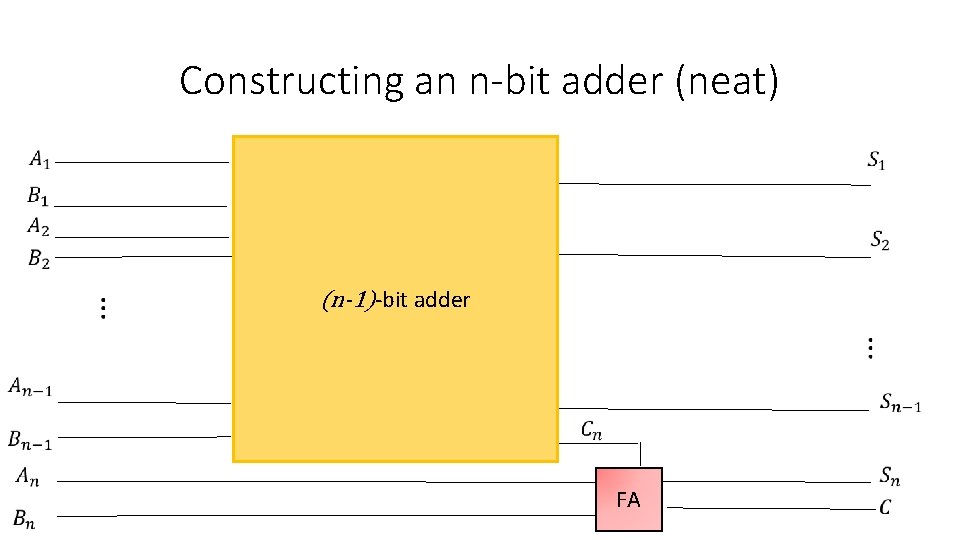
Constructing an n-bit adder (neat) (n-1)-bit adder FA

Other numeric functions • Addition (have done) • Multiplication • Division • Primality test (test whether a number is prime) • There are circuits for all of these! • Computers actually work this way at the base level: they consist of gates.

Fun exercise • Input: number in binary • Output: number in unary (!) 0 0 0 1 1 1 1 Circuit
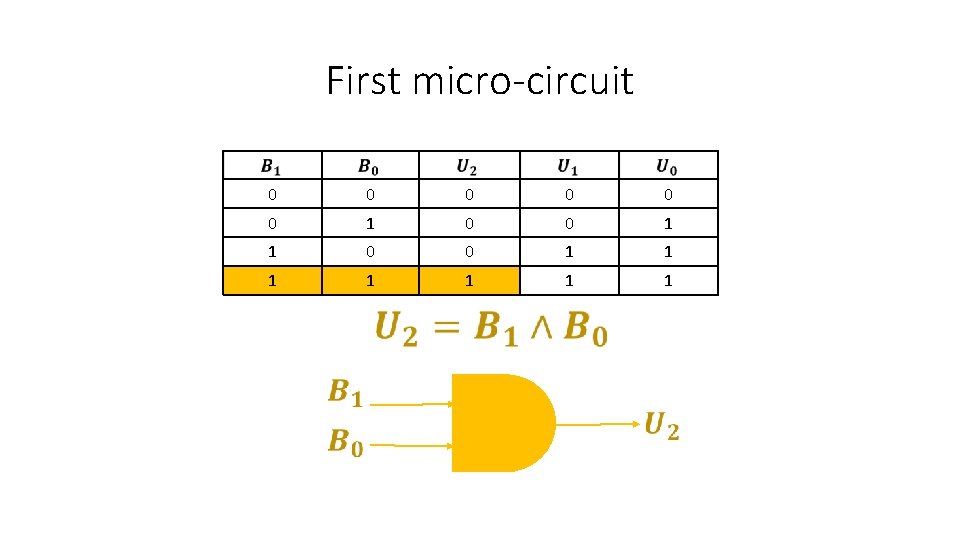
First micro-circuit 0 0 0 1 1 1 1
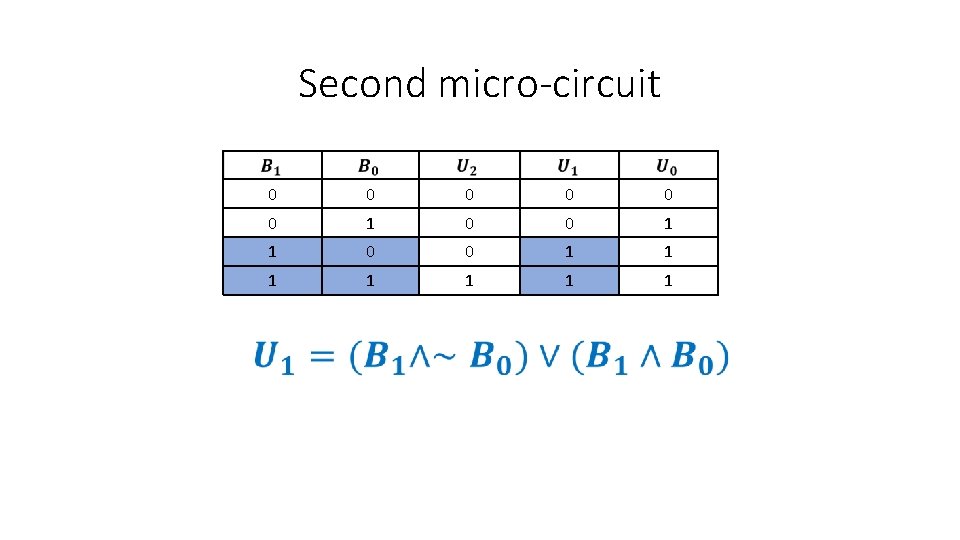
Second micro-circuit 0 0 0 1 1 1 1
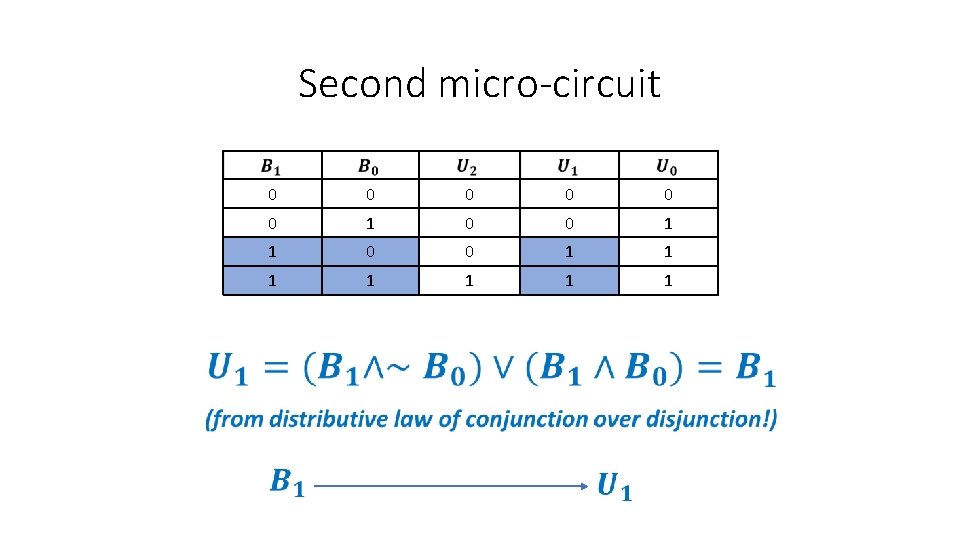
Second micro-circuit 0 0 0 1 1 1 1
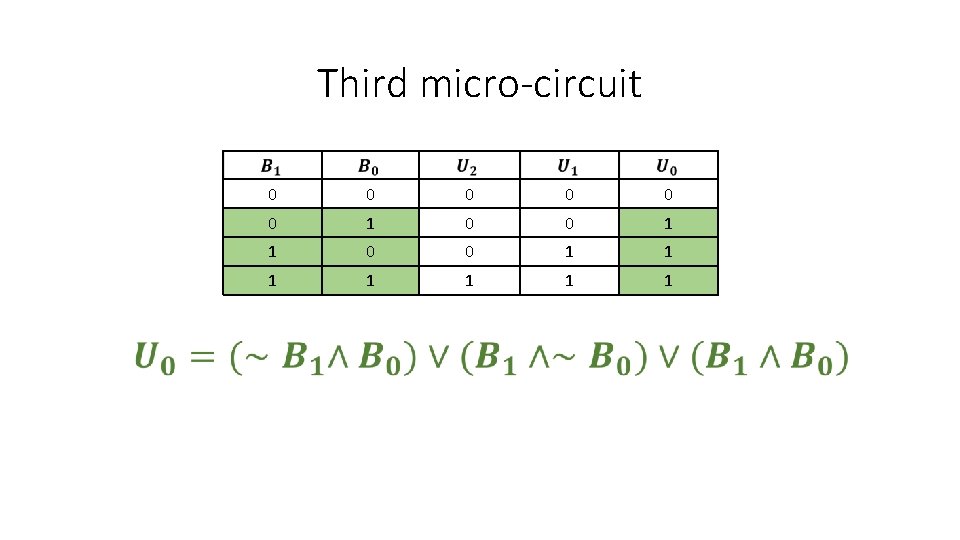
Third micro-circuit 0 0 0 1 1 1 1
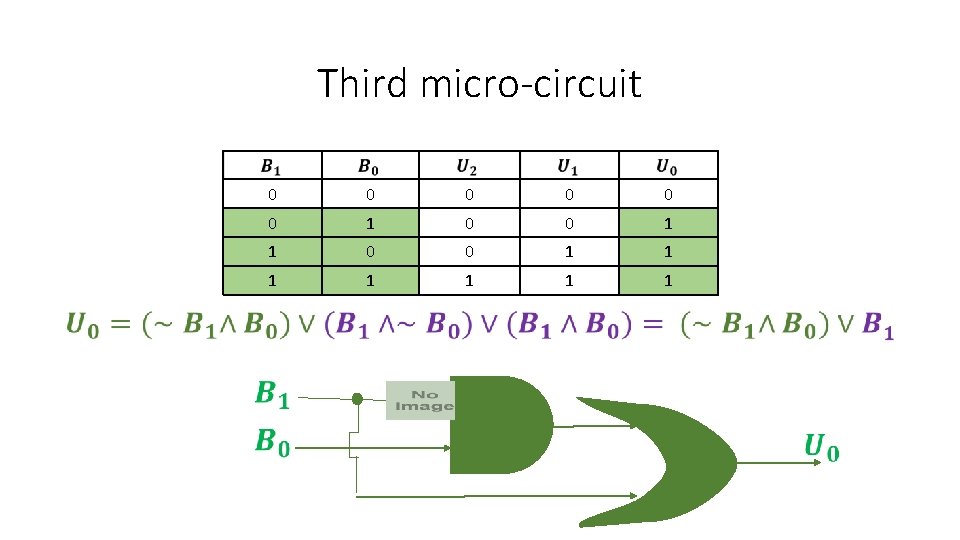
Third micro-circuit 0 0 0 1 1 1 1
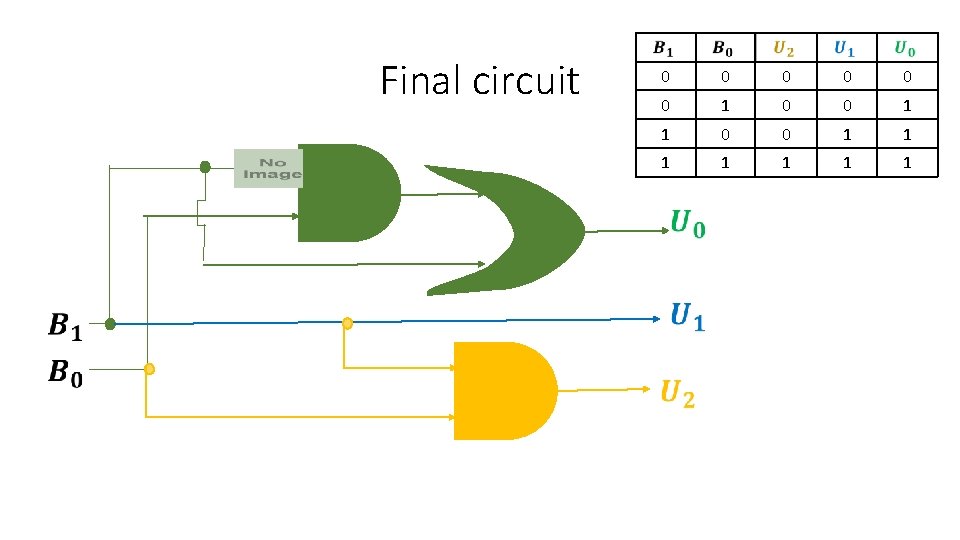
Final circuit 0 0 0 1 1 1 1
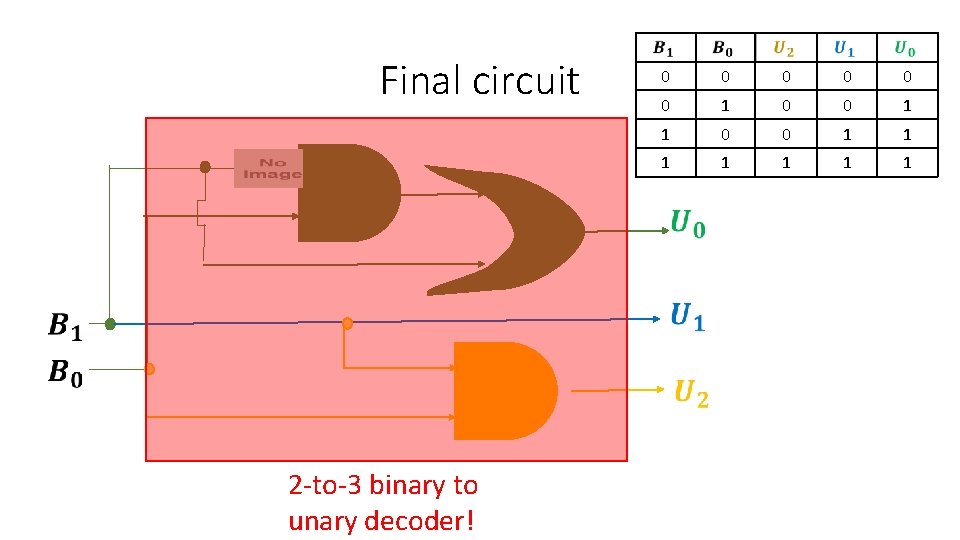
Final circuit 0 0 0 1 1 1 1 2 -to-3 binary to unary decoder!
- Slides: 65