Hamiltonian Systems Introduction Hamiltons Equations the Hamiltonian Phase

Hamiltonian Systems • • • Introduction Hamilton’s Equations & the Hamiltonian Phase Space Constants of the Motion & Integrable Hamiltonians Non-Integrable Systems, the KAM Theorem & Period. Doubling The Henon-Heiles Hamiltonian The Chirikov Standard Map The Arnold Cat Map The Dissipative Standard Map Applications

Introduction • No dissipation = Conservative – Phase space volume = constant – No transients, no attractors – Isolated (closed) system: Conservative • Open system: Dissipative • Hamiltonian system: Dynamics governed by H(q, p) – Solar system: • Gravitation: conservative • Tidal forces, solar wind: dissipative • Dissipation negligible for short times – Microscopic (quantum) systems • Integrable systems: non-chaotic

Hamilton’s Equations & the Hamiltonian • Hamilton formulation: phase space = { qi, pi } • Dynamics ( Hamilton’s equations ): Nf = degrees of freedom E. g. , n 3 -D particles: q = {qi} = { x 1, y 1, z 1, x 2, y 2, z 2, …, xn, yn, zn } p = {pi} = { px 1, py 1, pz 1, px 2, py 2, pz 2, …, pxn, pyn, pzn } Equivalent 1 st order system of ODEs ( “Do. F" = 2 Nf ): Nf = 3 n

Symplectic structure: manifold with a (symplectic) 2 -form as metric For the Hamiltonian systems: (Poisson bracket) Definition in terms of symplectic matrices ( see Goldstein ): ( M is symplectic if MT J M = J ) → H is conserved ( a constant of the motion ) if it’s not explicitly time dependent.

Phase Space For a conservative system, trajectories in phase space are confined to a constant energy surface. Do. F = N → energy surface is (2 N-1)-D Volume in state space of autonomous system See § 3. 13 For a conservative system H(q, p) : → no attractors → transients persist

Liouville’s Theorem Probability of finding a system in d. V = ρ= probability density of systems in phase space. = material / hydrodynamic derivative → Lagrangian picture = change of ρ at fixed phase point → Eulerian picture Liouville’s theorem: ~ no-crossing theorem for Hamiltonian systems

Integral Invariants is an integral invariant if I(t) is an integral invariant → where and Jik is the cofactor of Jik :

I(t) is an integral invariant → Liouville’s theorem: if ρ is the probability density of a Hamiltonian H(q, p, t). (ρ acts like an incompressible fluid ) Proof:

→ Alternatively: → & QED

In general: 1 st order ODEs: → Hamiltonian systems Equation is linear in ρ → • Evolution of ρ can’t be chaotic, even when individual trajectories are. • No “divergence” of evolution of nearby ρ’s. • No sensitivity to I. C. • Prototype of chaotic Hamiltonian system: Arnold cat map.

Constants of Motion & Integrable Hamiltonians Any quantity that is independent of t is a constant of the motion. For a conservative system, is independent of t. i. e t. , Ø Each point on a possible trajectory {q(t), p(t)} has the same energy E. Ø Many different trajectories may have the same energy. Ø E is a constant of the motion. Ø It is also an isolating integral that restricts the motion on some surface. Let pj be a constant of the motion, then i. e. , H is not explicitly dependent on qj. ( qj is cyclic ) Ø Each trajectory is confined to an (2 Nf-2)-D surface. Ø Each trajectory can be characterized by { E, pj 0 }.

k independent isolating integrals → each trajectory is confined to an (2 Nf-k)-D surface If k = Nf, the system is integrable. ( Trajectory Nf-D ) Isolating integrals are also called action variables Ji(q, p). The variable conjugate to Ji(q, p) is called an angle variable. Θi can always be chosen as dimensionless so that Ji has the dimension of action. { Θi, Ji } can be related to { q, p } by a canonical transformation. If H can be written as H(J), the system is integrable. i can be satisfied iff → System is in involution. i, j ( + independence )

Integrability can be examined by expressing the desired canonical transformations in terms of a Birkhoff series. Examples of integrable systems: • All 1 -D systems with analytic H → H = ωJ. • All systems with linear equations of motion → normal modes. • All systems that are completely separable. • Solitons Let H = H(J), then → Inverse transformation: For a bounded system, q and p must be periodic functions of Θ. Canonical perturbation theory: Series diverges → non-integrable q, p as series of Θ, J.

Simple Harmonic Oscillator → → Nf = 1 Phase space: 2 -D Trajectory: 1 -D ellipse) (H = const → Ellipses: periodic → Fixed point: = elliptic point Switching to (Θ, J): Trajectory is a circle of radius √J & area πJ in (P, Q) space Area of ellipse:

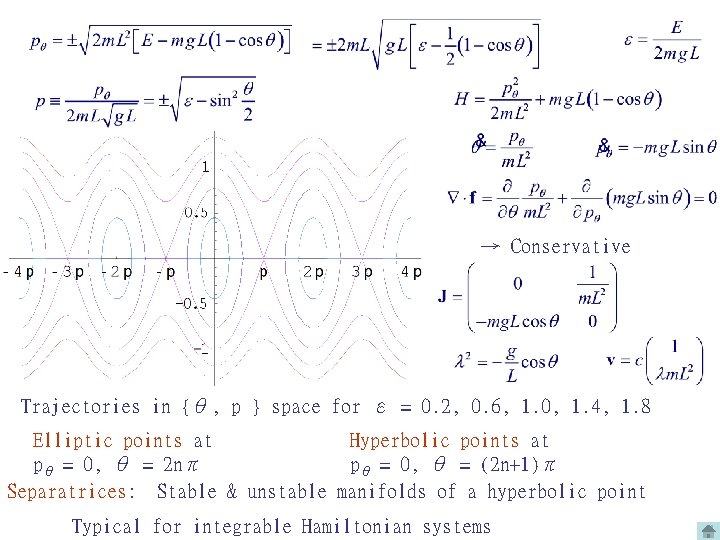
→ Conservative Trajectories in {θ, p } space for ε = 0. 2, 0. 6, 1. 0, 1. 4, 1. 8 Elliptic points at Hyperbolic points at pθ = 0, θ = 2 nπ pθ = 0, θ = (2 n+1)π Separatrices: Stable & unstable manifolds of a hyperbolic point Typical for integrable Hamiltonian systems

Elliptic Integrals & Elliptic Functions Ref: M. Abramowitz, I. A. Stegun, “Handbook od Mathematical Functions”. (Incomplete) Elliptic integrals: Complete Elliptic integrals: 1 st kind: 2 nd kind: (Jacobian) Elliptic functions: Mathematica: Elliptic. K[m] = Elliptic. F[π/2, m] Sin[φ] = Jacobi. SN[Elliptic. F[φ, m]

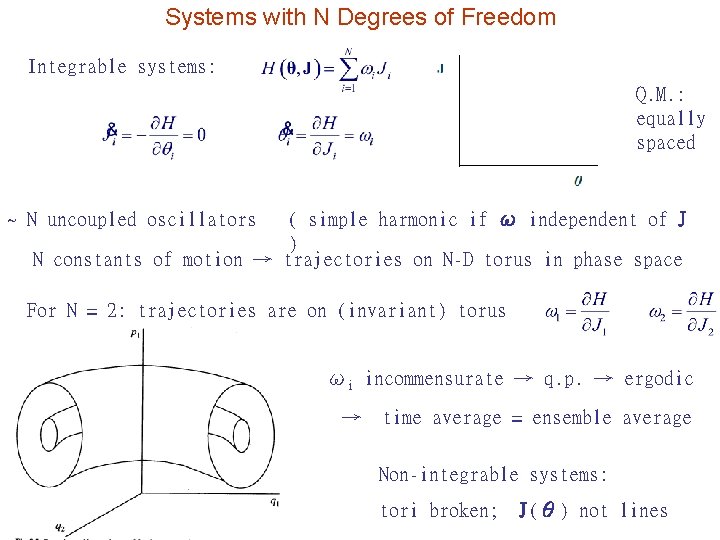
Systems with N Degrees of Freedom Integrable systems: Q. M. : equally spaced ~ N uncoupled oscillators ( simple harmonic if ω independent of J ) N constants of motion → trajectories on N-D torus in phase space For N = 2: trajectories are on (invariant) torus ωi incommensurate → q. p. → ergodic → time average = ensemble average Non-integrable systems: tori broken; J(θ) not lines

The Kepler Problem (Integrable) See H. Goldstein, "Classical Mechanics", 2 nd ed. , § 10 -7 ( with minor variations ) Solution of the (separable) Hamilton-Jacobi eq gives →

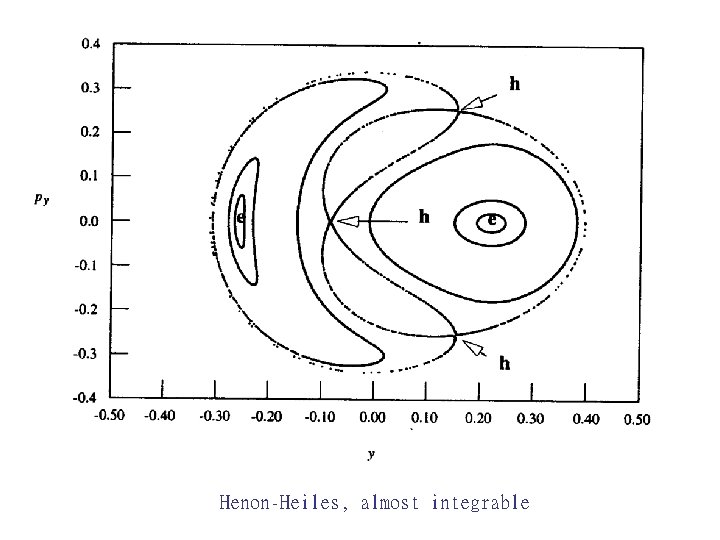
Nonintegrable Systems Integrable systems: periodic / q. p. Transition to chaos: → non-chaotic integrable → slightly non-integrable Non-integrable systems: Df 2 For Df = 2, integrable → motion on 2 -D torus Non-integrable → motion on 3 -D constant E surface Chaos ? Poincare sections transverse to 3 -D constant E surface is 2 -D Integrable system ( sets of nested tori with separatrices ): • Series of discrete points → periodic • Closed paths around point → quasi-periodic orbits around elliptic point • Hyperbolic orbits near hyperbolic points

Henon-Heiles, almost integrable

KAM Theorem Let H 0 integrable KAM theorem (criteria dropped): Tori that survive perturbation satisfy g(ε) increases monotonically with ε Implication: • For ε > 0, all tori with rational W break up • (KAM) tori with irrational W persist, then break up 1 by 1 as ε increases • Last to be destroyed has golden mean ratio ( most irrational ) Qualitative explanation: • W rational → motion sustained by strong resonances between overlapping harmonics • → any perturbation will remove overlappings • → rapid break up of tori

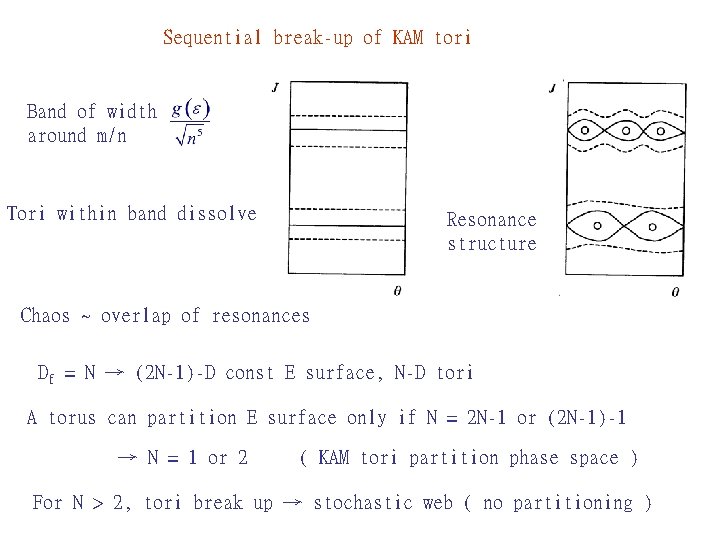
Sequential break-up of KAM tori Band of width around m/n Tori within band dissolve Resonance structure Chaos ~ overlap of resonances Df = N → (2 N-1)-D const E surface, N-D tori A torus can partition E surface only if N = 2 N-1 or (2 N-1)-1 → N = 1 or 2 ( KAM tori partition phase space ) For N > 2, tori break up → stochastic web ( no partitioning )

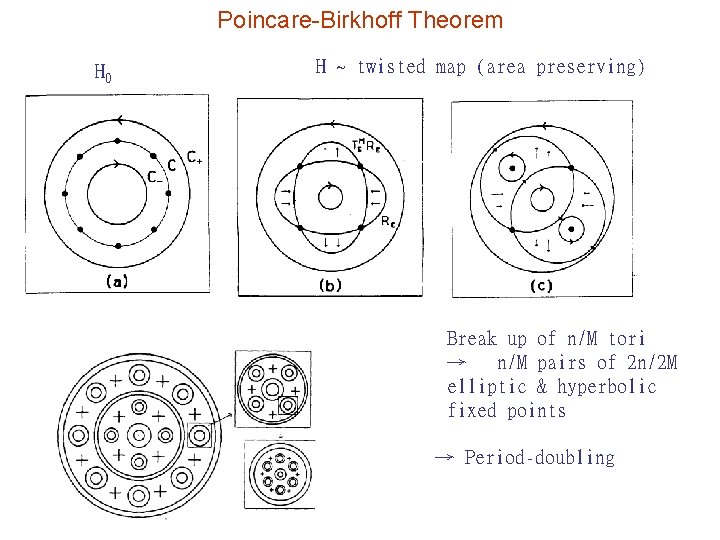
Poincare-Birkhoff Theorem H 0 H ~ twisted map (area preserving) Break up of n/M tori → n/M pairs of 2 n/2 M elliptic & hyperbolic fixed points → Period-doubling

Insets & outsets of hyperbolic point dissolve first → homoclinic & heteroclinc tangles → chaos? Different I. C. may lead to q. p. /chaotic motion For Df 2, surviving KAM tori confine chaotic motion near broken tori For Df 3, chaos from any broken torus can roam mostly freely (Arnold diffusion). Lyapunov exponent: • Σλi = 0 for conservative system • Chaos: at least 1 λi > 0 Monodromy matrix M : z = periodic orbit Eigenvalues μi of M ~ Floquet multipliers: Πμi = 1 μi comes in pairs of (μ, μ-1 )

Period-Doubling Break up of m/n tori • m/n pairs of 2 m/2 n elliptic & hyperbolic fixed points • Period doubling • ε increases → further period doubling … • δH = 8. 721097…, αH = -4. 01807… Period-n-tuplings are common in Hamiltonian systems Cause: resonances among constituent nonlinear oscillators Meyer's theorem: 5 types of bifurcations Singularities in H can also cause non-integrability E. g. , billiard balls

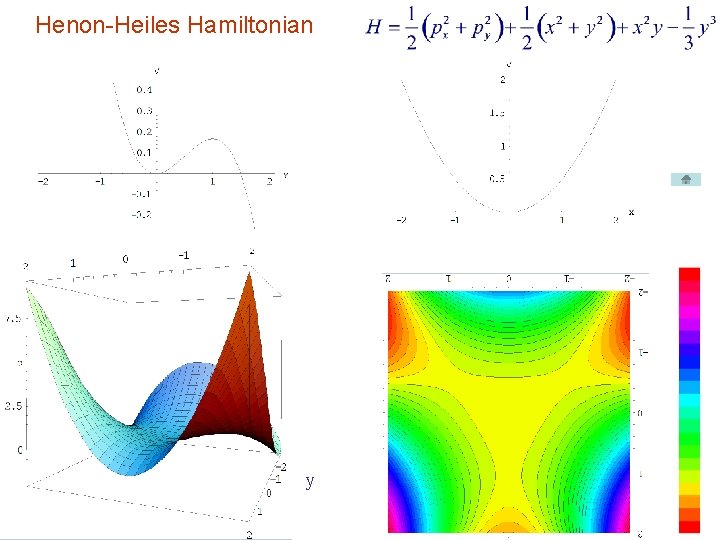
Henon-Heiles Problem A star in axially symmetric galaxy; • Nf = 3 • Known integrals of motion: E, Lz • No known analytic form of 3 rd integral • If 3 rd integral not exist → σ(vρ) σ(vz) • Observed: σ(vρ) : σ(vz) = 2 : 1 Henon-Heiles model:

Henon-Heiles Hamiltonian y

Height of potential well around 0 is 1/6 → bound orbits for E < 1/6 Hamilton's eqs: Nf = 2 → 3 -D const E surface → 2 -D Poincare section → Choice: y-py plane at x = 0

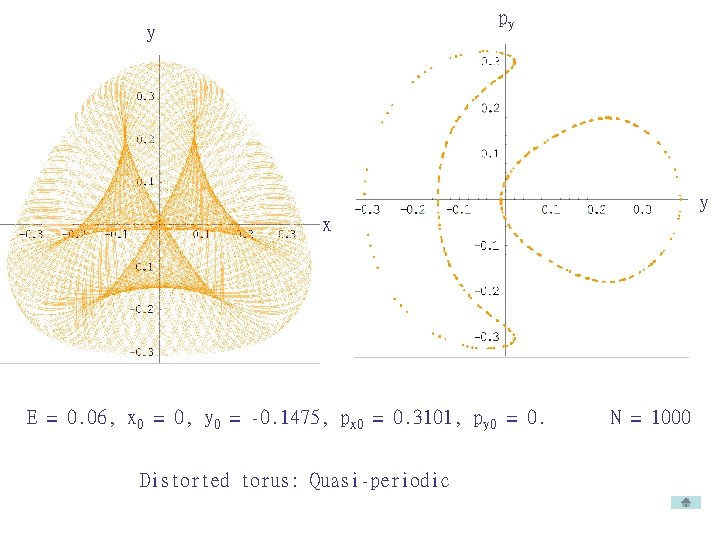
py y y x E = 0. 06, x 0 = 0, y 0 = -0. 1475, px 0 = 0. 3101, py 0 = 0. Distorted torus: Quasi-periodic N = 1000

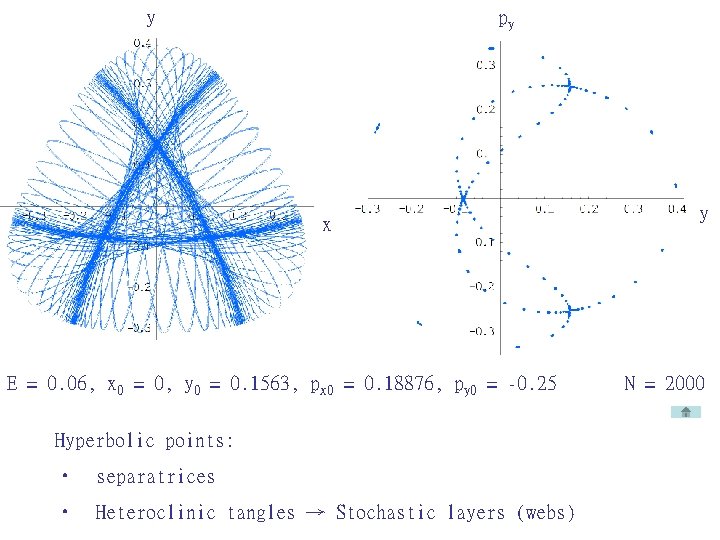
y py x E = 0. 06, x 0 = 0, y 0 = 0. 1563, px 0 = 0. 18876, py 0 = -0. 25 Hyperbolic points: • separatrices • Heteroclinic tangles → Stochastic layers (webs) y N = 2000

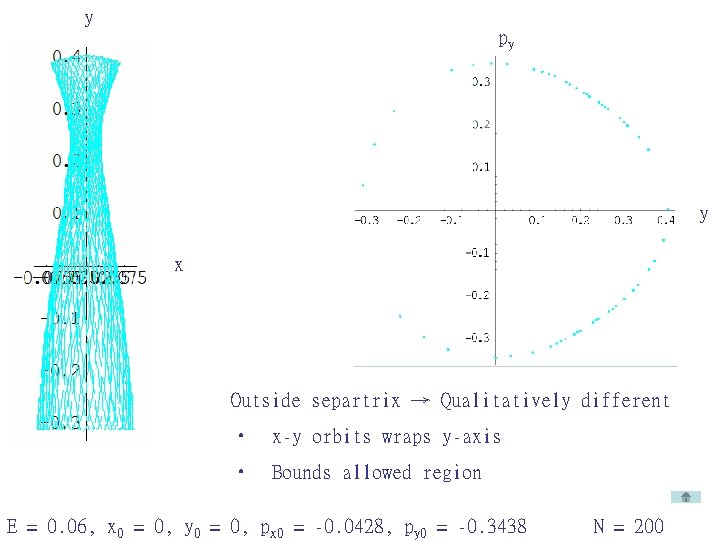
y py y x Outside separtrix → Qualitatively different • x-y orbits wraps y-axis • Bounds allowed region E = 0. 06, x 0 = 0, y 0 = 0, px 0 = -0. 0428, py 0 = -0. 3438 N = 200

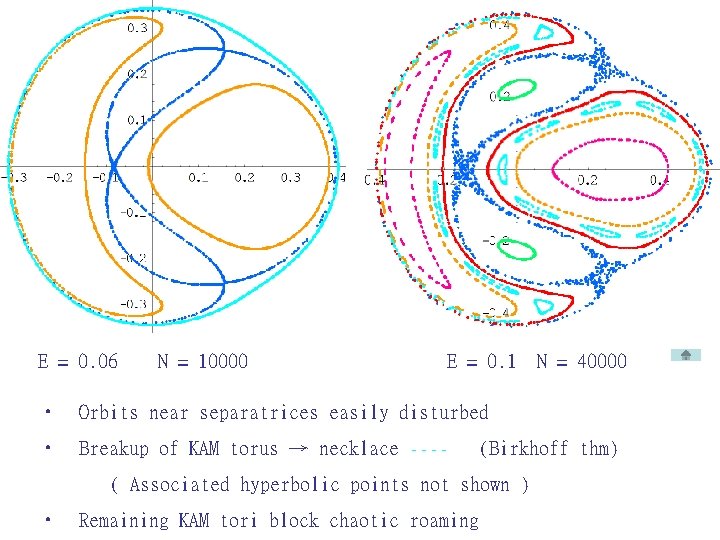
E = 0. 06 N = 10000 E = 0. 1 N = 40000 • Orbits near separatrices easily disturbed • Breakup of KAM torus → necklace ---- (Birkhoff thm) ( Associated hyperbolic points not shown ) • Remaining KAM tori block chaotic roaming

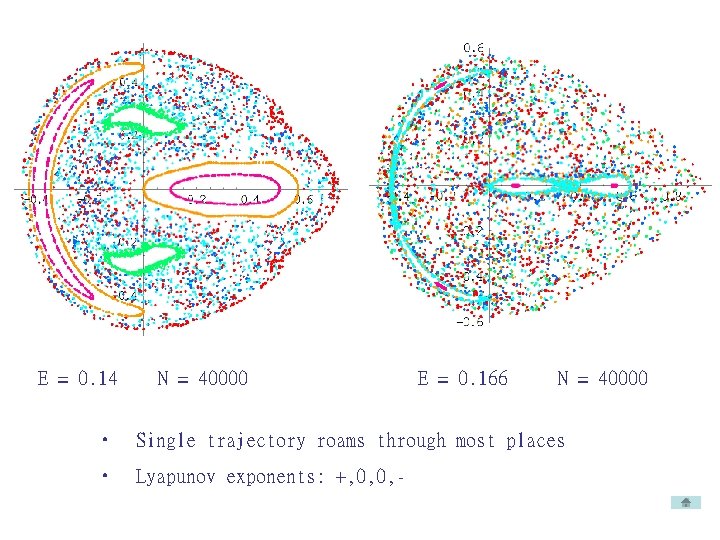
E = 0. 14 N = 40000 E = 0. 166 N = 40000 • Single trajectory roams through most places • Lyapunov exponents: +, 0, 0, -

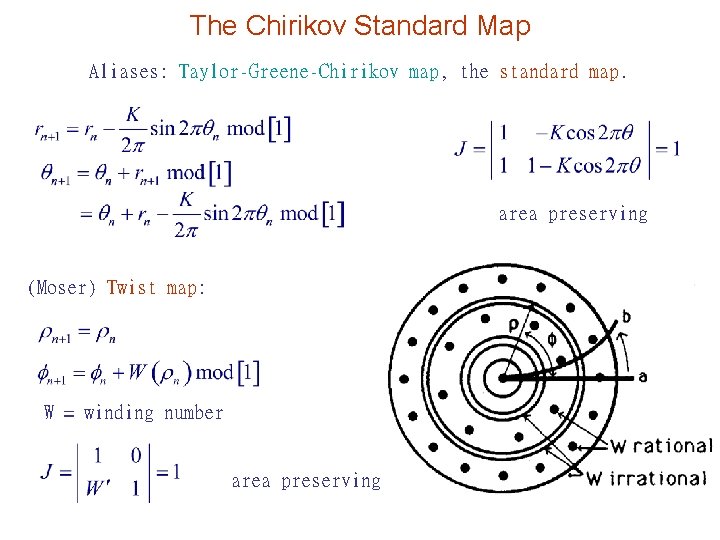
The Chirikov Standard Map Aliases: Taylor-Greene-Chirikov map, the standard map. area preserving (Moser) Twist map: W = winding number area preserving

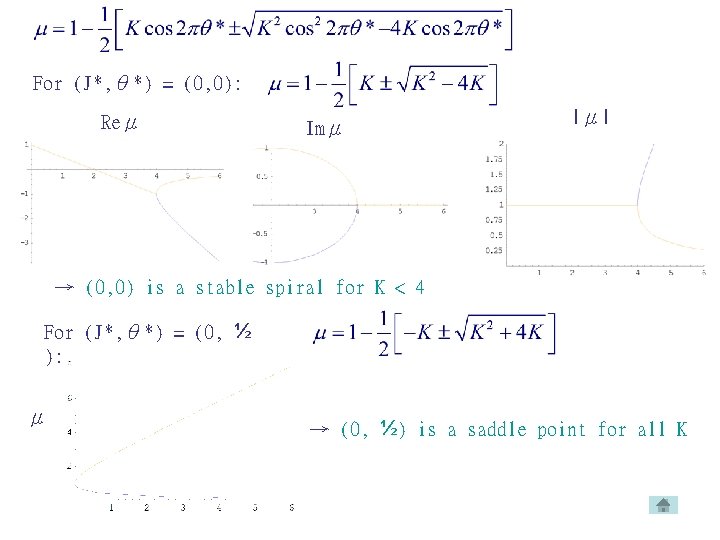
Fixed points ( with r → J ): → → K < 2π → Near fixed point: Floquet multipliers: m = 0 and θ* = 0, ½ m, p = integers

For (J*, θ*) = (0, 0): Reμ Imμ |μ| → (0, 0) is a stable spiral for K < 4 For (J*, θ*) = (0, ½ ): μ → (0, ½) is a saddle point for all K

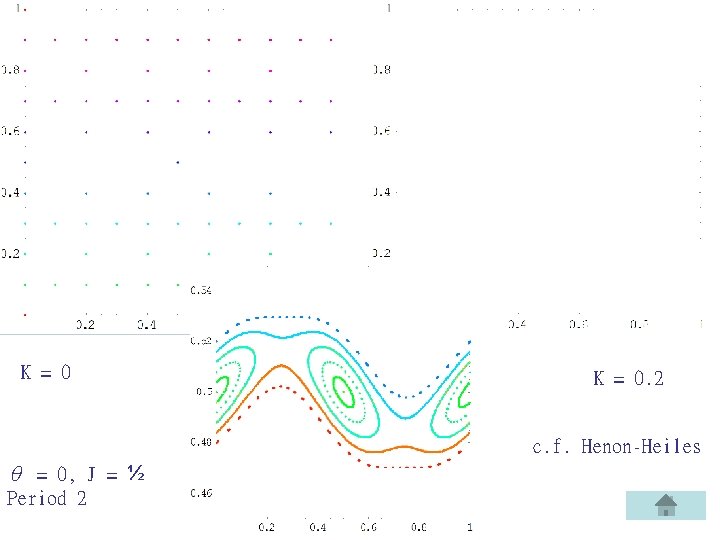
K = 0. 2 c. f. Henon-Heiles θ = 0, J = ½ Period 2

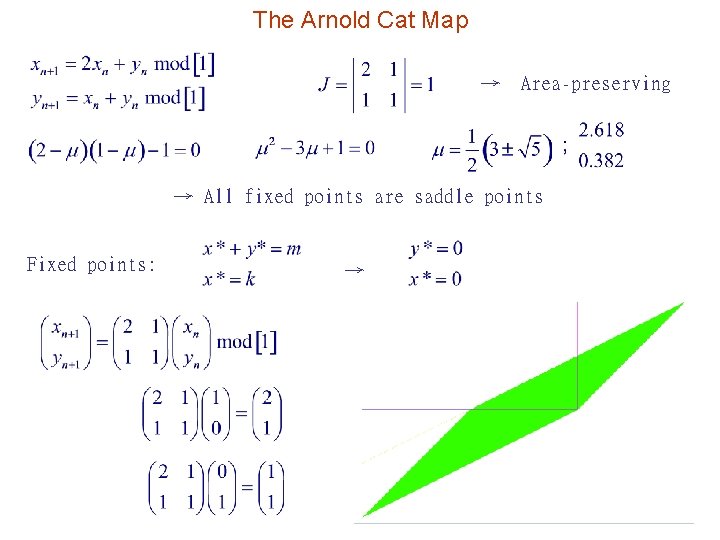
The Arnold Cat Map → Area-preserving → All fixed points are saddle points Fixed points: →

→ ↓ ← Ex 8. 8 -1: Fixed points of f(n) have rational coordinates

Evolution of 1 -D conservative system: → ( n ~ tn ) Fourier analysis: → Spread to new modes, But not IC sensitive

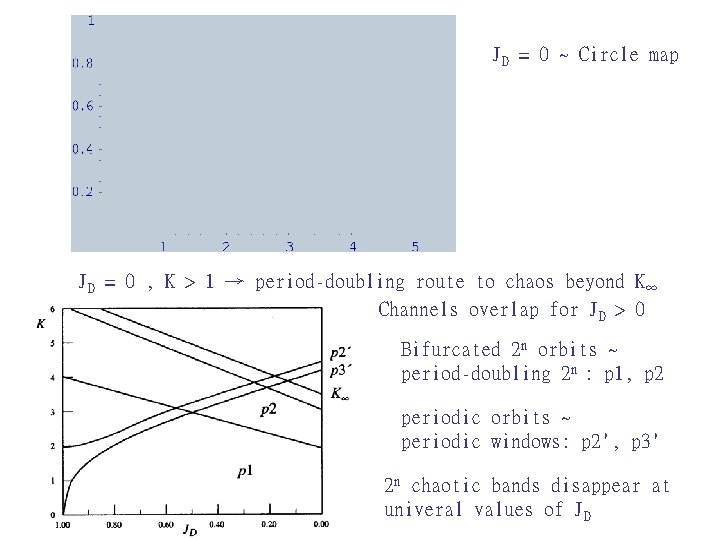
The Dissipative Standard Map G. Schmidt, B. H. Wang, PR A 32, 2994 (85) Dissipative for JD < 1 JD = 0 : ( Sine circle map with Ω = 0)

JD = 0 ~ Circle map JD = 0 , K > 1 → period-doubling route to chaos beyond K∞ Channels overlap for JD > 0 Bifurcated 2 n orbits ~ period-doubling 2 n : p 1, p 2 periodic orbits ~ periodic windows: p 2', p 3' 2 n chaotic bands disappear at univeral values of JD

Applications • Billiards (elastic collisions, piecewise linear) – – Rectangular or circular walls → periodic / q. p. stadium / Sinai billiards ( round obstacle ) → chaotic for some orbits 2 balls + gravity: All kinds of behavior Quantum chaos • Astronomical Dynamics – Orbits of Pluto & some asteroids may be chaotic – Kuiper objects • Particle Accelerators – Avoid possible chaotic trajectories in accelerator design • Superconductivity – Vortex structures under magnetic field (type II superconductors) phaselocking, Arnold tongues, Farey tree, devil's staircase • Optics – small dielectric spheres: whispering gallery lasers – Spheres distorted → chaos