Management Science Hamiltonian Circuits introduction 1 Whats the















- Slides: 23

Management Science Hamiltonian Circuits • introduction 1

What’s the difference? • Euler Circuit Problems: Problems where travel along every EDGE was required 2

What’s the difference? • Hamiltonian Circuit Problems: Problems that require travel To every VERTEX 3

Ch 6: Vocabulary • Hamilton Path: path that passes through every vertex of the graph • Hamilton Circuit: circuit that visits each vertex only once (except where it returns to the starting vertex) v. Note – Hamilton Paths and circuits are NOT mutually exclusive of one another! 4

Ch 6: Vocabulary • Complete Graph: every pair of vertices is joined by exactly one edge. Each of the N vertices has degree N-1 – Total number of edges KN = N(N-1)/2 – KN has the most edges of any graph of N vertices as long as there are no loops or multiple edges. 5

Ch 6: Vocabulary • Weighted Graph: a graph whose edges have numbers attached to them. – Weights – numbers could represent time, money, or distance. 6

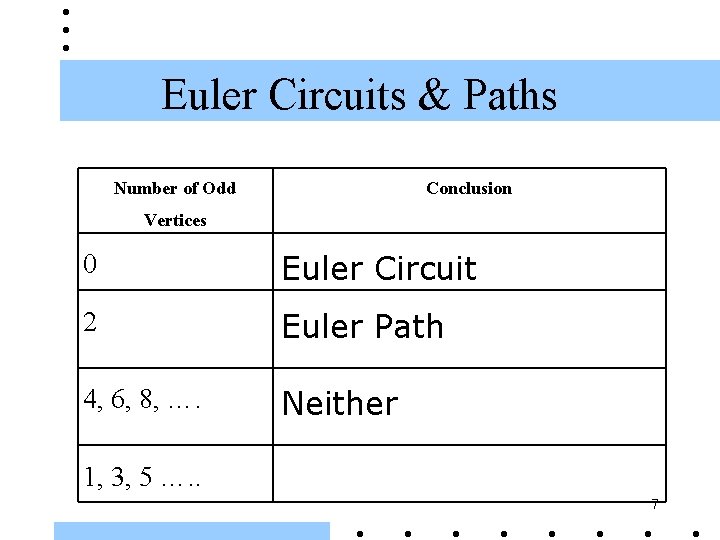
Euler Circuits & Paths Number of Odd Conclusion Vertices Euler Circuit 0 2 4, 6, 8, …. 1, 3, 5 …. . Euler Path Neither 7

Hamilton Circuits 1. Dirac’s Theorem – If a connected graph has N vertices (N>2) and all of them have degree bigger than or equal to N/2, then the graph has a Hamilton Circuit. 8

Hamilton’s Circuits 2. If a graph is complete it has a Hamilton Circuit. 9

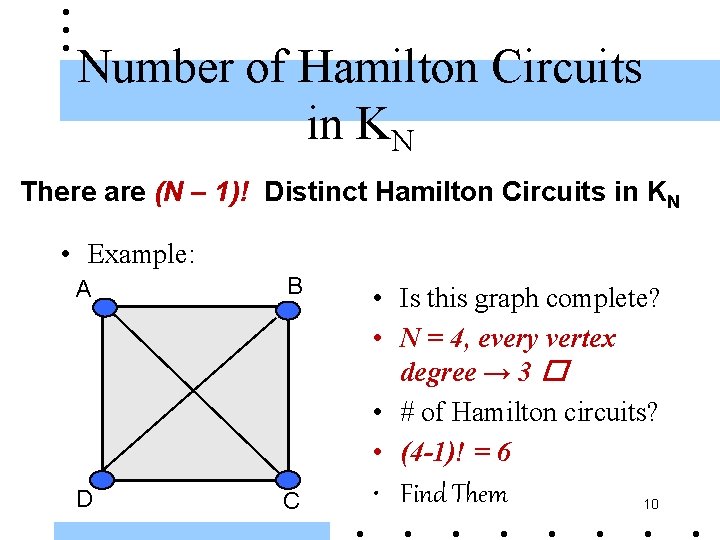
Number of Hamilton Circuits in KN There are (N – 1)! Distinct Hamilton Circuits in KN • Example: A B • Is this graph complete? • N = 4, every vertex degree → 3 � • # of Hamilton circuits? • (4 -1)! = 6 D C • Find Them 10

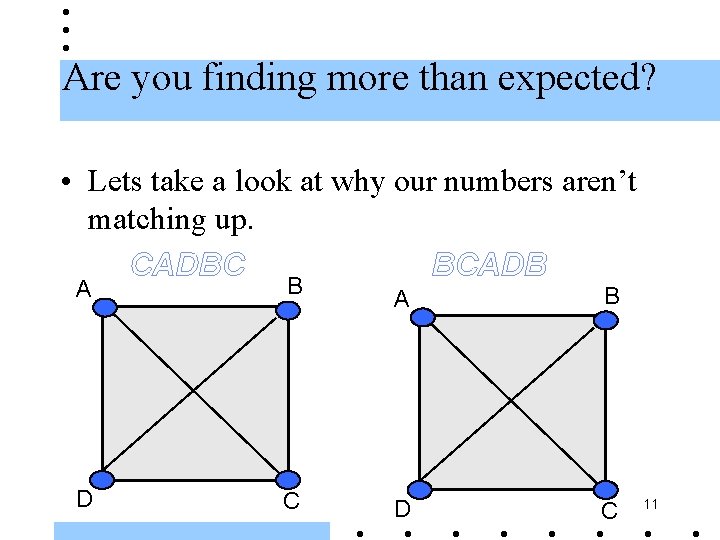
Are you finding more than expected? • Lets take a look at why our numbers aren’t matching up. CADBC BCADB A B D C 11

There are (N – 1)! Distinct Hamilton Circuits in KN If it is the same circuit, but different reference point, It is not distinct 12

Find all 6 DISTINCT HC’s 1. 2. 3. 4. 5. 6. ABCDA ABDCA ACBDA ACDBA ADBCA ADCBA Mirror images 13

Mirror images 1. ABCDA ADCBA 2. ABDCA ACDBA 3. ACBDA ADBCA 14

Factorials N 1 2 3 4 5 6 7 8 9 10 (N-1)! Remember…… (6)! = 6 x 5 x 4 x 3 x 2 x 1 15

• Factorial Examples 16

EXAMPLES OF HAMILTONIAN CIRCUIT PROBLEMS • • The traveling salesman City bus routes (pick ups at a specific stop) Tour bus routes (to specific sites) Field trip routes (to specific displays/exhibits/areas of interest) 17

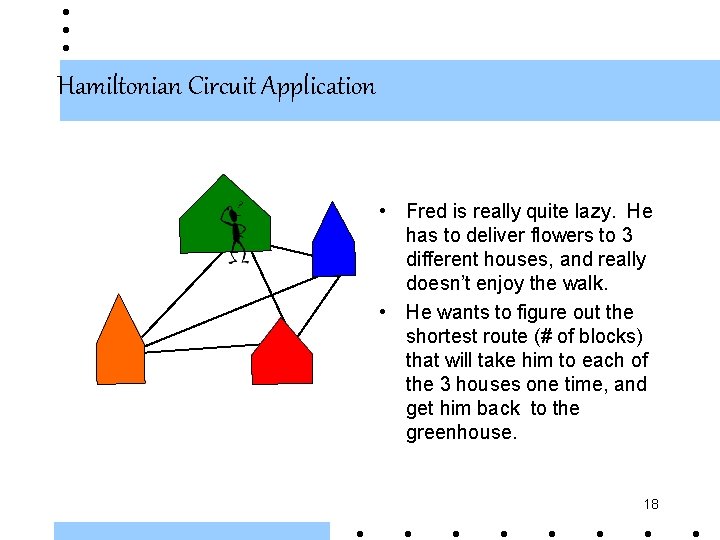
Hamiltonian Circuit Application • Fred is really quite lazy. He has to deliver flowers to 3 different houses, and really doesn’t enjoy the walk. • He wants to figure out the shortest route (# of blocks) that will take him to each of the 3 houses one time, and get him back to the greenhouse. 18

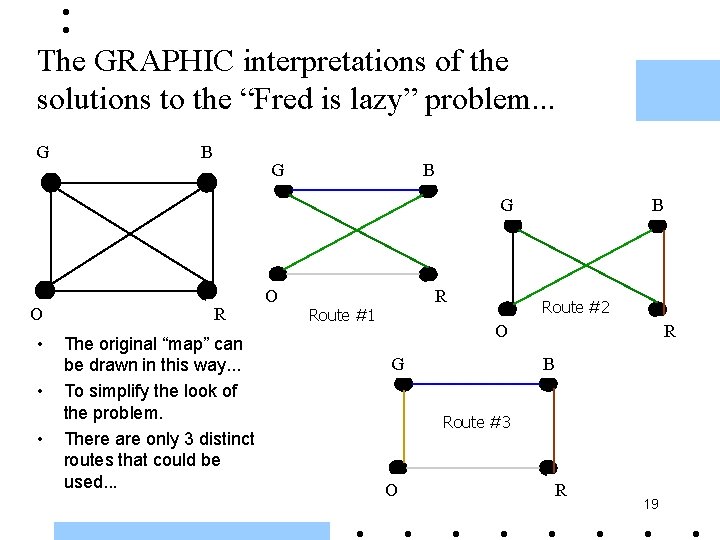
The GRAPHIC interpretations of the solutions to the “Fred is lazy” problem. . . G B G O • • • R The original “map” can be drawn in this way. . . To simplify the look of the problem. There are only 3 distinct routes that could be used. . . O R Route #1 B Route #2 O G R B Route #3 O R 19

Hamiltonian SUBGRAPHS. . . G B G B Route #3 Route #2 O Route #1 R O • You should notice that these 3 figures represent the ONLY possible routes Fred could take. • Each figure is called a SUBGRAPH of the original graph. • Each figure can be used to describe a number of 20 routes depending on the starting point. R

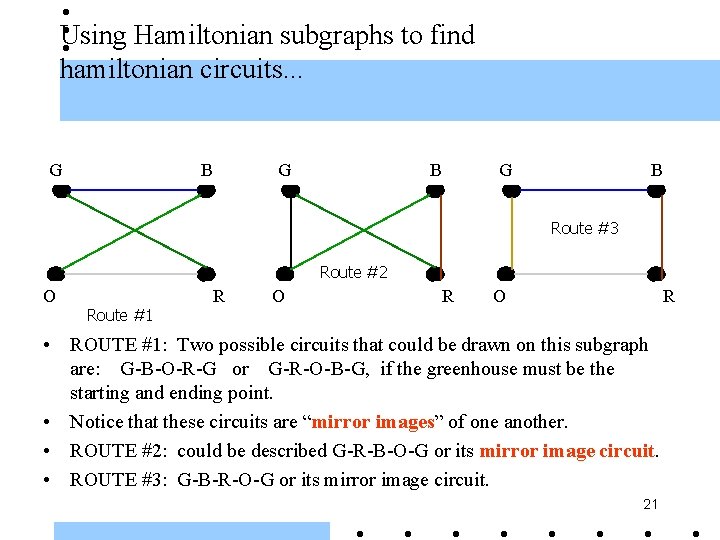
Using Hamiltonian subgraphs to find hamiltonian circuits. . . G B G B Route #3 Route #2 O Route #1 R O R • ROUTE #1: Two possible circuits that could be drawn on this subgraph are: G-B-O-R-G or G-R-O-B-G, if the greenhouse must be the starting and ending point. • Notice that these circuits are “mirror images” of one another. • ROUTE #2: could be described G-R-B-O-G or its mirror image circuit. • ROUTE #3: G-B-R-O-G or its mirror image circuit. 21

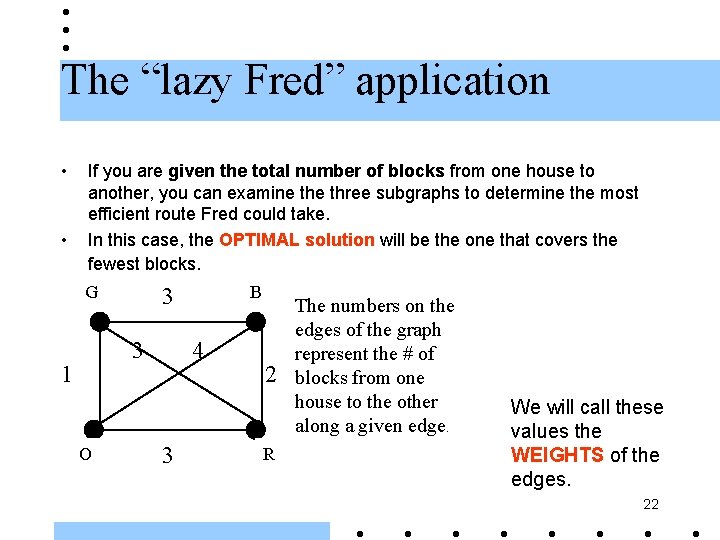
The “lazy Fred” application • • If you are given the total number of blocks from one house to another, you can examine three subgraphs to determine the most efficient route Fred could take. In this case, the OPTIMAL solution will be the one that covers the fewest blocks. G 3 1 O B 3 4 3 2 R The numbers on the edges of the graph represent the # of blocks from one house to the other along a given edge. We will call these values the WEIGHTS of the edges. 22

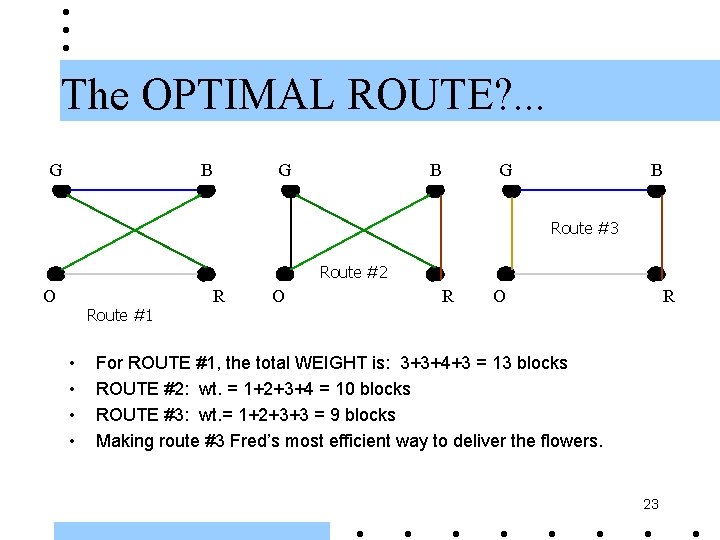
The OPTIMAL ROUTE? . . . G B G B Route #3 Route #2 O Route #1 • • R O R For ROUTE #1, the total WEIGHT is: 3+3+4+3 = 13 blocks ROUTE #2: wt. = 1+2+3+4 = 10 blocks ROUTE #3: wt. = 1+2+3+3 = 9 blocks Making route #3 Fred’s most efficient way to deliver the flowers. 23