Graph Theory Chapter 8 Hamiltonian Graphs DaYeh Univ

Graph Theory Chapter 8 Hamiltonian Graphs 大葉大學(Da-Yeh Univ. ) 資訊 程系(Dept. CSIE) 黃鈴玲(Lingling Huang)

Outline 8. 1 An Introduction to Hamiltonian Graphs 8. 2 Which Graphs are Hamiltonian? 8. 3 The Traveling Salesman Problem Ch 8 -2 Copyright 黃鈴玲

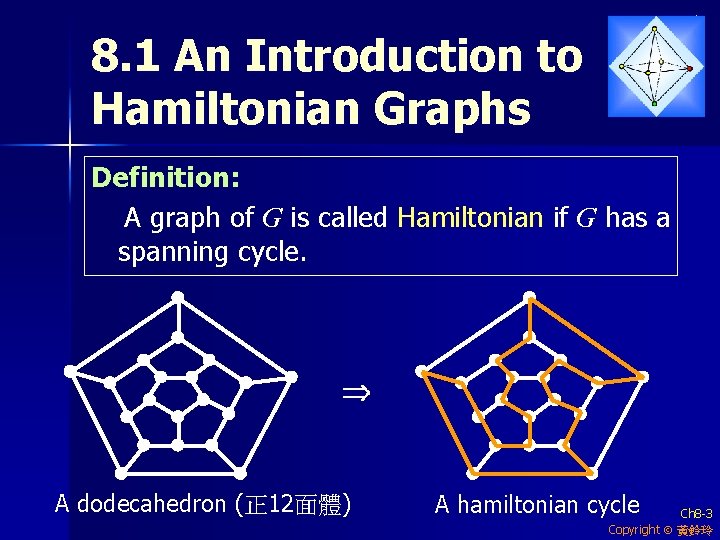
8. 1 An Introduction to Hamiltonian Graphs Definition: A graph of G is called Hamiltonian if G has a spanning cycle. A dodecahedron (正 12面體) A hamiltonian cycle Ch 8 -3 Copyright 黃鈴玲

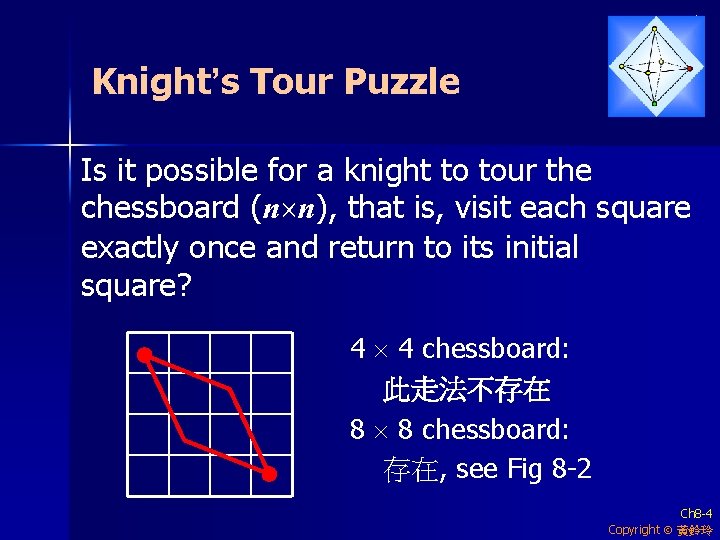
Knight’s Tour Puzzle Is it possible for a knight to tour the chessboard (n n), that is, visit each square exactly once and return to its initial square? 4 4 chessboard: 此走法不存在 8 8 chessboard: 存在, see Fig 8 -2 Ch 8 -4 Copyright 黃鈴玲

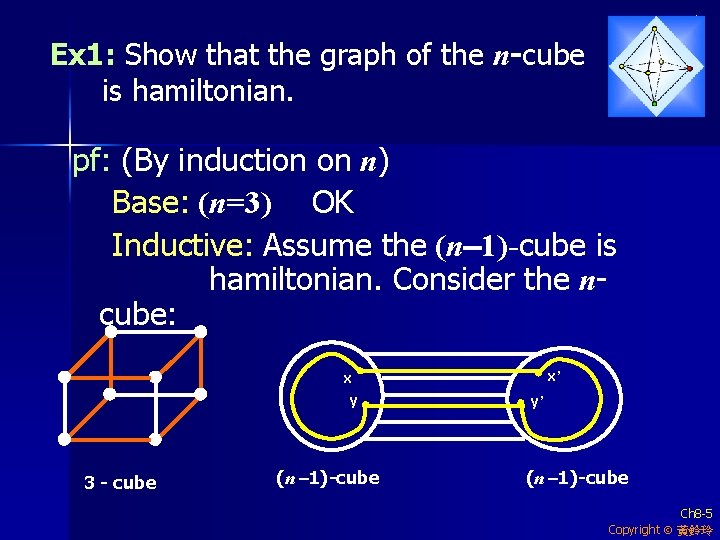
Ex 1: Show that the graph of the n-cube is hamiltonian. pf: (By induction on n) Base: (n=3) OK Inductive: Assume the (n-1)-cube is hamiltonian. Consider the ncube: x’ x y 3 - cube (n -1)-cube y’ (n -1)-cube Ch 8 -5 Copyright 黃鈴玲

Ex 2: Show that the graph G below is not hamiltonian. Hint: 考慮通過此三點的edge hamiltonian cycle 必定包含這些edge. 本身已構成cycle， 故不可能hamiltonian Ch 8 -6 Copyright 黃鈴玲

Observe: 1. Cn (n 3) is hamiltonian. 2. Kn (n 3) is hamiltonian. 3. A connected graph with cut-vertices is not hamiltonian. Ch 8 -7 Copyright 黃鈴玲

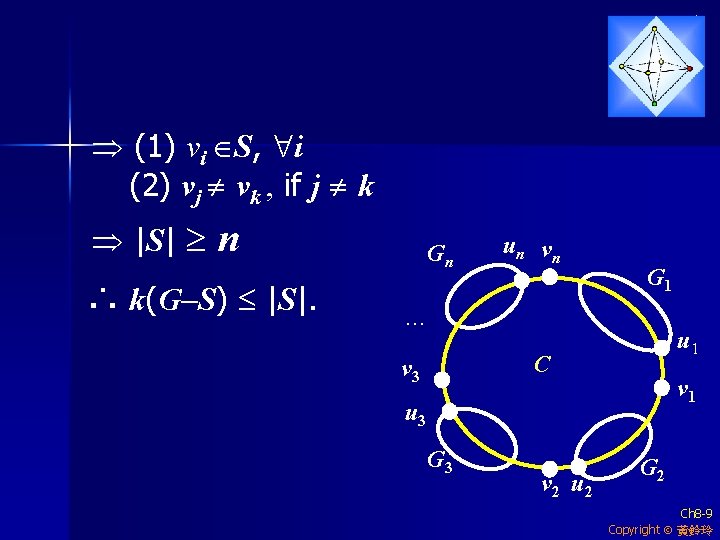
Thm 8. 1: If G is hamiltonian, than k(G - S) |S| for every S V(G), S . pf: G is hamiltonian a hamiltonian cycle C Suppose k(G-S) = n, where G 1, G 2, …, Gn are components of G-S. Let ui (1 i n) be the last vertex of C that belongs to Gi. un v n Gn G 1 Let vi be the vertex … that immediately u 1 C v 3 follows ui on C. v 1 u 3 (ui的下一點即是vi且vi S) G 3 v 2 u 2 G 2 Ch 8 -8 Copyright 黃鈴玲

(1) vi S, i (2) vj vk , if j k | S| n ∴ k(G-S) |S | |. Gn un v n G 1 … u 1 C v 3 v 1 u 3 G 3 v 2 u 2 G 2 Ch 8 -9 Copyright 黃鈴玲

Ex 5: Show that no bipartite graph of odd order is hamiltonian. pf: 例如K 2, 3 上與下兩個part 點數不一致 ∴無法有 hamiltonian cycle Ch 8 -10 Copyright 黃鈴玲

Homework Exercise 8. 1: 1, 2, 3, 4, 5 Ch 8 -11 Copyright 黃鈴玲

Outline 8. 1 An Introduction to Hamiltonian Graphs 8. 2 Which Graphs are Hamiltonian? 8. 3 The Traveling Salesman Problem Ch 8 -12 Copyright 黃鈴玲

8. 2 Which Graphs are Hamiltonian? Thm 8. 2 (Dirac’s Thm) G: order p 3 If deg(v) p/2 v V(G), then G is Hamiltonian. Pf: (1) If p = 3 deg(v) 2 v V(G) G C 3 (2) If p 4, let P: v 1 , v 2 , …, vn be a longest path in G. v 1 v 2 v 3 vn vn-1 Ch 8 -13 Copyright 黃鈴玲

Then every neighbor of v 1 and vn is on P. ∵ deg(v) p/2 ∴ n 1+p/2 Claim: vi V(P), 2 i n, s. t. , v 1~ vi and vi-1~ vn. pf of claim: v 1 v 2 v 3 v i-1 vi vn-1 vn If not, vj with vj ~ v 1 vj-1 ~ vn ∵ deg(v 1) p/2 ∴v 1到vn-1中至少有 p/2 個點與v 個點與 n不相連 ∵ deg(vn) p/2 ∴此path 至少有 p/2 + 1 個點 Ch 8 -14 (vn) Copyright 黃鈴玲

Let C: v 1, v 2, …, vi-1, vn-1, …, vi, v 1 C is a cycle of length n. If n<p then u V(G-C) ∵ deg(u) p/2, |V(C)| = n 1+ p/2 ∴ vk s. t. u ~ vk (1 k n) ∴ C∪{uv ∪{ k} contains a path longer than P. v 1 vn-1 n=p vi v i-1 v v 2 vn 3 C is a Hamiltonian cycle. ※ Thm 8. 2 中 deg(v) p/2 的條件若改為 (p-1)/2 則不保證存在 hamiltonian cycle. 例: Kn, n+1 Ch 8 -15 Copyright 黃鈴玲

※Thm 8. 2 不能cover 的例子: (1) Cn (n 5): hamiltonian p 5, deg(vi) = 2< p/2 i (2) +(Km U Kn): hamiltonian p=m+n+2 Suppose m < n, deg(v) = m + 1 < p/2 if v V(Km) Fig 8 -5: +(K 2 U K 3) Ch 8 -16 Copyright 黃鈴玲

Thm 8. 3 Let G be a graph of order p 3. Suppose u and v are nonadjacent vertices of G s. t. deg(u) + deg(v) p. Then G is hamiltonian iff G+uv is hamiltonian. Pf: “ ”: trivial. “ ”: Let C be a hamiltonian cycle of G+uv. If uv C G is hamiltonian. If uv C spanning u-v path P (P = Cuv) Ch 8 -17 Copyright 黃鈴玲

P: u v (P上使用了所有點) Similar as the proof of Thm 8. 2, G has a hamiltonian cycle. Ch 8 -18 Copyright 黃鈴玲

Def: A closure c(G) of a graph G of order p is a graph obtained from G by recursively joining pairs of nonadjacent vertices whose degree sum is at least p until no such pairs remain. ※ c(G) is unique. Ch 8 -20 Copyright 黃鈴玲

Thm 8. 5 G is hamiltonian c(G) is hamiltonian. Cor 8. 5(a) Let G be a graph of order p 3. If c(G) Kp , then G is hamiltonian. Fig 8. 7 G c(G) K 9 G is hamiltonian. Ch 8 -21 Copyright 黃鈴玲

Cor 8. 5(b) |V(G)| = p 3. u, v V(G). If deg(u) + deg(v) p u ~ v, then G is hamiltonian. Cor 8. 5(c) |V(G)| = p 3. Let d 1, d 2, …dp be the degree sequence of G with d 1 d 2 … dp. Suppose for every k < p/2, dk k dp-k p - k. Then G is hamiltonian. Cor 8. 5(d) |V(G)| = p, |E(G)| = q. If q , then G is hamiltonian. Ch 8 -22 Copyright 黃鈴玲

Ex 5. Show that if a graph of order at least 3 has an isolated vertex or an end-vertex, then its closure is not complete. pf: (1) If u is an isolated vertex of graph G, then deg(u) = 0, deg(v) p-2 for every vertex v u. In c(G), u ~ v u v c(G) Kp (2) If u is an end-vertex then deg(u) = 1, deg(v) p-2 if u ~ v c(G) Kp Ch 8 -23 Copyright 黃鈴玲

Homework Exercise 8. 2: 1, 3, 4, 8, 9, 11 Ch 8 -24 Copyright 黃鈴玲

Outline 8. 1 An Introduction to Hamiltonian Graphs 8. 2 Which Graphs are Hamiltonian? 8. 3 The Traveling Salesman Problem Ch 8 -25 Copyright 黃鈴玲

8. 3 The Traveling Salesman Problem TSP: Suppose that a salesman is required to make a round trip through a given collection of p( 3) cities. What route should he take to minimize the total distance traveled? G: connected weighted graph, vi V(G): the cities, w(vivj) of edge vivj: the distance to travel directly between vi and vj. (Assume that G is complete) ※ TSP asks for a Hamiltonian cycle of minimum weight. Ch 8 -26 Copyright 黃鈴玲

∵NP-complete ∴改成 find low weight 的 HC TSP: Given a weighted complete graph G and a positive constant B, does there exist a hamiltonian cycle C in G so that w(C) B? 此處提供兩種作法 前提: 需先符合triangle inequality (三角不等式) w(vi, vk) w(vi, vj) + w(vj, vk) vi vj vk Ch 8 -27 Copyright 黃鈴玲

Algorithm 8. 1 (a greedy algorithm) [ To determine a low weight HC in a weighted complete graph G of order p 3 satisfying the triangle inequality. ] 1. n 1. (n is the cycle length) 2. Select any vertex of G to form Cn. (Cn剛開始只有一個點) 3. If n < p, then find a vertex vn not on Cn s. t. w(unvn) is minimum for some un is on Cn, and go to Step 4. Otherwise, Cn is the desired HC. 4. Let Cn+1 be the (n+1)-cycle obtained by inserting vn immediately before un on Cn. 5. n n +1 and return to Step 3. Ch 8 -28 Copyright 黃鈴玲

Fig 8 -10 v 1 v 2 v 3 v 4 v 5 v 6 1. C 1: v 1 2. ∵ v 2, …, v 6中，w(v 1 v 4)最小 ∴C 2: v 1 v 4 v 1 v 2 v 3 v 5 v 6 3. v 1 v 4 ∵ w(v 3 v 4) 最小 ∴C 3: v 1 v 3 v 4 v 1 (加在要連的點之前) Ch 8 -29 Copyright 黃鈴玲

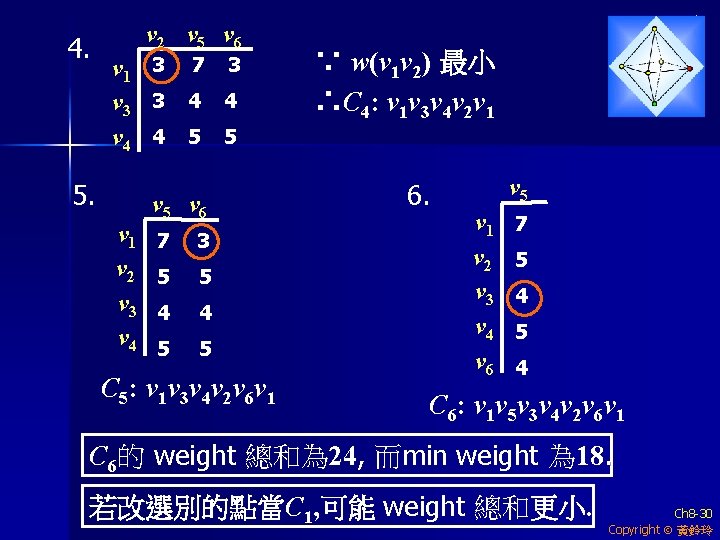
4. v 2 v 5 v 6 v 1 3 7 3 v 3 3 4 4 v 4 4 5 5 5. v 1 v 2 v 3 v 4 v 5 v 6 7 3 5 5 4 4 5 5 C 5: v 1 v 3 v 4 v 2 v 6 v 1 ∵ w(v 1 v 2) 最小 ∴C 4: v 1 v 3 v 4 v 2 v 1 6. v 5 v 1 v 2 v 3 v 4 v 6 7 5 4 C 6: v 1 v 5 v 3 v 4 v 2 v 6 v 1 C 6的 weight 總和為 24, 而min weight 為 18. 若改選別的點當C 1, 可能 weight 總和更小. Ch 8 -30 Copyright 黃鈴玲

Thm 8. 8 C : a HC given by Algorithm 8. 1 Cm : min weight HC w (C ) 2 w (C m ) (Algorithm 8. 1不保證能找出min HC, 但用 Algorithm 8. 1 找出的cycle 其weight 不會大於 min HC 的兩倍. ) Ch 8 -31 Copyright 黃鈴玲

Algorithm 8. 2 (利用 min spanning tree) [ To determine a low weight HC in a weighted complete graph G of order p 3 satisfying the triangle inequality. ] 1. Find a min spanning tree T of G. 2. Conduct a depth-first search of T. (起點為 T 的leaf) 3. If vi 1, vi 2, …, vip is the order in which the vertices of T are visited in step 2, then output the hamiltonian cycle vi 1, vi 2, …, vip, vi 1. (Algorithm 8. 2 找出的cycle 其 weight 也不會大於 min HC 的兩倍. ) Ch 8 -32 Copyright 黃鈴玲

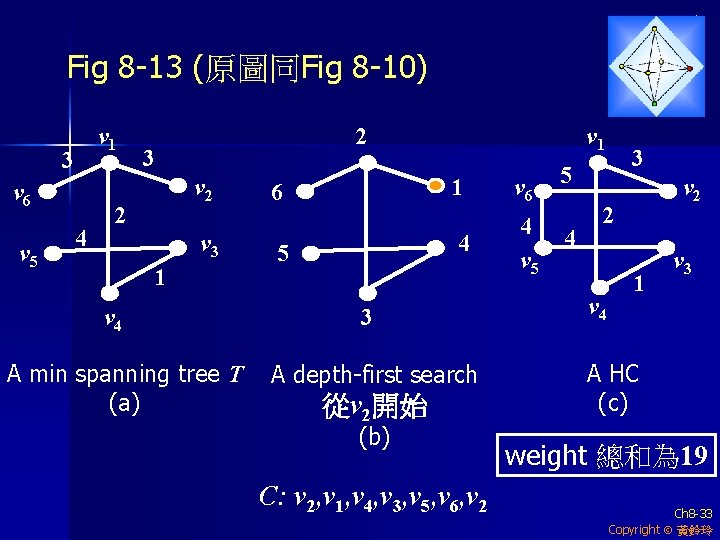
Fig 8 -13 (原圖同Fig 8 -10) v 1 3 v 6 v 5 4 2 3 v 2 2 v 3 1 v 4 A min spanning tree T (a) 6 5 v 1 1 v 6 5 4 4 v 5 4 3 A depth-first search 從v 2開始 (b) C: v 2, v 1, v 4, v 3, v 5, v 6, v 2 3 v 2 2 v 4 1 v 3 A HC (c) weight 總和為 19 Ch 8 -33 Copyright 黃鈴玲

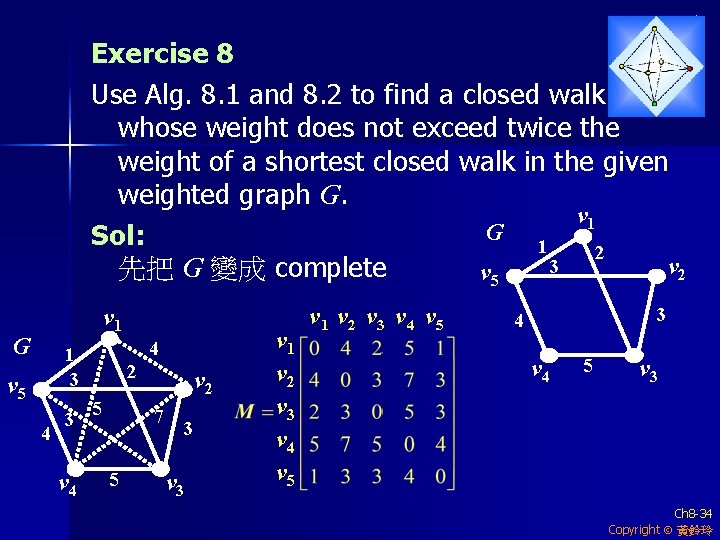
Exercise 8 Use Alg. 8. 1 and 8. 2 to find a closed walk whose weight does not exceed twice the weight of a shortest closed walk in the given weighted graph G. v 1 G Sol: 1 2 3 v 2 先把 G 變成 complete v 5 v 1 G 4 1 3 v 5 4 3 v 4 2 5 v 2 7 5 3 v 1 v 2 v 3 v 4 v 5 3 4 v 4 5 v 3 Ch 8 -34 Copyright 黃鈴玲

Homework Exercise 8. 3: 1, 3, 4, 8 Ch 8 -35 Copyright 黃鈴玲