Statistic multivariat prezentat de Valentin Clocotici Analiza factorial




































- Slides: 39

Statistică multivariată prezentată de Valentin Clocotici

Analiza factorială (2) Cursul nr. 11 05 -Nov-20 2

ACP/ACPN • Pentru început, o nouă definiţie a componentelor principale, care oferă un punct de vedere diferit (apropiat de sensul istoric iniţial). • Notăm cu Xn p matricea de date (n observaţii asupra a p variabile), cu Aj’ matricea (transpusă) (de tip j p) a ponderilor primelor j componente principale (coloanele din Aj fiind primii j vectori proprii), cu Zn j matricea scorurilor componentelor principale. zik = a 1 ix 1 k + a 2 ix 2 k + … + apixpk • Rezultă atunci X = Z Aj’ + U unde Un p este matricea reziduurilor. • Se poate arăta atunci că primele j componente principale sunt acele variabile necorelate care constituie cele mai bune variabile predictor (printr-un model liniar) ale variabilelor observate. • Criteriul este tot al celor mai mici pătrate 05 -Nov-20 3

ACP/ACPN • Se poate astfel spune că, dacă s-ar determina mulţimea de variabile necorelate care prognozează cel mai bine (printr-un model liniar) variabilele observate, atunci aceste noi variabile ar fi componentele principale. • Prin urmare, relaţia matriceală X = Z A j’ + U se interpretează ca evidenţiind variabilele ascunse (latente), z, care determină variabilele observate x. • Din toată discuţia de până acum apare ca un punct important acela al fixării numărului j de componente principale care se reţin în modelul final. • Această întrebare nu are un răspuns precis. Există o serie de proceduri acceptate, discutate în continuare şi care se aplică şi altor metode factoriale. 05 -Nov-20 4

Numărul de axe factoriale Criteriul Cattell (scree test) • Varianta grafică: se detectează pe diagrama valorilor proprii un “cot”. Se reţin doar valorile proprii de până în acel loc, inclusiv. • Varianta analitică: se calculează • Analog, se încearcă trasarea unei drepte (dreapta de regresie) prin ultimele j valori proprii şi se reţin doar valorile proprii situate deasupra acesteia. 1= 1 - 1, 2= 2 - 3, … 1= 1 - 2, 2= 2 - 3, … şi se reţin 1, …, k+1 astfel încât 1, 2, …, k să fie toate pozitive. 05 -Nov-20 5

Numărul de axe factoriale • O proprietate importantă a metodei este aceea a menţinerii varianţei totale a datelor. Cu alte cuvinte • În cazul ACPN, variabilele sunt standardizate şi, prin urmare, de unde rezultă că suma varianţelor componentelor principale este p: 05 -Nov-20 6

Numărul de axe factoriale • În general, primele q componente principale oferă un rezumat q-dimensional al variabilelor iniţiale, acela care varianţa maximă dintre toate rezumatele q-dimensionale. • Pentru q = p nu are loc o reducere a dimensiunii, obţinând o simplă transformare a variabilelor iniţiale. • Prin reţinerea doar a primelor q valori proprii, proporţia explicată din varianţa totală este • Acesta nu poate constitui un criteriu pentru numărul de factori reţinuţi, întrucât raportul creşte o dată cu numărul factorilor (ajungând la 1). 05 -Nov-20 7

Numărul de axe factoriale • Un prim criteriu poate fi acela al reţinerii acelor valori proprii care depăşesc media, adică criteriul implicit în SPSS, cu observaţia că în ACPN criteriul devine Criteriul Kaiser • Se reţin doar componentele principale corespunzând valorilor proprii mari decât 1. • Se aplică de regulă în ACPN. 05 -Nov-20 8

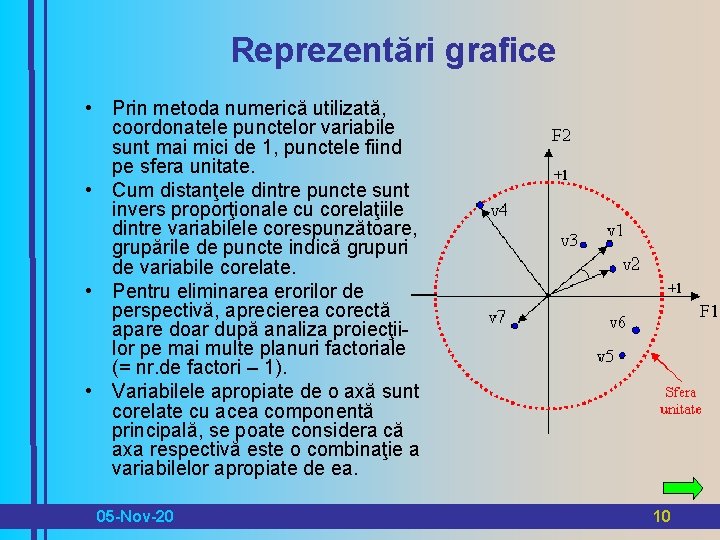
Reprezentări grafice • In ACP/ACPN datele iniţiale se referă la n observaţii asupra a p variabile, care pot fi interpretate ca – n puncte-indivizi (observaţii) în Rp, – p puncte-variabile în Rn. • Reţinerea unui număr de axe factoriale echivalează cu determinarea unui subspaţiu în care datele iniţiale pot fi regăsite cu suficientă acurateţe. • Examinarea structurii norilor de puncte din subspaţiile respective se realizează prin metode grafice, reprezentând punctele prin proiecţii pe un număr suficient de planuri factoriale. • Astfel, pentru a putea înţelege structura unui nor de puncte în R 3 este nevoie de proiecţia lor pe două planuri (x. Oy şi x. Oz, de exemplu). • Interpretările diferă totuşi după cum este vorba de variabile sau de observaţii. 05 -Nov-20 9

Reprezentări grafice • Prin metoda numerică utilizată, coordonatele punctelor variabile sunt mai mici de 1, punctele fiind pe sfera unitate. • Cum distanţele dintre puncte sunt invers proporţionale cu corelaţiile dintre variabilele corespunzătoare, grupările de puncte indică grupuri de variabile corelate. • Pentru eliminarea erorilor de perspectivă, aprecierea corectă apare doar după analiza proiecţiilor pe mai multe planuri factoriale (= nr. de factori – 1). • Variabilele apropiate de o axă sunt corelate cu acea componentă principală, se poate considera că axa respectivă este o combinaţie a variabilelor apropiate de ea. 05 -Nov-20 10

Reprezentări grafice • Reprezentarea punctelor-observaţii prezintă de asemenea grupările de observaţii, fără a mai fi pe sfera unitate. • Prima axă factorială este, uzual, factorul de talie, separând de-a lungul ei observaţiile mici de cel mari. • A doua axă factorială este factorul de formă, care nuanţează diferenţele evidenţiate de primul factor. • Dacă observaţiile aparţin la grupuri de interes, evidenţierea claselor (ca în figură) poate oferi informaţii utile prin configuraţiile vizibile. • Concluziile sunt justificate doar după utilizarea unui număr suficient de proiecţii. 05 -Nov-20 F 1 11

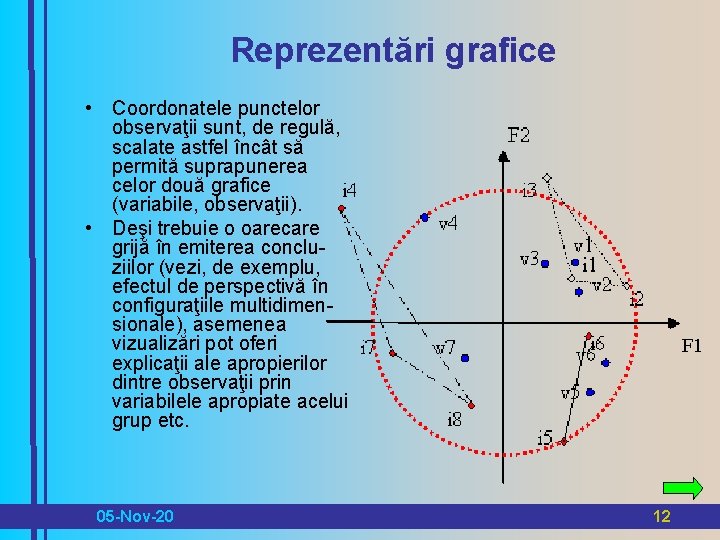
Reprezentări grafice • Coordonatele punctelor observaţii sunt, de regulă, scalate astfel încât să permită suprapunerea celor două grafice (variabile, observaţii). • Deşi trebuie o oarecare grijă în emiterea concluziilor (vezi, de exemplu, efectul de perspectivă în configuraţiile multidimensionale), asemenea vizualizări pot oferi explicaţii ale apropierilor dintre observaţii prin variabilele apropiate acelui grup etc. 05 -Nov-20 F 1 12

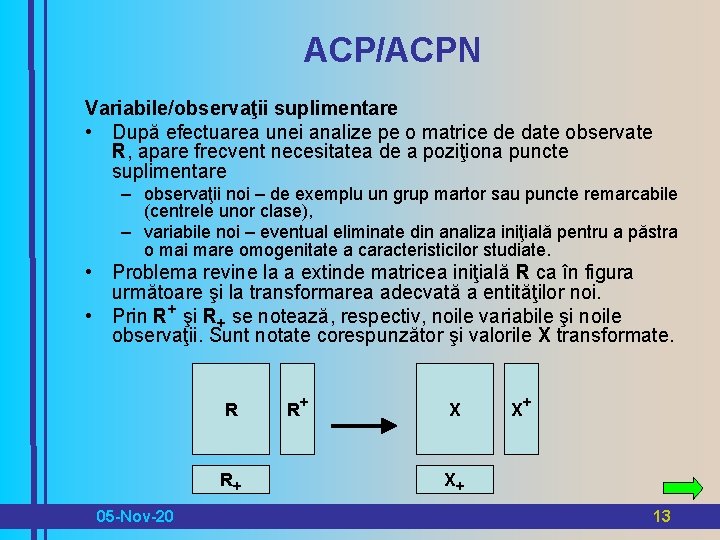
ACP/ACPN Variabile/observaţii suplimentare • După efectuarea unei analize pe o matrice de date observate R, apare frecvent necesitatea de a poziţiona puncte suplimentare – observaţii noi – de exemplu un grup martor sau puncte remarcabile (centrele unor clase), – variabile noi – eventual eliminate din analiza iniţială pentru a păstra o mai mare omogenitate a caracteristicilor studiate. • Problema revine la a extinde matricea iniţială R ca în figura următoare şi la transformarea adecvată a entităţilor noi. • Prin R+ şi R+ se notează, respectiv, noile variabile şi noile observaţii. Sunt notate corespunzător şi valorile X transformate. R R+ 05 -Nov-20 R+ X X+ X+ 13

ACP/ACPN Puncte-variabile suplimentare • Variabilele noi din R+ sunt făcute comparabile cu variabilele analizate prin centrare şi reducere (tabloul X+), ceea ce va duce punctele respective pe sfera unitară din R n. • Coordonatele punctelor, corespunzătoare axei , se obţin proiecţie, deci calculând produsul scalar cu vectorul unitar v : 05 -Nov-20 14

ACP/ACPN Puncte-observaţii suplimentare • Noile puncte sunt făcute comparabile cu liniile iniţiale prin raportarea la centrul de gravitate al norului iniţial şi reducerea utilizând abaterile standard ale variabilelor iniţiale. • Coordonatele noilor puncte pe axa sunt, prin proiecţie, vectorul produselor scalare cu versorul axei, u , în R p 05 -Nov-20 15

Analiza corespondenţelor • Dintre metodele factoriale, analiza corespondenţelor este dedicată, în special, tablourilor de contingenţă. • Presupunem că într-un studiu statistic s-au considerat două variabile discrete. Dispunem, deci, de tabloul (kij), unde kij este frecvenţa observaţiilor care s-au încadrat în categoria i după prima variabilă şi în categoria j după a doua variabilă. • Într-un asemenea tablou, liniile şi coloanele reprezintă două partiţii ale aceleeaşi populaţii şi joacă, prin urmare, roluri identice (ceea ce nu se întâmpla la analiza în componente principale). • Se poate considera, mai general, că se pleacă de la un tablou (kij) de numere nenegative, dar în continuare se presupune cazul unui tablou de frecvenţe. 05 -Nov-20 16

Analiza corespondenţelor • Pentru a putea atribui un sens distanţei dintre punctele-linii şi punctele-coloane, este necesar să se treacă la frecvenţele relative, obţinându-se astfel “profile” de linii, respectiv de coloane, prin transformările uzuale din statistica descriptivă. • Fixând dimensiunea tabloului la n p definim: kij efectivul unei celule, efectivul total, fij = kij / k frecvenţa relativă a unei celule, frecvenţele relative marginale, fij / fi , j = 1, 2, …, p, profilul liniei i, fij / f j , i = 1, 2, …, n, profilul coloanei j. 05 -Nov-20 17

Analiza corespondenţelor Norii de puncte • În R p avem n puncte, având coordonatele { fij / fi • , j = 1, 2, …, p}, i = 1, 2, …, n şi se consideră că fiecare punct i are o masă fi • . • Cum suma coordonatelor unui punct este egală cu 1, aceste puncte sunt situate într-un subspaţiu cu p– 1 dimensiuni. • Apropierile dintre puncte se interpretează ca apropieri între profilele-linii, deci apropieri între categoriile variabilei corespunzătoare. • În R n avem p puncte, fiecare cu coordonatele { fij / f • j , i = 1, 2, …, n}, j = 1, 2, …, p şi având o masă f • j. Acest nor de puncte este situat într-un subspaţiu cu n– 1 dimensiuni. 05 -Nov-20 18

Analiza corespondenţelor • Ca distanţă între două puncte se alege distanţa 2, adică: – între linii – între coloane 05 -Nov-20 19

Analiza corespondenţelor • Distanţa 2 are proprietatea de a verifica principiul de “echivalenţă distribuţională”: Dacă două puncte-linii, i 1 şi i 2, sunt confundate şi se consideră drept un nou punct de masă egală cu suma maselor celor două puncte (i 1 şi i 2 sunt înlocuite cu i 0), atunci distanţele dintre toate punctele din R n şi R p rămân neschimbate. • Proprietatea este verificată şi pentru punctele coloane. • Această proprietate poate avea un rol stabilizator asupra rezultatelor prin aceea că agregarea unor profile vecine (pe linii sau coloane) nu modifică substanţial rezultatele obţinute. 05 -Nov-20 20

Analiza corespondenţelor Invarianţa distanţelor în R p • Dacă punctele i 1 şi i 2 sunt confundate în R p are loc, pentru orice j de unde dar numitorii sunt egali şi deci • Prin urmare calculele f*j = fij nu sunt afectate, distanţele d 2(i, i ’) se păstrează. 05 -Nov-20 21

Analiza corespondenţelor Analiza în R p • Distanţa 2 nu este euclidiană şi prin urmare nu se poate aplica direct analiza generală. • Se modifică, de aceea, scala axelor prin aceea că se normează coordonatele prin împărţire cu • Noile coordonate ale unui punct i vor fi 05 -Nov-20 22

Analiza corespondenţelor • Distanţa euclidiană uzuală dintre punctele i şi i’ este şi se verifică simplu că această distanţă coincide cu distanţa 2 definită iniţial. • Se ajunge astfel la cazul analizei generale, considerându-se norul de puncte având coordonatele precizate. 05 -Nov-20 23

Analiza corespondenţelor • Norul de puncte este acum în hiperplanul de ecuaţie deoarece coordonatele unui punct verifică ecuaţia precedentă: • Trebuie să se determine prima componentă principală a acestui nor de puncte (interesându-ne forma norului şi nu poziţia faţă de origine). 05 -Nov-20 24

Analiza corespondenţelor • Se introduce centrul de greutate al norului de puncte, notat cu G, având coordonatele (fiecare punct i având masa fi*) • După translaţia originii în punctul G, coordonatele punctului i devin punctul păstrând, în continuare, masa 05 -Nov-20 . 25

Analiza corespondenţelor 05 -Nov-20 26

Analiza corespondenţelor • Se arată că vectorul up cu componentele (f*j)1/2 este vector propriu pentru X’X, la valoarea proprie 0. • Din ortogonalitatea vectorilor proprii rezultă atunci că orice alt vector propriu u verifică • De aici va rezulta (aproape imediat) că, numeric, analiza se poate realiza şi pe matricea necentrată X* dacă se elimină vectorul propriu up relativ la valoarea proprie 1. • Matricea X* are elementele date de 05 -Nov-20 27

Analiza corespondenţelor • După determinarea axelor factoriale, prin metoda generală, coordonata punctului i pe axa este dată de care se poate simplifica la • Aceste coordonate pot fi utilizate pentru realizarea proiecţiilor pe planele factoriale pentru a identifica structura norului de puncte. 05 -Nov-20 28

Analiza corespondenţelor 05 -Nov-20 29

Analiza corespondenţelor Relaţia dintre spaţiile R p şi R n • Potrivit analizei generale se arată că • Formulele devin, în cazul analizei corespondenţelor, legătura dintre coordonatele punctelor linii şi cele ale punctelor coloane implicând matricele de profiluri. 05 -Nov-20 30

Analiza corespondenţelor Reconstituirea tabloului de frecvenţe • Potrivit metodei generale, • Utilizând formulele anterioare care dau pe v şi u , se obţine pentru x*ij de unde, ştiind prima valoare proprie (=1) şi vectorii proprii corespunzători 05 -Nov-20 31

Analiza corespondenţelor Contribuţii absolute şi relative • Pentru a interpreta axele determinate într-o analiză a corespondenţelor se calculează două serii de coeficienţi pentru fiecare dintre elementele celor două mulţimi (puncte-linii şi puncte-coloane, pe de o parte, factori pe de altă parte) puse în corespondenţă. – contribuţii absolute — exprimă partea asumată de un element dat în varianţa “explicată” de un factor; – contribuţii relative (corelaţia element-factor) — exprimă partea asumată de un factor în “explicarea” varianţei unui element. • Contribuţiile absolute evidenţiază punctele (variabilele) “responsabile” de construcţia unui factor, iar contribuţiile relative arată punctele (variabilele) preponderente într-un factor. 05 -Nov-20 32

Analiza corespondenţelor Contribuţii absolute • Calculând varianţa coordonatelor celor n puncte-linie i pe axa , fiecare fiind ponderat cu masa sa, se obţine: • De reamintit că suma valorilor proprii reprezintă varianţa globală. • Analog, pentru cele p puncte-coloană, varianţa coordonatelor pe axa este • Se definesc atunci contribuţiile absolute ale elementelor i şi, respectiv, j la axa : 05 -Nov-20 33

Analiza corespondenţelor Contribuţii relative • Axele factoriale din fiecare subspaţiu constituie un reper ortonormat. Pătratul distanţei unui punct la centrul de gravitaţie (G sau H, originile subspaţiului respectiv) se descompune astfel în suma pătratelor coordonatelor. • Câtul este deci pătratul cosinusului unghiului punctului i cu axa , ceea ce reprezintă un coeficient de determinare (pătratul unui coeficient de corelaţie). Cantitatea Cr (i) se numeşte contribuţia relativă a factorului la poziţionarea punctului i. 05 -Nov-20 34

Analiza corespondenţelor • Se defineşte în mod similar contribuţia relativă a factorului la poziţia punctului-coloană j • Se arată imediat, din descompunerea distanţelor, că relaţii care vin în sprijinul denumirii de contribuţii relative. • Contribuţiile cele mai mari vor indica punctele (grupările de puncte) care determină axele factoriale. 05 -Nov-20 35

Alte concepte • Încărcările factorului (factor loadings, indici de saturare) sunt coeficienţii de corelaţie dintre variabile şi factor. – Pătratul acestuia exprimă procentul din varianţa variabilei explicată de factor. – Pentru a obţine procentajul de varianţă explicată în toate variabilele de un factor se adună pătratele încărcărilor pentru factor şi se împarte la numărul variabilelor (acelaşi rezultat ca şi împărţirea valorii proprii corespunzătoare factorului la numărul de variabile). • Numim comunalitate (communality) a unei variabile observate pătratul coeficientului de corelaţie dintre variabila respectivă şi partea explicată de factori (pătratul coeficientului de corelaţie multiplă folosind factorii ca variabile independente). – Poate fi calculată ca suma pătratelor încărcărilor tuturor factorilor, corespunzătoare variabilei. Prin urmare, comunalitatea exprimă proporţia din varianţa variabilei explicată de factorii comuni. Deoarece această proporţie creşte o dată cu mărirea numărului de factori consideraţi, ea nu constituie un criteriu de alegere a numărului de factori. – Comunalităţi mici, pe de altă parte, sunt interpretate mai degrabă ca o evidenţă a faptului că variabilele analizate au puţine lucruri în comun cu celelalte variabile. 05 -Nov-20 36

Tipuri de factori • Se pot identifica: – factori generali: obţinuţi din toate sau din marea majoritate a variabilelor, exprimă o “parte comună” tuturor variabilelor; – factori de grup: obţinuţi doar dintr-un grup de variabile, restul variabilelor au coeficienţi neglijabili; – factori unici: obţinuţi doar dintr-o variabilă, exprimă faptul că variabila respectivă explică o parte comună a celorlalte variabile. 05 -Nov-20 37

Rotaţia factorilor • • Prin rotaţia factorilor se înţelege o transformare a sistemului de coordonate în spaţiul factorilor, astfel încât să se obţină un “unghi de vedere” mai bun. De exemplu, o axă factorială este mai uşor de interpretat dacă trece printr-o grupare de puncte. Există două categorii de rotaţii: – ortogonale: factorii rămân necorelaţi şi se incearcă doar o repoziţionare a sistemului de coordonate; – oblice: factorii devin corelaţi (nu mai sunt ortogonali), dar se obţine o mai bună “trecere” a axelor prin grupările de puncte. • Dintre rotaţiile ortogonale, mai utilizate sunt: • – VARIMAX – “simplifică factorii” prin maximizarea varianţei încărcărilor variabilelor după un factor; tinde să producă factori de grup. – QUARTIMAX – “simplifică variabilele” prin maximizarea varianţei încărcărilor unei variabile după factori; tinde să producă factori generali sau de grupuri mici. Dintre rotaţiile oblice, metoda mai utilizată este PROMAX care relaxează restricţiile de ortogonalitate pentru ca factorii să treacă mai bine prin grupările de puncte. De regulă, orice rotaţie oblică are un parametru care fixează corelaţia maximă permisă între doi factori. 05 -Nov-20 38

Validitatea rezultatelor • În această secţiune se propune un răspuns la întrebarea: Sunt stabile configuraţiile identificate în urma reducerii dimensiunii problemei şi analizării proiecţiilor? • Un răspuns poate fi obţinut prin perturbarea tabloului de date simulând fluctuaţii (erori de măsurare). Repetând analiza pentru noile date, se poate observa care sunt asociaţiile stabile şi începând cu ce rang sunt perturbate axele factoriale. Se obţin astfel configuraţiile asupra cărora trebuie să se îndrepte interpretarea, ca şi dimensiunea subspaţiului de reprezentare. • Perturbaţiile simulate pot fi: – generarea de erori de măsurare pseudo aleatoare, cu distribuţii specifice datelor (normale, uniforme etc. ), pentru a vedea efectul preciziei măsurătorilor asupra rezultatelor; – schimbări monotone ale variabilelor ordinale, pentru a evidenţia partea din reprezentări care depinde doar de ordinea valorilor şi nu de scalele sau codificările utilizate; – formarea aleatorie de eşantioane (de linii sau de coloane), pentru a vedea o eventuală invarianţă în raport cu sondajul. 05 -Nov-20 39
 Paired t test vs unpaired
Paired t test vs unpaired Titik pelana adalah
Titik pelana adalah Univariat multivariat
Univariat multivariat Fungsi lagrange
Fungsi lagrange Psychologie
Psychologie Peralatan manajemen baru
Peralatan manajemen baru Multivariat analys
Multivariat analys Analisa multivariat adalah
Analisa multivariat adalah Multivariat analyse
Multivariat analyse Kovariansi
Kovariansi Valentin stefanescu
Valentin stefanescu Sobre la mesa de mármol había un hermoso joyero de nácar
Sobre la mesa de mármol había un hermoso joyero de nácar Thomas taylor forensic science
Thomas taylor forensic science Diaporama pour la st valentin
Diaporama pour la st valentin Valentin ventura
Valentin ventura Valentin abe
Valentin abe Boris polishchuk
Boris polishchuk Mia valentin
Mia valentin Legenda o valentinovu
Legenda o valentinovu Oš valentin klarin
Oš valentin klarin Valentin vydrin
Valentin vydrin Dominique valentin
Dominique valentin Hr valentin gomez farias
Hr valentin gomez farias Valentin ross forensic science
Valentin ross forensic science Valentin coirier
Valentin coirier New age wine calories
New age wine calories Valentin peretroukhin
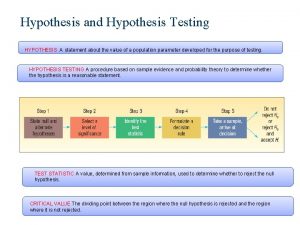
Valentin peretroukhin Hypothesis testing examples and solutions doc
Hypothesis testing examples and solutions doc How to find p value from t statistic
How to find p value from t statistic Statistic
Statistic Test statistic
Test statistic Homoskedasticity-only f-statistic
Homoskedasticity-only f-statistic Confidence interval with margin of error
Confidence interval with margin of error Functions of statistics
Functions of statistics Types of hook in an essay
Types of hook in an essay What is this called
What is this called Test statistic for single proportion
Test statistic for single proportion What is statistic
What is statistic Holmes statistic summary
Holmes statistic summary F test statistic formula
F test statistic formula