Statistic multivariat prezentat de Valentin Clocotici Noiuni introductive

Statistică multivariată prezentată de Valentin Clocotici

Noţiuni introductive (recapitulare - 2) Cursul nr. 2 05 -Nov-20 2

Elemente de teoria probabilităţilor • • • Teoria probabilităţilor este introdusă ca teoria matematică a fenomenelor aleatorii. Prin fenomen aleatoriu înţelegem un fenomen a cărui apariţie este sub semnul hazardului, a întâmplării. Noţiunea contrară este aceea de fenomen determinat, adică fenomen a cărui apariţie este previzibilă prin cunoaşterea cauzalităţii sale. Uneori, caracterul de aleatoriu este dat doar de necunoaşterea cauzei implicate, dacă există o asemenea cauză. Noţiunile de bază în teoria probabilităţilor sunt proba şi evenimentele asociate probei. Probă şi eveniment sunt concepte fundamentale teoriei probabilităţilor, drept urmare nu sunt definite în funcţie de alte noţiuni. Ele idealizează, abstractizează, noţiunile de “experienţă”, “cercetare”, “investigaţie” şi, respectiv, “rezultatele” observate în cercetare. De remarcat, totuşi, faptul că evenimentele sunt dintr‑o mulţime fixată. Vom nota, în continuare, mulţimea evenimentelor cu A iar evenimentele cu litere mari: A, B, C etc. În cazul finit reamintim că A = P( ), unde este mulţimea evenimentelor elementare. Între evenimente se definesc operaţii, inspirate din teoria mulţimilor: Egalitatea, Negaţia, Reuniunea, Intersecţia, Incluziunea. 05 -Nov-20 3

Elemente de teoria probabilităţilor • În mulţimea evenimentelor se disting două eveni mente cu caracter special: – evenimentul sigur este evenimentul care se produce cu certitudine; se notează cu . De exemplu, evenimentul “cap sau pajură” la aruncarea unei monede este un eveniment sigur. – evenimentul imposibil este evenimentul care nu se produce niciodată; se notează cu . Este evident că evenimentul sigur este evenimentul contrar evenimentului imposibil şi reciproc. • Se poate astfel spune că evenimentele sunt de trei categorii: sigure, imposibile şi aleatorii. • Două evenimente A şi B se spun incompatibile dacă intersecţia lor este evenimentul imposibil, A B = , adică nu este posibil ca evenimentele A şi B să se producă simultan. 05 -Nov-20 4

Elemente de teoria probabilităţilor • În prezentarea şi prelucrarea datelor, măsurate pe diverse scale, noţiunea de frecvenţă relativă este o noţiune unificatoare: se regăseşte la toate scalele, valorile obţinute pot fi utilizate pentru comparaţii etc. Practica arată că atunci când o experienţă este repetată de un număr mare de ori, frecvenţa relativă a apariţiei unui fapt tinde să se stabilizeze. • Acest fenomen este formalizat în teoria probabilităţilor prin introducerea noţiunii de probabilitate. • Fie A mulţimea evenimentelor. Se numeşte probabilitate orice funcţie cu valori reale definită pe mulţimea evenimentelor, P : A , şi care satisface: – probabilitatea oricărui eveniment este un număr nenegativ: P(A) 0; – probabilitatea evenimentului sigur este egală cu 1: P( ) = 1; – probabilitatea oricărei reuniuni de evenimente incompatibile două câte două este egală cu suma probabilităţilor evenimentelor. 05 -Nov-20 5

Elemente de teoria probabilităţilor • Se poate deduce din definiţia anterioară că, dată o mulţime de bază şi o mulţime de evenimente, se pot defini mai multe funcţii de probabilitate. Însă, odată definită funcţia de probabilitate, toate rezultatele dezvoltate pentru probă vor fi determinate de această alegere. • Se spune că tripleta ( , A, P) defineşte un spaţiu de probabilitate. • Se numeşte probabilitatea evenimentului A condiţionată de evenimentul B valoarea notată P(A | B) şi definită prin : unde P(B) este diferită de 0. Altfel spus, P(A|B) reprezintă probabilitatea evenimentului A ştiind că s‑a realizat B. Evenimentele A şi B se zic independente dacă are loc P(A | B) = P(A)P(B). 05 -Nov-20 6

Elemente de teoria probabilităţilor • Cu ajutorul variabilelor aleatoare se modelează în teoria probabilităţilor ceea ce în ştiinţele experimen tale este prin caracteristică, variabilă studiată etc. • Faptul poate fi intuit corect dacă se consideră, de exemplu, măsurarea înălţimii unui elev într‑o cercetare antropometrică. – A spune că elevul X are înălţimea de 1, 20 m trebuie înţeles că mai întâi a fost selectat elevul X (realizarea unui eveniment) şi apoi că operaţiunea de măsurare a avut ca rezultat valoarea de 1, 20 m (o valoare a fost atribuită evenimentului). Observaţie. Se reaminteşte definirea variabilelor aleatoare şi a noţiunilor conexe doar pentru cazul general, fără a prezenta separat cazul finit; noţiunile specifice cazului finit vor fi amintite doar acolo unde apar. 05 -Nov-20 7

Elemente de teoria probabilităţilor • Fie un spaţiu de probabilitate ( , A, P). Se numeşte variabilă aleatoare o funcţie reală X: , care satisface condiţia: • Cu alte cuvinte se cere, din considerente teoretice, ca mulţimea evenimentelor elementare pentru care v. a. X are valori mai mici sau egale cu x, oricare ar fi x, să fie tot un eveniment. Definiţia din cazul finit nu poate fi aplicată aici deoarece împărţirea probabilităţii totale la un număr (potenţial) infinit de evenimente elementare produce o probabilitate egală cu zero pentru fiecare eveniment în parte. In cazul infinit, are sens să considerăm probabilitatea ca v. a. X să aparţină la un anumit interval şi nu probabilitatea să ia o anumită valoare. • • – Acest fapt nu este chiar atât de depărtată de practica experimentală întrucât, de exemplu, şansa de a găsi un individ cu înălţimea de 1, 80 m este aproape nulă dacă măsurarea se efectuează cu eroare zero. De obicei printr‑o asemenea valoare înţelegem un întreg interval de înălţimi, toate acelea care prin rotunjire la două zecimale devin 1, 80 m. 05 -Nov-20 8

Elemente de teoria probabilităţilor • Numim funcţie de repartiţie a v. a. X, funcţia reală de variabilă reală, F: , definită prin unde prin (X x) s‑a notat evenimentul adică reuniunea acelor evenimente elementare pentru care v. a. ia valori mai mici sau egale cu x. • Funcţia de repartiţie se zice absolut continuă dacă există o funcţie reală, f : , astfel încât 05 -Nov-20 9

Elemente de teoria probabilităţilor • Interpretarea geometrică este cea uzuală de mărime a ariei de sub graficul funcţiei f. f F(x) x X • Funcţia f, dacă există, se numeşte densitate de probabilitate a v. a. X şi are proprietăţile 05 -Nov-20 10

Elemente de teoria probabilităţilor Proprietăţile definitorii ale funcţiei de repartiţie sunt: 1. 2. Funcţia F este nedescrescătoare (dacă atunci 3. Dacă F este funcţie de repartiţie absolut continuă a v. a. X, atunci are loc şi proprietatea: formulă care permite calculul probabilităţilor atunci când se cunoaşte funcţia de repartiţie. Funcţia de repartiţie conţine toată informaţia necesară pentru calcularea probabilităţilor cu care o variabilă aleatoare ia valori şi pentru acest lucru va fi utilizată în ceea ce ne interesează. 05 -Nov-20 11

Elemente de teoria probabilităţilor • Pentru caracterizarea unei v. a. se definesc valori tipice, care reprezintă (modelează) rezumatele statistice ale variabilelor. • Formulele de calcul (nu sunt toate reamintite aici) sunt diferite în cazul finit faţă de cazul infinit. • Valorile tipice sintetizează – gruparea valorilor: valoarea mod, mediana, media aritmetică; – împrăştierea valorilor: quantile, momente centrate, abaterea standard, coeficient de variaţie; – atribute ale reprezentării grafice: coeficientul de aplatizare, coeficientul de asimetrie. • De exemplu, formulele de calcul pentru medie, , sunt – cazul discret – cazul infinit 05 -Nov-20 12

Elemente de teoria probabilităţilor • Pentru aprecierea gradului de simetrie a unei repartiţii se utilizează momentul centrat de ordinul al treilea, 3, care ponderează suplimentar valorile mai depărtate de medie dar conservă şi semnul abaterii de la medie. Rezultă că valori negative ale momentului centrat de ordinul 3 reflectă repartiţii asimetrice spre stânga iar valori pozitive reflectă repartiţii asimetrice spre dreapta. • Coeficientul de asimetrie este definit prin standardizarea momentului 3, necesară pentru a i oferi putere de comparare: unde 2 este dispersia. • Simetria unei repartiţii se reflectă în forma simetrică a graficu lui densităţii de probabilitate sau a funcţiei de probabilitate. • Se poate considera că indicatorul se referă la forma graficului densităţii (funcţiei) de probabilitate. 05 -Nov-20 13

Elemente de teoria probabilităţilor • Al doilea atribut important (primul fiind simetria) în aprecierea formei unei repartiţii unimodale este gradul de înălţare în apropierea valorii mod. • Acest fapt poate fi măsurat prin panta curbei densităţii de probabilitate şi este definit drept coeficient de boltire (sau coeficient de aplatizare). • Se observă forma standardizată a acestui coeficient ceea ce permite utilizarea lui în comparaţii între variabile aleatoare. • O valoare mai mare a coeficientului de boltire arată o supraînălţare în apropierea valorii mod, deci reflectă faptul că valorile respective au probabilităţi de realizare mult mai mari decât valorile mai depărtate. 05 -Nov-20 14

Elemente de teoria probabilităţilor • Utilizarea coeficientului este realizată uneori prin raportare la boltirea repartiţiei normale boltire egală cu 3. Se introduce astfel excesul unei v. a. X prin E = b 2 3 • În funcţie de valoarea excesului, repartiţia este numită: – platicurtică, dacă E < 0 (sau b 2 < 3); – mezocurtică, dacă E = 0 (sau b 2 = 3); – leptocurtică, dacă E > 0 (sau b 2 > 3). 05 -Nov-20 15

Elemente de teoria probabilităţilor • În continuare se prezintă câteva dintre repartiţiile teoretice care sunt utilizate în analiza datelor experimentale. • Trebuie avut în vedere faptul că utilizarea unui model teoretic nu rezolvă toate problemele experimentale. • De multe ori, fenomenul real este modelat cu un grad scăzut de aproximare, astfel încât rezultatele obţinute sunt doar orientative. • Acest fapt reflectă doar limitele cunoaşterii şi nu, poate, faptul că o modelare nu este posibilă în domeniul studiat. • De cele mai multe ori, însă, nici nu există alternativă de prelucrare, astfel încât, chiar orientative, rezultatele sunt utile. 05 -Nov-20 16

Repartiţia normală • Această repartiţie are un rol central, atât din considerente teoretice, cât şi practice (nu în ultimul rând, uşurinţa aplicării). • Teoretic, repartiţia normală reprezintă o repartiţie limită către care tind, în anumite condiţii, celelalte repartiţii. • Practic, atunci când nu se cunoaşte repartiţia unui anumit fenomen, se poate considera, cu respectarea unui număr minim de condiţii, că fenomenul urmează o repartiţie normală. • Prin definiţie, o variabilă continuă X are o repartiţie normală, sau repartiţie Gauss–Laplace, dacă funcţia de repartiţie este dată de: unde şi sunt parametrii funcţiei de repartiţie • Funcţia de repartiţie normală se va nota prin N( ; 2) iar faptul că v. a. X este repartizată normal cu parametrii şi se notează X ~ N( ; 2). 05 -Nov-20 17

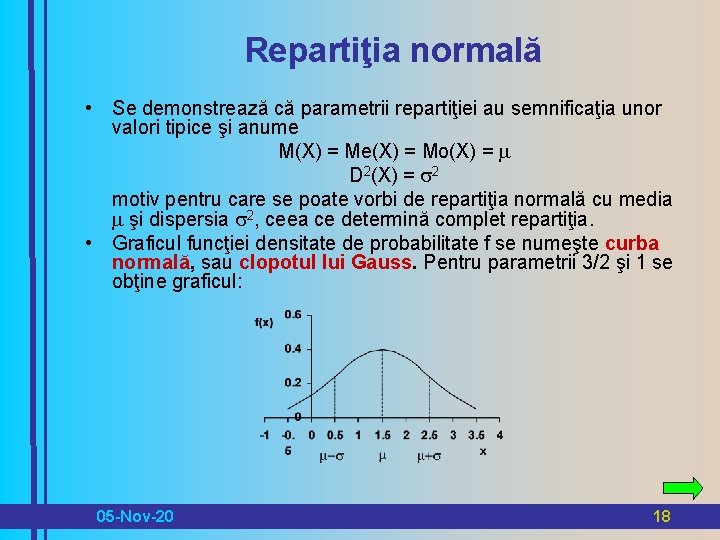
Repartiţia normală • Se demonstrează că parametrii repartiţiei au semnificaţia unor valori tipice şi anume M(X) = Me(X) = Mo(X) = D 2(X) = 2 motiv pentru care se poate vorbi de repartiţia normală cu media şi dispersia 2, ceea ce determină complet repartiţia. • Graficul funcţiei densitate de probabilitate f se numeşte curba normală, sau clopotul lui Gauss. Pentru parametrii 3/2 şi 1 se obţine graficul: 05 -Nov-20 18

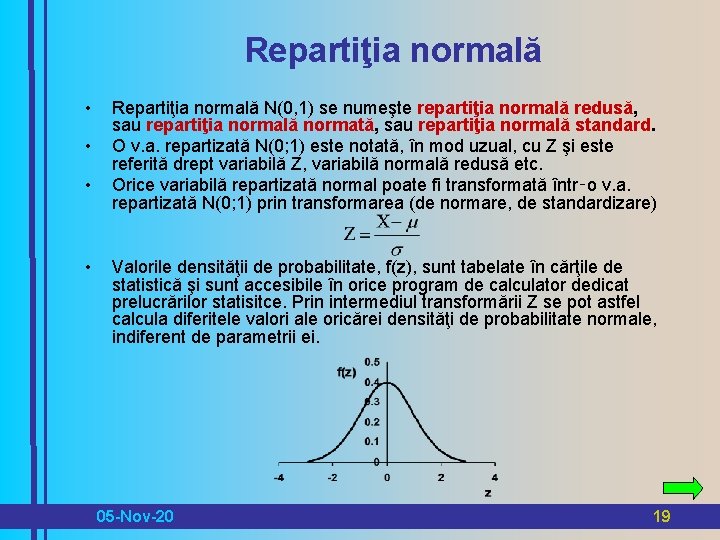
Repartiţia normală • • Repartiţia normală N(0, 1) se numeşte repartiţia normală redusă, sau repartiţia normală normată, sau repartiţia normală standard. O v. a. repartizată N(0; 1) este notată, în mod uzual, cu Z şi este referită drept variabilă Z, variabilă normală redusă etc. Orice variabilă repartizată normal poate fi transformată într‑o v. a. repartizată N(0; 1) prin transformarea (de normare, de standardizare) Valorile densităţii de probabilitate, f(z), sunt tabelate în cărţile de statistică şi sunt accesibile în orice program de calculator dedicat prelucrărilor statisitce. Prin intermediul transformării Z se pot astfel calcula diferitele valori ale oricărei densităţi de probabilitate normale, indiferent de parametrii ei. 05 -Nov-20 19

Repartiţia normală • Notând cu z quantila de ordin a repartiţiei N(0, 1), reamintim că = F(z ) = P(Z < z ) • În aplicaţii sunt utile următoarele relaţii pentru o variabila aleatoare X oarecare, repartizată normal, N( , 2): – calculul probabilităţii pentru o v. a. X oarecare, – calculul probabilităţii ca o v. a. X să ia valori între două valori date unde z 1 şi z 2 sunt transformatele Z ale valorilor x 1 şi x 2. 05 -Nov-20 20

Repartiţia normală • Calculul probabilităţilor ca o v. a. X să ia valori raportate la medie şi abatere standard unde k este o constantă pozitivă • Ultima relaţie este utilă prin aceea că exprimă probabilitatea cu care valorile v. a. X se abat de la medie cu mai puţin de k abateri standard. Cantitatea 2 F(k)– 1, exprimată eventual procentual, este numită uneori siguranţă statistică. Poate fi interpretată ca o măsură a încrederii în faptul că v. a. X ia valori în intervalul menţionat. 05 -Nov-20 21

Repartiţia c 2 • Cunoscută, sub influenţa literaturii în limba engleză şi a programelor de calculator, şi sub numele de repartiţia CHI‑ 2, repartiţia c 2 este utilizată mai mult în testarea ipotezelor statistice decât ca model statistic. Din acest motiv vom defini repartiţia c 2 drept repartiţia unei v. a. care se obţine ca suma pătratelor unor v. a. independente repartizate normal standard, adică: dacă Z 1, Z 2, …, Zn sunt variabile aleatoare independente, fiecare cu repartiţia N(0; 1), atunci variabila aleatoare o repartiţie c 2 cu n grade de libertate. • Singurul parametru al repartiţiei c 2 este numărul gradelor de libertate. În general, prin numărul gradelor de libertate asociate unei entităţi se înţelege numărul variabilelor independente a căror variaţie nu suferă nici o restricţie şi care definesc mărimea considerată. 05 -Nov-20 22

Repartiţia c 2 • Principalii indicatori statistici sunt • Notăm quantila de ordin v. a. c 2 prin . • Deoarece nu există ramura negativă a repartiţiei se obişnuieşte să se noteze quantilele într un mod inversat, adică Graficul este o curbă descrescătoare pentru n = 1 sau n = 2, iar pentru n > 2 are un punct de maxim în punctul de abscisă x = n�– 2. 05 -Nov-20 23

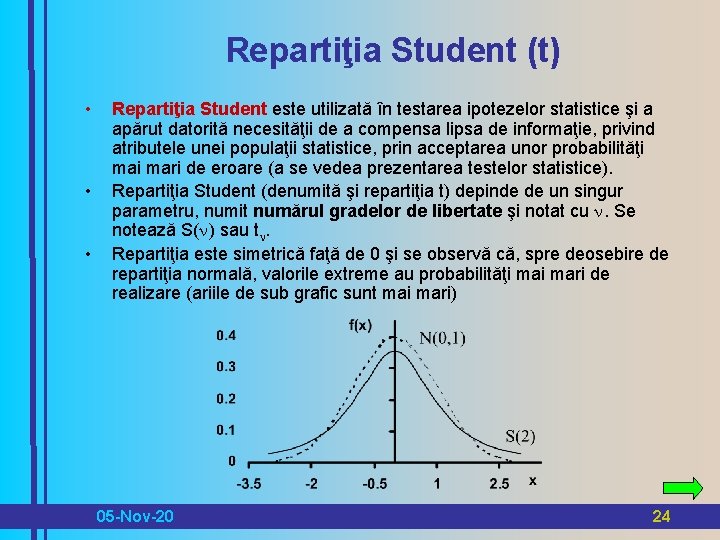
Repartiţia Student (t) • • • Repartiţia Student este utilizată în testarea ipotezelor statistice şi a apărut datorită necesităţii de a compensa lipsa de informaţie, privind atributele unei populaţii statistice, prin acceptarea unor probabilităţi mari de eroare (a se vedea prezentarea testelor statistice). Repartiţia Student (denumită şi repartiţia t) depinde de un singur parametru, numit numărul gradelor de libertate şi notat cu n. Se notează S(n) sau tn. Repartiţia este simetrică faţă de 0 şi se observă că, spre deosebire de repartiţia normală, valorile extreme au probabilităţi mari de realizare (ariile de sub grafic sunt mai mari) 05 -Nov-20 24

Repartiţia Student (t) • Dintre rezultatele importante care privesc repartiţia t menţionăm: – Dacă X este repartizată normal standard, X~N(0; 1), iar Y este repartizată c 2 cu n grade de libertate, Y ~ c 2 n, atunci v. a. Z obţinută prin este repartizată Student cu n grade de libertate. 05 -Nov-20 25

Repartiţia Student (t) • Indicatorii statistici principali ai unei v. a. t ~ tn sunt M(t) = 0 D 2(t) = pentru n > 2. • Dacă n > 30, atunci D 2(t) devine aproximativ egal cu 1 iar densitatea de probabilitate se apropie foarte mult de aceea a unei v. a. normale reduse. Acest fapt permite ca, pentru aplicaţiile practice, repartiţia Student cu mai mult de 30 de grade de libertate să fie aproximată cu o repartiţie N(0; 1). • Quantilele distribuţiei se notează cu ta; n, adică valorile pentru care 05 -Nov-20 26

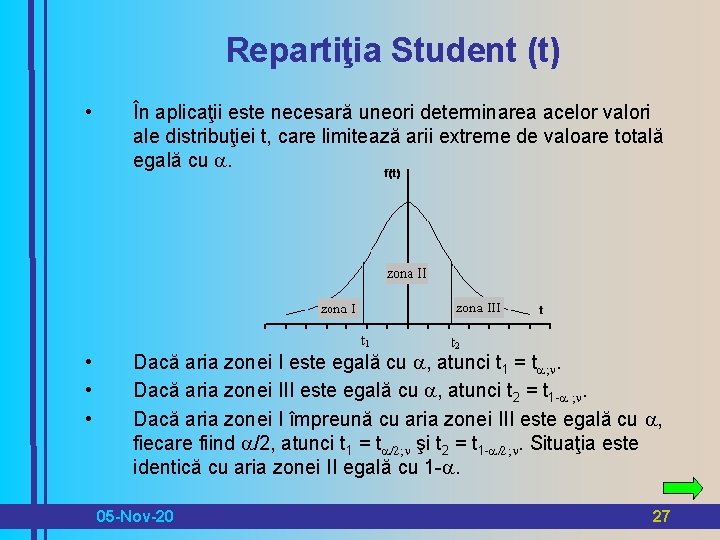
Repartiţia Student (t) • În aplicaţii este necesară uneori determinarea acelor valori ale distribuţiei t, care limitează arii extreme de valoare totală egală cu . • • • Dacă aria zonei I este egală cu , atunci t 1 = t ; n. Dacă aria zonei III este egală cu , atunci t 2 = t 1 ; n. Dacă aria zonei I împreună cu aria zonei III este egală cu , fiecare fiind /2, atunci t 1 = t /2; n şi t 2 = t 1 /2; n. Situaţia este identică cu aria zonei II egală cu 1 . 05 -Nov-20 27

Repartiţia Fisher-Snedecor (F) • Repartiţia F este introdusă ca o repartiţie utilă în testarea ipotezelor statistice privind compararea a două dispersii. • Repartiţia F depinde de doi parametri, n 1 şi n 2, ambii având semnificaţia unor grade de libertate. • Notaţia uzuală este F(n 1, n 2) sau Fn 1; n 2. • Dacă repartiţia se referă la o variabilă aleatoare care se obţine drept câtul altor două v. a. , atunci n 1 este numărul gradelor de libertate pentru numărător şi n 2 este numărul gradelor de libertate pentru numitor. 05 -Nov-20 28

Repartiţia Fisher-Snedecor (F) • Dintre rezultatele importante legate de repartiţia F menţionăm teorema, luată uneori ca definiţie pentru o v. a. repartizată Fisher– Snedecor: – Dacă Y 1 şi Y 2 sunt două variabile aleatoare independente repartizate c 2, cu n 1 şi, respectiv, n 2 grade de libertate, atunci v. a. X definită prin are o repartiţie F cu n 1 şi n 2 grade de libertate. 05 -Nov-20 29

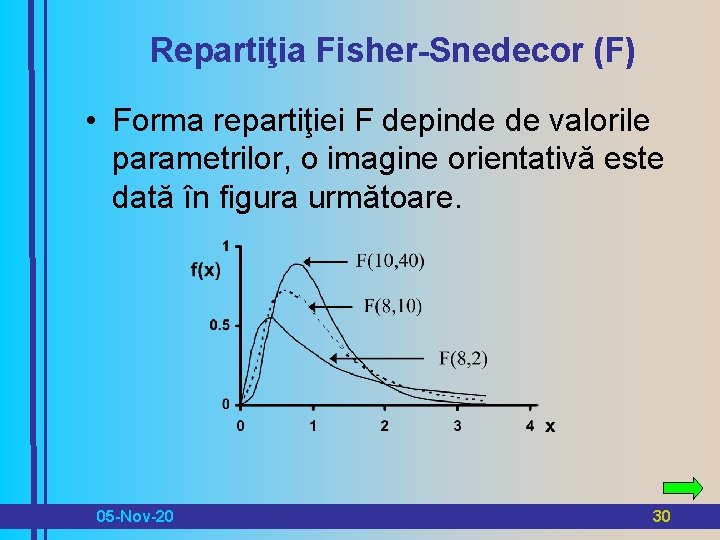
Repartiţia Fisher-Snedecor (F) • Forma repartiţiei F depinde de valorile parametrilor, o imagine orientativă este dată în figura următoare. 05 -Nov-20 30

Repartiţia Fisher-Snedecor (F) • Pentru o v. a. F, repartizată F(n 1, n 2), se obţine: dacă n 2 > 2. pentru n 2 > 4. • Quantilele repartiţiei F, notate F ; n 1; n 2, sunt tabelate pentru diferite valori uzuale lui şi diferite grade de libertate. Repartiţia F nu este simetrică, între quantile există relaţia 05 -Nov-20 31

Repartiţia binomială Repartiţiile prezentate până acum sunt repartiţii definite pentru variabile aleatoare continue. • Repartiţia binomială, denumită şi repartiţia lui Bernoulli, este definită pentru o variabilă discretă. • Modelul binomial are ca punct de plecare schema bilei revenite: – Într‑o urnă sunt bile albe şi bile negre, în total N bile. Probabilitatea de a extrage o bilă neagră este p (= numărul de bile negre raportat la numărul total de bile). După ce se extrage o bilă aceasta se repune în urnă. Se cere probabilitatea ca în urma a n extrageri să se obţină k bile negre (şi, evident, n–k bile albe). • Se numeşte încercare obţinerea unui rezultat individual şi experiment o suită de încercări. 05 -Nov-20 32

Repartiţia binomială • Pentru ca o variabilă empirică să poată fi modelată printr‑o v. a. repartizată binomial este necesar să fie îndeplinite anumite condiţii. – Variabila trebuie să fie dihotomică, adică să aibă doar două valori posibile (alb/negru, bărbat/femeie, încadrat/şomer etc. ). Cele două valori sunt notate succes, insucces. – Probabilităţile asociate valorilor succes, insucces trebuie să fie aceleaşi pentru tot experimentul. Notăm probabilitatea evenimentului de a obţine valoarea succes cu p, adică P(succes) = p. Rezultă că P(insucces) = q = 1–p (pentru că variabila este dihotomică). – Încercările trebuie să fie independente între ele (obţinerea unui rezultat anumit la o încercare nu influenţează celelalte încercări). – Încercările trebuie să fie identice prin aceea că procedura de obţinere este aceeaşi pe toată durata experimentului. Aceasta este mai mult o recomandare practică urmărind păstrarea constanţei probabilităţilor în experiment. 05 -Nov-20 33

Repartiţia binomială • • Repartiţia binomială se notează cu Bi(n; p), întrucât n şi p sunt parametrii definitorii ai funcţiei. Termenul de binomial este introdus pentru că probabilităţile P(n; r) se obţin ca termeni ai dezvoltării binomiale (p + q)n. Variabila aleatoare X, considerată în modelul binomial, este numărul de succese apărute într‑un experiment. Valorile posibile ale lui X, într‑un experiment cu n încercări, sunt 0, 1, 2, …, n. Se poate arăta că, în condiţiile date, v. a. X ia aceste valori cu probabilităţile: r = 1, 2, …, n unde p este probabilitatea unui succes, q=1 p este probabilitatea unui insucces, iar n este numărul de încercări din experiment. 05 -Nov-20 34

Repartiţia binomială • Valorile tipice ale repartiţiei binomiale sunt: • Funcţie de repartiţie este o funcţie în trepte, specifică unei distribuţii discrete. • Forma distribuţiei depinde de raportul dintre p şi q: – distribuţia este simetrică pentru p = q, asimetria se accentuează o dată cu diferenţa dintre p şi q. – În figură se poate observa simetria distribuţiei Bi(8; 0, 5), adică repartiţia caracterizată de p = q = 0, 5, precum şi asimetria pronunţată a distribuţiei Bi(5; 0, 8) în care p = 0, 8 iar q = 0, 2. 05 -Nov-20 35

Repartiţia binomială Aplicaţie la repartizarea obervaţiilor în clase • Forma repartiţiei binomiale cu p = q = 1/2 este simetrică şi, pentru un număr suficient de mare de observaţii, repartiţia binomială este aproximată de repartiţia normală. Aceste constatări pot servi în două situaţii importante în practică: – verificarea apropierii măsurătorilor efectuate de o repartiţie normală, mai ales în cazul când datele sunt grupate într‑un număr de clase; – gradarea unei scale continue atunci când dispunem de un număr suficient de mare de observaţii pentru o variabilă care se presupune continuă. • Într‑o repartiţie binomială Bi(n, 1/2) probabilităţile sunt proporţionale cu coeficienţii binomiali, deci cu numerele conţinute în triunghiul lui Pascal: o clasă: 1 2 clase: 1 1 3 clase: 1 2 1 4 clase: 1 3 3 1 5 clase: 1 4 6 4 1 … • Atunci când se doreşte împărţirea într un număr de clase a observaţiilor unei variabile pentru care se cunoaşte, sau se impune, normalitatea, efectivele claselor trebuie să fie proporţionale cu numerele din triunghiul lui Pascal aflate pe linia corespunzătoare numărului de clase. 05 -Nov-20 36