Hypothesis Tests and Confident Intervals in Multiple Regressors



















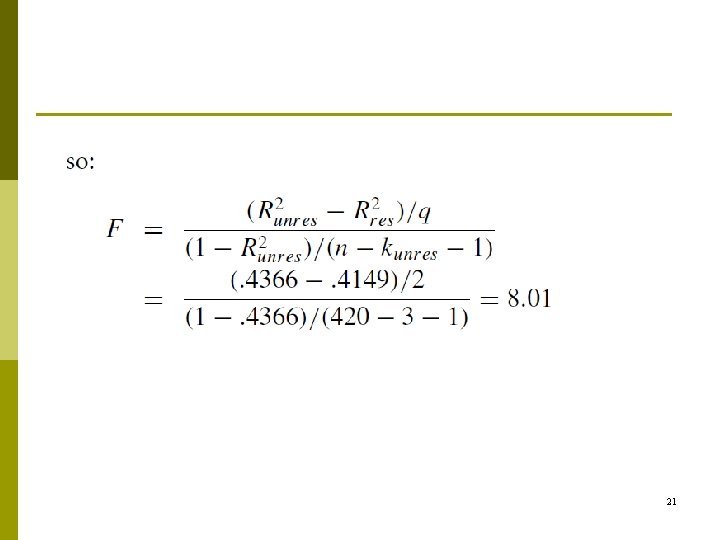
















- Slides: 39

Hypothesis Tests and Confident Intervals in Multiple Regressors 1

Outline Hypothesis Testing p Joint Hypotheses p Single Restriction Test p Test Score Data p 2

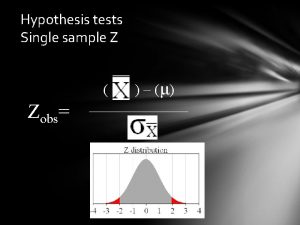
Hypothesis Tests and Confidence Intervals for a Single Coefficient p is approximately distributed N(0, 1). (CLT) p Thus hypotheses on can be tested using the usual t-statistic, and confidence intervals are constructed as So too for and are generally not independently distributed so neither are their t-statistics (more on this later). p p p 3

Example: The California class size data p p The coefficient on STR in (2) is the effect on Test Score of a unit change in STR, holding constant the percentage of English Learners in the district. Coefficient on STR falls by one-half. 95% confidence interval for coefficient on STR in (2) is {− 1. 10 ± 1. 96 0. 43} = (− 1. 95, − 0. 26) The t-statistic for STR = − 1. 10/0. 43 = − 2. 54, so we reject the 4 hypothesis at the 5 % significance level.

Tests of Joint Hypotheses Let Expn = expenditures per pupil and consider the population regression model The null hypothesis that “school resources don’t matter, ” and the alternative that they do, corresponds to 5

A joint hypothesis specifies a value for two or more coefficients, that is, it imposes a restriction on two or more coefficients. p A “common sense” test is to reject if either of the individual tstatistics exceeds 1. 96 in absolute value. p But this “common sense” approach doesn’t work. The resulting test doesn’t have the right significance level. 6

Here’s why: Calculate the probability of incorrectly rejecting the null using the “common sense” test based on the two individual tstatistics. p To simplify the calculation, suppose that and are independently distributed. Let t 1 and t 2 be the t-statistics. p The “common sense” test is reject if |t 1|>1. 96 and/or |t 2| > 1. 96. What is the probability that this “common sense” test rejects H 0 when H 0 is actually true? (It should be 5%. ) 7

Probability of incorrectly rejecting the null 8

which is not the desired 5%. 9

The size of a test is the actual rejection rate under the null hypothesis. p The size of the “common sense” test isn’t 5%. p Its size actually depends on the correlation between t 1 and t 2 (and thus on the correlation between and ). Two Solutions. p Use a different critical value in this procedure - not 1. 96 (this is the “Bonferroni method” – see App. 7. 1). This is rarely used in practice. p Use a different test statistic that test both and at once— the F-statistic. 10

The F-statistic tests all parts of a joint hypothesis at once. Formula for the special case of the joint hypothesis and in a regression with two regressors. where estimates the correlation between t 1 and t 2. Reject when F is “large. ” 11

The F-statistic testing p p and The F-statistic is large when t 1 and/or t 2 is large. The F-statistic corrects (in just the right way) for the correlation between t 1 and t 2. 12

Large-sample distribution of the F-statistic Consider a special case that t 1 and t 2 are independent, so. In large samples the formula becomes p p Under the null, t 1 and t 2 have standard normal distributions that, in this special case, are independent. The large-sample distribution of the F-statistic is the distribution of the average of two independently distributed squared standard normal random variables. 13

p p The chi-squared distribution with q degrees of freedom ( ) is defined to be the distribution of the sum of q independent squared standard normal random variables. In large samples, F -statistic is distributed as. Selected large-sample critical values of 14

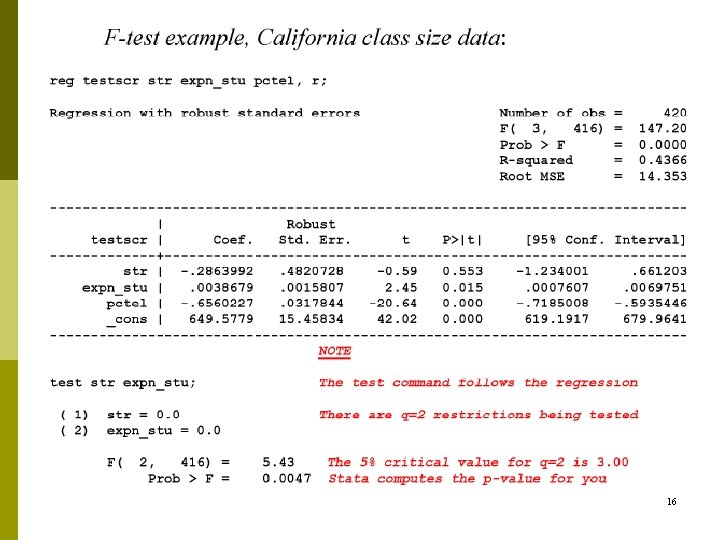
p p Compute p-value using the F-statistic: p-value = tail probability of the distribution beyond the F -statistic actually computed. Implementation in STATA Use the “test” command after the regression. Example: Test the joint hypothesis that the population coefficients on STR and expenditures per pupil (expn_stu) are both zero, against the alternative that at least one of the population coefficients is nonzero. 15

16

The homoskedasticity-only F-statistic To compute the homoskedasticity-only F-statistic p Use the previous formulas, but using homoskedasticity-only standard errors. Or p Run two regressions, one under the null hypothesis (the “restricted” regression) and one under the alternative hypothesis (the “unrestricted” regression). p The second method gives a simple formula. 17

The “restricted” and “unrestricted” regressions Example: are the coefficients on STR and Expn zero? Restricted population regression (that is, under H 0): Unrestricted population regression (under H 1): p p The number of restrictions under H 0 = q = 2. The fit will be better (R 2 will be higher) in the unrestricted regression (why? ) 18

By how much must the R 2 increase for the coefficients on Expn and Pct EL to be judged statistically significant? Simple formula for the homoskedasticity-only F-statistic where = the R 2 for the restricted regression = the R 2 for the unrestricted regression q = the number of restrictions under the null = the number of regressors in the unrestricted regression. 19

Example: Restricted regression: Unrestricted regression: 20
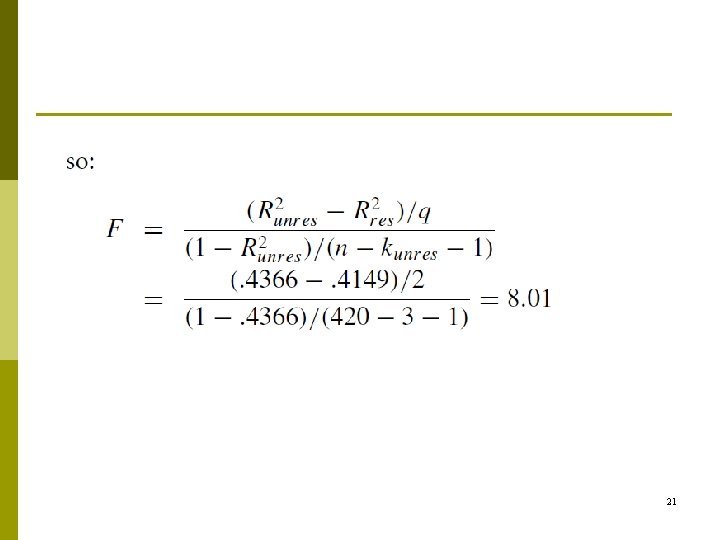
21

The homoskedasticity-only F-statisticsummary p p p The homoskedasticity-only F-statistic rejects when adding the two variables increased the R 2 by “enough” - that is, when adding the two variables improves the fit of the regression by “enough. ” If the errors are homoskedastic, then the homoskedasticityonly F-statistic has a large-sample distribution that is. But if the errors are heteroskedastic, the large-sample distribution is a mess and is not. 22

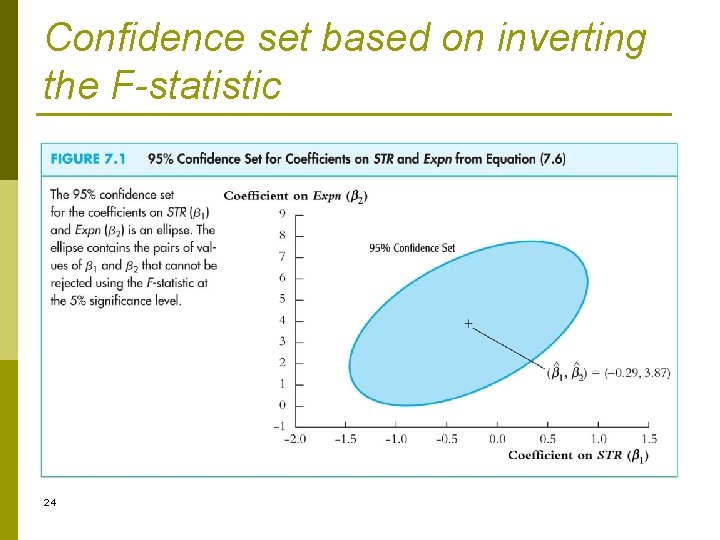
Joint confidence sets ctd. 23

Confidence set based on inverting the F-statistic 24

Summary: testing joint hypotheses p p The “common-sense” approach of rejecting if either of the tstatistics exceeds 1. 96 rejects more than 5% of the time under the null (the size exceeds the desired significance level). The heteroskedasticity-robust F-statistic is built in to STATA (“test” command). This tests all q restrictions at once. For large n, F is distributed as. The homoskedasticity-only F-statistic is important historically (and thus in practice), and is intuitively appealing, but invalid when there is heteroskedasticity. 25

Testing Single Restrictions on Multiple Coefficients Consider the null and alternative hypothesis, This null imposes a single restriction (q = 1) on multiple coefficients - it is not a joint hypothesis with multiple restrictions (compare with = 0 and = 0). 26

Two methods for testing single restrictions on multiple coefficients: p Rearrange (“transform”) the regression. Rearrange the regressors so that the restriction becomes a restriction on a single coefficient in an equivalent regression. p Perform the test directly. Some software, including STATA, lets you test restrictions using multiple coefficients directly. 27

Method 1: Rearrange (”transform”) the regression. Add and subtract where 28

(a) Original system: (b) Rearranged (”transformed”) system: so The testing problem is now a simple one: test whether γ 1 = 0 in specification (b). 29

Method 2: Perform the test directly Example: To test, using STATA, whether pctel, r test str=expn = : regress testscore str expn 30

Analysis of the Test Score Data A general approach to variable selection and “model specification” p Specify a “base” or “benchmark” model. p Specify a range of plausible alternative models, which include additional candidate variables. p Does a candidate variable change the coefficient of interest ( )? 31

p p p Is a candidate variable statistically significant? Use judgment, not a mechanical recipe. And don’t just maximize R 2. 32

Digression about measures of fit… 33

Variables we would like to see in the California data set School characteristics p student-teacher ratio p teacher quality p computers (non-teaching resources) per student p measures of curriculum design Student characteristics p English proficiency p availability of extracurricular enrichment p home learning environment p parent’s education level 34

Variables actually in the California class size data set p p p student-teacher ratio (STR) percent English learners in the district (Pct. EL) percent eligible for subsidized/free lunch percent on public income assistance average district income 35

A look at more of the California data 36

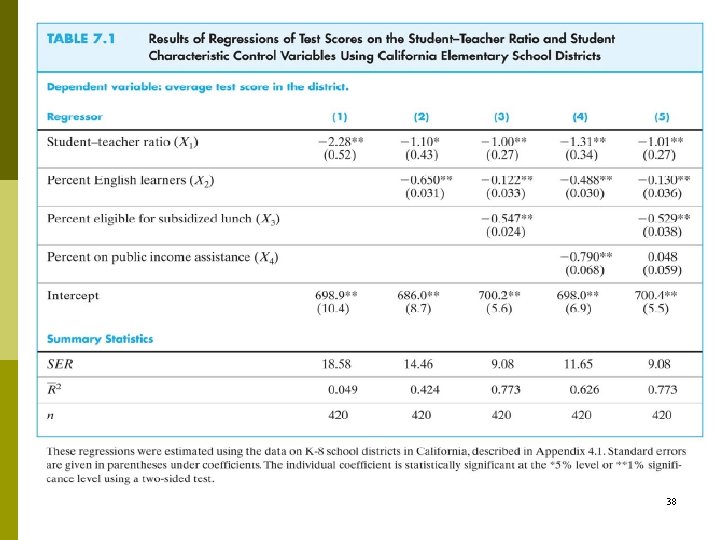
Digression: presentation of regression results in a table p p p Listing regressions in “equation” form can be cumbersome with many regressors and many regressions. Tables of regression results can present the key information compactly. Information to include: n variables in the regression (dependent and independent). n estimated coefficients. n standard errors. n results of F-tests of joint hypotheses. n some measure of fit (adjusted R 2). n number of observations. 37

38

Summary: Multiple Regression p p Multiple regression allows you to estimate the effect on Y of a change in X 1, holding X 2 constant. If you can measure a variable, you can avoid omitted variable bias from that variable by including it. There is no simple recipe for deciding which variables belong in a regression - you must exercise judgment. One approach is to specify a base model - relying on a-priori reasoning - then explore the sensitivity of the key estimate(s) in alternative specifications. 39
 Chapter 20 more about tests and intervals
Chapter 20 more about tests and intervals Regressors meaning
Regressors meaning Stochastic regressors
Stochastic regressors Stochastic regressors
Stochastic regressors Ace different tests iq tests but
Ace different tests iq tests but Hypothesis examples in research
Hypothesis examples in research Null hypothesis
Null hypothesis Nebular hypothesis and protoplanet hypothesis venn diagram
Nebular hypothesis and protoplanet hypothesis venn diagram Assertive confidence
Assertive confidence Fm 6-22 army leadership
Fm 6-22 army leadership Jaydon doesn't realize that his alcohol abuse and neglect
Jaydon doesn't realize that his alcohol abuse and neglect Developing null and alternative hypothesis
Developing null and alternative hypothesis Confident personality traits
Confident personality traits Confident
Confident Adventure word formation
Adventure word formation Healthy confident individuals
Healthy confident individuals Means
Means Confident similes
Confident similes Confident
Confident 95 size means
95 size means Words that have the same denotation are called
Words that have the same denotation are called B confident
B confident Multiple regression analysis inference
Multiple regression analysis inference Hypothesis for multiple regression
Hypothesis for multiple regression Multiple factor hypothesis
Multiple factor hypothesis Dialogue evaluation via multiple hypothesis ranking
Dialogue evaluation via multiple hypothesis ranking Delayed multiple baseline design
Delayed multiple baseline design Shared memory mimd architecture
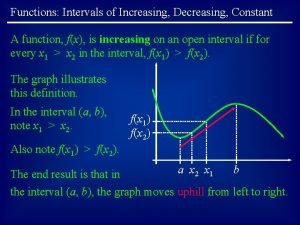
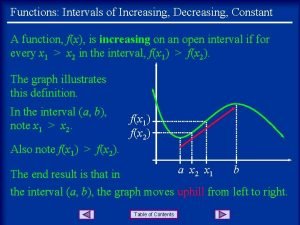
Shared memory mimd architecture How to find increasing and decreasing intervals on a graph
How to find increasing and decreasing intervals on a graph Increasing function
Increasing function Removable and nonremovable discontinuity
Removable and nonremovable discontinuity How to draw histogram with different class width
How to draw histogram with different class width Increasing intervals
Increasing intervals Error interval
Error interval End behavior of a quadratic function
End behavior of a quadratic function Importance of confidence interval
Importance of confidence interval Mild left axis deviation
Mild left axis deviation How to do error intervals
How to do error intervals Error interval questions
Error interval questions What is the highest mark you can get on a foundation paper
What is the highest mark you can get on a foundation paper