Nonparametric tests and ANOVAs What you need to

Nonparametric tests and ANOVAs: What you need to know

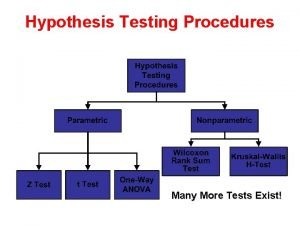
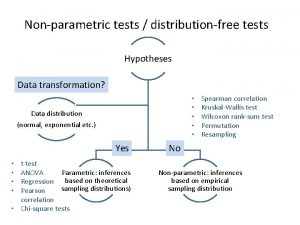
Nonparametric tests • Nonparametric tests are usually based on ranks • There are nonparametric versions of most parametric tests

Parametric One-sample and Paired t-test Two-sample t-test Nonparametric Sign test Mann-Whitney U-test

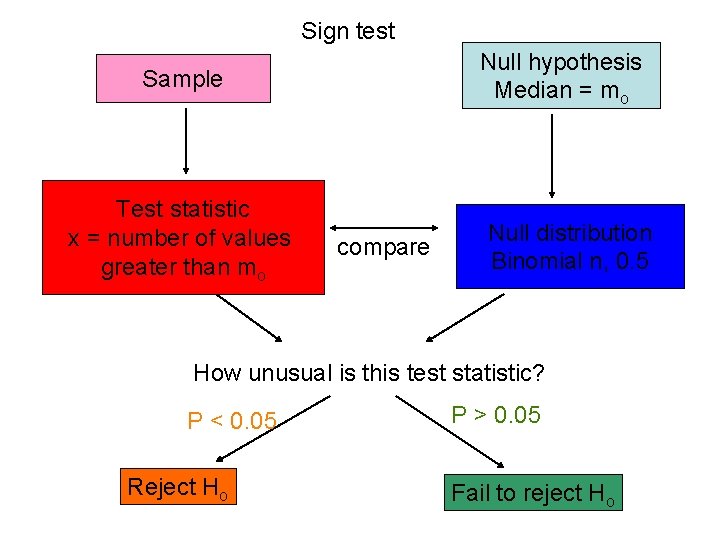
Quick Reference Summary: Sign Test • What is it for? A non-parametric test to compare the medians of a group to some constant • What does it assume? Random samples • Formula: Identical to a binomial test with po= 0. 5. Uses the number of subjects with values greater than and less than a hypothesized median as the test statistic. P(x) = probability of a total of x successes p = probability of success in each trial n = total number of trials P = 2 * Pr[x X]

Sign test Null hypothesis Median = mo Sample Test statistic x = number of values greater than mo compare Null distribution Binomial n, 0. 5 How unusual is this test statistic? P < 0. 05 Reject Ho P > 0. 05 Fail to reject Ho

Quick Reference Summary: Mann-Whitney U Test • What is it for? A non-parametric test to compare the central tendencies of two groups • What does it assume? Random samples • Test statistic: U • Distribution under Ho: U distribution, with sample sizes n 1 and n 2 • Formulae: n = sample size of group 1 1 n 2= sample size of group 2 R 1= sum of ranks of group 1 Use the larger of U 1 or U 2 for a two-tailed test

Mann-Whitney U test Null hypothesis The two groups Have the same median Sample Test statistic U 1 or U 2 (use the largest) compare Null distribution U with n 1, n 2 How unusual is this test statistic? P < 0. 05 Reject Ho P > 0. 05 Fail to reject Ho

Mann-Whitney U test • Large-sample approximation: Use this when n 1& n 2 are both > 10 Compare to the standard normal distribution

Mann-Whitney U Test • If you have ties: – Rank them anyway, pretending they were slightly different – Find the average of the ranks for the identical values, and give them all that rank – Carry on as if all the whole-number ranks have been used up

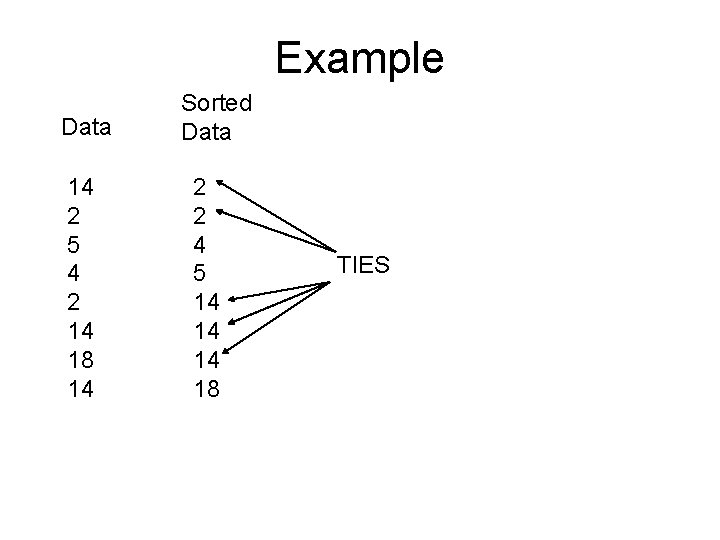
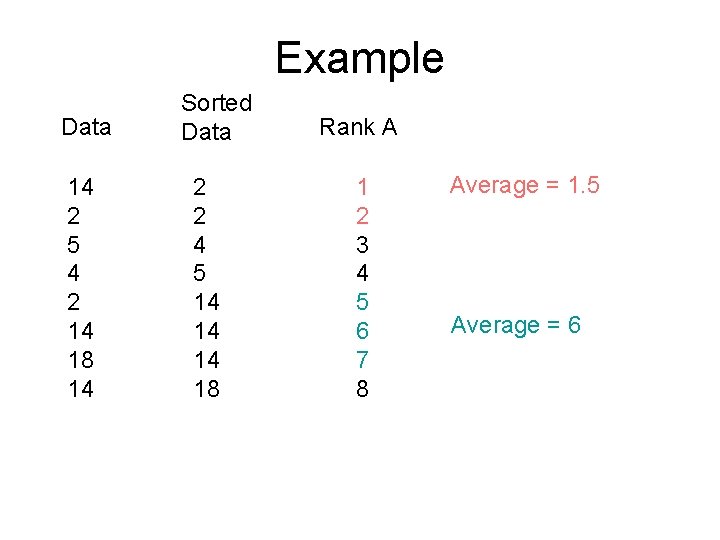
Example Data 14 2 5 4 2 14 18 14

Example Data 14 2 5 4 2 14 18 14 Sorted Data 2 2 4 5 14 14 14 18

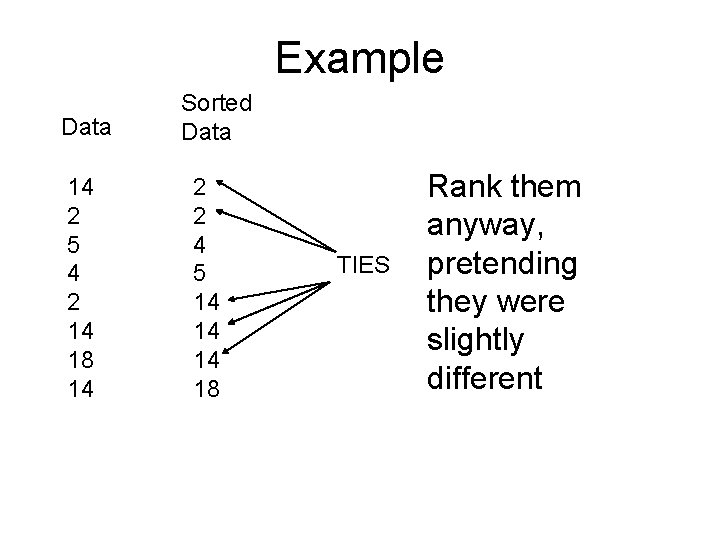
Example Data 14 2 5 4 2 14 18 14 Sorted Data 2 2 4 5 14 14 14 18 TIES

Example Data 14 2 5 4 2 14 18 14 Sorted Data 2 2 4 5 14 14 14 18 TIES Rank them anyway, pretending they were slightly different

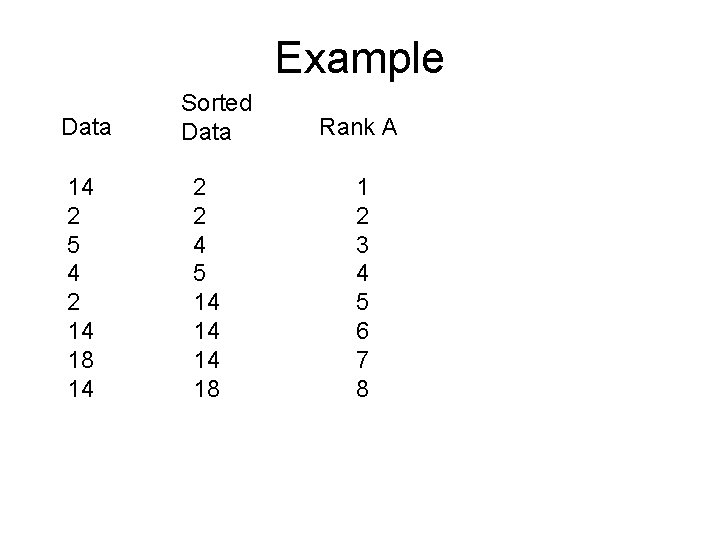
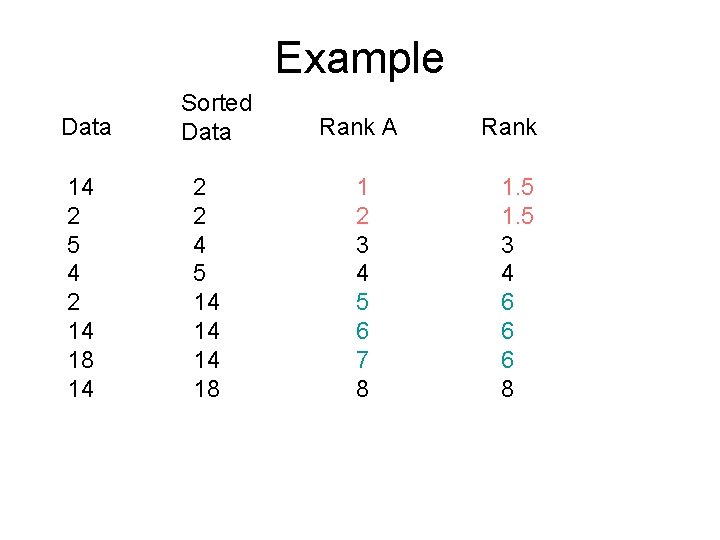
Example Data 14 2 5 4 2 14 18 14 Sorted Data 2 2 4 5 14 14 14 18 Rank A 1 2 3 4 5 6 7 8

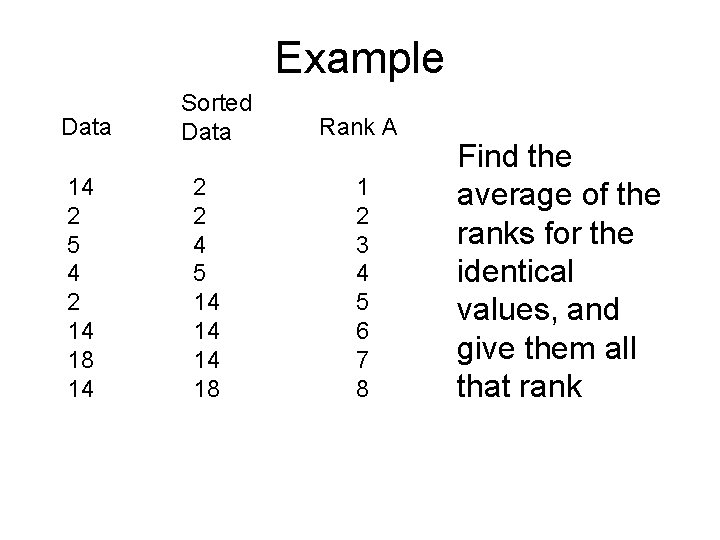
Example Data 14 2 5 4 2 14 18 14 Sorted Data 2 2 4 5 14 14 14 18 Rank A 1 2 3 4 5 6 7 8 Find the average of the ranks for the identical values, and give them all that rank

Example Data 14 2 5 4 2 14 18 14 Sorted Data 2 2 4 5 14 14 14 18 Rank A 1 2 3 4 5 6 7 8 Average = 1. 5 Average = 6

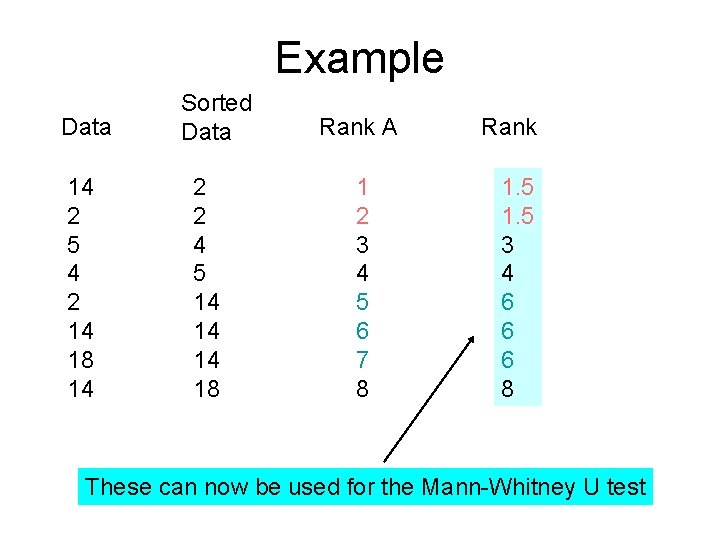
Example Data 14 2 5 4 2 14 18 14 Sorted Data 2 2 4 5 14 14 14 18 Rank A 1 2 3 4 5 6 7 8 Rank 1. 5 3 4 6 6 6 8

Example Data 14 2 5 4 2 14 18 14 Sorted Data 2 2 4 5 14 14 14 18 Rank A 1 2 3 4 5 6 7 8 Rank 1. 5 3 4 6 6 6 8 These can now be used for the Mann-Whitney U test

Benefits and Costs of Nonparametric Tests • Main benefit: – Make fewer assumptions about your data – E. g. only assume random sample • Main cost: – Reduce statistical power – Increased chance of Type II error

When Should I Use Nonparametric Tests? • When you have reason to suspect the assumptions of your test are violated – Non-normal distribution – No transformation makes the distribution normal – Different variances for two groups

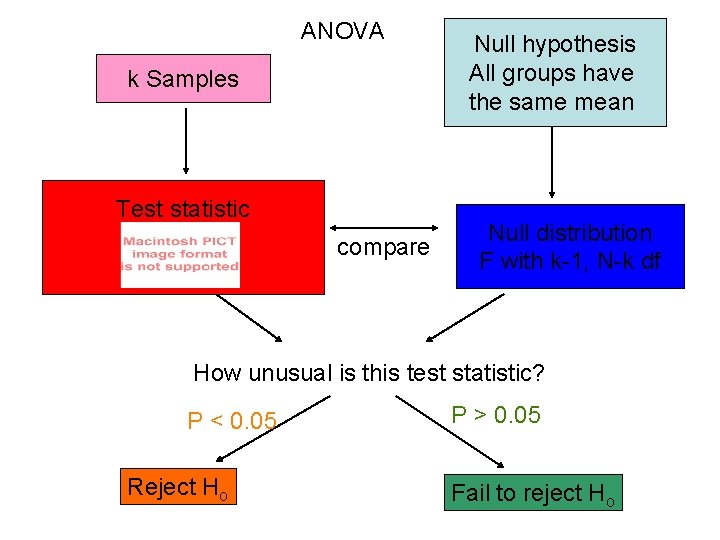
Quick Reference Summary: ANOVA (analysis of variance) • What is it for? Testing the difference among k means simultaneously • What does it assume? The variable is normally distributed with equal standard deviations (and variances) in all k populations; each sample is a random sample • Test statistic: F • Distribution under Ho: F distribution with k-1 and N-k degrees of freedom

Quick Reference Summary: ANOVA (analysis of variance) • Formulae: = mean of group i = overall mean ni = size of sample i N = total sample size

ANOVA k Samples Test statistic compare Null hypothesis All groups have the same mean Null distribution F with k-1, N-k df How unusual is this test statistic? P < 0. 05 Reject Ho P > 0. 05 Fail to reject Ho

Quick Reference Summary: ANOVA (analysis of variance) • Formulae: There a LOT of equations here, and this is the simplest possible ANOVA = mean of group i = overall mean ni = size of sample i N = total sample size

dfgroup = k-1 dferror = N-k

Sum of Squares df dfgroup = k-1 dferror = N-k Mean Squares F-ratio

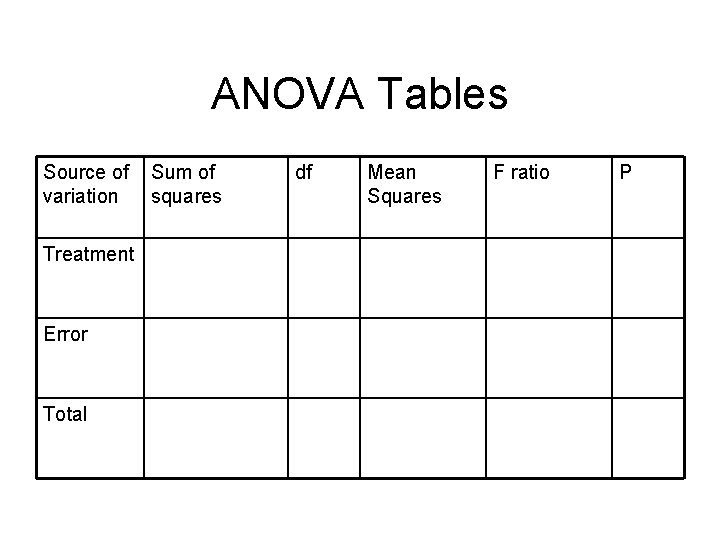
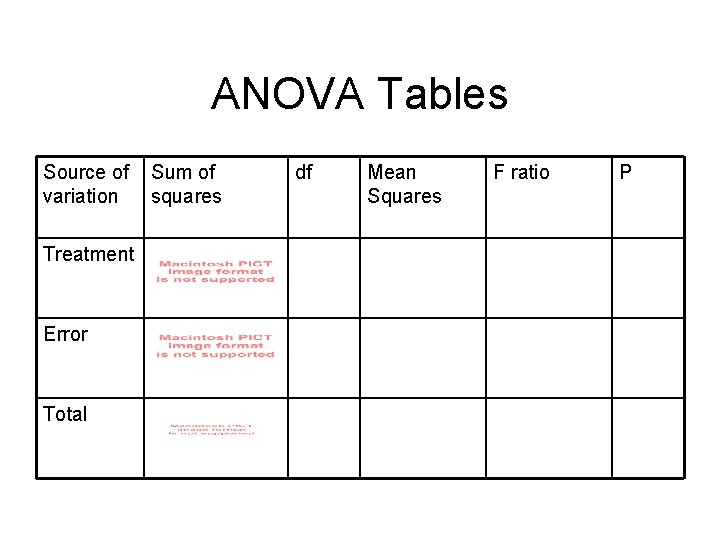
ANOVA Tables Source of variation Treatment Error Total Sum of squares df Mean Squares F ratio P

ANOVA Tables Source of variation Treatment Error Total Sum of squares df Mean Squares F ratio P

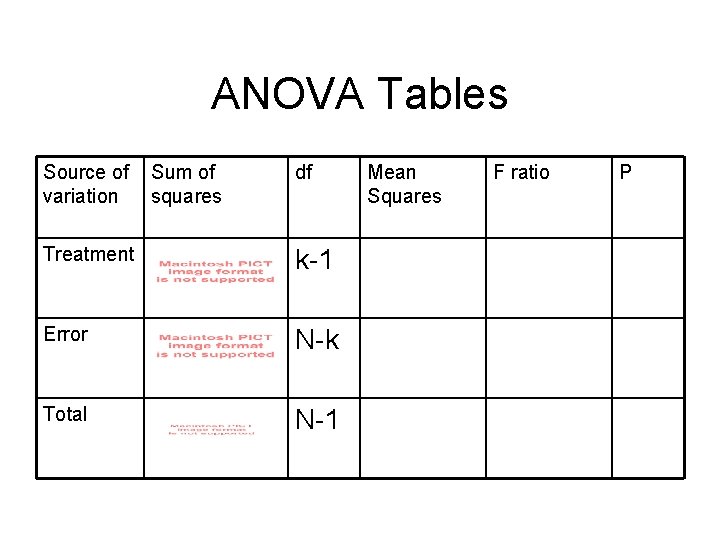
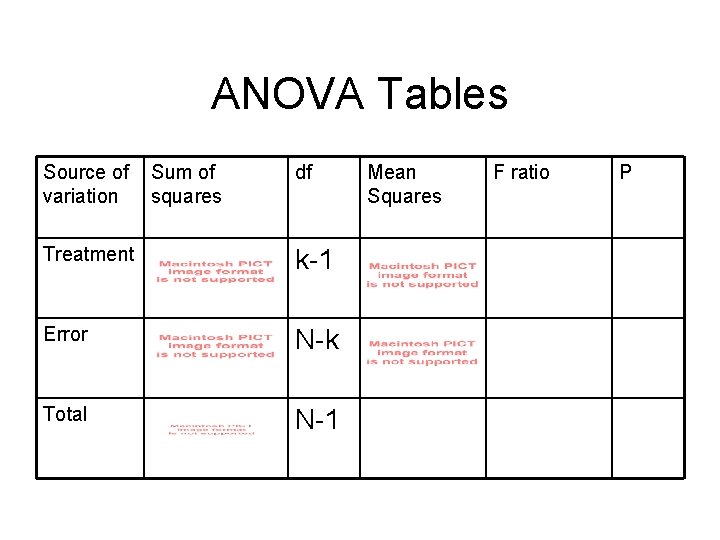
ANOVA Tables Source of variation Sum of squares df Treatment k-1 Error N-k Total N-1 Mean Squares F ratio P

ANOVA Tables Source of variation Sum of squares df Treatment k-1 Error N-k Total N-1 Mean Squares F ratio P

ANOVA Tables Source of variation Sum of squares df Treatment k-1 Error N-k Total N-1 Mean Squares F ratio P

ANOVA Tables Source of variation Sum of squares df Treatment k-1 Error N-k Total N-1 Mean Squares F ratio P *

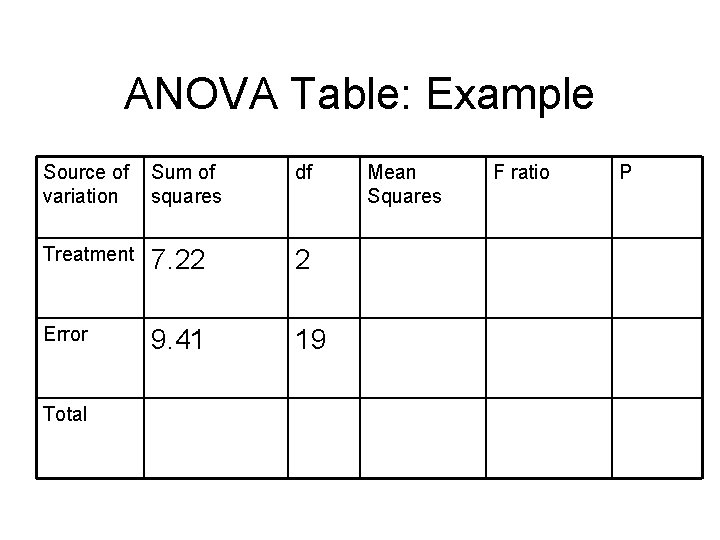
ANOVA Table: Example Source of variation Sum of squares df Treatment 7. 22 2 Error 9. 41 19 Total Mean Squares F ratio P

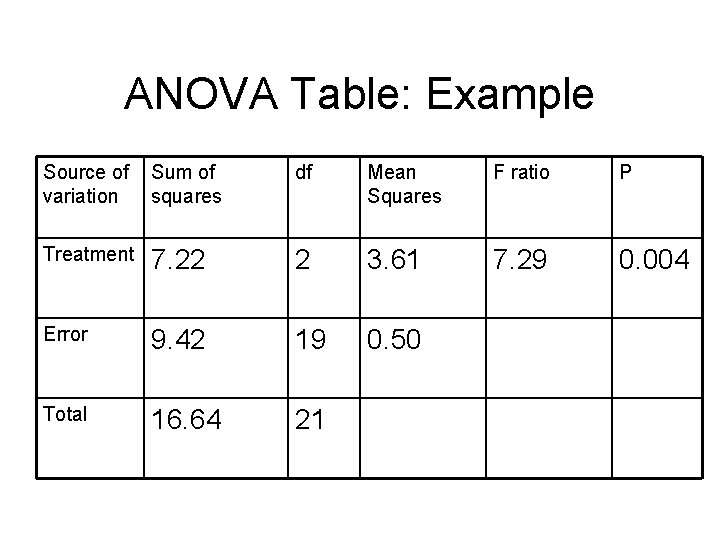
ANOVA Table: Example Source of variation Sum of squares df Mean Squares F ratio P Treatment 7. 22 2 3. 61 7. 29 0. 004 Error 9. 42 19 0. 50 Total 16. 64 21

Additions to ANOVA • R 2 value: how much variance is explained? • Comparisons of groups: planned and unplanned • Fixed vs. random effects • Repeatability

Two-Factor ANOVA • Often we manipulate more than one thing at a time • Multiple categorical explanitory variables • Example: sex and nationality

Two-factor ANOVA • Don’t worry about the equations for this • Use an ANOVA table

Two-factor ANOVA • 1. 2. 3. Testing three things: Means don’t differ among treatment 1 Means don’t differ among treatment 2 There is no interaction between the two treatments

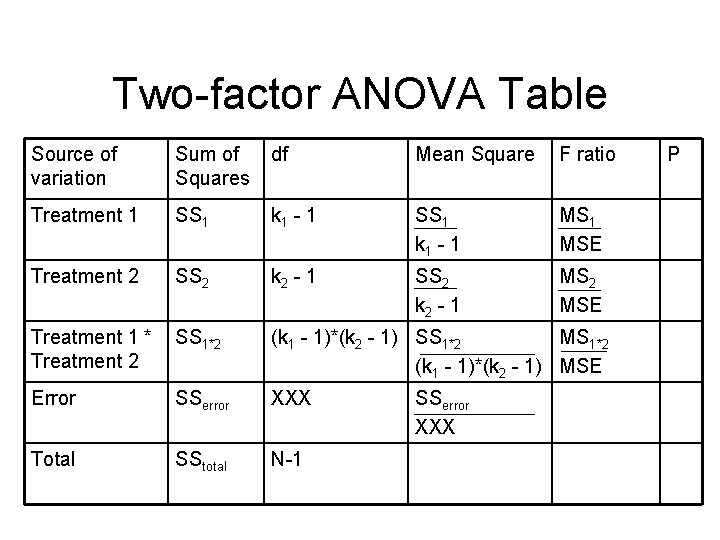
Two-factor ANOVA Table Source of variation Sum of Squares df Mean Square F ratio Treatment 1 SS 1 k 1 - 1 MSE Treatment 2 SS 2 k 2 - 1 MS 2 MSE Treatment 1 * Treatment 2 SS 1*2 (k 1 - 1)*(k 2 - 1) SS 1*2 MS 1*2 (k 1 - 1)*(k 2 - 1) MSE Error SSerror XXX Total SStotal N-1 SSerror XXX P