Standard Trend Models Trend Curves Purposes of a

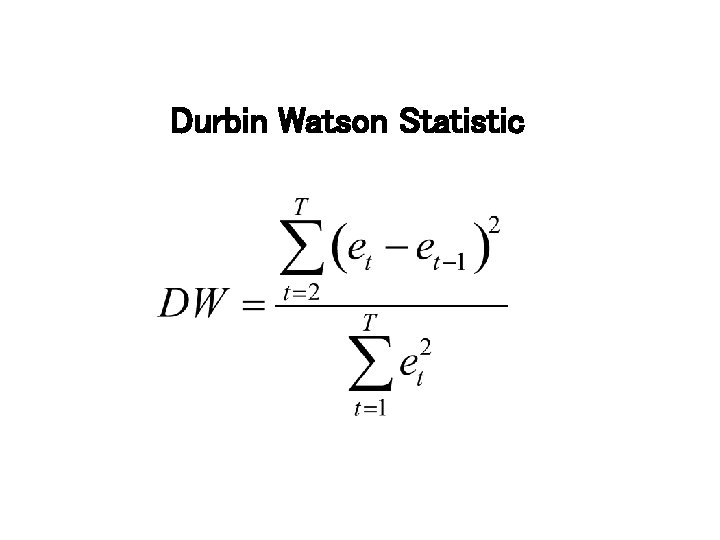
  • Slides: 19
Download presentation
Standard Trend Models

Standard Trend Models

Trend Curves • Purposes of a Trend Curve: 1. Forecasting the long run 2.

Trend Curves • Purposes of a Trend Curve: 1. Forecasting the long run 2. Estimating the growth rate

Standard Trend Curves • Key Properties: – have a simple form – have good

Standard Trend Curves • Key Properties: – have a simple form – have good track records – software for fitting is widely available

Types of Standard Trend Curves • For unbounded data: – linear – quadratic –

Types of Standard Trend Curves • For unbounded data: – linear – quadratic – exponential • For bounded (S shaped) data: – logistic – Gompertz

Unbounded Trend • Linear: Yt = b 0 + b 1 t + e

Unbounded Trend • Linear: Yt = b 0 + b 1 t + e • Quadratic: Yt = b 0 + b 1 t + b 2 t 2 + e • Log-linear: ln(Yt)= b 0 + b 1 t + e

Two Standard S Curves 1. Logistic Curve 2. Gompertz Curve

Two Standard S Curves 1. Logistic Curve 2. Gompertz Curve

S – Curves (Life Cycle Theory) 4 Stages of New Technology Life Cycle 1.

S – Curves (Life Cycle Theory) 4 Stages of New Technology Life Cycle 1. Slow growth at the beginning stage 2. Rapid growth 3. Slow growth during the mature stage 4. Decline during the final stage

S - Curves Point of Inflection Y second derivative = 0 Y(ln(a) /b) =

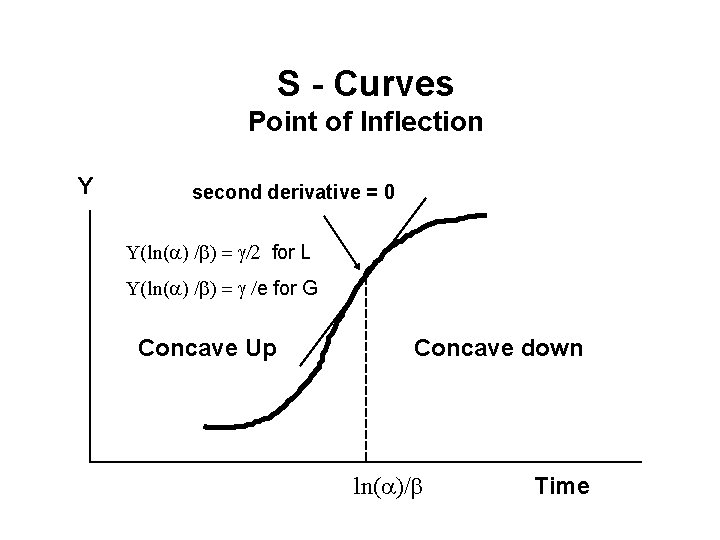
S - Curves Point of Inflection Y second derivative = 0 Y(ln(a) /b) = g/2 for L Y(ln(a) /b) = g /e for G Concave Up Concave down ln(a)/b Time

Model Selection Process 1. Timeplot Linear / Quadratic Exponential (linear in log) 2. Take

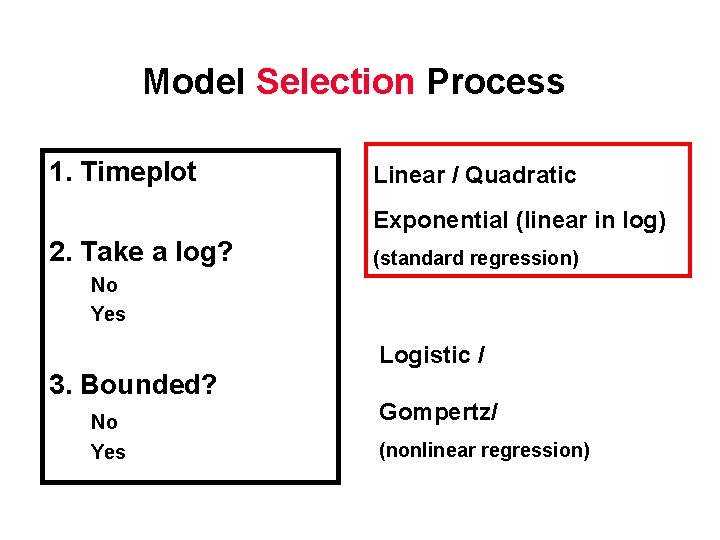
Model Selection Process 1. Timeplot Linear / Quadratic Exponential (linear in log) 2. Take a log? (standard regression) No Yes Logistic / 3. Bounded? No Yes Gompertz/ (nonlinear regression)

Nonlinear Least Squares • SPSS is one of the few statistics packages that provide

Nonlinear Least Squares • SPSS is one of the few statistics packages that provide routines for fitting nonlinear regression models. • You have to provide initial estimates for parameters.

Getting Initial Parameter Values - Logistic Curve Estimate g from data, and compute Regress

Getting Initial Parameter Values - Logistic Curve Estimate g from data, and compute Regress the variable on t.

Getting Initial Parameter Values - Gompertz Curve Estimate g from data, and compute Regress

Getting Initial Parameter Values - Gompertz Curve Estimate g from data, and compute Regress the variable on t.

Durbin-Watson Test

Durbin-Watson Test

White Noise Residuals • WN (white noise) – uncorrelated Ex. et ~ WN(0, s)

White Noise Residuals • WN (white noise) – uncorrelated Ex. et ~ WN(0, s) (weak WN) • iid – independent and identically distributed Ex. et ~ iid N(0, s) (strong WN)

Spurious Trend Downward Bias: Positive Auto. Correlated Residual SE of Coefficient SER

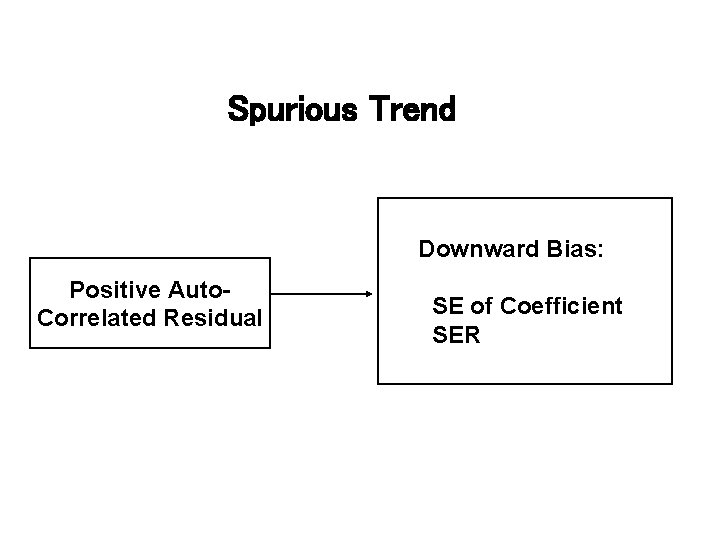
Spurious Trend Downward Bias: Positive Auto. Correlated Residual SE of Coefficient SER

Trend Model With Correlated Residual

Trend Model With Correlated Residual

Durbin Watson Statistic

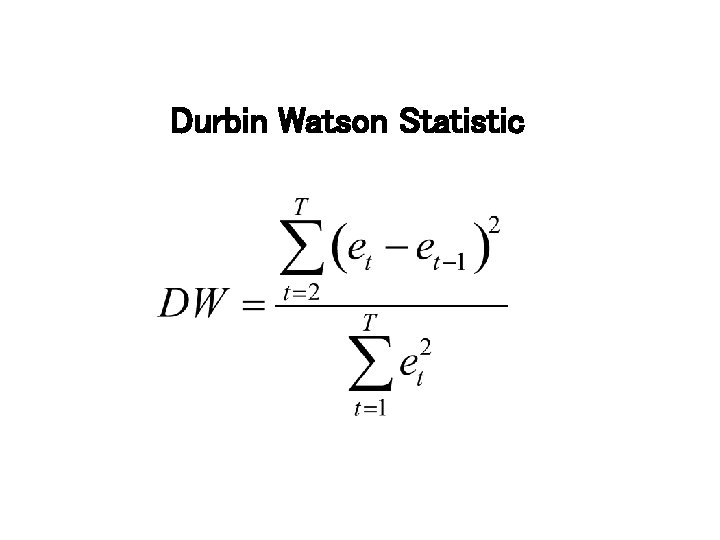
Durbin Watson Statistic

Some Key Values of DW Stat • E(DW) = 2 if H 0 •

Some Key Values of DW Stat • E(DW) = 2 if H 0 • Table available for DW if H 0

DW Test • The Null and Alternative Hypotheses – H 0 : r =

DW Test • The Null and Alternative Hypotheses – H 0 : r = 0 – H 1 : r > 0 -> positive autocorrelated residual

Week 4 Curves Topics parametric curves Bezier curvesWeek 4 Curves Topics parametric curves Bezier curves
Solubility Curves Solubility curves Solubility curves can beSolubility Curves Solubility curves Solubility curves can be
SurveyingII SURVEYINGII SurveyingII CURVES SurveyingII CURVES Curves areSurveyingII SURVEYINGII SurveyingII CURVES SurveyingII CURVES Curves are
Railway Curves Transition Curves Transition Curves An easementRailway Curves Transition Curves Transition Curves An easement
UNIT5 Curves and Surfaces Curves Curves are oneUNIT5 Curves and Surfaces Curves Curves are one
UNIT 4 CURVES CURVES Curves generally used toUNIT 4 CURVES CURVES Curves generally used to
METODE ANALISIS TREND Trend Non Linier TREND KUADRATIKMETODE ANALISIS TREND Trend Non Linier TREND KUADRATIK
TREND ANALZ Dr Hakan ADANACIOLU TREND KAVRAMI TrendTREND ANALZ Dr Hakan ADANACIOLU TREND KAVRAMI Trend
PORTFOLIO Standard 1 Standard 2 Standard 3 StandardPORTFOLIO Standard 1 Standard 2 Standard 3 Standard
PORTFOLIO Standard 1 Standard 2 Standard 3 StandardPORTFOLIO Standard 1 Standard 2 Standard 3 Standard
Standard I Standard VIIIE Standard III Standard VStandard I Standard VIIIE Standard III Standard V
Trend Reader Standard 2 This generation of TrendTrend Reader Standard 2 This generation of Trend
RegressionBased Trend Models Example 14 1 Regressionbased trendRegressionBased Trend Models Example 14 1 Regressionbased trend
MODELS AND TECHNOLOGICAL DESIGN MODELS MODELS Models helpMODELS AND TECHNOLOGICAL DESIGN MODELS MODELS Models help
Last Time Parametric Curves Splines Hermite curves BezierLast Time Parametric Curves Splines Hermite curves Bezier
Density Curves and Normal Distributions Density Curves SoDensity Curves and Normal Distributions Density Curves So
Smooth Curves Dr Scott Schaefer 1 Smooth CurvesSmooth Curves Dr Scott Schaefer 1 Smooth Curves
Horizontal Curves n Circular Curves n n nHorizontal Curves n Circular Curves n n n