RegressionBased Trend Models Example 14 1 Regressionbased trend

Regression-Based Trend Models Example 14. 1

Regression-based trend models • A special case of simple regression is when the only explanatory variable is time, usually labeled t (rather than X). • In this case, the dependent variable Y is a time series variable, such as a company’s monthly sales, and the purpose of the regression is to see whether this dependent variable follows a trend through time. – With a linear trend line, the variable changes by a constant amount each period. – With an exponential trend line, the variable changes by a constant percentage each period. • The following example demonstrates how easily trends can be estimated with Excel. Winston/Albright Practical Management Science, 4 e South-Western/Cengage Learning © 2012 Thomson/South-Western 2007 ©

Example 14. 1: Exponential Growth. xlsx • The Best Chips Company produces and sells potato chips throughout the country. • Its sales have been growing steadily over the past 10 years, as shown on the next slide and in this file. • The company wants to predict its sales for the next couple of years, assuming that the upward trend it has observed in the past 10 years will continue in the future. • How should the company proceed? Winston/Albright Practical Management Science, 4 e South-Western/Cengage Learning © 2012 Thomson/South-Western 2007 ©
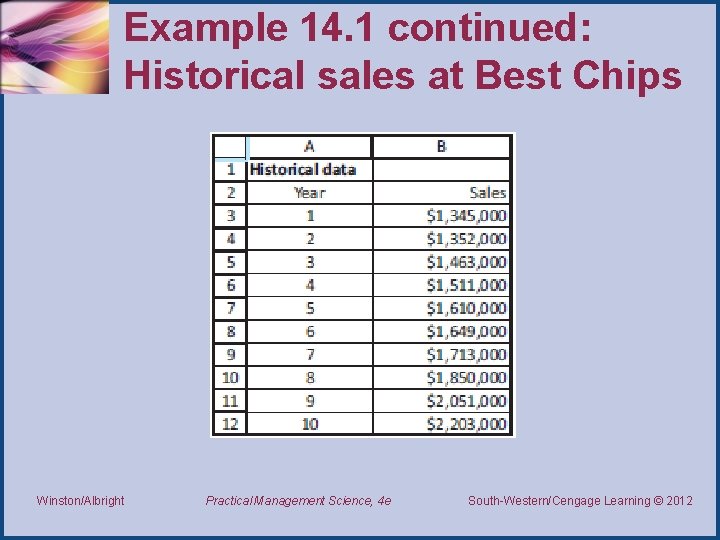
Example 14. 1 continued: Historical sales at Best Chips Winston/Albright Practical Management Science, 4 e South-Western/Cengage Learning © 2012 Thomson/South-Western 2007 ©

Example 14. 1 continued: Solution • We begin by creating the scatterplot of Sales versus Year shown on the next slide. • Sales are clearly increasing through time, but it is not absolutely clear whether they are increasing at a constant rate, which would favor a linear trendline, or at an increasing rate, which would favor an exponential trendline. • Therefore, we try fitting both of these. Winston/Albright Practical Management Science, 4 e South-Western/Cengage Learning © 2012 Thomson/South-Western 2007 ©
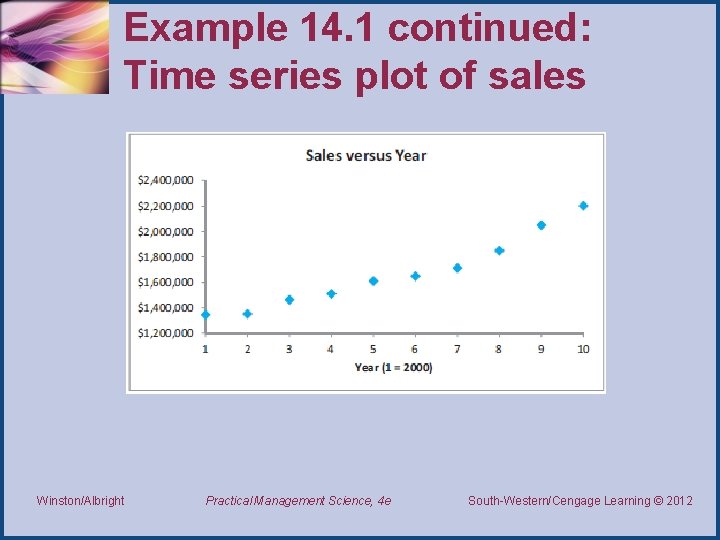
Example 14. 1 continued: Time series plot of sales Winston/Albright Practical Management Science, 4 e South-Western/Cengage Learning © 2012 Thomson/South-Western 2007 ©

Example 14. 1 continued: Solution • To superimpose a linear trendline on any scatterplot, right-click on any point on the chart and then select the Add Trendline menu item. • This brings up the dialog box shown here. Winston/Albright Practical Management Science, 4 e South-Western/Cengage Learning © 2012 Thomson/South-Western 2007 ©

Example 14. 1 continued: Solution • You can select any of six types of trendlines. • For now, select the default Linear option. Also, click on the Options tab and check the Display equation box. • The result is shown on the next slide. • This figure shows the best-fitting straight line to the points, and it indicates that the equation of this straight line is y = 92, 091 x +1, 168, 200. Winston/Albright Practical Management Science, 4 e South-Western/Cengage Learning © 2012 Thomson/South-Western 2007 ©
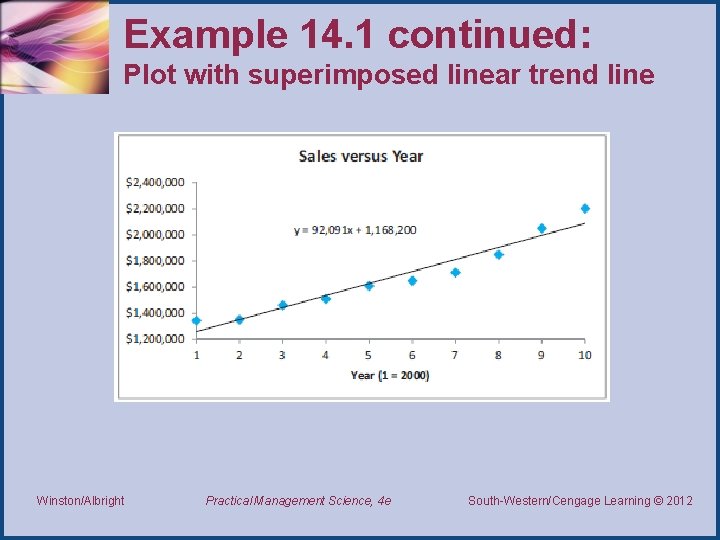
Example 14. 1 continued: Plot with superimposed linear trend line Winston/Albright Practical Management Science, 4 e South-Western/Cengage Learning © 2012 Thomson/South-Western 2007 ©

Example 14. 1 continued: Solution • Here, y corresponds to sales and x corresponds to year. • The most important part of this equation is the coefficient of x, 92, 091. It implies that sales are increasing by $92, 091 per year—if we believe that the linear trendline provides a good fit. • To obtain an exponential trendline, we go through the same procedure except that we select the Exponential option in the dialog box. Winston/Albright Practical Management Science, 4 e South-Western/Cengage Learning © 2012 Thomson/South-Western 2007 ©

Example 14. 1 continued: Solution • The resulting curve is shown below. • The equation for the curve is y 1. 2278 e 0. 0541 x. • The most important part of this equation is the coefficient in the exponent, 0. 0541. • It implies that sales are increasing by approximately 5. 4% per year. Winston/Albright Practical Management Science, 4 e South-Western/Cengage Learning © 2012 Thomson/South-Western 2007 ©

Example 14. 1 continued: Solution • Which of these trendlines provides the better fit? • We can proceed in two ways. – First, we can “eyeball” it. Looking at the superimposed trendlines, it appears that the exponential fit is slightly better. – The typical way to measure fits to a trendline through time is to calculate the historical predictions from each curve and the corresponding absolute percentage errors (APEs). • We find the predictions by plugging the year indexes (1 to 10) into the trendline equations. Winston/Albright Practical Management Science, 4 e South-Western/Cengage Learning © 2012 Thomson/South-Western 2007 ©

Example 14. 1 continued: Solution • We then calculate the APE for each year from the following equation. • A measure of goodness-of-fit is then the average of these APE values, denoted by MAPE (mean absolute percentage error). • This measure is quite intuitive. Winston/Albright Practical Management Science, 4 e South-Western/Cengage Learning © 2012 Thomson/South-Western 2007 ©

Example 14. 1 continued: Solution • • All of this is implemented and shown on the next slide. To create the predictions, APEs, and MAPEs, proceed as follows: 1. Predictions. Calculate the predictions from the linear trendline by entering the formula =1168200+92091*A 53 in cell D 3 and copying it down to cell D 14. Similarly, calculate the predictions from the exponential trendline by entering the formula =1227762*EXP(0. 0541*A 3) in cell E 3 and copying it down to cell E 14. Winston/Albright Practical Management Science, 4 e South-Western/Cengage Learning © 2012 Thomson/South-Western 2007 ©
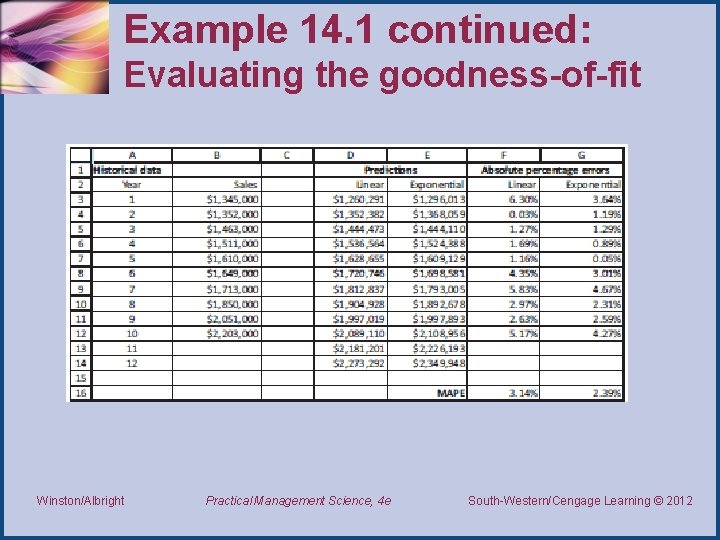
Example 14. 1 continued: Evaluating the goodness-of-fit Winston/Albright Practical Management Science, 4 e South-Western/Cengage Learning © 2012 Thomson/South-Western 2007 ©

Example 14. 1 continued: Solution 2. APE values. Calculate all of the APE values at once by entering the formula =ABS($B 3 -D 53/$B 3 in cell F 3 and copying it to the range F 3: G 12. 3. MAPE values. Calculate the MAPE for each trendline by entering the formula =AVERAGE(F 3: F 12) in cell F 16 and copying it to cell G 16. • The MAPE values confirm that the exponential trendline is slightly better than the linear trendline. Winston/Albright Practical Management Science, 4 e South-Western/Cengage Learning © 2012 Thomson/South-Western 2007 ©
- Slides: 16